Computational Molecular Bioscience
Vol.3 No.2(2013), Article ID:32856,9 pages DOI:10.4236/cmb.2013.32003
Positional Information Storage in Sequence Patterns
1Fachbereich Mathematik und Informatik, Freie Universität Berlin, Berlin, Germany
2Department of Vertebrate Genomics, Max Planck Institute for Molecular Genetics, Berlin, Germany
3Biology Department, Center for Computational and Integrative Biology, Rutgers University, Camden, USA
4Institut für Medizinische Genetik und Humangenetik der Charité—Universitätsmedizin Berlin, Berlin, Germany
Email: *pdmitri@hotmail.com
Copyright © 2013 Alexey A. Shadrin et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received February 22, 2013; revised March 23, 2013; accepted March 30, 2013
Keywords: Information Theory; Sequence Pattern; Genetic Information Conservation; Typical Set
ABSTRACT
We build a model of storage of well-defined positional information in probabilistic sequence patterns. Once a pattern is defined, it is possible to judge the effect of any mutation in it. We show that the frequency of beneficial mutations can be high in general and the same mutation can be either advantageous or deleterious depending on the pattern’s context. The model allows to treat positional information as a physical quantity, formulate its conservation law and to model its continuous evolution in a whole genome, with meaningful applications of basic physical principles such as optimal efficiency and channel capacity. A plausible example of optimal solution analytically describes phase transitions-like behavior. The model shows that, in principle, it is possible to store error-free information on sequences with arbitrary low conservation. The described theoretical framework allows one to approach from novel general perspectives such long-standing paradoxes as excessive junk DNA in large genomes or the corresponding Gand C-values paradoxes. We also expect it to have an effect on a number of fundamental concepts in population genetics including the neutral theory, cost-of-selection dilemma, error catastrophe and others.
1. Introduction
Optimality principles such as Maupertuis’ or the least action and their different formulations and applications are the foundations of physics, but they are applied moderately in life sciences. Another field where the efficiency optimization is a quite practical problem is Information Theory (IT) [1], which received its first serious attention due to the tough efficiency demands in space flight communications [2]. Moreover even the relatively recent (1993) invention of “turbo codes” provided the breakthrough, doubling (!) the transmission efficiency. However, it is clear that the drive to optimality is central to biological systems as well—with other things being equal, more energy efficient species effectively have more resources available.
Information theory originally described the process of sending discrete data over noisy channel, which seemed to be quite similar to transmitting DNA sequences through generations with mutational errors. A few applications of IT in biology were attempted in order to exploit this similarity [3,4]. Nevertheless the engagement of IT in genetics is disappointingly limited, given the revolutionary role of IT in communications and the strong analogy between DNA sequence and discrete messages. As pointed by Eigen [5] the main challenge for such applications is how to quantify the biological value of a sequence. The value that counts is the transmission of a sequence (or a pattern, in our model) to next generations.
For “information” to have physical meaning it must be “relational”—in IT the information is defined as a degree of correlation between sender and receiver, and in the proposed model the correlation of 3D molecular shapes between interacting molecules signifies the amount of information, corresponding to the degree of specificity of interactions.
All molecular interactions can be viewed as more or less specific search (“homing”) for an interacting partner with subsequent “docking” and energy dissipation. And the most specific molecular interactions can likely be found in biological objects; for instance a “binding factor”—a protein (complex) which seeks and binds to a specific spot on DNA to regulate the corresponding gene expression. For the important IT-related reasons explained in the Methods section, many binging factors recognize not a single specific sequence but a large set of sequences, which has certain properties, forming the pattern for recognition. Here we present a theoretical model of evolution of such sets and corresponding patterns and provide some validating examples for real binding sites— we used abundant and well-annotated splicing sites of few mammalian genomes to support our conclusions.
Previous applications of IT in genetics were focused mainly on the problems of binding sites and factors operations in a genome. Von Hippel and Berg addressed the combinatorial and thermodynamic properties of binding, such as their specific recognition mechanisms [6] and applied statistical-mechanical concepts for affinity and binding dynamics [7]. Stormo focused on the problems of computational prediction and analysis of binding sites [8]. We, on the other hand, shift on the different level of abstraction and presume that the patterns for recognition are already established, and then we address a problem of what it takes to maintain such patterns through generations—how random mutations in patterns a redistributed between negative and advantageous, and the possibility to model total information dynamics of a gnome. Molecular evolution properties of binding sites were addressed in [9], however, there the classical adaptive evolution (i.e. through variants amplification and fixation) model was investigated. Another approach connecting genetic information with environmental information was undertaken by Frank [10] and was also based on classical adaptive evolution formalism. To our knowledge the problem of patterns maintenance, where a population acting as a “digital repeater” of stored information, without progressive evolution was not explored. The preservation of genetic information through pattern stability achieved by keeping allele frequencies constant was not suggested before and represented the novel concept in population genetics. While the formalisms for adaptive selection are quite developed and numerous, the formalism for “purifying” (maintenance) selection is practically absent—it is considered rather uninteresting—merely removing “negative” mutations. Besides other things, here we show that without the need for mutations amplification (fixation) the purifying selection in patterns may enjoy a significant fraction of beneficial mutations (significantly easing the need to remove negative mutations) and pattern composition can be adjusted to optimize mutation load under different circumstances.
We have to note that the problem of choice from a set, i.e. seeking for a site in a genome can be classified as a combinatorial problem rather than a full-featured IT application per se. The examples of core notions of IT, which paved its way to broad success, are the “channel capacity theorem”, “typical set” and ”asymptotic equipartition property” (in its basic version called ShannonMcMillan-Breiman theorem). To our knowledge neither of these concepts was applied in population genetics for the positional information, hence the present work is the attempt of more complete integration of IT conceptual framework into genetics models.
2. Methods
The genetic information can be viewed as positional in a general sense: it defines the process of homing and specific binding between molecules, including the binding of a molecule to itself, which is common for proteins and RNAs (i.e. secondary/tertiary structures). Hence such processes turn one-dimensional (sequential) DNA information into 3D shapes, and the energy inflow adds binding/unbinding kinetics, unfolding the temporal dimension. So we have all the basic “physical” properties for a living system: organized dynamic 3D structure with hereditary information stored on a molecular sequence.
The example of a binding site on DNA we widely used in this work, merely serves as a convenient visual illustration of the general phenomena. However, for instance the process of protein synthesis starting from transcripttion of DNA template can be viewed as a cascade of diverse homing, binding and unbinding events, hence the notion of positional information is quite universal.
Imagine an Engineer who wants to maintain positional information in a population of mutable replicating sequences. He can design recognizers (e.g. proteins— “binding factors”), which recognize specific sub-sequences (“binding sites”). For example to uniquely define the position on a (quasi-random) sequence of length L, he must use at least log2L bits of information, which takes half of this number of nucleotide positions to define, because each nucleotide position provides 2 bits. The possible number of unique binding sites is obviously . However, in this case any mutation in a site will break the recognition erasing the information. Hence the only possibility to maintain information is to avoid all mutations—if a mutation rate is sufficiently low and reproduction rate is high, then some of the progeny sequences will have no mutations and information can be maintained by discarding all mutated sequences–an extreme example of “purifying” selection. This (rather trivial) mode of maintenance can be accomplished only in small microbial genomes. However, what if mutations in binding sites in progeny cannot be avoided? In that case the Engineer must deploy “redundant coding” in terms of IT and to store information in redundant patterns—after a round of mutagenesis, at least some individuals will retain recognizable sequences and then selection retains only those individuals in a population, which keep the ensemble of patterns unchanged as a whole, in that case the information can be maintained indefinitely. Now a binding factor must recognize a set of (“synonymous”) sequences rather than a single sequence.
. However, in this case any mutation in a site will break the recognition erasing the information. Hence the only possibility to maintain information is to avoid all mutations—if a mutation rate is sufficiently low and reproduction rate is high, then some of the progeny sequences will have no mutations and information can be maintained by discarding all mutated sequences–an extreme example of “purifying” selection. This (rather trivial) mode of maintenance can be accomplished only in small microbial genomes. However, what if mutations in binding sites in progeny cannot be avoided? In that case the Engineer must deploy “redundant coding” in terms of IT and to store information in redundant patterns—after a round of mutagenesis, at least some individuals will retain recognizable sequences and then selection retains only those individuals in a population, which keep the ensemble of patterns unchanged as a whole, in that case the information can be maintained indefinitely. Now a binding factor must recognize a set of (“synonymous”) sequences rather than a single sequence.
Here we define “a site” as a specific site in a genome; “a (typical) set”—a set of functionally acceptable sequences for a site, which keeps its functional performance (a phenotype) within acceptable limits; “a pattern”— a set together with its equilibrium frequencies–some sequences in a set might be more frequent than others.
Here we are not concerned with specific ways of binding factors functioning or how selection picks individual sequences, for our goals it is sufficient to know the final result—the molecular “homeostasis” of patterns and corresponding sets. Apparently gene-specific binding sites of the same binding factor may have different acceptable sets, and/or equilibrium distributions within a set, depending on individual gene regulation requirements, hence their patterns should be regarded as different, though they are used by the same binding factor. These position-specific pattern differences are commonly neglected in the literature which applies computational methods involving genetic information (GI) formalism, because currently site-specific patterns are unattainable directly in normal populations due to insufficient divergence from the last shared ancestor of a site.
For the storage purposes alone the mutation rate can be pushed to a minimum. However, the evolvability demands non-zero rates, so the balance between information maintenance and evolvability is required. Here, for brevity, we focus mainly on the maintenance phenomenon, because a considerable change of the total genomic information can occur only on geologically large time scales (e.g. the human and chimpanzee genomes are ~ 99% identical), and once the maintenance mode is clarified, it is relatively clear how to model the progressive evolution of genetic information.
For simplicity we assume asexual population in equilibrium, constant population size, and a genome with the balanced content of four nucleotides. We also assume a pattern with independent positions, though more sophisticated “encoding” schemes can be evaluated, at this stage we prefer to keep things simple, because without the loss of generality the main predictions and conclusions of this model are sufficiently interesting for the suggested simple encoding scheme. Here we consider only single base substitutions, not exploring the roles of indels, genomic rearrangements, epigenetics, recombinetion, ploidy, variability or evolution of “recognizers”, etc. We consider the concise IT “engineering” problem as defined above. However, these things can be added as interesting extensions to the model without interfering with our conclusions drawn from the basic model.
We will use the term single position site or simply position (P), bearing in mind not a specific nucleotide, but a 4-vector (fA, fG, fC, fT), where each of fN, N Î {A,G,C,T} is a population frequency of corresponding nucleotide in a given position, as shown in Figure 1. Here by “population” we mean a set of sufficiently diverged sites, because in fact the sequences were taken from a single genome. However, in our engineering model of asexual equilibrium population the divergence will saturate and the population can be taken literally. Moreover, in the latter case we are able to correctly define site GIs, without the simplifying assumption “one binding factor—one pattern” which is necessarily taken in real populations. In order to examine patterns in actual genomes (which is not our goal here—we investigate the generalized model) one has to assume that position-specific patterns are sufficiently similar, i.e. the corresponding binding properties are sufficiently uniform, so that the pattern visualization in Figure 1 is essentially the average of (individually unobservable) exon-specific patterns, however, some exonspecific patterns’ differences are to be expected in reality. Figure 1 serves illustrative purposes for the pattern definition.
In equilibrium, when composition of a site does not affect phenotype, selection ignores it and the site contains no information by definition. Due to random mutagenesis this site in a population will be occupied by four nucleotides with equal frequencies of 1/4. However, if a site is functional, selection will affect equilibrium frequencies. The variability of a site can be naturally quantified by the entropy:
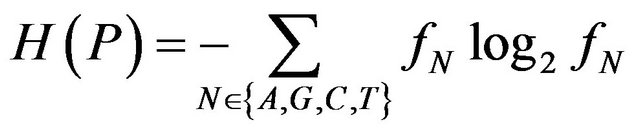 (1)
(1)
Non-functional site with frequencies of 1/4 has the maximum variability of 2 bits, and for a fully preserved site with single acceptable nucleotide the variability is zero. To obtain the measure of genetic information we have to take the reciprocal value: GI(P) = 2 – H(P). Correspondingly for a fully conserved site it takes the maxi-
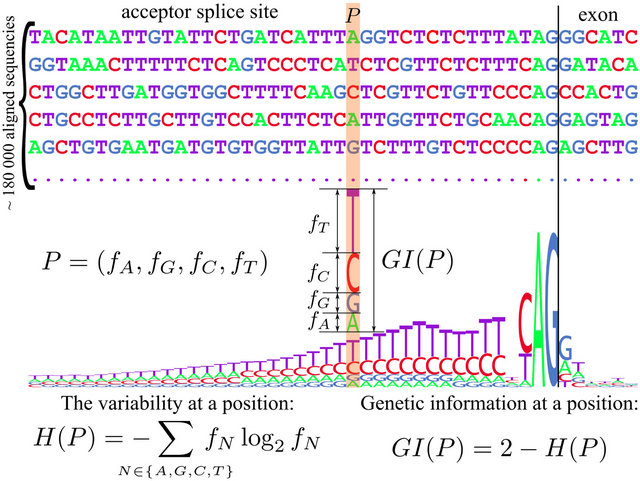
Figure 1. Definition of genetic information and sequence logo.
mum of 2 bits, for non-functional it is zero, while intermediate values quantify the degree of conservation, hence the biological value of this measure.
GI does not depend on permutations of elements in the nucleotide frequencies vector. Each GI value can be obtained with infinitely many variants of nucleotide frequency vectors, except for the degenerate cases of GI = 0 bit and GI = 2 bits.
This definition of GI was proposed more than 25 years ago by Schneider et al. [11] and has since become a standard tool for visualizing pattern composition called “sequence logo” [12] (Figure 1). Figure 1 shows the logo for a “spliceosome—a protein complex which recognizes the patterns of exons” “donor” and “acceptor” sites on pre-mRNA molecule and performs splicing of introns.
3. Results
3.1. Typical Sets and Positional Information
Schneider conjectured [13] and supported by simulations [14] that GI is additive and interpretable as localization (positional) information GIbinding = åGI(Pi), i.e., the sum of GIs of individual positions in a binding site is equal to the information necessary to locate it in corresponding sequence context. Hence the hypothesis is that besides the degree of conservation GIbinding has additional interpretation. Apparently the conjecture is interesting and biologically important but non-trivial because despite both values being “in bits”, the definitions of GI and localization information are different and not directly related. However, for sensible GI-modeling applications it is crucial to provide the rigorous proof of this conjecture.
If we describe an abstract binding site in terms of IT as a “source” which “generates” particular sequences (its realizations in a population), these two information values can be related with an aid of asymptotic equipartition property (AEP) [15]. AEP applied to our scheme effecttively states that a set of realizations of a binding site of length L and information GIbinding mostly fall into a “typical set” [16]. This means that while for non-degenerate GIs any sequence (out of possible 4L) can be an outcome, the ones actually observed, with probability close to 1 belong to the typical set having 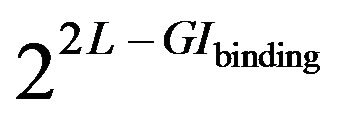 members distributed with approximately equal probabilities. The exponent value reflects the variability of a binding site, or a “source entropy”.
members distributed with approximately equal probabilities. The exponent value reflects the variability of a binding site, or a “source entropy”.
To select a single site from a sequence of length N the required information is log2N bits, interpretable as a number of binary yes/no questions required for the task. Less specific search requires less information: Selection of any item belonging to a set Nset requires log2N - log2Nset bits. Returning to the localization information we recall that a binding factor defines the corresponding typical set, recognizing sequences belonging to it and ignoring all others. Then it is easy to see that the corresponding localization information is equal to GIbinding. This result naturally links the continuous transversal variability (i.e. across population, orthogonal to multiple sequences alignment) with the discrete “longitudinal” localization on a sequence. The content of a typical set might provide a biological error protection mechanism: if a mutation does not remove a sequence from corresponding typical set, it is effectively “synonymous”.
To our knowledge the additivity of GI was not proved but was used as an ad-hoc conjecture, since it is impossible to prove it without proving AEP. However the additivity of GI is a critical property for whole-genome information modeling. Also a sequence “typicality” (as an object for selection force) concept may prove useful as it represents a binding site collective property, naturally accounting for single positions cumulative effects, as opposed to modeling of interaction of large number of separate selection coefficients for each allele in each position. Typicality considerations indicate that the same mutation can either make a site more typical or less typical, depending on the other site’s positions, hence the mutation selective value can be of different signs depending on the background.
3.2. Principle of Conservation of Genetic Information
By definition “population genetics is the study of allele frequency distribution and change” [17]. In classical models frequencies of alleles with unequal fitness are not stable. Such site will evolve either through fixating and carrying the most advantageous allele in whole population, or will be lost due to the pressure of negative selection, or “neutral” evolution with random fluctuations of frequencies before it will be either fixated or lost by chance. All these scenarios are transient. Despite the “homeostasis” notion being ubiquitous in living systems, in population genetics there are no terms or concepts for the description of evolution of weakly conserved sites (e.g. the “tail” of the pattern in Figure 1), where what matters is the stable bias of frequencies, rather than a fixation, neutrality or loss (which are the limiting cases for our model). Here, for brevity, we do not consider fitness of particular alleles altogether; all we are formally concerned with is GI value. Classically the selective value for a mutation is assigned somewhat ad hoc, and then its destiny in a population is traced with some mathematical model. In contradistinction once we define a pattern (or a whole-genome pattern set), the value of any mutation is also defined (through its contribution to sequence typicality). Hence the GI profile can be considered as the lowest level phenotype because higher level phenotypes are mechanistically derived from it. Then we have the opportunity to model whole-genome phenotype conservation without explicitly defining high-level phenotype.
Traditional models consider only two alleles due to common observations: the vast majority of observed variants (e.g. SNPs in a population) have two states, because too little time passed since the last common ancestor. However, for our model we ask what if this time goes to infinity in a stable population without progressive evolution and other disturbing events. When we understand the equilibrium we can explore the evolution of variability “snapshots” created by recurring population bottlenecks.
We suggest the law of GI conservation in population genetics–a position with any intermediate value of GI can be at equilibrium, maintaining constant GI and nucleotide frequencies (hence the pattern and positional information of the corresponding binding site). So-called “balancing selection” where the frequencies may be stable due to heterozygotes advantage [18,19] is apparently different from our generalization (possibly interesting ploidy effects are not explored here for brevity).
The information already accumulated in a genome requires maintenance to prevent mutational degradation and the majority of accumulating mutations (in functional sites) reflects the maintenance. Traditional models are often based on historical observational biases: for instance, it is easier to observe and study Mendelian traits as compared to low penetrance [20] effects. Other examples are the dramatic “selective sweeps” and “bottlenecks”, which we believe are spectacular but special evolutionary events, scrambling the mundane maintenance phenomena as populations variability collapses. However, these events per se contribute negligibly to the bulk of genetic information, which is in the maintenance mode. Due to these collapses the observed variability of a site in a population is typically much smaller than “potential” or “acceptable” variability which should be used to define the corresponding GI.
Forestalling, we can say that mutational expansion into this potential variability is perceived as the “neutral evolution” which in fact is the “maintenance evolution” where observed deleterious (for GI value) mutations are compensated by approximately equal amount of beneficial mutations. The role of beneficial mutations is usually overlooked in classical models, as common wisdom dictates that they are rare, so that all the maintenance is carried out by purifying selection, which is a special case in our model when GI is close to 2 bits.
3.3. Conservations of Splice Sites
The postulated constancy of frequencies and GI can be exemplified by the divergence of splice site patterns—the difference between mouse and human splice logos is quite small despite the large number of mutational and selective events happened since our divergence.
Maximum divergence of GI (less than 0.08 bit) can be observed in the fifth donor site position. Notably the number of splice sites is hundreds of thousands; hence mouse-human divergence shows the phenomenon of constant GI for the total of millions of nucleotide positions for a period of tens of millions of years.
As the average length of exons is ~100 nucleotides, splice sites constitute significant amount of genomic sequence in comparison with coding sequences; and it is natural to assume that this mode of evolution affects significant fraction of a genome besides splice sites. Other commonly known binding sites tend to be of sufficient length and high conservation (computational methods) and/or high binding affinity and specificity (experimental methods), creating observational biases with the preference for long sites with high GI per nucleotide. However, splice sites provide a unique opportunity for our analysis because of their large number and well-defined locations in a genome.
3.4. Mutational Load
By one of the classical definitions: “Genetic load is the reduction in selective value for a population compared to what the population would have if all individuals had the most favored genotype” [21]. Again this definition is for a site with GI = 2 bits, however, the load arising due to maintenance of a site with GI less than 2 bits should be defined differently.
Traditionally equilibrium states are modeled through their stability to perturbations, i.e. deviation from the equilibrium caused by some external perturbation is returned back by some stabilizing force. In our case the perturbations are random mutations and the force of (purifying) selection is compensating them. Thus it is straightforward to model the maintenance of a pattern: initially nucleotide frequencies are (fA, fG, fC, fT), then mutagenesis pushes them into (fa, fg, fc, ft), then these frequencies are corrected by reproduction and selection, preserving the initial value of GI and returning nucleotides frequencies back to the initial values:
 .
.
The changes in frequencies are assumed to be small.
Mutations can be of two types: transitions change a purine to another purine or pyrimidine to another pyrimidine: ti = {A « G, C « T} and transversions are all others: tv = {A, G « C, T}. Here we assume that all 4 transitions are equiprobable as well as all 8 transversions are. The system for descendant nucleotide frequencies can be written as:
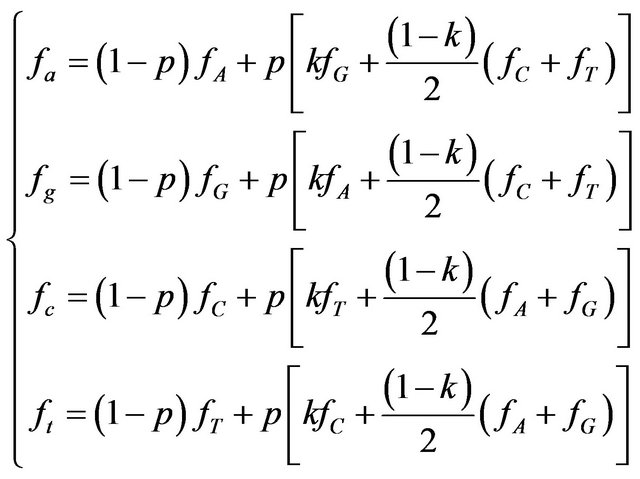 (2)
(2)
where p is mutation probability and k—probability of transition, upon condition that mutation occurred (k » 2/3 for mammals [22] corresponding to the ratio of transversions to transitions tv/ti = 1/2). Hence the deviation of frequencies due to mutagenesis is:
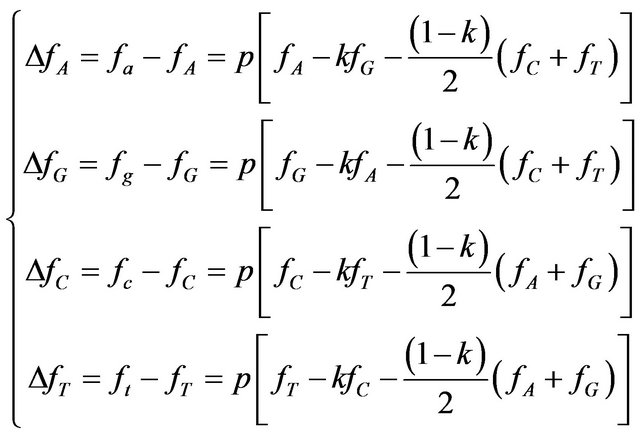 (3)
(3)
Due to the pressure of mutagenesis, the GI of descendant frequencies vector is always less or equal to initial GI (equality happens only if initial GI = 0 or p = 0).
As an example of one the many alternatives of optimization parameters we define a variant of mutational load (ML) as Manhattan norm of frequencies deviation vector:
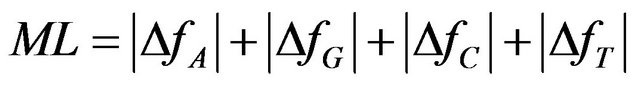 (4)
(4)
Minimizing this measure would minimize the number of mutations rejected by selection, minimizing the “genetic deaths” rate, making it biologically plausible. As can be seen from the expression for the optimal solution (see Equation (6)) in that case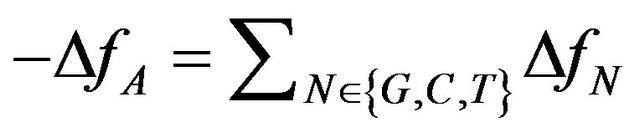 , and DfN ³ 0, " N Î {G, C, T}, assuming A to be the highest frequency variant. Then the selection can correct the frequencies simply by removing alleles (C, G and T) which increased in frequency. So the number of individuals which must go extinct is proportional to the defined ML which is equal to −2DfA for the optimal frequencies.
, and DfN ³ 0, " N Î {G, C, T}, assuming A to be the highest frequency variant. Then the selection can correct the frequencies simply by removing alleles (C, G and T) which increased in frequency. So the number of individuals which must go extinct is proportional to the defined ML which is equal to −2DfA for the optimal frequencies.
As we for simplicity consider equilibrium, we keep population size constant. Contrary to typical classical models, the population size does not matter for GI maintenance and evolution. Population size matters for phenomena such as selective sweeps—fixation of a suddenly appeared site with GI = 2 bits, which is a non-equilibrium event and out of the scope of this model.
With biased mutagenesis (k ¹ 1/3), different compositions (e.g. nucleotides permutations) of a 4-vector with the same GI can produce different ML (Figure 2). When two major nucleotides (Figure 2 left) are connected by transition, the impact of mutagenesis is largely compensated as the most probable mutations are transitions. Figure 2 right shows the opposite effect—non-compensated composition, where the major nucleotides “leak” strongly into the minor ones, hence causing larger ML.
The minimum ML for a given GI is the solution of the following optimization problem:
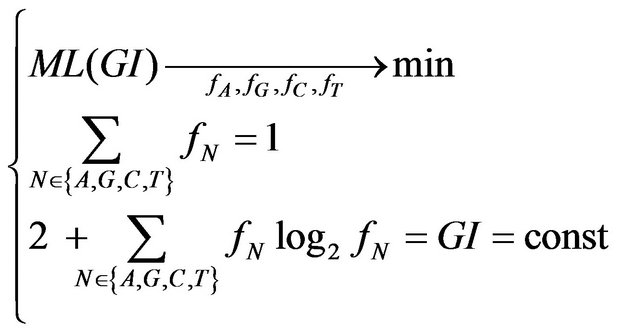 (5)
(5)
ML—mutational load which has to be minimized for a given GI value by adjusting the frequencies in 4-vector. The solution does not depend on the probability of mutation p, it was found numerically using evolutionary algorithm [23]. However, we also found its analytical representation, which in general case can be written in a parametric form (see Equation (6)).
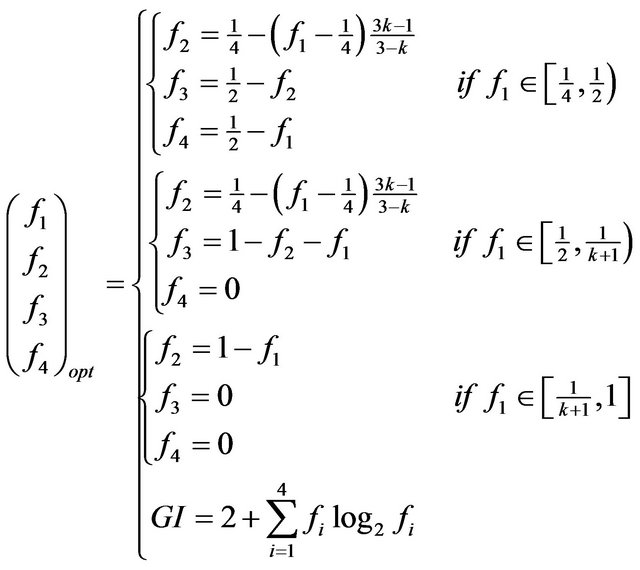 (6)
(6)
where f1 is the highest frequency, f2—the frequency connected to the f1 by transition, f3—maximum of transversions to f1, f4—transition to f3. k—probability of transition, upon condition that the mutation occurred.
The solution-the optimal frequencies vector vs. GI is shown in Figure 3. Optimal alleles’ sets (assignments of nucleotides to frequencies) are permutable. In the presence of mutational bias (k ¹ 1/3) top and bottom pairs of frequencies must be occupied by nucleotides connected through transition. In the case k = 1/3 (no mutational bias) all four frequencies are permutable with each other. The solution shows phenomenon resembling phase transitions-
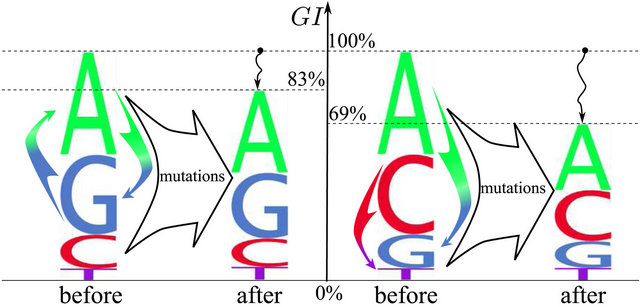
Figure 2. Changes of nucleotide frequencies and reduction of GI for different frequency vectors due to mutations with transitions prevalence. Only two most frequent mutations in a position are marked with colored arrows.
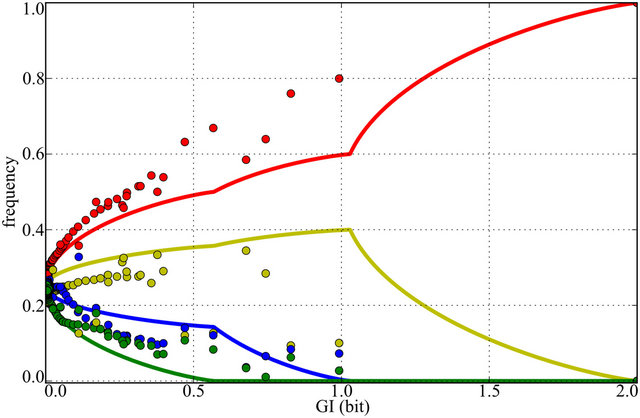
Figure 3. Nucleotide frequencies minimizing mutational load. Red line (f1)—the highest frequency nucleotide. Yellow line (f2)—the frequency of nucleotide, connected to the f1 by transition. Blue line (f3)—maximum frequency of the remaining nucleotides coupled through transition. Green line (f4)—transition to f3. Circles—frequencies of Homo sapiens donor and acceptor sites.
derivative discontinuities near 0.5 and 1 bits, with corresponding changes in the number of “degrees of freedom” and permutation symmetries. That is theoretically interesting because phase transitions are generally assumed to be highly non-analytic.
However, we cannot expect this experimental data to match this particular optimization precisely, because on the one hand other optimization parameters are possible (for instance a total site length to optimize the transcription speed), and the pattern (i.e. the logo) itself was derived with simplified assumptions outlined earlier (e.g. ignoring exons-specific individual patterns differences). Moreover it is natural to expect the existence of nonoptimal compositions due to specific regulatory demands.
3.5. Experimental Data
Using BioMart tools [24] we retrieved human exon coordinates and chromosome sequences from Ensembl database [25] and extracted acceptor and donor splice sites. Only the sites which obey so called GT-AG rule were kept in order to filter out the influence of minor spliceosome which may have different sequence pattern. As a result more than 180 thousands of each donor and acceptor splice site sequences were obtained. Corresponding nucleotide frequencies vectors and optimal frequencies bringing minimum to ML are presented in Figure 3. The trajectories of nucleotide frequencies in splice site positions are fairly consistent with the optimal—the top and bottom pairs of nucleotide frequencies are connected through transition, in 85% of positions with GI content higher than 0.05 bit.
We compared the substitution rates for splice sites divergence between human and two other primates—chimpanzee and rhesus (Figure 4). The conservation of the acceptor “tail” is quite weak: positions with GI < 0.4 bits have substitution rates higher than 80% of the neutral rate. However, the tail stores about 50% of positional information: ~5 bits as compared to ~10 bits of total acceptor information, 4 bits of which are provided by the “AG” site (Figure 1).
4. Discussion
Genes make up approximately 1.5% of human genome. Functional significance of remaining 98.5% non-coding DNA is still largely undetermined. A number of recent studies show that the signatures of purifying selection are wide-spread in non-coding DNA [27]. According to some estimates the fraction of functional non-coding DNA may 10 times exceed the amount of protein-coding sequences, reaching 15% of genome [28,29]. Such studies use sensitive techniques for detection of inter-species sequence conservation, compared to the neutral rate. However, it is difficult to find a significant amount of surely non-functional sequences with diverse context for precise calibration without numerous assumptions. We propose that weak patterns conservation is wider spread
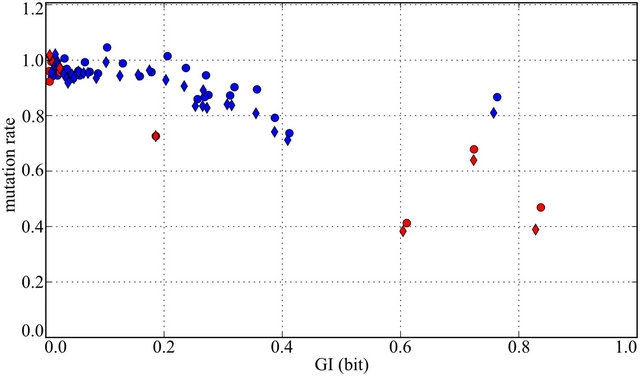
Figure 4. Normalized mutation rate of acceptor (blue) and donor (red) splice sites. Mutation rate was obtained using pairwise alignment of human vs. rhesus (diamonds) and human vs. chimp (circles) from the UCSC Genome Browser database [26] and then normalized to make mutation rate of positions with GI close to zero equal to 1.
than the above estimates (i.e. 15% of human genome), but the bulk of this functionality simply escapes detection by conventional methods. The provided model shows that it is possible to store any amount of error free (binding) information with arbitrary high substitution rates, provided sufficiently long sequences. This is analogous to the revelation in signal transmission theories occurred due to the understanding provided by IT: before the IT, the usable signal/noise ratio was supposed to be high and some transmission errors inevitable (e.g. the analog broadcast). However, the IT showed that with any noise level it was possible to perform efficient error-free communication. In genetics, the intuition that functional sequence must have high conservation (high signal/noise) went as far as calling weakly conserved sequences such as introns and intergenic non-repetitive sequence “junk DNA” (constituting about 50% of a genome), while we (keeping faith in nature’s thriftiness) speculate that it is the evolutionary innovation for increasing efficiency.
Another counter-intuitive feature of the proposed model is that significant fraction of random mutations is “positive”—compensatory for GI storage (Figure 2). For low GI about 50% of mutations are “good” (regardless of the vector optimality). This situation is unique to the positional information, as in classical Shannon’s setup all noise is “bad”.
The shift of paradigm we introduced here is to model the evolution and/or conservation of probabilistic patterns instead of evolution of defined sequences. A pattern can be thought of as a superposition of sequences (which forms the corresponding typical set). Instead of fixation as an elementary act of evolution, a mere shift in allele frequencies implies evolution in this framework. This seem to little sense for a single allele, however, for millions of alleles in a population, also considering that the frequency of beneficial mutations can be high, that introduces quite different mode of evolution than traditionally considered. For the first time this framework allows to model quantitatively the evolution of the total genomic information (due to additivity of GI), rather than modeling the fixation dynamics of single alleles with arbitrary assigned selective values. High frequency of beneficial mutations raises the question of what are the forces which impose the limits on progressive evolution, e.g. why some species are stable for millions of years.
A simple gedanken experiment with the provided model shows that for a given genome size, mutation and reproduction rates there is a limit on the amount of information which can be maintained in a population, so there is a limit on the absolute number of functional mutations a genome can tolerate, possibly explaining the Drake’s rule [30]. Hence we speculate that the IT notion of channel capacity, might provide some explanations for the limits of GI evolution, the drive to increase “coding efficiency” by deploying complex mechanisms of error corrections (e.g. DNA repair, ploidy, coding redundancy, nonsense mediated decay, etc.) and the utilization of weakly conserved sequences as an information carrier. Another “suspicious” fact worth mentioning is that presumably the most advanced species have the lowest known mutation rates even compared to close relatives among mammals.
With other things being equal, a species with better GI storage optimization (“coding efficiency”) is more efficient, since less genetic load effectively implies better survival rates. The “survival of the fittest” is equivalent to the survival of the most efficient, naturally including information processing efficiency. From IT, it is known that better efficiency requires higher complexity-coders and decoders must have memory and sufficient algorithmic complexity. In general approaching closer to the channel capacity limit requires increase of memory and computational complexity. Hence the IT naturally links the drive to efficiency with the drive to complexity. While the drive to efficiency is self-evident in biological systems the drive to complexity was difficult to rationalize. Traditionally, complexity is assumed to passively “emerge” as simple rules (interactions), applied recursively, can generate perceivably complex patterns (but still they are simple algorithmically), in contradistinction, the lesson from IT is that there can be an active drive to increase algorithmic complexity. From this perspective the “evolution” of IT itself is quite instructive [2]. As was mentioned, the IT had no general impact on scientific community before the limits were hit due to tough energy efficiency demands in space flight communications. These demands induced a boost of theoretical and practical developments, producing complex hardware and algorithms allowing approaching channel capacity limits and eventually bringing us the convenience of cellular and other digital communications. It is tempting to speculate that a similar evolution with the drive to complexity is happening on the “molecular machines” level.
5. Acknowledgements
We thank Anatoly Ruvinsky and Peter Krawitz for valuable comments and suggestions.
REFERENCES
- C. E. Shannon, “A Mathematical Theory of Communication,” Bell System Technical Journal, Vol. 27, No. 3, 1948, pp. 379-423, 623-656.
- O. Aftab, P. Cheung, A. Kim, S. Thakkar and N. Yeddanapudi, “Information Theory and the Digital Age,” 6.933—Final Paper, The Structure of Engineering Revolutions, Massachusetts Institute of Technology, Cambridge, 2001.
- H. Yockey, “Information Theory, Evolution, and the Origin of Life,” Cambridge University Press, New York, 2005. doi:10.1017/CBO9780511546433
- H. A. Johnson, “Information Theory in Biology after 18 Years,” Science, Vol. 168, No. 3939, 1970, pp. 1545-1550. doi:10.1126/science.168.3939.1545
- M. Eigen, “Selforganization of Matter and the Evolution of Biological Macromolecules,” Die Naturwissenschaften, Vol. 58, No. 10, 1971, pp. 465-523. doi:10.1007/BF00623322
- P. H. Von Hippel and O. G. Berg, “On the Specificity of DNA-Protein Interactions,” Proceedings of the National Academy of Science USA, Vol. 83, No. 6, 1986, pp. 1608- 1612. doi:10.1073/pnas.83.6.1608
- O. G. Berg and P. H. Von Hippel, “Selection of DNA Binding Sites by Regulatory Proteins. Statistical-Mechanical Theory and Application to Operators and Promoters,” Journal of Molecular Biology, Vol. 193, No. 4, 1987, pp. 723-750. doi:10.1016/0022-2836(87)90354-8
- G. D. Stormo, “DNA Binding Sites: Representation and Discovery,” Bioinformatics, Vol. 16, No. 1, 2000, pp. 16- 23. doi:10.1093/bioinformatics/16.1.16
- J. Berg, S. Willmann and M. Lässig, “Adaptive Evolution of Transcription Factor Binding Sites,” BMC Evolutionary Biology, Vol. 4, 2004, p. 42. doi:10.1186/1471-2148-4-42
- S. A. Frank, “Natural Selection. V. How to Read the Fundamental Equations of Evolutionary Change in Terms of Information Theory,” Journal of Molecular Evolution, Vol. 25, No. 12, 2000, pp. 2377-2396.
- T. D. Schneider, G. D. Stormo, L. Gold and A. Ehrenfeucht, “Information Content of Binding Sites on Nucleotide Sequences,” Journal of Molecular Biology, Vol. 188, No. 3, 1986, pp. 415-431. doi:10.1016/0022-2836(86)90165-8
- T. D. Schneider and R. M. Stephens, “Sequence Logos: a New Way to Display Consensus Sequences,” Nucleic Acids Research, Vol. 18, No. 20, 1990, pp. 6097-6100. doi:10.1093/nar/18.20.6097
- R. M. Stephens and T. D. Schneider, “Features of Spliceosome Evolution and Function Inferred from an Analysis of the Information at Human Splice Sites,” Journal of Molecular Biology, Vol. 228, No. 4, 1992, pp. 1124- 1136. doi:10.1016/0022-2836(92)90320-J
- T. D. Schneider, “Evolution of Biological Information,” Nucleic Acids Research, Vol. 28, No. 14, 2000, pp. 2794- 2799. doi:10.1093/nar/28.14.2794
- V. Girardin, “On the Different Extensions of the Ergodic Theorem of Information Theory,” In: R. Baeza-Yates, J. Glaz, H. Gzyl, J. Hüsler and J. L. Palacios, Eds, Recent Advances in Applied Probability, Springer, New York, 2005, pp. 163-179. doi:10.1007/0-387-23394-6_7
- T. M. Cover and J. A. Thomas, “Asymptotic Equipartition Property,” In: Elements of Information Theory, Second Edition, John Wiley & Sons, Inc., Hoboken, 2005, pp. 57-69. doi:10.1002/047174882X.ch3
- J. H. Postlethwait, “Modern Biology,” Holt, Rinehart and Winston, 2009.
- D. Charlesworth, “Balancing Selection and Its Effects on Sequences in Nearby Genome Regions,” PLoS Genetics, Vol. 2, No. 4, 2006, p. e64. doi:10.1371/journal.pgen.0020064
- H. Levene, “Genetic Equilibrium When More than One Ecological Niche Is Available,” The American Naturalist, Vol. 87, No. 836, 1953, pp. 331-333. doi:10.1086/281792
- R. Houlston, “Mutations: Penetrance,” General & Introductory Life Sciences, 2006, Online.
- J. F. Crow, “Some Possibilities for Measuring Selection Intensities in Man,” Human Biology, Vol. 30, No. 1, 1958, pp. 1-13.
- D. W. Collins and T. H. Jukes, “Rates of Transition and Transversion in Coding Sequences Since the HumanRodent Divergence,” Genomics, Vol. 20, No. 3, 1994, pp. 386-396. doi:10.1006/geno.1994.1192
- T. P. Runarsson and X. Yao, “Stochastic Ranking for Constrained Evolutionary Optimization,” IEEE Transactions on Evolutionary Computation, Vol. 4, No. 3, 2000, pp. 284-294. doi:10.1109/4235.873238
- S. Haider, B. Ballester, D. Smedley, J. Zhang, P. Rice, A. Kasprzyk, “BioMart Central Portal—Unified Access to Biological Data,” Nucleic Acids Research, Vol. 37, No. Web-Server, 2009, pp. W23-W27.
- P. Flicek, M. R. Amode, D. Barrell, K. Beal, S. Brent, Y. Chen, P. Clapham, G. Coates, S. Fairley, S. Fitzgerald, et al., “Ensembl 2011,” Nucleic Acids Research, Vol. 39, Suppl. 1, 2011, pp. D800-D806. doi:10.1093/nar/gkq1064
- P. A. Fujita, B. Rhead, A. S. Zweig, A. S. Hinrichs, D. Karolchik, M. S. Cline, M. Goldman, G. P. Barber, H. Clawson, A. Coelho, et al., “The UCSC Genome Browser Database: Update 2011,” Nucleic Acids Research, Vol. 39, Suppl. 1, 2011, pp. D876-D882. doi:10.1093/nar/gkq963
- M. Kamal, X. Xie and E. S. Lander, “A Large Family of Ancient Repeat Elements in the Human Genome is under Strong Selection,” Proceedings of the National Academy of Sciences USA, Vol. 103, No. 8, 2006, pp. 2740-2745. doi:10.1073/pnas.0511238103
- N. G. S. Smith, M. Brandström and H. Ellegren, “Evidence for Turnover of Functional Noncoding DNA in Mammalian Genome Evolution,” Genomics, Vol. 84, No. 5, 2004, pp. 806-813. doi:10.1016/j.ygeno.2004.07.012
- C. P. Ponting and R. C. Hardison, “What Fraction of the Human Genome is Functional?” Genome Research, Vol. 21, 2011, pp. 1769-1776. doi:10.1101/gr.116814.110
- P. Sniegowski, “Evolution: Constantly Avoiding Mutation,” Current Biology, Vol. 11, No. 22, 2001, pp. R929- R931. doi:10.1016/S0960-9822(01)00557-7
NOTES
*Corresponding author.

