American Journal of Analytical Chemistry
Vol.07 No.05(2016), Article ID:66272,13 pages
10.4236/ajac.2016.75039
Better Refined Adsorption Isotherm than BET Equation
Daekyoum Kim
Kwongmyoung-si Neobudae-ro, 32 Beon-kil, South Korea
Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/
Received 9 March 2016; accepted 3 May 2016; published 6 May 2016
ABSTRACT
During studying the heat capacity of metals and brightening more than the original
Keywords:
Refined BET, Binomial, Transforming, Adsorption Increasing Term, Surface Area, Inflection Point
1. Introduction
We derived the heat capacity equations of metals and then used consistent step multiplication of the appropriate binomial equations [1] . They are fitted to experimental data well [2] . The heat capacity equation (type V) and the adsorption equation (type II) draw sigmoid (S character) lines all together. And they are symmetrical with each other. The measurement gases of heat capacity are hydrogen and helium. The adsorption gases are vapor and nitrogen. The movements of their measurement gases are different. The formers are expansion and the later contraction.
The most important term in the derivation of heat capacity equation was the temperature increasing term,
. In case of adsorption it becomes
. Here 
and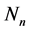 
are the total molecules adsorbed at the layers of 
and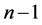
. Let us put 
which is unit in data fitting as the constant. The constant affects the adsorption equation from starting to ending like other constants. If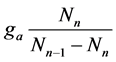 
is transformed into 
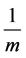power of 
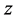in every derivation of adsorption such as 
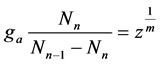[3] , the more advanced adsorption equation than BET eq. comes out. Hence we get the surface area.
2. Statistical Modeling of Adsorption Isotherm
Suppose each layer has one binomial equation. And suppose 
molecules are adsorbed on 
localized sites of the unit surface layers of the adsorbent and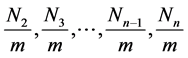 
molecules on 
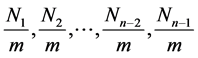sites made of 1st to 
layers in sequence. Here m is quantization constant. The first adsorption layer has 
adsorption energy and. the second to 
layers,
. Hence the adsorption probability on the first layer is 
and the non-adsorption probability
. Here 
is the adsorption constant of the first adsorption layer. 
is similar to 
in heat capacity equation. The adsorption constant, 
is calculable quantity. It is the expression to combine the rotation and vibration energy of the adsorbed molecules in the first layer. 
is similar to 
(Boltzmann’s constant) [2] . In the combination calculation of the first layer 
can take from 0 to 
as variables in sequence. Then the binomial equation of the first layer becomes [1]
(1)
Next the adsorption probability of from 
to 
layers is 
and the non- adsorption probability
. The binomial equations for from 
to 
layers are
(2)
Let us multiply Equation (1) and Equation (2) side by side. Then for
(3)
In the above 
(3.1)
In Equation (3) the largest term dominates the equation. So the total differential of Equation (3) becomes the zero which requires that the coefficients of all terms should be zero. Hence by using
. The first equation (Equation (1)) becomes
(4)
In [4] 
value should be corrected as those in the present figure (Figure 1). The constants have three parts of
. As we see in Figure 1, bonding constants mean quantization. If
, bonding occurs in many directions. If 
no quantization occur and if
, the adsorptions are interrupted in many directions. In Equation (4)
(4.1)
for 
(4.2)
It is possible that 
is put as unit.
Figure 1. Bonding constant and non-bonding constant in statistic quantization.
The next equations are
(5)
In Equations (4) and (5) let us put
, then 
which is same as Equation (9) of [5] solved by using the chemical potential
(6)
In Equation (6) add side by side and rearrange
(7)
In Equation (6) multiple side by side and rearrange
(8)
We solve Equation (8) with 
in order to eliminate 
(9)
We solve Equation (7) with Equation (9) in order to eliminate 
(10)
Equation (10) represents the adsorption amount of the first layer. It is Langmuir equation. The quantization values (
) and the numbers of the adsorption layer (
) are influential on the determination of
. All values of the parameters (
, 
, 
,
) directly participate in the determination of 
and following
. The
value of 
is much influential on the determination of the last term (
). But it does not much increase or decrease of 
since it exists in the denominator and nominator. At 
it becomes
(11)
Equation (11) is the same as Equation (10) obtained by using chemical potential in [1] . Therefore the total adsorption amount per unit surface (
), that is, the adsorption isotherm for from first layer to the last (
) layer becomes by using Equations (6) and (10) as follows
(12)
In the above
(12.1)
And the total adsorption rate is a linear function of 
made of four constants (
, 
, 
,
). The equation draws BET-like lines and fits BET type experimental data well. At 
it becomes
(13)
In the above
(13.1)
If the measurement gas is nitrogen, the general empirical formulae, 
is introduced into. 
to get the specific surface area of the adsorbate, 
[6] . Then 
is the mole-
cular weight of nitrogen and 
density of nitrogen and 
Avogadro number, Hence from empirical formulae 
=Å2/number is used. The monolayer capacity, 
should also be substituted by the value of the integration of Equation (12) subtracted by the surface adsorption isotherm (
).
3. Result and Discussion
The base of Equations ((10) and (12)) is
. So we may use the word, the rate without considering dimension. It affects the equation totally. Figure 2 shows the total adsorption rate according to the values of
. In accordance with the values of 
approaching units, the total adsorption rates approach closely with one another. This seems to mean that the adsorption heat of the first layer is same as those of 
layers. We call 
the quantization values. It seems to have same notion as the quantization appears in quantum mechanism. We are dealing statistical quantization which should exist in statistics. We can discern them, three cases. 
and
. The cases of 
and 
explain bonding and 
explains the existence of the interruptions for bonding. Figure 3 explains the increase of the adsorption rate according to 
values.
Figure 2. Theoretical adsorption isotherm curve, Equation (12) (m = 0.7, n = 4, ga = 0.5) with respect to βa values.
Figure 3. Theoretical adsorption isotherm curve, Equation (12) (n = 4, βa = 0.00901, ga = 1.0) with respect to m values.
Less 
than unit seem to interrupt the bonding. Figure 4 represents the total adsorption rates according to 
values. At less 
than 0.5 the isotherms show the same adsorption rates. The constant 
showed in Figure 5 should be positive. When 
and
, the constants draw the type II isotherm, but at 
the different type (type IV) of the isotherm appear. Figure 6 shows 
with respect to the relative pressure like Langmuir’s lines which can’t become unit even if 
is very large or 
much smaller. The parameter values of Figure 6 come from Figure 7 and Figure 8. According to the above variations we optimized two kinds of the experimental adsorption isotherm data showed in Figure 7 [6] and Figure 8 [7] using trial and error method. The experimental data of Figure 7 are obtained from the Figures 2-10 of [6] . The
Figure 4. Theoretical adsorption isotherm curves, Equation (12) (βa = 0.009, ga = 0.5, m = 0.7) with respect to n values.
Figure 5. Theoretical adsorption isotherm curve, Equation (12) (m = 1.7, n = 8, βa = 0.009) with respect to ga values.
Figure 6. Theoretical adsorption isotherm of the first layer using Equation (10) including experimental constants of Figure 7 and Figure 8.
Figure 7. Theoretical adsorption isotherm, Equation (12) (m = 0.9, n = 3.28, βa = 0.000011, ga = 1.0) with BET equation (c = 150) and experimental nitrogen adsorption at −196˚ on non-porous samples of silica and aluminna [6] .
experimental data are fitted to Equation (12) well. As we see in Figure 7 and Figure 8, BET isotherms there can’t imitate the experimental data except for beginning.
Equation (13) can be used in the data fitting with 
and
. Its quality is poor.
What is the catalyst? As we see Figure 9, 1, 2, 3, 4, 5, 6 and 7 molecules can function as the catalyst. That is, the molecules of the surface adsorption layer can’t function like the catalyst. Because they use much
Figure 8. Theoretical adsorption isotherm curve, Equation (12) (m = 2.4, n = 4.5, βa = 0.12, ga = 1.0) with BET equation (c = 130) curve and experimental water adsorption at 25˚ on cross-linked polystyrene sulfuric acid resin [7] .
Figure 9. Real adsorption molecules to get the surface area (numbered rings).
energy in order to hold the surface. So they are not active. The molecules which lie on the surface layer adsorption molecules which hold the surface, can function as the real catalyst. Therefore in Equation (12)
part must work in the adsorption reaction. Hence the real adsorption isotherm equation becomes
(14)
If this equation is integrated from the inflection point (
) to each relative pressure (
), we get the mono-area capacity (
) with respect to the relative pressure (
). Table 1 and Table 2 include those. Then
Table 1. 
(mono-area capacity) and 
(surface area) for Figure 7.
Table 2. 
(mono-area capacity) and 
(surface area) for Figure 8.
the surface area for the catalyst obtained from the equation becomes 
with 
per number for nitrogen and 
per number for water (Table 2.12) [6] by subs-
tituting
. in the equation of (2.60) of the reference [6] by 
in which 
= inflection point
and 
=optional 
value after the inflection point. In the above equation 
is the molecular weight (g) per g-mole and 
Avogadro number per g-mole.
Then the inflection points are obtained by Secant method [8] through the program showed in Appendix 1. Specific surface areas are changed according to the relative pressures. These are showed in Table 1 and Table 2 precisely. The integrations with respect to z values give the total adsorption site numbers of the adsorbate. Before the inflection point the specific surface area of the adsorbent is not counted as a catalyst since it makes the strong surface film [9] . The adsorption rate increases consistently after the inflection point. The values of 
of Figure 7 and Figure 8 match the range of the reference of BET [10] . The completion of 
goes with the completion of 
to the end as we see in Figure 6 and its equation. But from the inflection point the plugging of 
may begin characteristically.
We have felt intimately that the adsorption molecules of more than 2nd layers lie down the first layer molecules softly since the small quantity of adsorption molecules control the drawing and the surface area of numerical number.
Our study have realized the saying that “After considerable work on the theory, Hill (1946) formed the opinion that any future improvement on it must be in the form of refinement rather than a modification on the basic theory” [11] [12] .
4. Conclusion
The total adsorption rate equations closely related with the past references are derived correctly and the figures according to four constants (
) are also considered to describe BET-like figures (type II) well. The quantization constants are useful in deriving the adsorption equations. In order to calculate the surface area of the catalysts, the total adsorption equations excluding the first layer adsorption equation and their inflection points obtained are used appropriately. They fit the experimental data well.
Acknowledgements
The author thanks for the encouragements of Yongduk Kim, an emeritus professor of Sogang University.
Cite this paper
Daekyoum Kim, (2016) Better Refined Adsorption Isotherm than BET Equation. American Journal of Analytical Chemistry,07,421-433. doi: 10.4236/ajac.2016.75039
References
- 1. Reif, F. (1985) Fundamentals of Statistical and Thermal Physics. McGraw-Hill Inc Ed. 1965, Chapter 1, 10-46.
- 2. Kim, D., Lee, Y. and Kim, T.-W. (2010) Article Title. New Physics: Sae Mulli (The Korean Physical Society), 60, 729-740.
- 3. Mathews, J.H. and Howell, R.W. (2001) Complex Analysis for Mathematics and Engineering. 4th Edition, Jones and Bartlett Publishers, Inc., Section 2-3, 62-69.
- 4. Kim, D. (2000) Statistical Condensation Adsorption Isotherms of Gas Molecules Adsorbed on Porous Adsorbents, Surface Monolayer Adsorption Isotherms and Hysteresis Phenomena. Korean Journal of Chemical Engineering, 17, 600-612.
http://dx.doi.org/10.1007/BF02707174 - 5. Kim, D. and Choi, Y.S. (2011) Brightness of Lena’s Image for Various γ Values by Using Differentials of the Geometric Mean Heat Capacity Equations at Constant Volume. New Physics: Sae Mulli (The Korean Physical Society), 61, 248-255.
http://dx.doi.org/10.3938/NPSM.61.248 - 6. Gregg, S.J. and Sing, K.S.W. (1969) Adorption, Surface Area and Porosity. Academic Press Inc. (Ltd.), Chapter 2, 53, 77.
- 7. Sundheim, B.R., Waxman, M.H. and Gregor, H.P. (1953) J Phys Chem., 57, 974-978.
- 8. Ji, Y., Kim, H. and Heo, J. (2002) C-Roguhyouhan Numerical Analysis (Korean Language). Nopigipi Publishing Company, 24-27.
- 9. Jura, G. and Harkins, W.D. (1944) Surfaces of Solids. XI. Determination of the Decrease (π) of Free Surface Energy of a Solid by an Adsorbed Film. Journal of the American Chemical Society, 67, 1356-1362.
http://dx.doi.org/10.1021/ja01236a046 - 10. Brunauer, S., Emmett, P.H. and Teller, E. (1938) J. of Amer. Chem. Soc., 90, 309-319.
- 11. Caurie, M. (The Year after 1979) J. Food Sci.
- 12. Caurie, M. (The year after 1979) J. Food Sci., 63.
Appendix 1
/*--Finding zero by Secant method [8] to get inflection point from Eq. (12). with c++ and c languages */
#include
using namespace std;
#include
#include
#include
float eval_f(float x); //evaluation of f(x)
float fprime(float x1,float x2); //diff. of f(a)
void main()
{ float x1,x2,xn,e;
int i=0;
printf(“\nType initial point: “);
scanf(“%f”, &x1);
printf(“\nType second point: “);
scanf(“%f”,&x2);
printf(“\nType acceptable error interval in y: “);
scanf(“%f”, &e);
i=0;
do
{ xn=x1-eva;_f(x1)/fprime(x1,x2);
x1=x2;
x2=xn;
printf(“\n%3dth Iteration Root :%f
++i,xn,fabs(eval_f(xn)));
getch();
} while(fabs(eval_f(xn))> e);
}
float eval_f(float x)
{ float b;
//cout<<”x=”<
double bc;
double bb,bb1,bb2,cc,dd,dd1,dd2,dd3,ee,ee1,ee2,ff,ff1,ff2;
double aa,aa1,aa2,ba1,ba2,ba3,ccc1,ccc2,cc1,cc2,cc3,cc4,cc11,cc12;
const double b1=.000091,ga=.983,an=10.0,am=.64;
double ad21,ad22,ad23;
bb=pow(x,(1./am))-pow(x,(an/am));
bb1=(1./am)*pow(x,(1./am)-1.))-(an/am)*pow(x,(an/am-1.));
bb2=(1./am)*(1./am-1.)*pow(x,(1./am)-2.))-(an/am)*(an/am-1.)*pow(x,(an/am-2.));
ccc1=-(1./am)*pow(x,,1./am-1.);
ccc2=-(1./am)*(1./am-1.)*pow(x,1./am-2.);
cc1=pow((1.-pow(x,1./am)),-1.);
cc2=pow((1.-pow(x,1./am)),-2.);
cc3=pow((1.-pow(x,1./am)),-3.);
cc4=pow((1.-pow(x,1./am)),-4.);
dd=pow(x,(an/am))/ga;
dd1=(an/am)*pow(x,((an/am)-1.))/ga;
dd2=(an/am)*(an/am-1.)*pow(x,((an/am)-2.))/ga;
ee=pow(x,2./am)-pow(x,an/am);
ee1=(2./am)*pow(x,(2./am)-1.)-(an/am)*pow(x,(an/am)-1.);
ee2=((2./am)*(2./am-1.)*pow(x,(2./am)-2.)-(an/am)*(an/am-1.)*pow(x,(an/am-2.);
ff=((an-1.)/ga)*pow(x,an/am);
ff1=((an-1.)/ga)*(an/am)*pow(x,(an/am)-1.);
ff2=((an-1.)/ga)*(an/am)*(an/am-1.)*pow(x,(an/am)-2.);
aa=bb*cc1+dd;
aa1=bb1*cc1+(-1)*cc2*ccc1*bb+dd1
aa2=bb2*cc1+(-1)*cc2*ccc1*bb1+(-1)*(-2)*cc3*ccc1*ccc1*bb+(-1)*ccc2*cc2*bb+(-1)*bb1*cc2*ccc1+dd2;
ba1=pow((b1+aa),-1);
ba2=pow((b1+aa),-2);
ba3=pow((b1+aa),-3);
ad21=aa2*ba1+(-1)*ba2*aa1*aa1+(-1)*(-2)*ba3*aa1*aa1*aa+(-1)*aa2*ba2*aa+(-1)*aa1*aa1*ba2;
ad22=ee2*cc2*ba1+(-2)*cc3*ccc1*ee1*ba1+(-1)*ba2*aa1*ee*cc2+(-2)*(-3)*cc4*ccc1*ccc1*ee*ba1+(-2)*ccc2*cc2*ee*ba1+(-2)*ee1*cc3*ccc1*ba1+(-2)*(-1)*ba2*aa1*cc3*ccc1*ee+(-1)*(-2)*ba3*aa1*aa1*ee*cc2+(-1)*aa2*ba2*ee*cc2+(-1)*ee1*ba2*aa1*cc2+(-1)*(-2)*cc3*ccc1*ba2*aa1*ee1;
ad23=ff2*ba1+(-1)*ba2*aa1*ff1+(-1)*(-2)*ba3*aa1*aa1*ff+(-1)*aa2*ff*ba2+(-1)*ff1*ba2*aa1;
b=ad21+ad22+ad23;
return(b);
}
float fprime (float x1,float x2)
{ float b6;
b6=(eval_f(x2)-eval_f(x1))/(x2-x1);
return(b6);
}