ABSTRACT

We consider the modeling and simulation by means of multiwavelets on many patches. Our focus is on molecular surfaces which are represented in the form of Solvent Excluded Surfaces that are featured by smooth blendings between the constituting atoms. The wavelet bases are constructed on the unit square which maps bijectively onto the patches embedded in the space. The cavity which designates the surface bounding a molecular model is acquired from the nuclei coordinates and the Van-der-Waals radii. We use multi-wavelets for which the wavelet basis functions are organized hierarchically on several levels. Our assembly of the linear system is accomplished by using a hierarchical tree which enables the treatment of large molecules admitting thousands of patches. Along with the patch construction, some wavelet simulation outcomes which are applied to realistic patches are reported.

Keywords:

Wavelet, Patch, NURBS, Connolly, Modeling

1. Introduction

Boundary Element Method (BEM) has important applications in ion channels, pH computation, membrane simulations and synthetic medicines. Reduction of dimension is the principal advantage of BEM [1] over the traditional FEM (Finite Element Method) [2] [3] [4] [5] as a 3D problem is reduced to an equation located on a 2D- manifold. That enables the use of a 2D-surface embedded in the space instead of a massive 3D-mesh. That is particularly important in the case that one is only interested in the solution on the surface of a given geometry or in the infinite domain beyond the geometry as frequently occurring in quantum simulations [6] [7] . In addition, the convergence is substantially faster because only a small degree of freedom is sufficient to attain a precise approximation. This article treats the modeling and simulation using the wavelet Galerkin equation which is formulated on patched manifolds. This current implementation has an advantage of functioning in parallel on a multi-processor computer architecture that accelerates the computations considerably. A major drawback of BEM is that the matrix density requires a large memory capacity when the trial functions are standard polynomial bases whose pertaining linear system nece- ssitates a dense linear solver. Wavelets [8] [9] admit a significant advantage over the traditional polynomial bases because the wavelet technique compresses the BEM matrices efficiently [10] [11] . The surface structure which is required by the wavelet- BEM is unfortunately very complicated to construct in contrast to the standard mesh generation [12] . In the current paper, we consider a twofold objective related to modeling and simulation. First, we will describe the molecular surface generation when a set of atoms is provided. The resulting surface structure is suitable for the wavelet- BEM integral equation solver [13] . Afterward, we will apply a BEM simulation on the resulting models. This paper focuses on the practical aspect of the wavelet method for realistic data. The entire molecular surface needs to be decomposed into four-sided patches. One needs a parametrization which maps the unit square to each four-sided patch. The mapping has to be bijective, sufficiently differentiable with bounded Jacobian. Thus, the decomposition becomes conforming as non-matching curvilinear edges are not allowed. Some pointwise agreement for adjacent mappings is therefore fulfilled. That enables the construction of multi-wavelets which are understood in the sense that the wavelet bases are structured on hierarchical levels [14] . Before pro- ceeding further, we survey some related works in the past. The technique which provides a splitting method for CAD surfaces is proposed in [15] where methods for checking regularity of Coons maps is additionally proved. The main task in [16] is the correlation between the transfinite interpolation [17] which resides in an individual patch and the global continuity. While approximations are required to obtain global continuity in [16] for CAD objects, it can be achieved exactly for molecular surfaces in [18] . That is due to the fact that both circular arcs and spherical patches [19] can be exactly recast as NURBS (Non-Uniform Rational B-Spline) [20] . Furthermore, a real chemical simulation by using wavelet BEM is employed in [7] for the quantum computation. A wavelet BEM simulation using domain decomposition techniques was described in [21] which treats the case of ASM (Additive Schwarz Method). It was utilized as an efficient preconditioner for the wavelet single layer potential which is badly conditioned. Recently, we gained experience [3] in elasticity nanosimulation where one has used nanotube fibers immersed in polymer matrices as quantum models. The organization of this current paper is structured as follows. First, it starts by describing the essential steps for constructing the smooth patch decomposition. We proceed afterwards to the presentation of a hierarchical tree method to compute the wavelet integrals when coupled with the Genz-Malik approach [22] [23] . The matrix entries are usually integrals with 4D integrands which are singular. Toward the end, we present some results pertaining to the patch decomposition in which the inputs are either water clusters obtained from former molecular dynamic simulations or quantum models obtained from PDB (Protein Data Bank) files. In addition, we report on BEM results including the execution runtimes for the different stages in the BEM simulation. Further, we will briefly display the acceleration of the executions when utilizing computers admitting a multi-processor architecture.

2. Integral Equation on Molecular Surfaces

Our modeling and simulation are performed on a cavity [24] which is acquired from the boundary of molecules where each constituting atom is represented as an imaginary sphere whose center 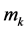corresponds to the nuclear coordinates and whose radius to a scaled Van-der-Waals radius of the atom. That is, by denoting the sphere of center 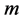and radius 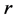by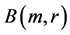, the molecule is represented as the union of spheres. We need additionally a probe atom which serves as smoothing of the molecular surface. The SES (Surface Excluded Surface) model [25] which is also known as Connolly surface [26] is the surface 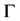traced by the probe atom when it is rolled over (see Figure 1) the whole surface. The Conno- lly surface is extracted partly from and partly from the blending surfaces traced by the probe atom. The blending surfaces are composed of surfaces of two types. The first type consists of toroidal surfaces while the second one of trimmed spherical surfaces. Our first objective is to decompose the Connolly surface into 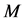four-sided patches [18] admitting (see Figure 2(a)) the following properties:

• We have a covering of the molecular surface by patches,

• Each patch where is the image by which is described by a bivariate NURBS function that is bijective, sufficiently smooth and admitting bounded Jacobians,

• The intersection of two different patches and is supposed to be either empty, a common curvilinear edge or a common vertex,

• The patch decomposition has a global continuity: for each pair of patches, sharing a curvilinear edge, the parametric representation is subject to a matching condition. That is, a bijective affine mapping exists such that for all on the common curvilinear edge, one has. In other words, the images of the NURBS functions and agree pointwise at common edges after some reorientation,

• The manifold is orientable and the normal vector is consistently pointing outward for any

For each patch, the Gram determinant is denoted

(1)

The space of square integrable functions is

(2)

which is equipped with the following scalar product and norm after transformation onto,

(3)

The Sobolev space on for a non-negative integer is

(4)

where the differentiation is interpreted in the sense of distribution [27] such that for all compactly supported smooth functions. The Sobolev space is endowed with the norm

(5)

Concerning a real positive order such that is an integer and, the Sobolev space consists of the functions such that their norms with respect to the next Slobodeckij norm are finite

(6)

For negative orders, one employs the dual spaces. By desig- nating the region enclosed within by, our second objective is to solve the interior problem:

(7)

Introduce the double layer operator

(8)

(9)

In the general case, we have the following mapping using Sobolev spaces

(10)

which is linear and continuous. In the current case, since the entire molecular surface is sufficiently smooth, we have

(11)

for any real number according to Theorem 7.1 and Theorem 7.2 of [28] . In particular, we deduce the bounded linearity with respect to square-integrable functions:

(12)

We make now the change of unknown

(13)

by using as the new unknown which is also termed as density function. As a point approaches, we have [28] [29] [30]

(14)

because the manifold contains neither a nonsmooth edge nor a sharp corner. The function as mentioned in (13) is harmonic in the sense that. Therefore, in the case that satisfies

(15)

then on account of (14), the function solves the boundary value problem in (7). In operator form, we have the next integral equation after multiplication by (−2):

(16)

By discretizing (16) in some finite dimensional space, one searches for such that for all

(17)

where we use the kernel

(18)

The subspace will be piecewise polynomials which could be piecewise constant so that we have in particular. Once the solution to the integral Equation (16) becomes available, the solution to the initial boundary value problem (7) is recovered by applying (13). Since both the wavelet basis function and the mappings are expressed in term of B-spline basis, we shall recall briefly some important properties of a B-spline setting which represents piecewise polynomials. Consider two integers such that. Should the interval be the domain of definition of the B-spline, that interval is subdivided by a knot sequence such that for and such that the initial and the final entries of the knot sequence are clamped and . One defines the B-splines [31] [32] [33] basis functions as

where one employs the divided difference in which one uses the truncated power functions given by if, while it is zero otherwise. The integer controls the polynomial degree of the B-spline which admits an overall smoothness of where the case corresponds to discontinuous piecewise constant functions needed for the Haar wavelet. The integer controls the number of B-spline functions for which each B-spline basis is supported by. The NURBS patch admitting the control points and weights is expressed as

(19)

As for the construction of the finite dimensional space, since the Gram determinant is bounded

(20)

the above structure of the surface allows to construct bases on 2D which are carried over the manifold that is embedded in. The Galerkin variational formulation with respect to a finite dimensional space spanned by uses the approximating functions where are the BEM- unknowns. The next linear system is eventually obtained

(21)

such that the matrix entries and the right hand side are

(22)

(23)

(24)

In general, the linear system (21) is troublesome because the basis functions yield a dense matrix for the operator. In term of memory, if are standard

polynomial basis functions, the matrix requires storage to accommodate all entries. In addition, the determination of a matrix entry of calculates an integration in where the integrand is highly nonlinear and possibly singular depending on the patch pair. By using tensor product B-spline wavelet basis functions, the matrix becomes quasi-sparse. For the instance of high-order odd wavelets [34] [35] , we depict on Figure 2(b) the quasi-sparse matrix entries for a 2D singular operator where very small entries are set to zero.

3. Patch Generation for Wavelet Bases

Let us specify the assumptions concerning the positions of the nuclei and the properties of the radii with respect to the probe radius. For every two arbitrary atoms and, we assume that one of the following two conditions holds.

(C1) Either the two enlarged spheres and by the probe radius are completely disjoint such as,

(C2) or we have and additionally

Those two assumptions exclude the situation where the blending torus which is tangent to both and admits a self-intersection. If assumptions (C1) and (C2) are not fulfilled but one still wants to treat the molecule, one carefully inserts additional dummy atoms between every two atoms and for which there is a toroidal self-intersection. The sizes and the positions of the dummy atoms should be minimized while keeping the shape of the initial molecule. We will consider the generation of the constituents of the B-Rep (boundary representation) of the SES surfaces. For two spheres and, we define their power distance as. The -th Laguerre cell is com- posed of points which are closer to than to any other with respect to the power distance:. A Laguerre decomposition of with respect to the spheres is. If all radii are equal, the Laguerre decomposition coincides with the usual Voronoi decomposition as illustrated in Figure 3(a). For two spheres and, the radical axis is the set of points which are equidistant to and with respect to the power distance. Such a set is a plane given by

The Laguerre cell is a convex polyhedron which has faces from the radical axes and which could be bounded or unbounded. To obtain the Laguerre decomposition, we consider the uplifting function which associates to the value . After generating the convex hull of the set of four dimensional points, the projection of the lower face of on the space generates a weighted Delaunay tetrahedral decomposition [36] having apices. Each apex of the Laguerre cell is the orthocenter of a tetrahedron of the weighted Delaunay. The Laguerre decomposition is obtained by the dual of the weighted Delaunay. We describe next the way of obtaining the spherical trimmed surfaces of each atom by considering its cell. For each neighboring cell of, consider the cell planar face which separates the spheres and. One generates two offset planes and by orthogonally shifting by and toward those two spheres respec- tively. Two circles and are traced on those spheres by and. We discard the circular arcs on which are either included inside an atom other than or between the planes,. By organizing the remaining circular arcs, we obtain several closed curves on the sphere. These bounding curves yield several spherical trimmed surfaces on the sphere. Each face of the Laguerre decomposition corresponds to one torus which is tangent upon and. To obtain the toroidal surface, we trim off the toroidal part of which is beyond the parallel planes,. If the rolling probe atom touches at least three atoms, we construct a spherical blend whose boundary is composed of the arcs which are the intersections of the toroidal surface and the probe atom. At this point, we have subsurfaces which are bounded by some circular arcs. Stereographic projections serve as parametrizations of the subsurfaces from some trimmed planar domains. We describe now the decomposition of a Connolly surface into large four-sided subsurfaces. We use a triangular mesh of the whole surface as an intermediate step. We determine first the underlying structure of a coarse quadrangulation. We deduce the nodes, edges and quadrilaterals of from the mesh. We start from a fine quadrangulation which is obtained by subdividing each triangular element of into three quadrilaterals. The resulting quadrangulation is not directly useful for patch representation because it is too fine. As a consequence, we need to coarsen that fine quadrangulation repeatedly in which we initialize. Each coarsening step from to consists in amalgamating a few neighboring quadrilaterals in the quadrangulation to form a coarser local simplified quadrangulation in. It is a long programming to implement many local patterns of simplification and to recursively determine the parts of to coarsen so that the final patches have similar surface areas. Since the initial finest quadrangulation is inappropriate to be used as, we impose minimal and maximal numbers of coarse quadrilaterals. For the recursive quadrangulation simplification, we use a coarsening parameter which gauges the density of. A unit value of corresponds to the finest allowed quadrilateral decomposition while a value of approaching zero corresponds to a very coarse quadrilateral decomposition. After assembling having straight edges, we need to connect every two nodes and on the endpoints of every edge by a curve on the manifold as illustrated in Figure 3(b). That curve is described by means of a geodesic curve on joining to. First, we need a curve which traverses only the nodes and the edges of. Afterward, we improve that curve by allowing it to traverse the internal parts of the triangles of. Assembling the complete node-edge graph of the whole mesh is very memory consuming. Searching for shortest paths becomes very cumbersome for such a large discrete manifold. Some efficient data structure to accelerate the search is necessary in the implementation. We eventually fit each four-sided submeshes by NURBS patches where each interface curve has a matching parametrization by its incident patches. During the application of those geometric operations, tests must be performed in order to avoid manifold folding and tiny gaps. Many tests related to edge degeneration and angular quality are needed to be applied in practice.

In order to ensure the validity of conditions (C1) and (C2), one adopts the method of GEPOL in which some additional spheres are inserted [37] [38] . Those incorporated extra-spheres are not physically relevant. These are fictive spheres admitting neither atomic masses nor electric charges. The principal objective of the previously mentioned conditions is to avoid the conflicting situation where some toroidal blending surfaces occur when the corresponding two disjoint atoms are distant from one another so that the contact with the probe atom is almost tangential. In such a case, a self-intersecting toroidal blend is formed. In order to remedy that problem, a fictive non-atom centered sphere is inserted between every two atoms where those conditions are violated. It is worth noting anyhow that such a situation occurs only in very rare cases. We would like to explain the similarity and the difference between the above two types of smoothing surfaces which are the toroidal ones and the spherical ones. Both surfaces serve as blending surfaces between neighboring atoms. The principal difference between them is that the toroidal ones occur when only two atoms are touched by the probe atom, whereas a spherical blend appears when more than two atoms simulta- neously have contact with the probe atom as illustrated in Figure 1(a) and Figure 1(b). In the latter case, the number of atoms which touch the probe atom is three in most practical cases but that number can theoretically be arbitrarily many depending on the positions and the radii of the constituting atoms.

Now that we have a four-sided decomposition, we want to construct the wavelet spaces on the surface. Since every two incident patches admit pointwise joints, constructing the wavelet bases on the unit square is sufficient to construct basis functions on the whole molecular surface. Each -wavelet basis (see Figure 4(a)) will be constructed as a linear combination of B-splines

(25)

On level, we define a knot sequence such that and for and that the remaining. The internal knots on

the next level are obtained by inserting one new knot inside two consecutive knots on the lower level. Introduce the B-spline linear space on level:

(26)

By using the piecewise polynomial property of the B-splines and the inclusion, the B-spline bases form a nested sequence of subspaces:

(27)

As a consequence, the space can be expressed as an orthogonal sum

(28)

with respect to the -scalar product where is the wavelet space

(29)

By applying the decomposition (28) recursively, one obtains on the maximal level

(30)

The -wavelet spaces (see Figure 4(b)) on the unit square is defined for any maximal level as follows.

(31)

such that

We want now to survey the determination of the wavelet bases of. The construction of the higher-order wavelets [34] [35] requires the case on the whole infinite real line on which one has knot entries on each integer as. The cardinal B-spline is given by

(32)

which verifies the two scale relation

(33)

For the polynomial degree, the corresponding complementary space is spanned by the shifts of the wavelet function

(34)

Representing the derivatives in function of B-splines can be used to express the function in term of control points. The cardinal wavelets are orthogonal to B-splines on the infinite real line having integers as knot sequence. The cardinal splines serve as construction of internal wavelets on the interval by scaling and shifting. Only the odd wavelets for odd polynomial degree is described because the even case is defined almost similarly with the exception of additional central wavelets. One defines on level the clamped knot sequence, and where. The dependence on is sometimes dropped to simplify the notations. The -wavelets use the following internal knot sequence

(35)

The internal wavelet functions are defined by means of scaled and dilated transformations

(36)

Additionally, one needs boundary wavelet functions which are of the form

(37)

where the coefficients for the last summation are the control points of the cardinal wavelet. the control points of the cardinal wavelet. The remaining unknown coefficients on the first summation are obtained by solving

(38)

or. That ensures the -orthogonality

(39)

The previous construction creates wavelet basis functions. To complete the construction, the remaining ones are deduced by symmetry such as for,. The construction of the Haar wavelets and piecewise linear wavelets is very similar. The former corresponds to piecewise constant polynomials while the latter to piecewise polynomials of degree unity. Since every polynomial of degree can be expressed in term of, we obtain from the orthogonality (39) the property of vanishing moments:

(40)

for any fixed. It is an important property because it yields quasi-sparse structure of the matrix. By using the constructed wavelet basis, we are interested in the values

(41)

(42)

We will drop the indices of since we consider the integrals in the above summation for a fixed pair. By fixing some and by considering any, the Taylor expansion yields

(43)

(44)

For the first summation, by multiplication with a tensor product wavelet basis and by taking the integration over, one obtains for and where and

(45)

which is zero due to the property of the vanishing moment (40). As for the second summation, introduce for . The summation is estimated by . By defining , one obtains

(46)

Due to boundedness (20), one obtains for and on account of the Calderon-Zygmund inequality in the case:

(47)

which is small if the images and are sufficiently distant from one another. Thus, the speed of the decay toward zero depends on the factor using the vanishing moments exponent and the distances between the basis supports. Hence, the constructed wavelet basis has the advantage that it renders the operator quasi-sparse.

4. Wavelet Hierarchy and Integration

This section is occupied by the efficient computation of the matrix entries from (41). Since our method is based on a hierarchical tree on the B-spline knots, we describe next the procedure of inserting new knots into existing ones. The principal objective is to be able to efficiently express a function defined on the coarse knot sequence in term of B-splines on a fine one. Consider two knot sequences and such that. For both knot sequences, the smoothness index is conserved intact. One introduces

where. The discrete B-splines are defined as

(48)

which enables to express the basis in lower level in term of those in higher level such as

The De-Boor algorithm for the evaluation of the discrete B-splines utilizes the recurrence

in which for while otherwise. We will write interchangeably. In addition, for a knot entry on level, we denote by the index on level such that

(49)

Since one inserts one -knot entry between two consecutive -knot entries, one has in particular

(50)

We introduce the the following 4D-voxels

(51)

We will use the next multi-indices for the wavelet and B-spline bases

(52)

Since the tensor product wavelet bases verify

(53)

it suffices to compute

For the Haar wavelets where the corresponding B-spline are piecewise constant, we have four recurrences:

(54)

(55)

(56)

For wavelets admitting higher polynomial degrees, by using the discrete B-splines one also obtains four recurrences including:

Our objective is to avoid computing any involved integrals several times. Therefore, we construct a hierarchical tree whose nodes correspond to the 4D-voxels. We define the depth of the multilevel having 4D-indices to be. Each tree-node has offsprings

. By using the above recurrences, one traverses the hierarchical tree bottom-up in order to obtain the integrals on all relevant 4D-voxels. Thus, the wavelet integrals are computed hierarchically without doing any repeated computations. That is, one starts from the voxels having the largest depth. The worst case of the depth of the hierarchical tree is depending on the wavelet indices chosen in the quasi-sparse structure. For the current paper, we use the Genz-Malik integration [22] to compute the integrals corresponding to the leaves of the hierarchical tree. In a forthcoming paper, we will present a more efficient method for computing the leaf integrals. The integration on the voxels

are computed by transforming it onto. The Genz-Malik method evaluates the integral of a multivariate func- tion by utilizing the -point rule

The nonzero entry (resp. entries) of is (resp.) at the -th position (resp. -th and -th positions). In the cases, every application of requires 57 function evaluations. For the determination of the parameters in, one solves a nonlinear system [22] involving the functions

The solution to that nonlinear system gives exactly, , while the weights are, , , , . That integrator is combined with some adaptive subdivision in which -dimensional hypercubes that produce large integration errors are split into smaller ones. That subdivision starts from as the initial hypercube. During the recursive subdivision, the hypercubes to be split have to be identified. In order to evaluate the local error inside a hypercube, an error estimator is achieved by the next 5-point rule

where the weights are, , ,. In order not to evaluate the integrand too many times, the integration points for are taken from the 7-point rule. The error estimator is the difference between and. As input, one accepts the maximal number of integrand evaluations together with the desired accuracy. We apply the above numerical quadrature to in which we avoid zero division by replacing the kernel involving by for, where is an adjustable small parameter. A similar approach using has been used in [39] for the purpose of quantum mechanics using high-dimensional approximation.

5. Wavelet Simulation on Molecular Models

We want now to present some results of the former method which was implemented in C functions together with C++ classes. The visualization has been implemented with the help of OpenGL. The computations have been executed on a computer possessing a 4.1 GHz processor and 32 GB RAM. The C-packet cubature [23] serves as computation of the Genz-Malik integrations. We employ different sorts of quantum models including water clusters which are obtained from a former MD (Molecular Dynamics) simulation. A water cluster is generally a collection of many water molecules which take their positions after a Molecular Dynamic simulation. Each water molecule is interpreted as one single particle during the Molecular Dynamic steps. When the MD energy becomes stable as the sum of the kinetic energy and the potential energy is supposed to be conserved, the water molecules form a cluster from which a few particles that are located within a prescribed large sphere are extracted at equilibrium state. The hydrogen and oxygen atoms contained in that large sphere constitute the components of the water clusters. As a consequence, the water cluster forms in general a Connolly surface which takes the shape of a large ball. The radius of the given large ball controls the final size of the water cluster. Besides, we use also other molecules which are acquired from PDB files.

We would like to provide some numerical results pertaining to the runtimes of the cavity generation and the quality of the patches. The runtimes depend on several factors. First, it is affected by the number of atoms in the molecule. Second, it varies in relation with the atom distributions. Further, it depends on how coarse the patch decomposition should be. As a first numerical test, we investigate the number of patches in accordance to the size of the molecule. The results of such a test are gathered in Table 1 where we examine the coarsening from Section 3. According to our experience, the interesting practical values of range between 0.2 and 0.4. A smaller value of indicates that one has a coarser decomposition which amounts also to a fewer number of fitting tasks. On the other hand, a single large NURBS surface area needs many sampling points which mean also that it takes more time to complete the NURBS determination. Hence, the running time depends not only on the initial mole-

cular size but also on the surface area of the cavity. For example, lecithin has more atoms than DNA but the latter takes almost four times longer than the former.

The purpose of the second test is the investigation of the area of each patch. We would like to compare the areas of the patches in two perspectives: in the vicinity of each patch and global comparison. For the vicinity test, let denote the set of neighboring patches which share at least one corner node with a patch. We

computed where. The results for

the average values of are collected in the third column of Table 2 where we observe that the sizes of the patches vary slowly because approximates averagely the unity. As for the global comparison, the ideal patch area is the area of the whole molecular surface divided by the number of patches. We compute the ratio. The resulting average values of are exhibited in the last column of Table 2. We observe that the sizes of the patches are not too different from the ideal size. In fact, we have in general . Those patch properties enable the subsequent wavelet bases to be proportionally distributed. An instance of the patch decomposition for the case of a DNA section is depicted on Figure 5.

We focus now on investigating the patch quality which is quantified as follows for a patch on level. For each, we consider the quadrilateral having vertices, , ,. By inserting a diagonal in, one defines two triangles and. Two other triangles and are defined by inserting the diagonal. The quality metric

is used where is the smallest angle in the triangle. The ideal quadrilateral which is a perfect square corresponds to. In Table 3, we gather the results of our test which consists in computing the average values of over the whole patches. We obtain a satisfactory quality because the average values of do not tend to zero. We would like now to describe some results related to BEM simulation on realistic molecular patches. For the computer implementation, we use only Haar wavelets but the former method can also be applied to higher-order wavelets. We examine first the error reductions in term of the multiscale level for large molecules. The results are collected in Table 4 which contains both the absolute errors and the relative errors. The

models consist of a water cluster and a DNA section which admit respectively 1109patches and 2119 patches. We consider two exact solutions which are respectively and that have vanishing Laplacian. The right hand side is the restriction of the function on the boundary. The error reduction is affected by the exact solutions but in general the errors reduce satisfactorily in function of the wavelet levels. The absolute errors are obtained by comparing with the exact solution at some fixed samples in the interior. A division by the largest value of the exact solution provides the relative error.

We exhibit in Table 5 the runtimes for the different stages which are required for a complete BEM simulation. These include: (1) the assembly of the identity operator, (2) the determination of the indices which yield quasi-sparse matrix entries, (3) the computation of the singular integrals in the operator, (4) the solving of the resulting linear system. In addition, Table 5 exhibits the required total runtimes for two water clusters which contain respectively 386 patches and 1109 patches on several multiscale levels. It turns out that the construction of the identity operator executes very quickly. The task which mainly dominates the BEM-simulation is the assembly of the singular operator. Although the determination of the quasi-sparse indices and the solving of the linear system take some time, they do not last as long as the singular operator. A GMRes method serves as a solver of the system which is nonsymmetric. Since the time required for the linear solver is very short compared to the assembly of the matrices, it is not yet our priority to improve the linear solver. We examine now the general linear characteristic of the relative errors. In Figure 6, we display the error evolution where we consider four levels for several molecules and several right hand sides. The curves and correspond to a propane molecule admitting 75 patches. We use a water cluster admitting 386 patches for and while another water cluster admitting 1109 patches are used for and. The curve corresponds

to a DNA section admitting 2119 patches. The exact solution is used for the curves till while the remaining ones correspond to the solution. The error plots lightly vary in function of the used molecules but in general all the curves exhibit the same slope characteristic. In fact, they decrease linearly in logarithmic scale in function of the BEM levels. The implemented BEM simulation is able to treat large molecules. Our program functions in parallel [40] [41] [42] on computers admitting several cores or multi-processors. The implementation was accomplished by using a message passing technique which was practically carried out by means of MPI (Message Passing Interface). The acceleration of the computation which is also known as speedup is summarized in Figure 7. The speedup quantifies the ratio between the execution time on a parallel machine having processors and the time elapsed on a single processor. The speedup curves indicate that our implementation scales well by increasing the number of processors implying that the load of computing tasks is well balanced among the processors and that the cost of inter-processor communications is not excessive. This consists of the BEM program without the linear solving which takes no more than 5 percent of the entire BEM computation (see Table 5) and which functions only sequentially for the time being. All other BEM stages function on a parallel architecture. The speedup curves concern the execution time when the number of the processors is increased for two cases: (a) various molecules possessing different patch counts, (b) increasing wavelet levels. It is beyond the scope of this paper to provide a full descrip- tion of the parallel implementation which is deferred to a subsequent article. An instance of the computed density function defined on the surface of a DNA section is depicted in Figure 8 where a triangular mesh serves only as simplification of the graphical presentation.

6. Conclusion

We constructed a surface structure which is suitable for subsequent BEM-simulation. The molecular boundary in form of Connolly surface was decomposed into globally continuous NURBS having similar surface areas. We showed outcomes of BEM simulation on different models possessing many patches. Results pertaining to accuracy

and runtimes have been reported as well. We treated several molecular models which are acquired from a molecular dynamic simulation or from realistic PDB files.

Cite this paper

Randrianarivony, M. (2016) Multiwavelet Boundary Element Method for Cavities Admitting Many NURBS Patches. Modeling and Numerical Simulation of Material Science, 6, 69-93. http://dx.doi.org/10.4236/mnsms.2016.64007

References