Modeling and Numerical Simulation of Material Science
Vol.04 No.04(2014), Article ID:50403,9 pages
10.4236/mnsms.2014.44017
Numerical and Experimental Study of the Roughness Effects on Mechanical Properties of AISI316L by Nanoindentation
Ling Chen1, Aylin Ahadi2, Jinming Zhou1, Jan-Eric Ståhl1
1Division of Production and Materials Engineering, Lund University, Lund, Sweden
2Division of Mechanics, Lund University, Lund, Sweden
Email: ling.chen@iprod.lth.se
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 29 July 2014; revised 29 August 2014; accepted 29 September 2014
ABSTRACT
Surface roughness is a commonly used criterion for characterization of surface quality in a machining operation. In the study of micro-scale mechanical properties of machined surface and cutting tool using nanoindentation method, perfect surface finish on the specimen is often required for the reliable indentation result. However, the perfect surface finish is often difficult to obtain from the machining operation due to the dynamic behavior of the machining and the limitation of the cutting tool geometry. In the presented paper, the effect of surface roughness on the nanoindentation measurements is investigated by using finite element method. A 3D finite element model with seven levels of surface roughness is developed to simulate the load-displacement behavior in an indentation process with a Berkovich indenter. The material used in the simulation is AISI 316 L stainless steel, modeled as an elastic-plastic material. The mechanical properties were calculated by combining simulations with the Oliver-Pharr method. The hardness and reduced modulus from the simulation were found to decrease with an increase of roughness. The study showed that the scatter of the load-depth curves and the deviation of the hardness and the reduced modulus are significant affected by the variation of roughness. It was also found that the height of pile-up was little affected by the surface roughness from the simulation. The combined effect of indenter tip radius and surface roughness was also investigated. The study was complemented with experimental tests and the results from these tests support the results from the simulation.
Keywords:
Nanoindentation, FEM Simulation, Surface Roughness, Elastic Modulus, Hardness

1. Introduction
It is well known that the mechanical properties at micro-scale level have significant impact on the performance of the machined component, such as fatigue, wear, corrosion resistance [1] . In the study of micro-scale mechanical properties with nanoindentation test on machined surface and cutting tool, prefect surface finish on the test specimen is often required for the reliable result [2] [3] . However, perfect surface finish is often difficult to obtain from the machining operation due to the dynamic behavior of the machining and the limitation of the cutting tool geometry. In nanoindentation, calculation of mechanical properties, such as hardness and Young’s modulus, is based on the measurement of load P and contact area, Aproj, see [4] . The contact area is not measured directly in the indentation experiment but calculated from the depth of contact and the indenter geometry. Since the contact area is obtained indirectly from the depth of penetration in sample material, the natural roughness of the specimen surface can cause errors in the determination of area in the contact between indenter and specimen. This specially applies in the coating and thin film indentation, such as coated cutting tool, mold and die, in which the indentation depth is limited by their thickness [3] . To simplify the calculation, the assumption of smooth surface and continues contact in the whole process of indentation is often made in the calculation of mechanical properties [4] . Alternatively, much larger indentation depth is required in the test, such as in Vickers indenter test, it always requires the contact depth larger than 20 times of roughness to eliminate the effect of roughness to some extent [1] .
The effects of roughness on indentation, founded in previous investigations, were mostly focused on the spherical indenter [2] - [8] . The maximum asperity height and the contact radius, was investigated using spherical indenter test by [4] and it was reported in this paper that the roughness has a significant effect when small load was applied in the test. These effects however, were reported to be less severe for sharper indenters. Babji et al. [5] studied the effect of macroscopic scale roughness, Rm, of about 1 mm, for different shape of asperities both experimentally and numerically using spherical indenter. They found that the Young’s modulus, EIT, and hardness, H, are sensitive to roughness. Furthermore a liner relationship between the effect of H and EIT was also reported. In the study made by [6] , using 2D FE-model, it was observed that the increase of the roughness causes a greater scatter of elastic modulus, EIT, in an elastic deformation material with a spherical indenter. Also [7] did atomic simulations using molecular dynamics, intending to give a physical understanding of the vicinity of the contact area indented by the rigid indenter which is difficult due to the in homogeneity of the surface properties. It was suggested that the existence of a surface step makes the load needed to nucleate the dislocations decrease significantly. Furthermore in this study, the roughness was investigated by experiment, where the sample is single-crystalline aluminum and it is prepared by electro polishing, and the roughness is measured by the atomic force microscopy (AFM). The size of the specimen in atomic simulations is however limited due to computational limitation of molecular dynamics. According to the study made by [8] , where experiment using Berkovich indenter were performed, the displacement burst is sensitive to the roughness of the sample; the initial displacement load is decrease with the increased roughness.
Results from these previous investigation based on the FEM simulation indicated the significant effect of roughness on nanoindentation test. However, these models were only focused on the 2D axisymmetric model, the spherical indenter and full elastic material, in which the true scenario of the indentation measurement was significantly simplified. Moreover, the geometry effect was often ignored in the most research. This paper presents a fully 3D finite element model and Berkovich indenter is used to simulate the effect of roughness on nanoindentation test. The hardness and reduced modulus were determined from the simulation using the Oliver and Pharr method [4] and the variation with the roughness was studied. The work was complimented with nanoindentation experiments on surface with different roughness in order to validate the results. To provide a better understanding of roughness effect in nanoindentation, different indenter tip radii were also introduced in the FE-model and the combined effect of the geometry of the indenter and the roughness of the surface were studied.
2. Simulation of Roughness
A 3D surface roughness with designed values was generated with Matlab program and then the roughness values were mapped into the Abaqus to create the FE roughness model. A flat surface was created with N × N nodes with Matlab, see [9] [10] . The height of each node was changed randomly based on the calculation from following Equations (1)-(3) to meet the designed roughness values.
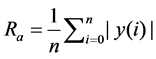 (1)
(1)
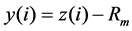 (2)
(2)
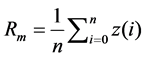 (3)
(3)
Ra is the arithmetic average of absolute values, n is the amount nodes of the surface; y(i) is the distance between the peak or valley to the mean value; z(i) is the height of each node; Rm is the mean value of all nodes height; and z(i) is generated by a random function in Matlab software. The new surfaces were created with required surface roughness through the iterative calculations employing the numerical procedure for simulation of three-dimensional surfaces that has been developed by [10] . The procedure is based on Fast Fourier Transform and allows simulating rough surfaces with given spectral density and surface roughness. To generate a three-di- mensional random roughness surface, the surface height function introduced in [10] is a Gaussian distribution on the X-Y plane. The procedure was implemented in Matlab and an example of surface with Ra = 2 nm, generated with the matrix of 100 × 100 points in the X-Y plane, is shown on Figure 1.The points serve as nodes of the top surface in the FE model.
The model was generated in Abaqus CAE with initially flat surface. Then, Matlab code was written to find the top surface nodes, and change the height of top surface nodes to the requirement of the roughness profiles according to the procedure described above. Finally, the changed top surface nodes were put into the input file, a new surface was generated and simulations performed in Abaqus. In the generation of the surface with roughness, the maximum asperities of sample roughness was chosen to be 3 times smaller, than the minimum element size. Totally, surfaces with seven different levels of roughness were generated, 2 nm, 3 nm, 8 nm, 12 nm, 20 nm, 30 nm and 42 nm. The roughness of 2 nm, 20 nm and 42 nm models are shown in Figure 2.
3. Method
Finite Element Model
The nanoindentation test on bulk materials with isotropic elastic-plastic properties was simulated using Abaqus/ Explicit 6.11 with uniaxial stress-strain data as an input. In this study, AISI316L was chosen as the reference material due to its single face simple structure. The material model used for the test specimen was Von Misses plasticity with isotropic hardening. The material parameters are specified as, [11] [12] : elastic modulus E = 210 GPa, yield stress sy = 1.1 GPa and Poisson’s ratio νS = 0.28. A 3D Berkovich indenter was modelled in this study. The indenter was considered as a rigid body, since the elastic modulus of the indenter exceeds that of the specimen, and also due to the fact that this study do not focus on the deformation of the indenter. A modified 10-node second-order tetrahedral element (C3D10M) was applied in the model and the number of elements is 2313. The specimen was modeled with 321,632 continuum 3D, eight-node reduced integration elements (C3D8R). The model assembly, in its initial state is demonstrated in Figure 2.
Figure 1. Simulation of the roughness surface with Ra = 2 nm.

Figure 2. (a) 3D FE roughness model and (b) Simulated load-displacement values for an ideal surface and experimental data for surface of roughness less that 1 nm.
The nanoindentation process was simulated both during the loading and unloading steps. In the loading pro- cess, the simulation was performed by applying a force of 5 mN in the vertical direction to a depth of 237 nm. During the process of unloading, the indenter tip returns to the original position. The contact constraint was defined by the master and slave surfaces. In the model, the indenter was the master surface and the specimen was the slave surface. A fix boundary condition was applied on the bottom of the specimen. The FE model was validated to experimental data for AISI316L. Simulation with an ideal surface was compared to experiments on a surface with roughness less than 1 nm, (see Figure 2(b)). It was found that the FE model can represent the experimental data with very good agreement.
The Young’s modulus EIT and the hardness H can be calculated according to the Oliver and Pharr method described in details in [4] and was expressed as follow:
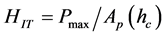 (4)
(4)
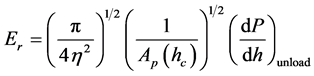 (5)
(5)
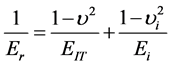 (6)
(6)
with
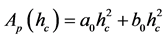 and (7)
and (7)
In above expression η = 1.034 for a Berkovich indenter, ε = 0.72 and h is the total displacement from mea-
surement. 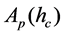 is the project area of contact, Pmax is the maximum load in the test and
is the project area of contact, Pmax is the maximum load in the test and 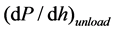 is the
is the
unloading stiffness at the depth of h. The properties of the indenter usedin the calculations are Ei = 1141 GPa, vi = 0.07. The constant a0 and b0 are fitted to the experimental curves obtained from the area function for fused silica. The reduced modulus Er represents the elastic deformation that occurs, without needing the Poisson’s ratio of the material. Therefore it was used in following.
4. Results and Discussion
4.1. Effect of Roughness
The seven models with different level of roughness were used to study the roughness effect when performing a nanoindentation test with Berkovich indenter. For each roughness, fifteen simulations were conducted. The indentation position on specimen was randomly selected in the simulations. When the indenter is located on a peak the contact area is larger than the ideal case and when the indenter is located on a valley it is smaller. Since the force controlled method was applied in the simulation, the initial position of the indenter tip plays an important role. The zero point was set to the displacement when the load was over zero initially. In all simulation, the correction with the initial zero point selection was applied and the initial load was 0.03 mn. This results in different initial depths for the models with different roughness. For example for the roughness Ra = 2 nm the initial depth is between 80 - 120 nm for the Ra = 20 nm the initial depth between is 50 - 124 nm and for the Ra = 42 nm the initial depth is between 20 - 130 nm. The correction of the initial point will generate the different values when calculating the hardness modulus using the Oliver-Pharr method.
The initial load-displacement curves for three different roughness models were studied and the effect of roughness is clearly observed in Figure 3, where the load-displacement curves for each roughness is presented for in-
Figure 3. Load-displacement (on the left) and unloading curves (on the right) for different roughness levels.
dention load of P = 5 mN. As expected, the data scatter is increasing with the increasing roughness. This scatter is due to high surface roughness and it is a frequently encountered problem when trying to characterize the mechanical properties at shallow nanoindentation depth.
The strain distribution at indentation loads of 1.5 and 5 mN is shown in Figure 4 for two levels of roughness, 2 and 42 nm. The surface roughness distribution gives rise to the asymmetric distribution of the strain in the beginning of the nanoindentation test. As seen in Figure 4(b), the disorder of the strain distribution is still present at load 5 mN for the Ra = 42 nm, whereas for Ra = 2 nm the strain distribution becomes axisymmetric, as seen in Figure 4(d).
The deformation profiles for the three roughness models are seen in Figure 5. The pile-up effect is clearly observed here and this effect is larger for the surface with higher roughness, see Figure 5(b). However, the pro- ject area is not the same and when the roughness is increasing; the project area is decreasing, which also affects the values for the hardness and the reduced modulus.
The reduced modulus and hardness are calculated for different surface roughness using the Oliver-Pharr method described in [13] . This method involves calculation of the contact area and contact depth, and it is found that the amplitude of surface roughness has effect both on the contact area between indenter and specimen material and the contact depth as well. The calculated values are presented on Figure 6. As expected the scatter of hardness and reduced modulus is increasing with the increased roughness. It is also seen from Figure 6, that the increase of the surface roughness results in decreasing of reduced modulus and the hardness.
In the ideal model, i.e. the model without roughness the reduced modulus was calculated to Er = 190.6 GPa, and hardness to H = 2.56 GPa. As seen from Figure 6 for Ra = 2 nm, the results from the simulations are closely to the results from simulations onthe ideal surface. The mean values for each roughness are seen on Table 1. As seen the hardness and reduced modulus increase with the higher level of roughness. This is partly because the roughness surface changes the elastic-plastic deformation in the material subjected to indentation. From the unloading curve on Figure 3, it is seen that for the surface with larger roughness the unloading stiffness is smaller. From the contact depth equation 7, this will lead to a smaller contact depth and contact area. Finally the hardness of the material is increasing with decreasing contact depth, i.e. with increasing roughness. This was clearly observed from simulations results.
The indentation depth h in nanoindenation is affected by the roughness. To account for this dependence ratio h/Ra is interesting to study and the hardness and the reduced modulus were also plotted as a function of the ratio h/Ra in Figure 7. This ratio is small for high level of roughness and increases with decreasing roughness. As it is seen from Figure 7 for small roughness the values of both the hardness and the reduced modulus reach a constant
Figure 4. Strain distribution under different loads for Ra = 42 nm ((a), (b)) and Ra = 2 nm ((c), (d)).

Figure 5. The plastic deformation profiles affected by subsurface roughness. (a) Displacement in the vertical direction, cross-section of Ra =20 nm. (b) Pile-up profile of Ra =2, 20, 42 nm.

Figure 6. Numerical result for the hardness H (a) and reduced modulus Er (b) for the eight different roughness Ra=2 nm, 3 nm, 8 nm, 12 nm, 20 nm, 30 nm, 42 nm.
Table 1. The hardness H and reduced modulus Er from simulations for different roughness at load the load P = 5 mN.
Figure 7. Evolution of Er and H at P = 5 mN as a function of h/Ra.
values of about H = 2.25 GPa and Er = 220 GPa.
4.2. Effect of Tip Radius in Roughness
The geometrical effects of the tip radius were studied in our previous work [13] . In this study, the effect of the tip radius in combination of the specimen roughness was simulated. The reduced modulus and hardness are calculated for the roughness of 20 nm and the three different tip radii, 35 nm, 80 nm and 120 nm, see Figure 8. It was found that the tip radius has little effect when roughness is introduced in the model, when calculating the hardness. It is seen from Figure 8(a) that the hardness is somewhat increasing with the increase of the tip radius. The same hold also for the reduced modulus
4.3. Experimental Investigation
The nanoindentation tests of the Berkovich type were carried on the Nano-Test Vantage (Co. Micro material, UK), at room temperature, 20˚C. Several others environment factors as for example the vibration and humility, are controlled in the cabinet of the instrument. All indentations were performed in compliance with ISO 14577 and ASTM E2546-07. The material is AISI316L, which is a single phase stainless steel, the composition is 70 wt.% Fe, 18wt.%Cr, 11wt.% Ni, 1 wt.% Mo. The only phase present is austenite, and the grain size range is 13 um - 168 um. Five levels of surface roughness (1 nm, 2 nm, 3 nm, 8 nm and 42 nm) were generated with different polishing. At each load step the effect of roughness were studied statistically by performing a grid nanoindentation with the 10 by 10 matrix, resulting in a 100 different tests. The tip radius of the indenter in all experiments was 120 nm.
The reduced modulus and hardness were calculated for the five different surface roughness using the Oliver- Pharr method described in [13] and the results are presented in Figure 9, where the hardness and the reduced modulus are plotted as a function of the roughness level. As seen from Figure 9 the results from the experiments have the same pattern as the simulation results on Figure 6, with increasing values of the hardness and the reduced modulus. The hardness and the reduced modulus were also plotted as a function of the ratio h/Ra in Figure 10. As it is seen from Figure 10 for small roughness the values of both the hardness and the reduced modulus reach a constant values of about H = 2.25 GPa and Er = 220 GPa. This results support the finding from the simulation. However the mean values, presented on Table 2, obtained from the experiments slightly differ from the simulation values presented on Table 1. This can partly be explained by the fact that the material model used in the simulation does not take into account the grained microstructure of the material.
5. Conclusions
The effects of surface roughness and indenter tip radius on nanoindentation measurement were simulated by developing a 3D FE roughness model loaded with Berkovich indenter. The 3D roughness surface was generated in Matlab and imported into Abaqus. Models with seven roughness levels were built and used to simulate the nanoindentation test. It was found that the elastic-plastic behavior is affected by the surface roughness and a scatter of the reduced modulus and the hardness was observed. The levels of the scatter increase with the rise of roughness level. It was found, that the increase of the surface roughness results in decreasing of reduced modulus and the hardness. The mean values of the hardness are increasing with an increased roughness. However, when studying the hardness and the reduced modulus as a function of the ratio h/Ra, it was observed that for decreasing roughness the values of both the hardness and the reduced modulus reach constant values. This was also supported from the experimental tests performed for five different roughness levels.
Little effect of roughness was found in height of pile-up during the indentation deformation profile. The results from the simulations of combined effect of tip radius and roughness indicate that the sensitive of radius in roughness is not obvious when considering the scatter of load-depth curve, and there is no significant effect on the hardness and the reduced modulus. The results from the simulations showed that the tip radius has little effect on the hardness and the reduced modulus, when roughness is introduced in the model. Finally roughness leads to underestimation of the hardness and reduced modulus in the nanoindentation test. For specimen with rougher surface, the larger indentation depth should be applied in order to reach more stable test values. The hardness and reduced modulus tend to be more stable when ratio of h and Ra value is over 100 for 316 L steel.

Figure 8. The reduced modulus and hardness of different radius in Ra = 20 nm. (a) H vs. rtip in Ra = 20 nm under P = 5 mN. (b) Er vs. rtip in Ra = 20 nm under P = 5 mN.

Figure 9. Experimental result for the reduced modulus Er (a) and hardness H (b) for the five different roughness levels and experiment Ra = 1 nm, 2 nm, 3 nm, 8 nm and 42 nm.
Figure 10. Evolution of Er and H for at P = 5 mN as a function of h/Ra.
Table 2. The hardness H and reduced modulus Er from experiments for different roughness at load P = 5 mN.
Acknowledgements
This work is a part of the strategic research program under the Sustainable Production Initiative SPI. Authors would appreciate the help from Dr. V. Bushlya in sample preparation. The finite element simulations were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at LUNARC.
References
- ISO (2002) Metallic Materials—Instrumented Indentation Test for Hardness and Materials Parameters —Part 1: Test Method, in Part 1: Test method Iso. Geneva, Switzerland.
- Warren, A.W. and Guo, Y.B. (2006) Machined Surface Properties Determined by Nanoindentation: Experimental and FEA Studies on the Effects of Surface Integrity and Tip Geometry. Surface & Coatings Technology, 201, 423-433. http://dx.doi.org/10.1016/j.surfcoat.2005.11.139
- Bhushan, B., Gupta, B.K. and Azarian, M.H. (1995) Nanoindentation, Microscratch, Friction and Wear Studies of Coatings for Contact Recording Applications. Wear, 181, 743-758. http://dx.doi.org/10.1016/0043-1648(95)90191-4
- Fischer-Cripps, A.C. (2011) Nanoindentation. 3rd Edition, In: Ling, F.F., Ed., Mechanical Engineering, Vol. 1, Killarney Heights, New South Wales, 272.
- Bobji, M.S., Shivakumar, K., Alehossein, H., Venkateshwarlu, V. and Biswas, S.K. (1999) Influence of Surface Roughness on the Scatter in Hardness Measurements—A Numerical Study. International Journal of Rock Mechanics and Mining Sciences, 36, 399-404. http://dx.doi.org/10.1016/S0148-9062(99)00009-1
- Walter, C., Antretter T., Daniel, R. and Mitterer, C. (2007) Finite Element Simulation of the Effect of Surface Roughness on Nanoindentation of Thin Films with Spherical Indenters. Surface and Coatings Technology, 202, 1103-1107. http://dx.doi.org/10.1016/j.surfcoat.2007.07.038
- Bolesta, A.V. and Fomin, V.M. (2009) Molecular Dynamics Simulation of Sphere Indentation in a Thin Copper Film. Physical Mesomechanics, 12, 117-123. http://dx.doi.org/10.1016/j.physme.2009.07.003
- Shibutani, Y. and Koyama, A. (2004) Surface Roughness Effects on the Displacement Bursts Observed in Nanoindentation. Journal of Materials Research, 19, 183-188. http://dx.doi.org/10.1557/jmr.2004.19.1.183
- Gascón, F. and Salazar, F. (2011) Simulation of Rough Surfaces and Analysis of Roughness by MATLAB. In: Ionescu, C.M., Ed., MATLAB—A Ubiquitous Tool for the Practical Engineer, InTech, Rijeka, 391-420.
- Wu, J.J. (2000) Simulation of rough surfaces with FFT. Tribology International, 33, 47-58. http://dx.doi.org/10.1016/S0301-679X(00)00016-5
- Nascimento, F.C., Foerster, C.E., da Silva, S.L.R., Lepienski, C.M., Siqueira, C.J.D. and Alves, C. (2009) A Comparative Study of Mechanical and Tribological Properties of AISI-304 and AISI-316 Submitted to Glow Discharge Nitriding. Materials Research-Ibero-American Journal of Materials, 12, 173-180.
- Pelletier, H., Krier, J., Cornet A. and Mille, P. (2000) Limits of Using Bilinear Stress-Strain Curve for Finite Element Modeling of Nanoindentation Response on Bulk Materials. Thin Solid Films, 379, 147-155. http://dx.doi.org/10.1016/S0040-6090(00)01559-5
- Chen, L., Ahadi A., Zhou, J. and Ståhl, J.-E. (2012) Characterization of Mechanical Properties of Machined Surface by Nanoindentation—Part 1: Simulation of Indenter Geometry Effects, in SPS12LUCATORG: 011201100. Linköping, 191-198.
















