Modeling and Numerical Simulation of Material Science
Vol.4 No.1(2014), Article ID:41663,6 pages DOI:10.4236/mnsms.2014.41002
A Solute Pinning Approach to Solute Drag in Multi-Component Solid Solution Alloys
1Gränges Technology, Finspång, Sweden
2Department of Materials Science and Technology, Norwegian University of Science and Technology (NTNU), Trondheim, NorwayEmail: emmanuel.hersent@granges.com, knut.marthinsen@ntnu.no, erik.nes@ntnu.no
Copyright © 2014 Emmanuel Hersent et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Emmanuel Hersent et al. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received November 11, 2013; revised December 11, 2013; accepted December 18, 2013
Keywords: Boundary Mobility; Solute Drag; Multi-Component Alloys; Analytical Modelling
ABSTRACT
The Cahn, Lücke and Stüwe theory remains the backbone of more complex analysis dealing with solute drag, however, the mathematical treatment is rather involved. A new approach based on solute pinning the boundary has therefore recently been suggested, which has the main advantage of a simpler mathematical treatment. In the present paper this approach has been generalized to take into account the influence of different types of solute atoms in the high solute content/low driving force regime.
1. Introduction
It is well known that segregated impurity atoms can drastically reduce the mobility of grain boundaries in pure metals. The phenomenon is considered to be a general effect and is usually referred to simply as “solute drag”. Cahn [1] and Lücke and Stüwe [2] suggested a quantitative treatment of the solute drag, which has been the basis of following works on solute drag. The latter works have mainly focused on extending their approach to a migrating phase boundary into a multi-component system [3-9]. One achievement of the Cahn-Lücke-Stüwe theory (CLS theory) was to demonstrate that the grain boundary velocity is inversely proportional to the solute concentration in the high solute content/low driving force regime.
However this theory presents some major drawbacks. Firstly, while the basic physical idea behind the solute drag theory is principally simple, where the motion of a grain boundary is slowed down by solute atoms which exert a drag force on the boundary, the analytical treatment becomes rather involved: the solute profile around the moving grain boundary must be established by solving Fick’s first law in a moving frame and then the solute drag is determined from this profile. Secondly, few works have tackled the issue of the influence of different types of solute atoms on a moving grain boundary [10,11]. This issue is of industrial relevance because industrial alloys are generally not high purity alloys with only one type of impurity but in most cases made up of different major additions. The last decades have seen the advent of computer aided material science and engineering and so a solute drag approach taking simply into account the effect of different additions should be of great help to achieve more realistic simulations.
2. The Solute Pinning Approach
Recently a new solute drag model has been proposed based on a solute pinning approach [12]. The grain boundary is pinned by the solute atoms along the boundary, which will induce a local cusping of the boundary at the solute atoms (Figure 1). Stress concentration will arise promoting thermal activation of solute atoms out of the boundary. Compared to the CLS theory, the main benefit of this approach is to be computationally simpler. The present treatment aims to generalize this approach to different types of solute atoms in the high solute content/ low driving force regime. Then let us consider two solutes A and B in a matrix forming an ideal solid solution.

Figure 1. Representation of the force 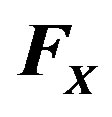 exerted by the boundary of thickness λ on the solute atoms due to its cusping, of the energy profiles across the boundary when an atom jumps either out the boundary or with it, with
exerted by the boundary of thickness λ on the solute atoms due to its cusping, of the energy profiles across the boundary when an atom jumps either out the boundary or with it, with  the activation energy for self-diffusion and
the activation energy for self-diffusion and 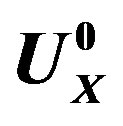 the interaction energy between the solute atoms and the boundary (for further details see [12]). (a) Stationary boundary, (b) moving boundary.
the interaction energy between the solute atoms and the boundary (for further details see [12]). (a) Stationary boundary, (b) moving boundary.
2.1. Establishment of the Equations to Solve
In steady state conditions the concentration of each type of solute atoms adsorbed at the grain boundary remains constant, which means that the rate per unit area at which the solute atoms leave the boundary 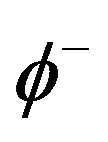 is equal to the rate at which the solute atoms arrive
is equal to the rate at which the solute atoms arrive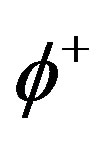 :
:
 (1)
(1)
In terms of thermal activation, following [12], the leaving rate 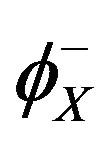 can be expressed as follows:
can be expressed as follows:
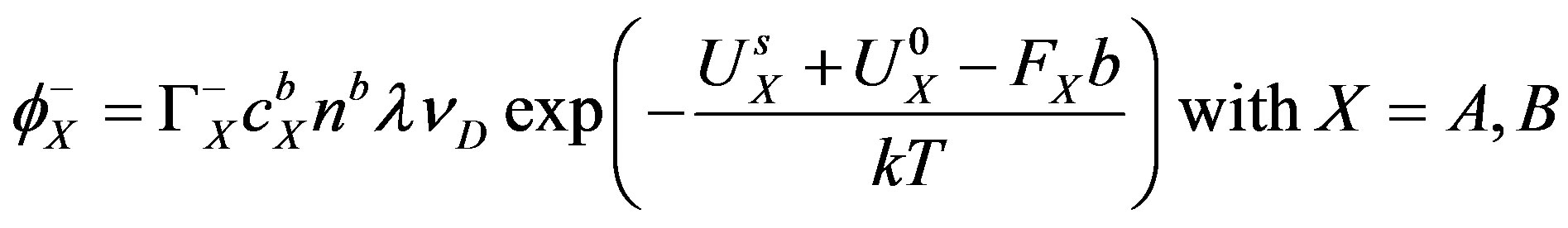 (2)
(2)
where  is a constant,
is a constant,  the boundary concentration of the solute X given in terms of atomic fraction,
the boundary concentration of the solute X given in terms of atomic fraction, 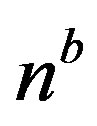 the number of atomic sites per unit volume inside the boundary,
the number of atomic sites per unit volume inside the boundary, 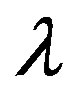 the boundary thickness,
the boundary thickness, 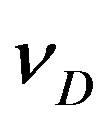 the Debye frequency,
the Debye frequency, 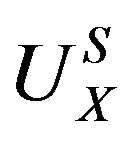 the diffusion activation energy for the solute X,
the diffusion activation energy for the solute X, 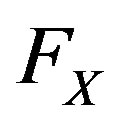 the cusping force on each solute atom of type X exerted by the boundary reducing thus the activation barrier out of the boundary by the energy
the cusping force on each solute atom of type X exerted by the boundary reducing thus the activation barrier out of the boundary by the energy  and b the close packed spacing in the matrix. Some parameters are pictured in Figure 1.
and b the close packed spacing in the matrix. Some parameters are pictured in Figure 1.
The arrival rate 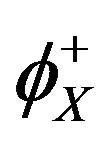 can be written as follows:
can be written as follows:
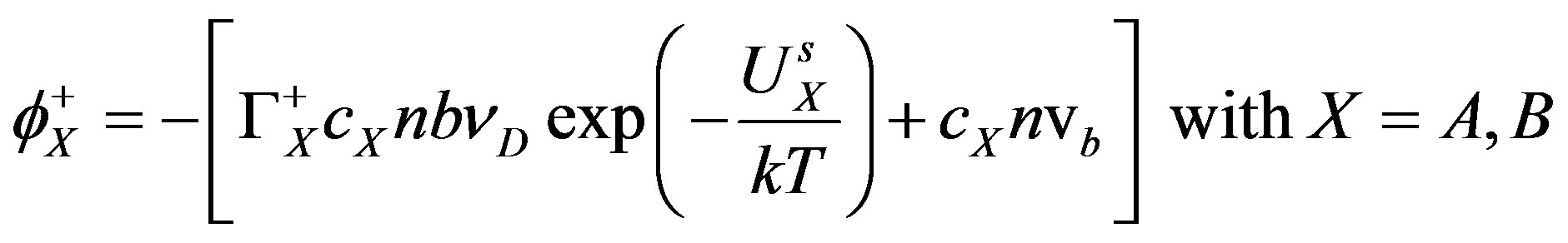 (3)
(3)
where 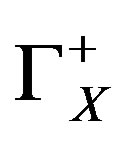 is a constant,
is a constant, 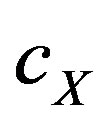 is the bulk solute concentration in atomic fraction of the solute X, n the number of atomic site per unit volume in the bulk of the material. The arrival rate
is the bulk solute concentration in atomic fraction of the solute X, n the number of atomic site per unit volume in the bulk of the material. The arrival rate 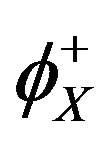 is made of two terms: the first term represents the diffusion contribution to the arrival rate
is made of two terms: the first term represents the diffusion contribution to the arrival rate 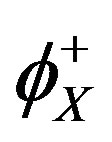 and the second term a convective contribution (i.e. sweeping up of solute atoms ahead of the moving boundary). Introducing the expressions for
and the second term a convective contribution (i.e. sweeping up of solute atoms ahead of the moving boundary). Introducing the expressions for 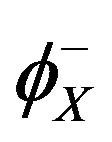 and
and 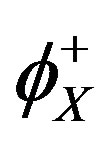 in Equation (1) makes possible to calculate the boundary concentration
in Equation (1) makes possible to calculate the boundary concentration  provided an expression for the migration rate
provided an expression for the migration rate 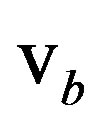 is obtained.
is obtained.
By statistical considerations of the probability that a solute atom leaves the boundary, the boundary velocity  has been established in [12] as equal to
has been established in [12] as equal to
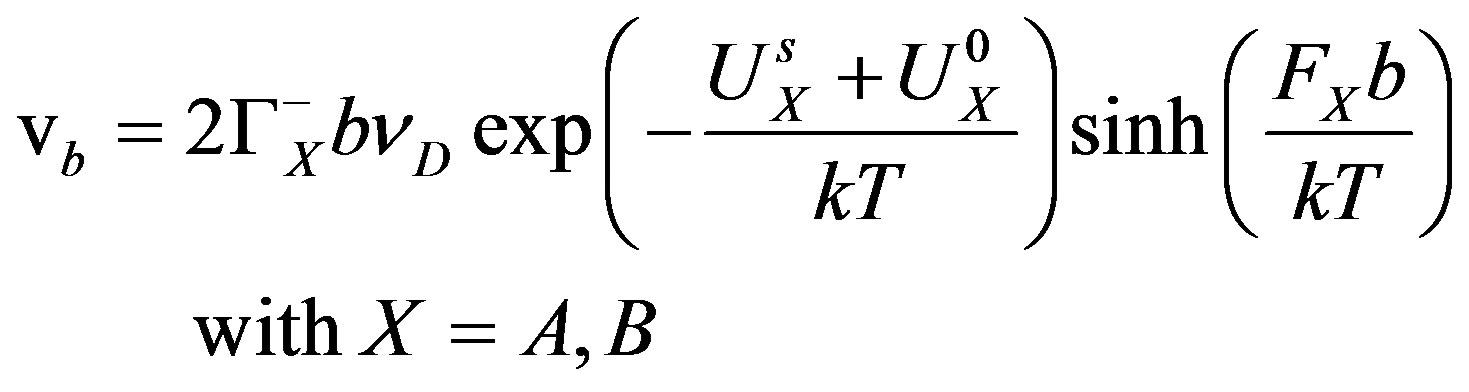 (4)
(4)
By combining the expressions obtained for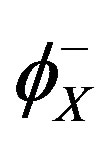 ,
, 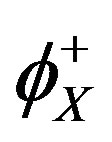 and
and 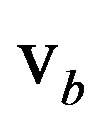 with Equation (1) and by assuming
with Equation (1) and by assuming  to be approximately of the same size of
to be approximately of the same size of 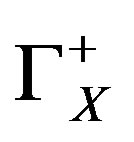 (represented by a common symbol
(represented by a common symbol 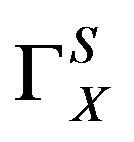 in the following), the following expressions for the boundary solute concentrations are obtained:
in the following), the following expressions for the boundary solute concentrations are obtained:
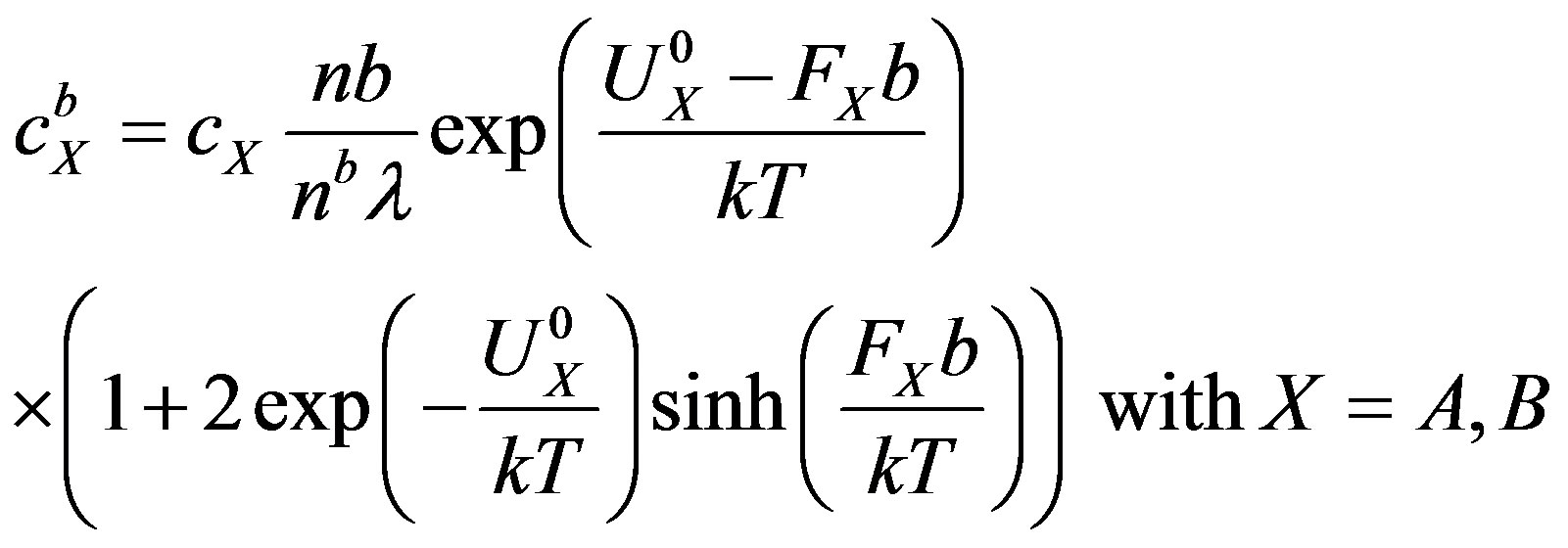 (5)
(5)
Further in the paper it will be assumed that the number of atomic sites per unit area of the boundary 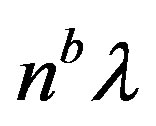 is nearly equal to the number of atomic sites per unit area inside the matrix
is nearly equal to the number of atomic sites per unit area inside the matrix .
.
The boundary velocity can also be expressed in terms of mobility. In pure materials, grain boundary migration theory predicts that the boundary velocity 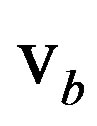 can be expressed as the product of two terms—the intrinsic mobility
can be expressed as the product of two terms—the intrinsic mobility 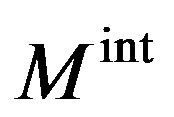 of the pure grain boundary and the driving pressure P:
of the pure grain boundary and the driving pressure P:
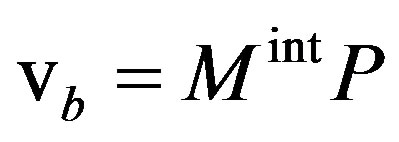 (6)
(6)
Based on the probability of jumps forward and backward through the grain boundary, 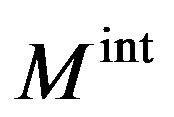 can be written as [13]
can be written as [13]
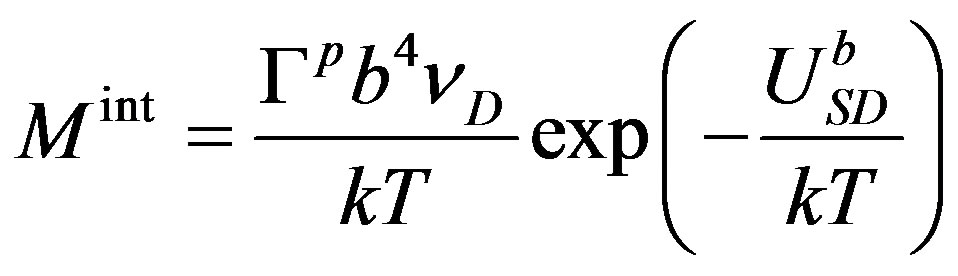 (7)
(7)
In this equation 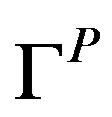 is a constant and
is a constant and 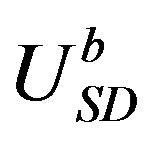 is an activation energy associated with boundary migration. This activation is typically found to have a value half that of self-diffusion.
is an activation energy associated with boundary migration. This activation is typically found to have a value half that of self-diffusion.
However for metals containing solute atoms the above linear relationship Equation (6) can still be applied to determine the velocity of the grain boundary regions free of solute atoms if P is replaced by a new driving pressure which is the difference between the driving pressure P and the restraining pressure  resulting from the interactions between the solute atoms and the grain boundary
resulting from the interactions between the solute atoms and the grain boundary
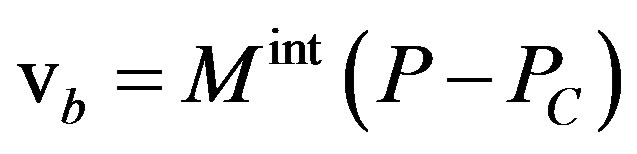 (8)
(8)
In the latter expression, the pressure coming from grain boundary curvature is neglected, which assumes that the grain boundary remains macroscopically planar during its migration.
The atoms A and B respectively in number 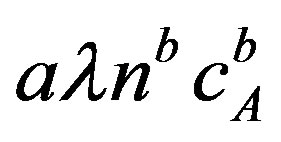 and
and 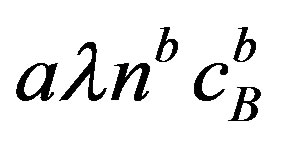 exert a force
exert a force 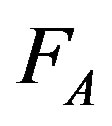 and
and 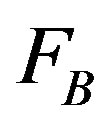 on a grain boundary of area a. Thus the restraining pressure
on a grain boundary of area a. Thus the restraining pressure 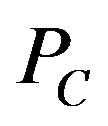 can be determined as
can be determined as
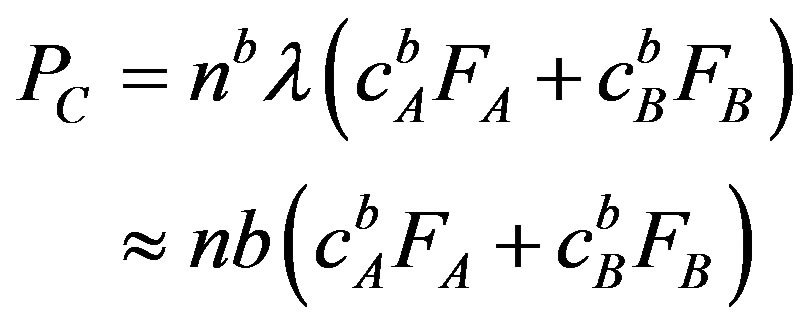 (9)
(9)
In the special case of a low driving pressure/high solute content, i.e.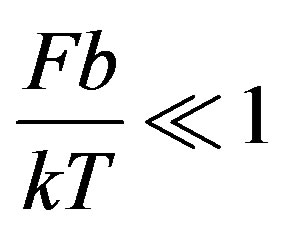 , it appears that the grain boundary moves with a velocity proportional to the driving pressure. The proportionality factor is determined by the solute content in solid solution. So an extrinsic mobility
, it appears that the grain boundary moves with a velocity proportional to the driving pressure. The proportionality factor is determined by the solute content in solid solution. So an extrinsic mobility 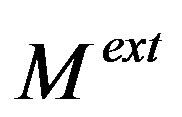 can be defined:
can be defined:
 (10)
(10)
The solute pinning approach gives an expression of this extrinsic mobility in terms of the relevant parameters at the atomic scale [12]:
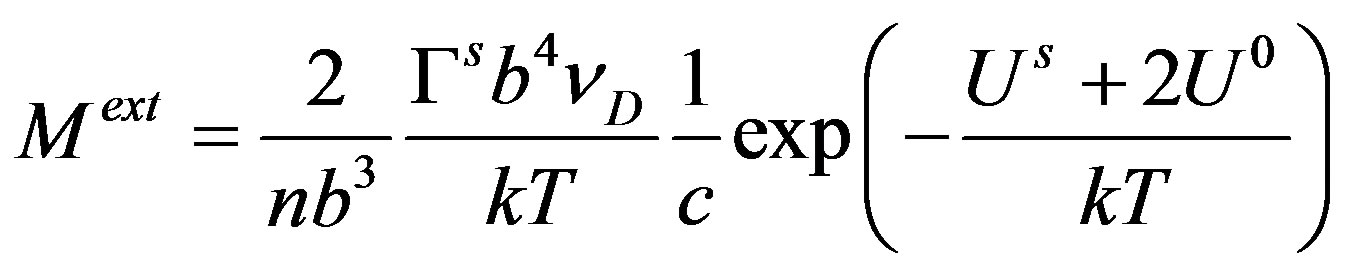 (11)
(11)
Finally two more relations can be obtained by pointing out that the grain boundary velocity must be independent on which elements used to determine the velocity:
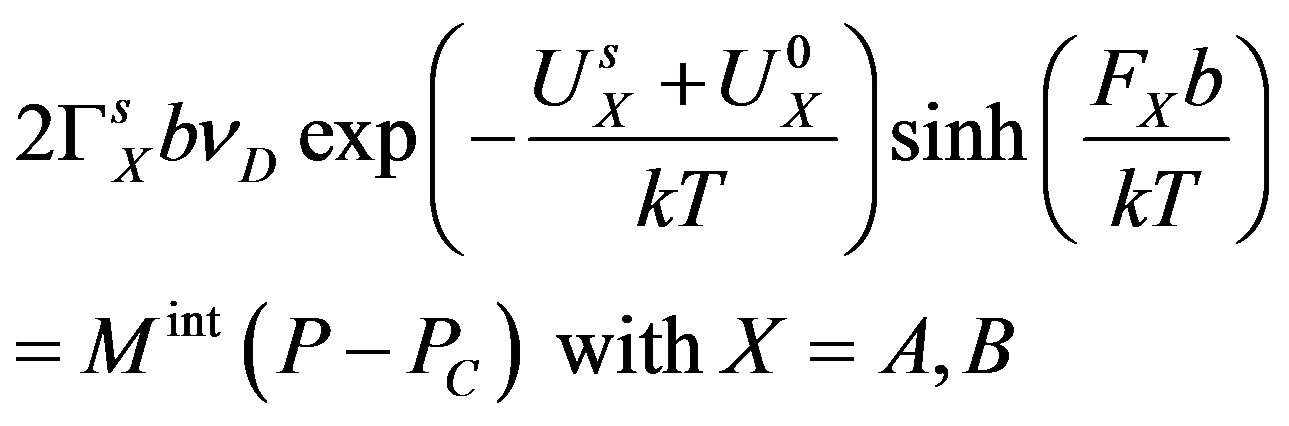 (12)
(12)
By introducing the expressions for the intrinsic mobility 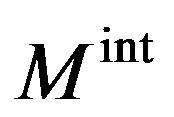 (Equation (7)) and the restraining pressure
(Equation (7)) and the restraining pressure 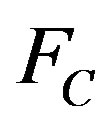 (Equation (9)) the following non-linear system can be obtained:
(Equation (9)) the following non-linear system can be obtained:
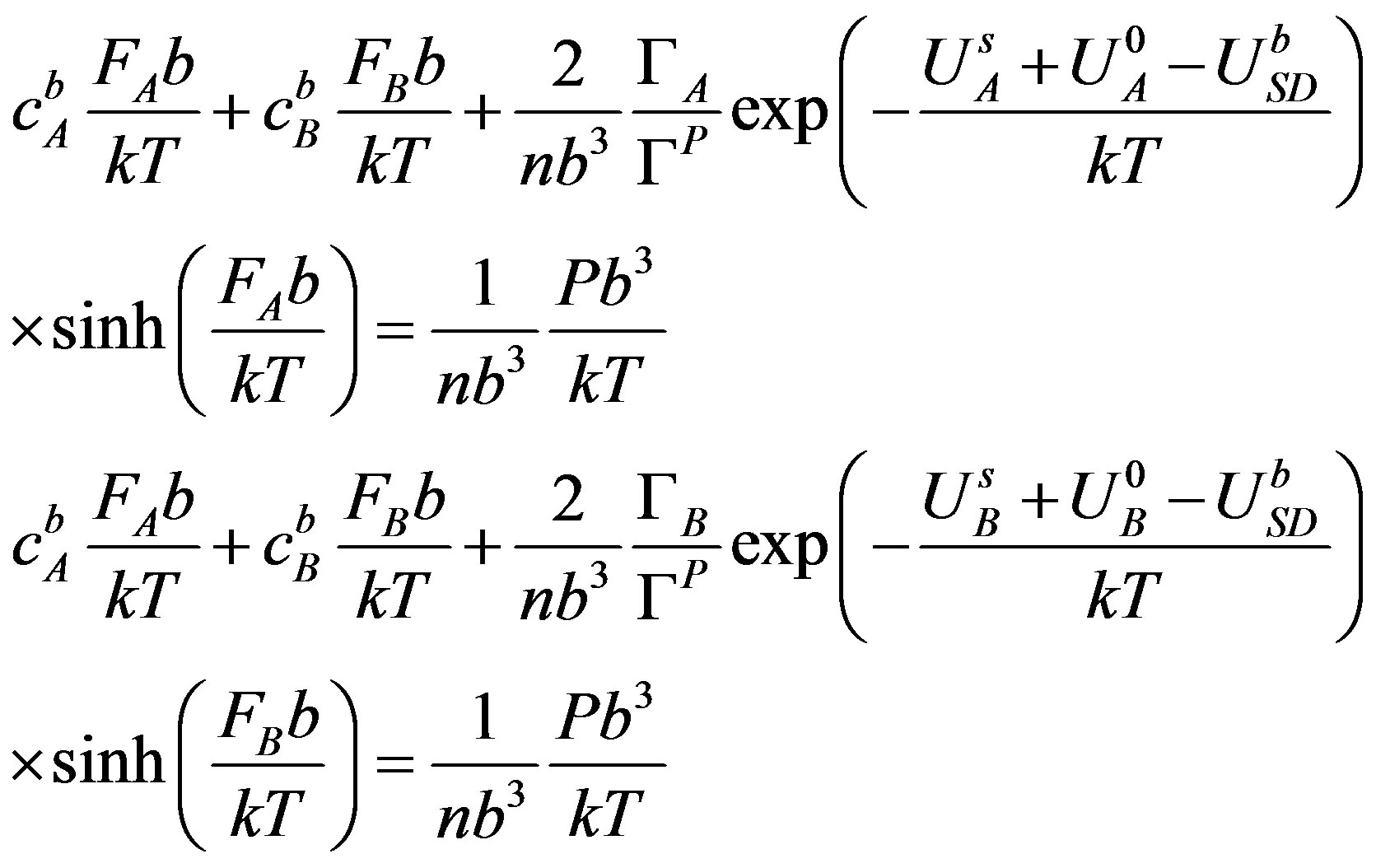 (13)
(13)
To simplify the notations the following normalized variables are introduced:
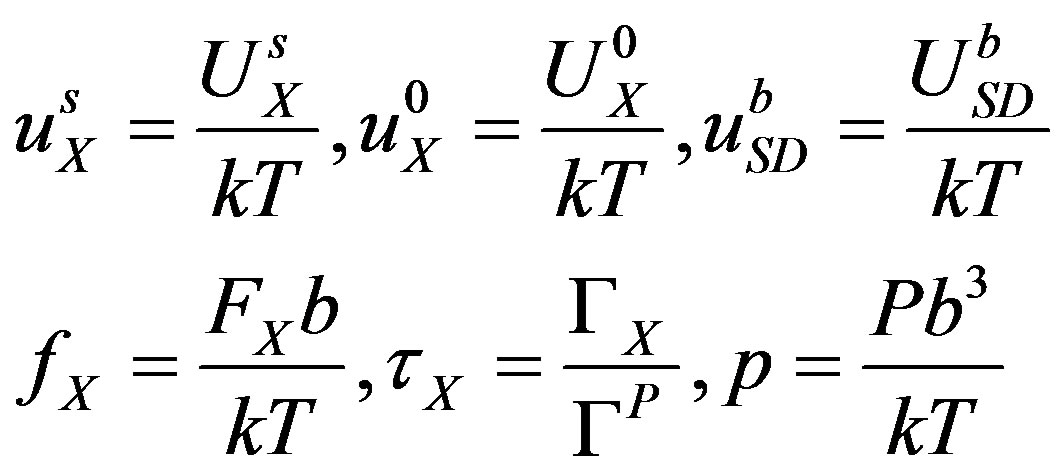
The system becomes then:
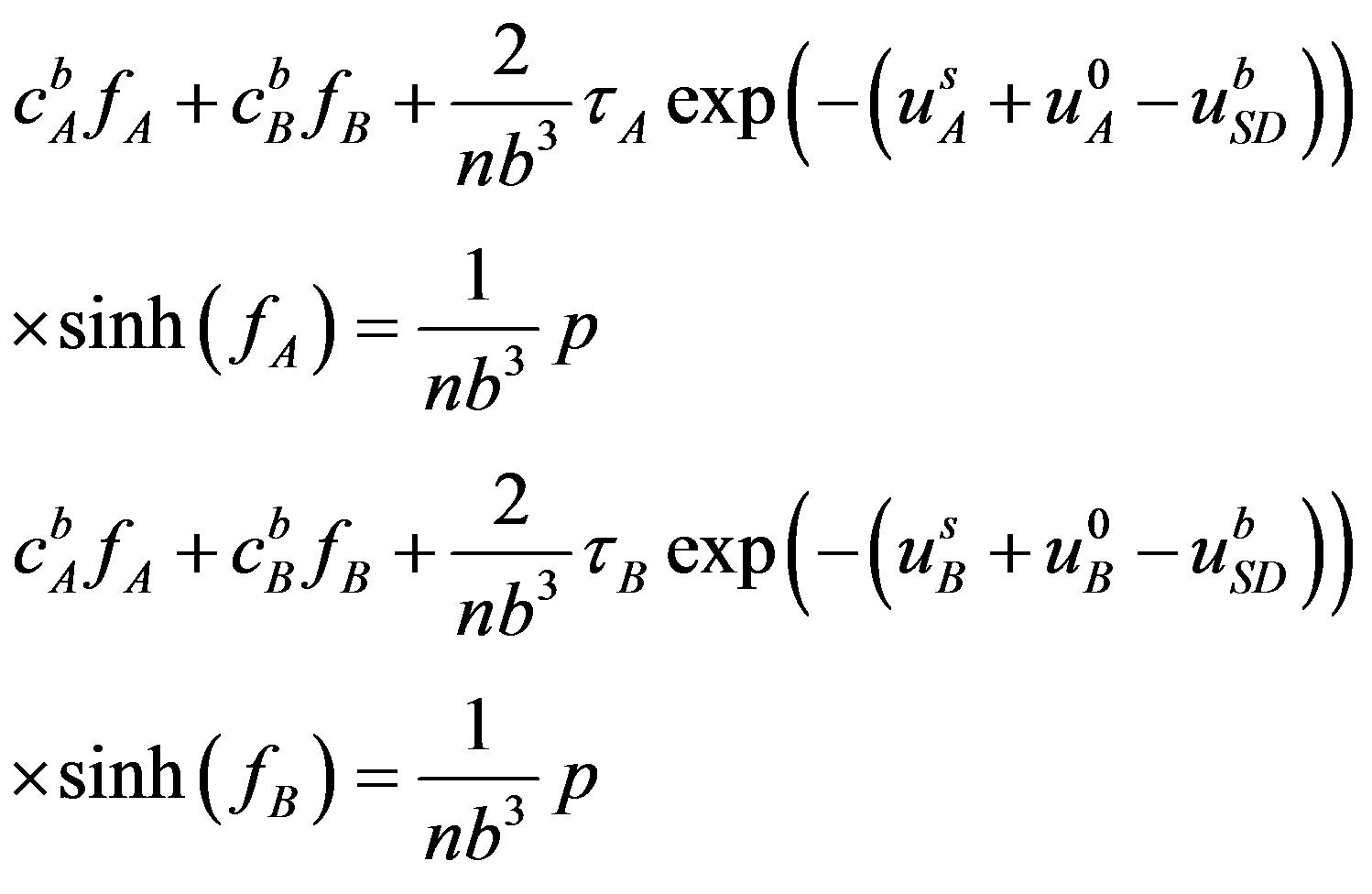 (14)
(14)
Solving this system for any conceivable case may be quite challenging because of its non-linearity and the coupling between the cusping forces 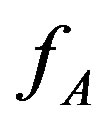 and
and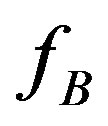 . In the present paper we will therefore only solve this system for the case of
. In the present paper we will therefore only solve this system for the case of  and
and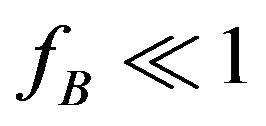 . These assumptions imply that the solute content is high enough to impede the grain boundary motion.
. These assumptions imply that the solute content is high enough to impede the grain boundary motion.
2.2. Linearization of the System
The system can in this case be linearized as follows:
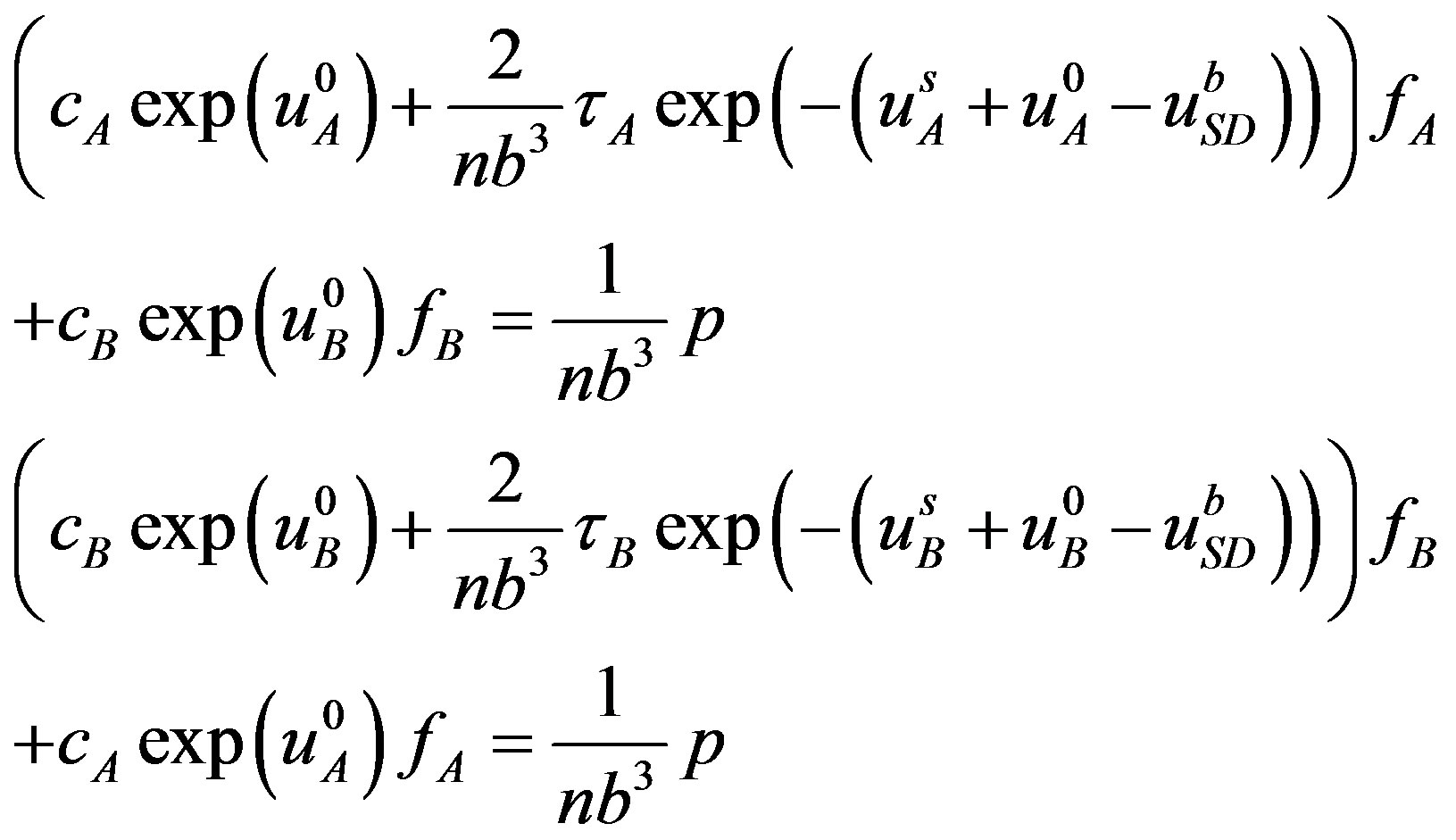 (15)
(15)
By using the Crammer’s formula for the solutions of a linear system, the expressions for  and
and 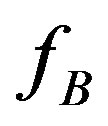 could be easily obtained:
could be easily obtained:
 (16)
(16)
with  the system determinant whose expression is
the system determinant whose expression is
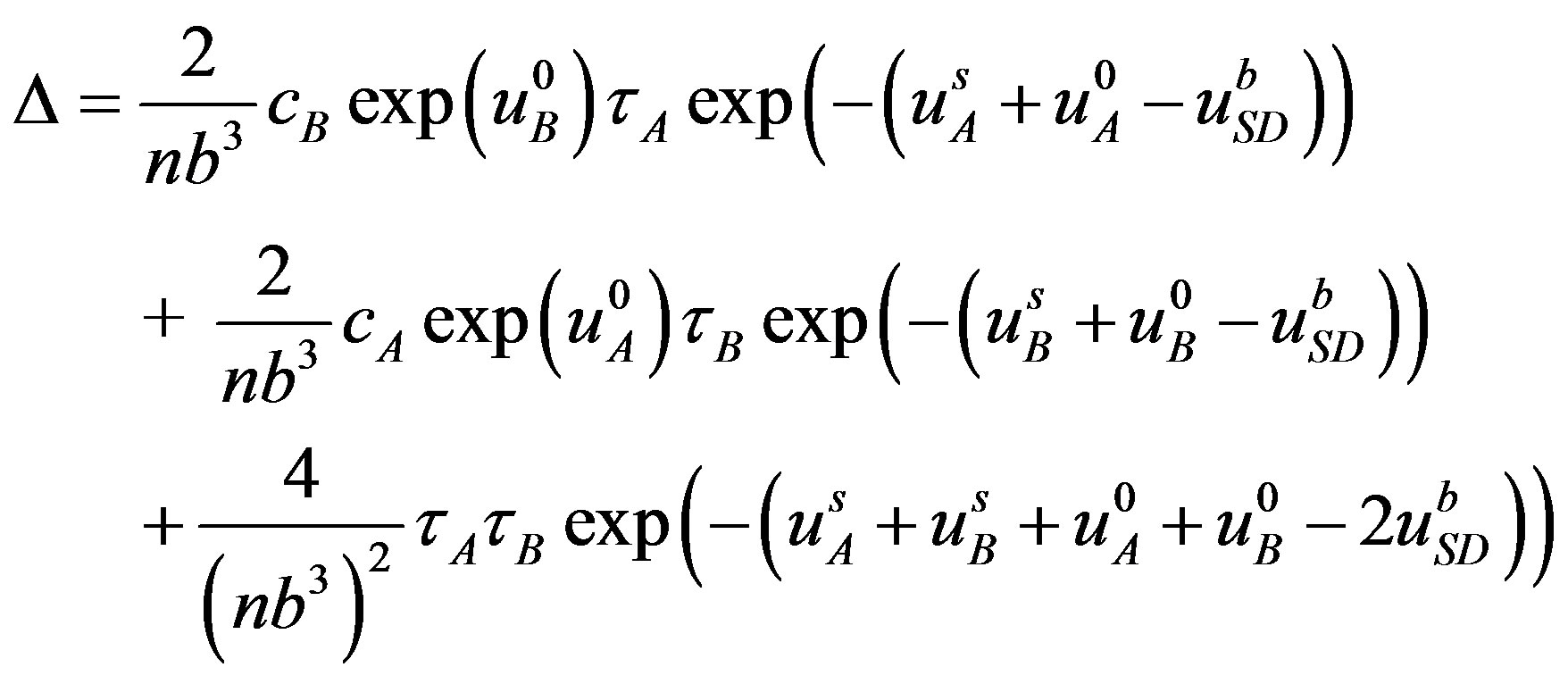
It should be noted that the expression for 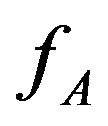 and
and 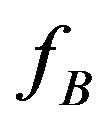 as given by Equation (16) are symmetrical. To obtain an expression of the boundary velocity independent of the element considered, the grain boundary velocity has to be written as
as given by Equation (16) are symmetrical. To obtain an expression of the boundary velocity independent of the element considered, the grain boundary velocity has to be written as
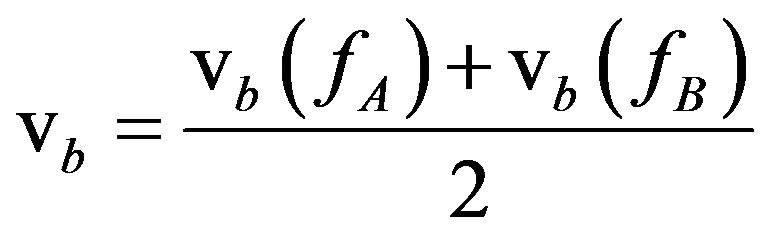 (17)
(17)
By linearizing the expressions for the boundary velocity  (Equation (4)) and inserting them in Equation (17), the boundary velocity
(Equation (4)) and inserting them in Equation (17), the boundary velocity 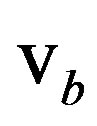 can finally be expressed as
can finally be expressed as
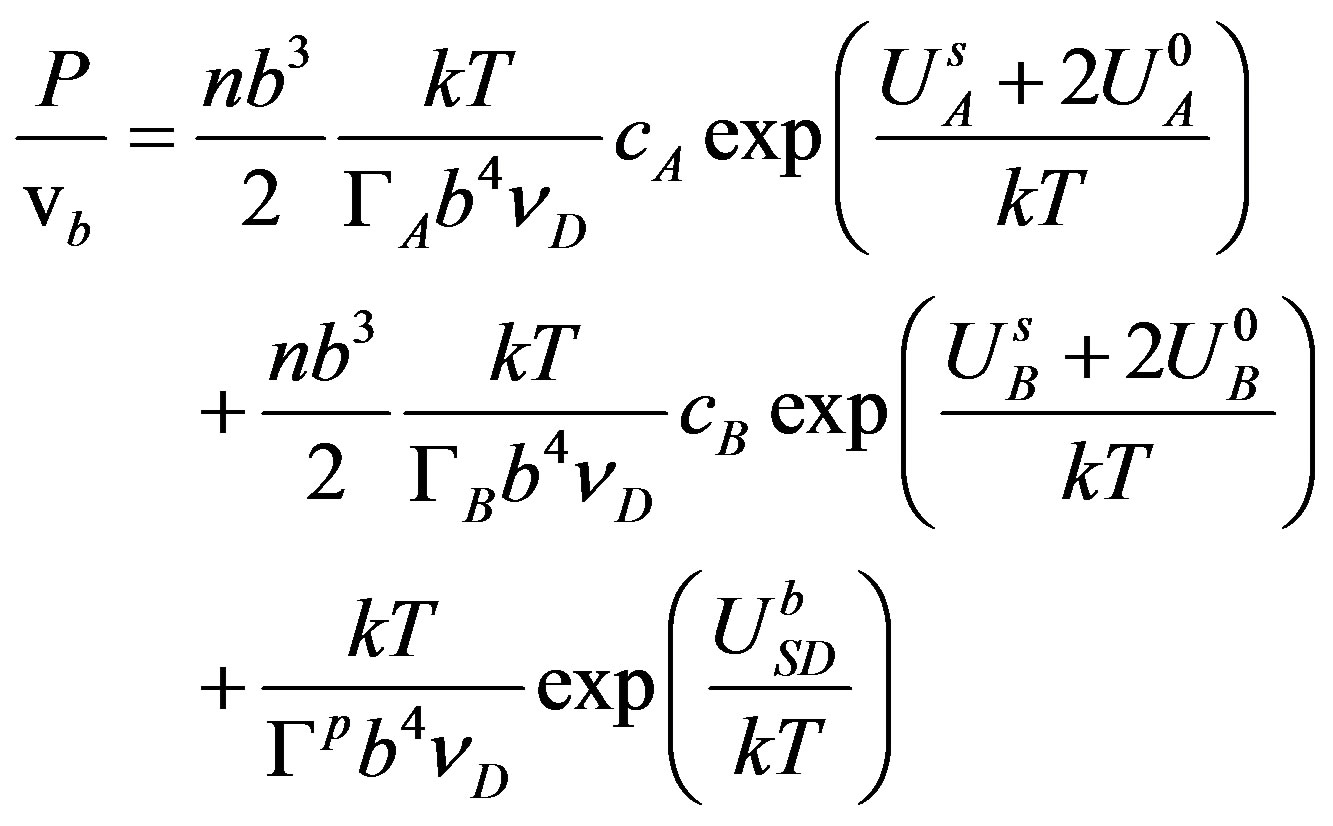 (18)
(18)
By writing the latter expression with the help of the intrinsic and extrinsic mobilities, respectively Equation (7) and Equation (11), the relation between the boundary velocity  and the driving pressure P takes the form
and the driving pressure P takes the form
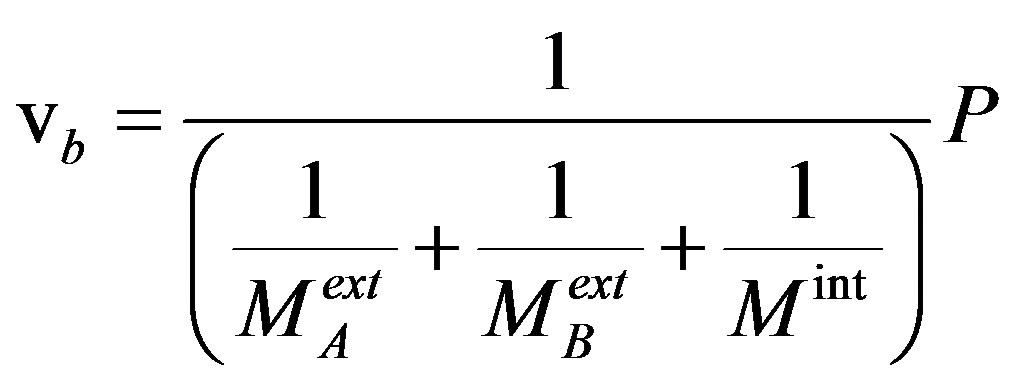 (19)
(19)
The present solute pinning approach thus permits to find a very compact and convenient formula for the extrinsic mobility of a grain boundary in the case of different types of solute in solid solution in the high solute content/low driving force regime. The demonstration done for two different types of solute can easily be generalized for n different types of solute by using the expressions of the solutions of a linear system in terms of the determinant.
3. Discussion
The Equation (19) is actually consistent with an analogous one that can be derived by following Lücke and Detert’s original demonstration of solute drag [14] (the CLS theory has been developed later to overcome the shortcomings of this simple approach but do not change fundamentally the result). Indeed, in their approach it is assumed that a slow moving boundary will drag along its migration a number of solute atoms A and B close to their equilibrium values, which is equal to
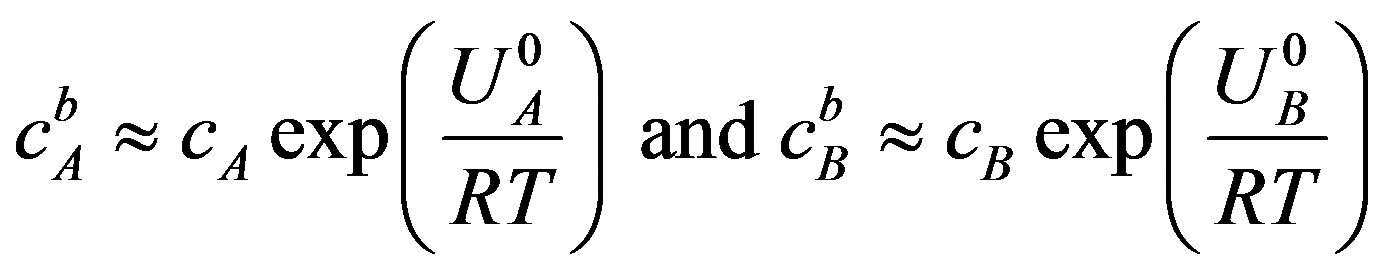 (20)
(20)
and therefore exert a drag pressure 
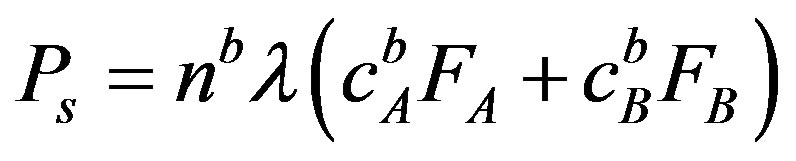 (21)
(21)
It should be noted that in their demonstration 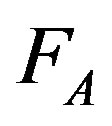 and
and  are not determined by the cusping of the boundary but by the Einstein’s equation
are not determined by the cusping of the boundary but by the Einstein’s equation
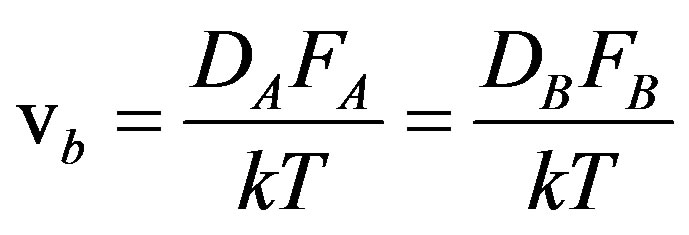 (22)
(22)
where  and
and 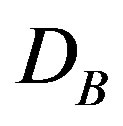 are the bulk diffusion coefficient of the solute atoms:
are the bulk diffusion coefficient of the solute atoms:
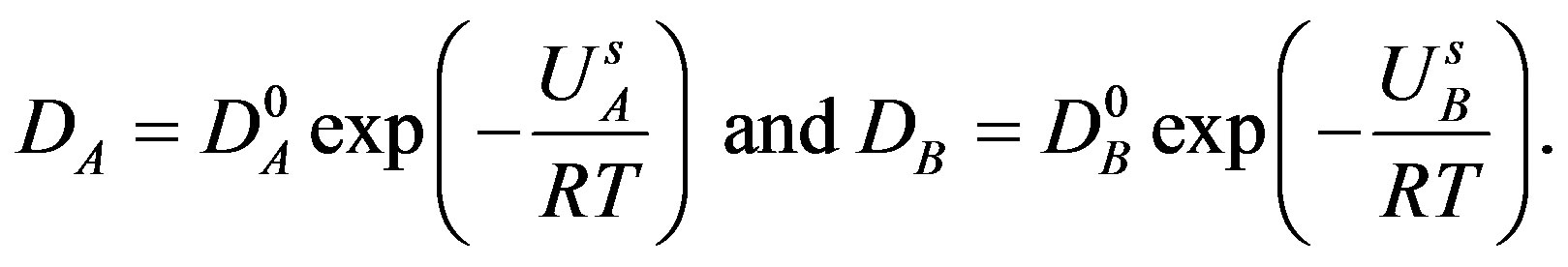
The boundary will move then with the velocity
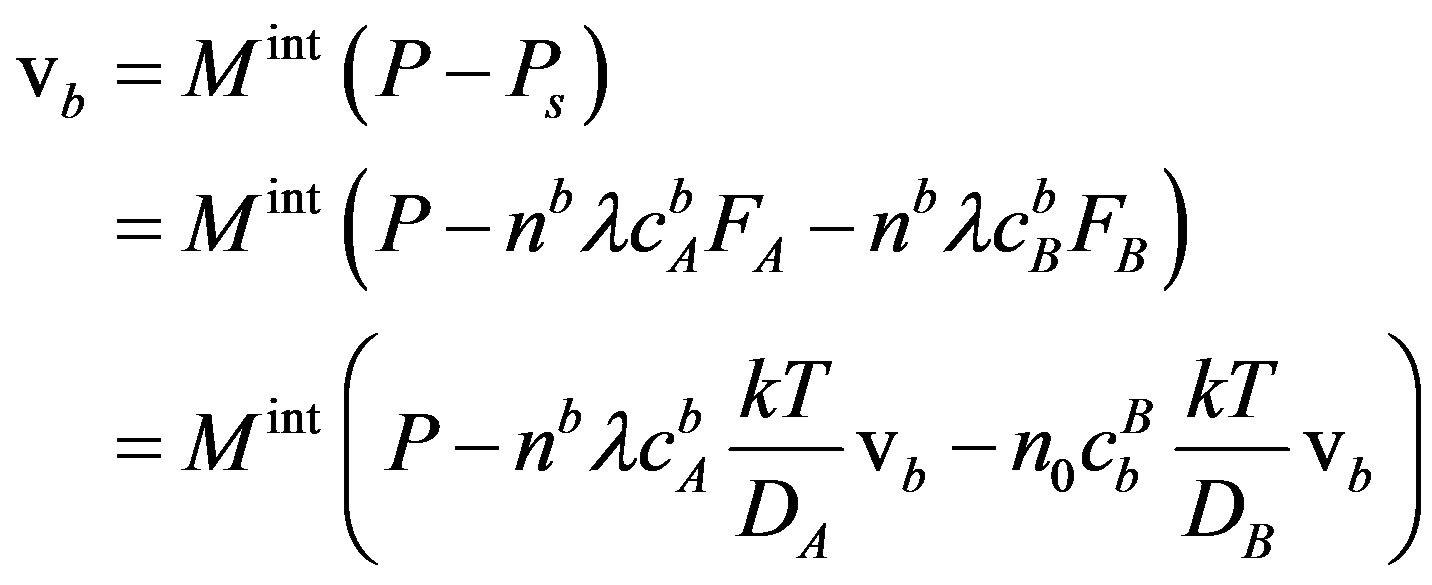 (23)
(23)
and therefore,
 (24)
(24)
In their approach, the quantities
 and
and
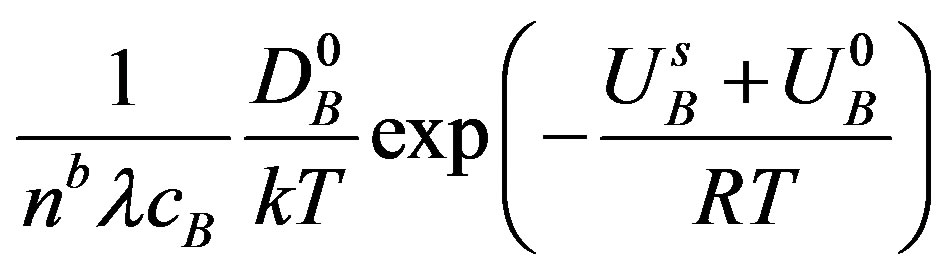 are respectively the mobility of the boundary when it is fully loaded either with solute atoms of type A
are respectively the mobility of the boundary when it is fully loaded either with solute atoms of type A 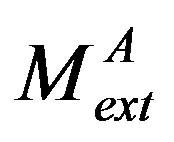 or B
or B . Finally, the boundary velocity could be expressed as
. Finally, the boundary velocity could be expressed as
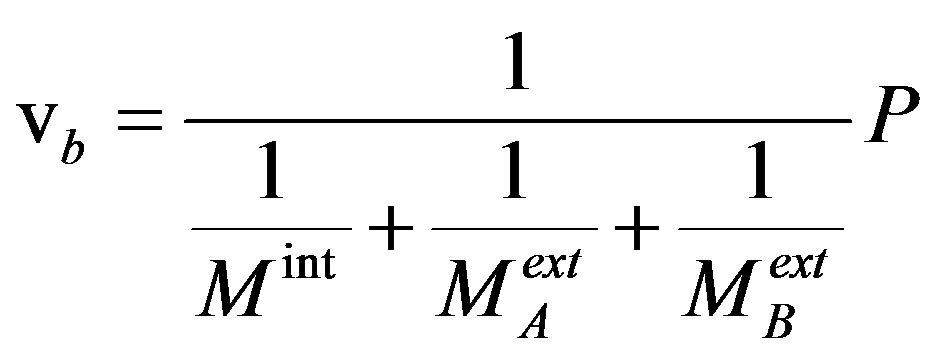 (25)
(25)
i.e. the same formula as the one in Equation (19), although the explicit expressions for the mobility terms are slightly different (see also [12]). The agreement between the solute cusping approach and the most accepted theory on solute drag can be understood by the fact that in the slow driving pressure/high solute content regime the solute cusping approach predicts a boundary which is nearly flat due to the large number of solute atoms pinning it [12], consistent with the original assumptions made by Lücke and Detert [14].
It is also interesting to note that a similar expression, although simpler, for solute drag effects in multi-component alloys was introduced as a phenomenological approach already by Vatne [15], to account for solute effects in the softening model Alsoft [16-18]. Here an effective concentration of solutes as derived from a summation of the solute concentration of the individual alloy elements, weighted by their activation energy for diffusion, is introduced into an equation analogous to Equation (11) [15].
However, although more stringently derived, it should be noted that some limitations also apply to the formula (Equations (19) and (25)). Firstly, interactions between the two types of solute have been neglected. The consequences of their interactions have been studied in [10,11]. Without considering site saturation in the boundary, it has been demonstrated that the solute drag in the presence of solute-solute interactions could either be increased or reduced depending on the nature of their interactions, attractive or repulsive [10]. It has also been proved that co-segregation of solutes competing for the boundary sites but not interacting with each other can lead to a complex behaviour where an impurity addition increases the boundary mobility [11]. Secondly, this formula only apply for the migration of a grain boundary in a dilute solid solution and do not tackle the problem of interphase migration into a multi-component system, which is at the time being out of the reach of this approach.
4. Conclusion
Despite the limitations mentioned before, and it still remains to be validated against real experiments, it is believed that the establishment of this formula (Equations (19) and (25)) has the potential of more accurate simulations of microstructure evolution (e.g. recrystallisation and sub-grain/grain growth) where solute drag effects are of importance, and thus in computer aided design of industrial processes and alloys. In particular, as compared to simpler approaches, it may be important in alloys where different solute has significantly different diffusion rates and/or boundary segregation tendencies (as expressed by the activation energy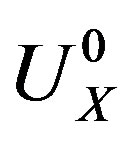 )
)
Acknowledgements
This research work has been supported by a KMB project (project number: 193179/I40), in Norway. The financial support by the Research Council of Norway and the industrial partners, Hydro Aluminium and Sapa Technology is gratefully acknowledged.
REFERENCES
- J. W. Cahn, “The Impurity-Drag Effect in Grain Boundary Motion,” Acta Metallurgica, Vol. 10, No. 9, 1962, pp. 768-798.
- K. Lücke and H. P. Stüwe, “On the Theory of Impurity Controlled Grain Boundary Motion,” Acta Metallurgica, Vol. 19, No. 10, 1971, pp. 1087-1099.
- J. Ågren, “A Simplified Treatment of the Transition from Diffusion Controlled to Diffusion-Less Growth,” Acta Metallurgica, Vol. 37, No. 1, 1989, pp. 181-189.
- M. Enomoto, “Influence of Solute Drag on the Growth of Proeutectoid Ferrite in Fe-C-Mn Alloy,” Acta Materialia, Vol. 47, No. 13, 1999, pp. 3533-3540.
- G. R. Purdy and Y. J. M. Brechet, “A Solute Drag Treatment of the Effects of Alloying Elements on the Rate of the Proeutectoid Ferrite Transformation in Steels,” Acta Metallurgica and Materialia, Vol. 43, No. 10, 1995, pp. 3763-3774.
- M. Hillert, “Solute Drag in Grain Boundary Migration and Phase Transformations,” Acta Materialia, Vol. 52, No. 18, 2004, pp. 5289-5293.
- J. Odqvist, B. Sundman and J. Ågren, “A General Method for Calculating Deviation from Local Equilibrium at Phase Interfaces,” Acta Materialia, Vol. 51, No. 4, 2003, pp. 1035-1043.
- J. Svoboda, E. Gamsjäger, F. D. Fischer and P. Fratzl, “Application of the Thermodynamic Extremal Principal to the Diffusional Phase Transformations,” Acta Materialia, Vol. 52, No. 4, 2004, pp. 959-967.
- J. Svoboda, J. Vala, E. Gamsjäger and F. D. Fischer, “A Thick-Interface Model for Diffusive and Massive Phase Transformation in Substitutional Alloys,” Acta Materialia, Vol. 54, No. 15, 2006, pp. 3953-3960.
- Y. J. M. Bréchet and G. R. Purdy, “Solute Drag in Ternary Solid Solutions,” Acta Materialia, Vol. 51, No. 18, 2003, pp. 5587-5592.
- M. I. Mendelev and D. J. Srolovitz, “Co-Segregation Effects on Boundary Migration,” Interface Science, Vol. 10, No. 2-3, 2002, pp. 191-199.
- E. Hersent, K. Marthinsen and E. Nes, “The Effect of Solute Atoms on Grain Boundary Migraton: A Solute Pinning Approach,” Metallurgical and Materials Transactions A, Vol. 44, No. 7, 2013, pp. 3364-3375.
- G. G. Gottstein and G. G. L. S. Shvindlerman, “Grain Boundary Migration in Metals: Thermodynamics, Kinetics, Applications,” 2nd Edition, CRC Press, Boca Raton, 2009.
- K. Lücke and K. Detert, “A Quantitative Theory of GrainBoundary Motion and Recrystallization in Metals in the Presence of Impurities,” Acta Metallurgica, Vol. 5, No. 11, 1957, pp. 628-637.
- H. E. Vatne, “Modelling the Evolution of Microstructure and Mechanical Properties during Back-Annealing of Rolled Sheets of AA3XXX Aluminium Alloys,” Proceedings of the 3rd International Conference on Modelling of Metal Rolling Processes, London, 13-15 December 1999, pp. 247-256.
- O. Engler, L. Löchte and J. Hirsch, “Through-Process Simulation of Texture and Properties during the Thermomechanical Processing of Aluminium Sheets,” Acta Materialia, Vol. 55, No. 16, 2007, pp. 5549-5463.
- J. A. Sæter, B. Forbord, H. E. Vatne and Erik Nes, “Modelling Recovery and Recrystallization; Applied to BackAnnealing of Aluminium Sheet Alloys,” Proceedings of the 6th International Conference on Aluminium Alloys, Toyohashi, 5-10 July 1998, pp. 113-126.
- H. E. Vatne, T. Furu, R. Ørsund and E. Nes, “Modelling Recrystallization after Hot Deformation of Aluminiumch,” Acta Materialia, Vol. 44, No. 11, 1996, pp. 4463-4473.

