Modeling and Numerical Simulation of Material Science
Vol.3 No.1(2013), Article ID:26900,5 pages DOI:10.4236/mnsms.2013.31002
Bonding Characteristics of TiC and TiN
1National Research Council Canada, Aerospace Portfolio, Ottawa, Canada
2Astronomy and Physics Department, Saint Mary’s University, Halifax, Canada
Email: *kuiying.chen@nrc-cnrc.gc.ca
Received July 28, 2012; revised September 3, 2012; accepted September 15, 2012
Keywords: Ab Initio Calculation; Chemical Bond; Electron Localized Function; TiC; TiN
ABSTRACT
Using ab initio density functional theory calculations, the electron localization function (ELF) of typical transition metal carbide TiC and nitride TiN were computed and analyzed to reveal their nature of the chemical bonds. The ELF approach was initially validated through typical examples of covalent-bonding Diamond (C) and ionic-bonding sodium chloride NaCl. Our results clearly demonstrate the dominantly ionic bonding characteristics of TiC and TiN. It is also suggested that the high mechanical hardness of TiC and TiN can be explained without evoking strong covalence.
1. Introduction
The mechanical, thermo-physical and dielectric properties exhibited by titanium carbide (TiC), titanium nitride (TiN) and similar titanium-metalloid (TiX) compounds, on the one hand, render the aforesaid substances appealing candidates for myriads of technological applications, and on the other hand, serve as motivation to a considerable number of investigations aiming at elucidating the nature of chemical bonds involved therein. Mechanical features such as high hardness and brittleness, and thermodynamic characteristics like high melting points are commonly believed to result from covalent bonding or some residual covalence in bonds of mixed nature. In contrast, the electric transport properties of TiX compounds evince sharp resemblance to metallic resistivity. In their exhaustive experimental studies of TiC and TiN bonds [1], Dunand and collaborators reported high resolution diffraction results exploited to generate charge density plots hinting at electron transfer from metallic s and d orbitals to nonmetallic p and s orbitals, and devoid of any trace of shared electronic clouds in the interstitial regions segregating the nuclei, as is the case with ionic bonds. In an early complementary density functional theory (DFT) base study of TiC and TiN bonding, however, Blaha and co-authors [2,3] suggested the possibility of a charge transfer due to orbital overlaps as an alternative mechanism pointing to covalent bonding. The latter proposition is adopted in the subsequent pieces of research, since it provides an explanation for the unusual mechanical and thermal properties of TiX compounds. In a more recent investigative endeavour [4], Mizuno and co-workers computed bond overlap population densities and densities of states for a host of TiX compounds (where X could be B, C, N, O, Si, P or S) using firstprinciple calculations with numerical atomic orbitals. Their results, although not indicative of notable overall covalence, are suggestive of “dominant covalency” in TiX bonds with the exception of Ti-O bonds. Despite the fact that most researchers acknowledge some ionic features in the Ti-X bonds, the generally accepted viewpoint categorizes TiC and TiN as either covalent materials or substances with mixed bonding characteristics.
In the present article, we shall expostulate that in both cases, the bonds are essentially ionic dominated and that this ionic character is capable of explaining the mechanical properties of TiC and TiN.
2. Theory
The electron localization function (ELF), which is inversely proportional to the square of the ratio of the kinetic energy of the system under study D and the kinetic energy characteristic of a homogeneous electron gas Dh to within an additive constant of unitary magnitude, gauges electron dispersiveness at position  [5]:
[5]:
 (1)
(1)
As can be seen from Equation (1), ELF equals 0.5 in the case of a metallic or jellium-like electron distribution and it approaches unity for highly localized electronic clouds. In the absence of significant electronic populations, ELF dwindles to nullity. The denominator of Equation (1), which depends on the kinetic energy, is related to the leading term in the Taylor expansion of conditional pair probability. As discussed by Becke and Edgecombe [6,7], the local value of ELF at position  indicates the probability of finding an electron at that locality given the existence of neighbouring electrons. Thus ELF provides a faithful and direct space depiction of electron distribution with no restrictions on the size or the type of the system to be probed [8]. The same kind of crude information can be extracted from charge density plots, where bond paths, nuclear sites, and cage structures as in benzene molecules are associated with the critical points of the dynamical system defined by the charge density gradient, i.e., saddle points, maxima and minima, respecttively. However, unlike ELF plots, the charge density plots do not always allow identifying the bonding nature in an unambiguous and unequivocal manner. This advantage of ELF is discussed in the literature in length in relation to the nature of intermetallic bonding [8,9] (The interested reader is particularly referred to reference 9, which discusses the information one can extract from ELF and charge density plots on aluminum bonds). Furthermore, substantial variations in charge density range from one system to another render quantitative comparative study of materials with inherently divergent bonding types complicated.
indicates the probability of finding an electron at that locality given the existence of neighbouring electrons. Thus ELF provides a faithful and direct space depiction of electron distribution with no restrictions on the size or the type of the system to be probed [8]. The same kind of crude information can be extracted from charge density plots, where bond paths, nuclear sites, and cage structures as in benzene molecules are associated with the critical points of the dynamical system defined by the charge density gradient, i.e., saddle points, maxima and minima, respecttively. However, unlike ELF plots, the charge density plots do not always allow identifying the bonding nature in an unambiguous and unequivocal manner. This advantage of ELF is discussed in the literature in length in relation to the nature of intermetallic bonding [8,9] (The interested reader is particularly referred to reference 9, which discusses the information one can extract from ELF and charge density plots on aluminum bonds). Furthermore, substantial variations in charge density range from one system to another render quantitative comparative study of materials with inherently divergent bonding types complicated.
Owing to the system independent limitedness of the range of its values, ELF can serve as a universal tool for fathoming the nature of chemical bonding across different compounds [8-10]. The universality and sharpness of ELF are evidenced in Figures 1 and 2 showing currently calculated electron distributions of sodium chloride NaCl and diamond. As displayed, the interstitial areas in NaCl are completely empty owing to the charge transfer characterizing ionic bonds, whilst the interionic regions in diamond are populated with shared electron pockets neighbouring the nonnuclear attractors, which constitute the hallmark of homopolar bonding. It is noteworthy to recall that the aforesaid plots essentially display the probability of localizing electrons in various positions and can thus corroborate valence population overlaps better than other indicators such as density of states or bond order indices. The authors successfully established conspicuous correspondence between ELF contour plots and Mayer’s bond order, which measures orbital overlap like Mulliken population overlap index, in an investigation illuminating the origins of the abnormally large shear modulus of iridium [11].
3. Ab Initio Method
In the present study, a super-cell model, Figure 3(a), was constructed to simulate B1 TiC (TiN). To evaluate the ELF, spin-polarized density functional theory calculations (DFT) were performed using the Vienna ab initio
 (a)
(a)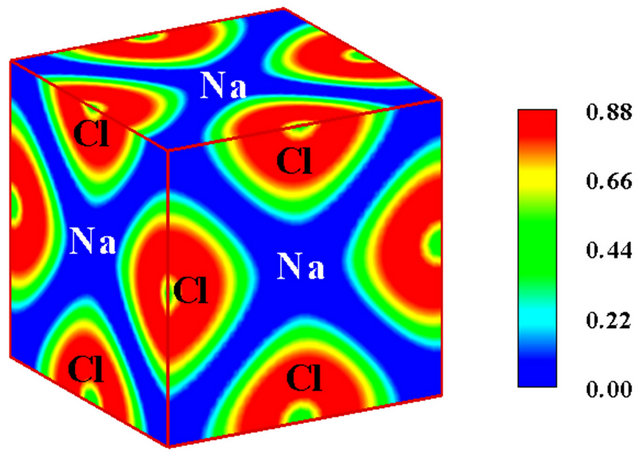 (b)
(b)
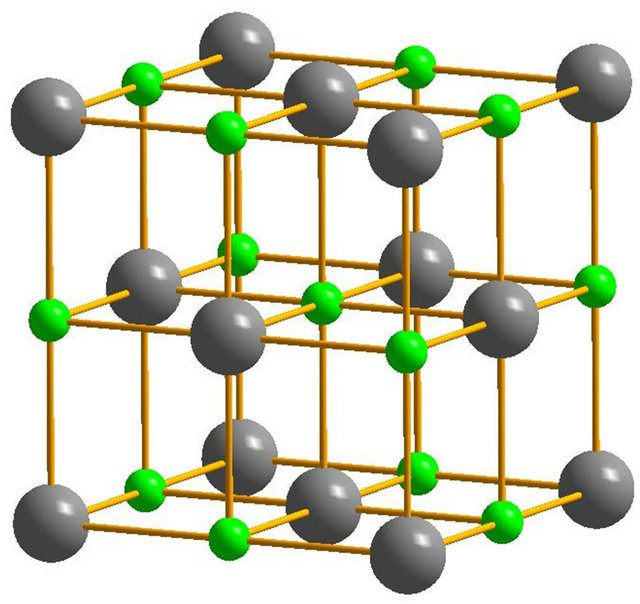
Figure 1. (a) The B1 unit cell model of NaCl. The grey solid spheres represent Na atoms, while the green spheres represent Cl atoms; (b) The electronic localized function of NaCl.
simulation package (VASP) within a plane-wave basis sets [12,13]. The Perdew-Wang generalized gradient approximation (GGA) was used to calculate the electron exchange and correlation energy [14,15]. The projector augmented wave (PAW) potentials were used to describe the interactions of valence electrons with the ion and core electrons for all elements [16]. The Brillouin zone integration was performed using a centered gamma point 11 × 11 × 11 Monkhorst Pack grid. The occupation of electronic states is determined according to the first order Methfessel-Paxton scheme with a smearing width of 0.2 eV. A kinetic energy cutoff of 350 eV is used for all total energy calculations. The unit cell of the model was fully relaxed during the calculation. The calculated lattice parameters for TiN and TiC were in a good agreement with experimental measurements and were published in our previous research [17,18].
4. Results and Analysis
In Figures 3(b) and (c), the three-dimensional ELF plots for TiN and TiC are displayed respectively. As can be seen, in both cases, no electronic cloud is observed in the interstitial regions, as the entire valence charge surrounds only the metalloid ions. It is therefore obvious that no internuclear pockets of shared electrons similar to bond
 (a)
(a) (b)
(b)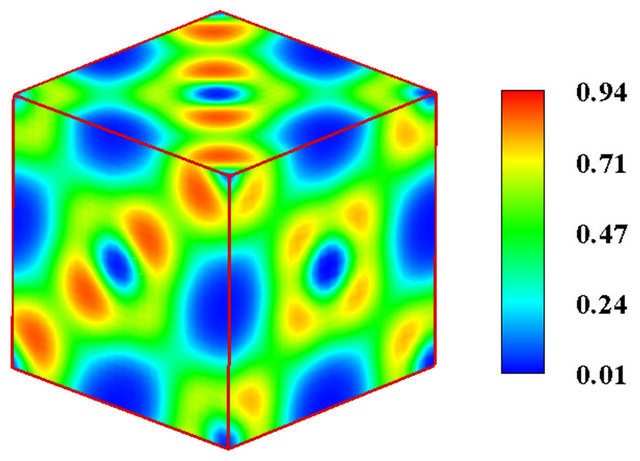 (c)
(c)
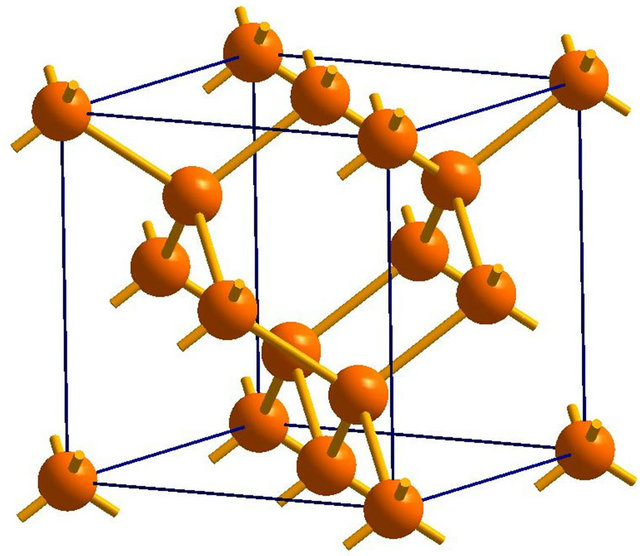
Figure 2. (a) The unit cell model of diamond; (b) The electronic localized function of diamond; (c) The electronic localized function of diamond.
populations detected in metallic and covalent crystals exist in these compounds. Moreover, residual charge overlaps appear solely between the non-metal ions and with low levels of localization since ELF assumes values smaller than 0.24 in all the cases. It is consequently untenable to ascribe any considerable degree of covalency to the TiX bonds as suggested by Mizuno and collaborators [4] or to attribute the thermo-physical properties of these compounds to the negligible covalency stemming from the homopolar interaction of metalloid nuclei. Furthermore all the characteristic features of ionic bonding as evinced in Figure 1 (valence charge transfer, absence of overlapping electron pockets along the bond paths etc) are present in TiC and TiN. It follows that the TiX bonds are essentially ionic and only minor covalency is per-
 (a)
(a) (b)
(b)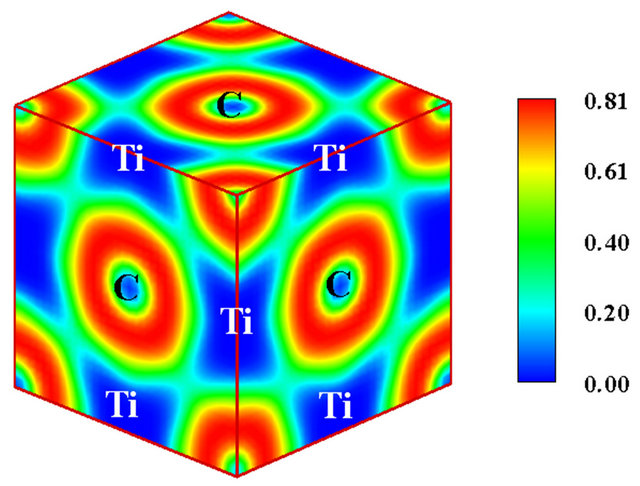 (c)
(c)
Figure 3. (a) The unit cell model of B1 TiC or TiN. The yellow spheres represent C or N atoms, while the blue spheres represent Ti atoms; (b) The calculate electronic localized function of TiN; (c) The calculated electronic localized function of TiC.
ceived between non-metal ions. It is worth mentioning that the association between covalency and brittleness, and large hardness is not a universal relation. For instance, compounds such as GaSb, GaAs or InSb and InAs, which evince rather low iconicity values (i.e., below 0.4) [19], do not exhibit any significant resistance to mechanical deformation [20]. Thus macroscopic features are not solely dictated by the nature of chemical bonding.
In a piece of investigation carried out by Clerc and Ledbetter [21], a universal semi-empirical formula for the mechanical hardness of well known covalent crystals such as C, BN and Si, and group II, III, IV and IV compounds, which include typical ionic materials such as NaCl, KCl and KI as well as TiC and TiN, was derived. Their formula relates mechanical hardness to the ratio of the nuclear charges, the surface state properties and the coordination number, and it predicts the mechanical hardness of all the aforesaid substances with reasonable accuracy. It thus ensues that the type of chemical bonding cannot be regarded as the primary parameter affecting mechanical hardness. Furthermore, their equation is a counterexample of the generally accepted association between covalency and large hardness, since their derivation is not based on any assumptions on the type of the bonding involved.
The evidence presented in previous investigations in support of the existence of noticeable covalency in TiC and TiN is primarily based on partial and total density of states DOS computed for different orbitals. Overlaps in partial orbital DOS constitute a well known indicator of hybridization, which may be interpreted as covalently shared electron pockets but the latter particular interprettation is not conclusive on its own. For instance, some researchers [4] claim that even Ti-O bonds in TiO2, which is firmly identified as an ionic compound, show some covalency because they exhibit p-orbital overlaps. Such interpretations of partial DOS are sometimes contradicted by charge density difference plots. It is noteworthy to mention that the ELF plots presented in the present paper faithfully reproduce the salient features of the experimental charge density difference plots obtained by Duvand and collaborators. It follows that even compared to DOS, ELF is a better tool at determining the nature of the chemical bonding at work without ambiguity.
The examination of total and partial DOS should carefully be carried out. The dispersion relation and the density of states reveal the band structure and hence the overlaps occurring between the bands, which are of pivotal importance in analyzing the electric transport properties of the compounds studied. The energetics of the systems is also determined from these relations and allows identifying the dominant chemical bonds; however, none of them can conclusively shed light on the very essence of the bonding created. Furthermore, concordance between orbital hybridisations detected from the DOS data and bond order indices is at first glance difficult to quantify and more importantly needs to be considered in relation to well-established ionic and covalent substances. For instance, it is hardly justifiable to regard bond order values nearing zero as serious evidence favouring covalency, when bond indices of typical covalent materials [22] approach unity or higher integers depending on the coordination number. The foregone discussion substantiates the accuracy and universality of ELF in delving the chemical bond and provides unequivocal evidence in support of the ionic nature of TiC and TiN bonds.
5. Conclusion
Within the frame of the current paper, results of ab initio DFT calculations are represented. The ELF three-dimensional direct space plots of TiC and TiN conspicuously demonstrate the ionic character of the dominant metal-metalloid bonds in these compounds. Our results also reinforce the fact that ELF, compared to bond order indices, partial and total DOS and charge density plots, is by far a better and universal tool for delving the essence of chemical bonding.
REFERENCES
- A. Dunand, H. D. Flack and K. Yon, “Bonding Study of TiC and TiN. I. High-Precision X-Ray Diffraction Determination of the Valence-Electron Density Distribution, Debye-Waller Temperature Factors, and Atomic Static Displacements in TiC0.94 and TiN0.99,” Physical Review B, Vol. 31, No. 4, 1985, pp. 2299-2315. doi:10.1103/PhysRevB.31.2299
- P. Blaha, J. Redinger and K. Schwarz, “Bonding Study of TiC and TiN. II. Theory,” Physical Review B, Vol. 31, No. 4, 1985, pp. 2316-2325. doi:10.1103/PhysRevB.31.2316
- K. Schwarz, “Band Structures and Chemical Bonding in Transition Metal Carbides and Nitrides,” Critical Reviews in Solid State and Materials Sciences, Vol. 13, No. 3, 1987, pp. 211-257. doi:10.1080/10408438708242178
- M. Mizuno, I. Tanaka and H. Adachi, “Chemical Bonding in Titanium Metalloid Compounds,” Physical Review B, Vol. 59, No. 23, 1999, pp. 15033-15047. doi:10.1103/PhysRevB.59.15033
- B. Silvi and A. Savin, “Classification of Chemical Bonds Based on Topological Analysis of Electron Localization Functions,” Nature, Vol. 371, No. 20, 1994, pp. 683-686. doi:10.1038/371683a0
- A. D. Becke, “Local Exchange-Correlation Approximations and First-Row Molecular Dissociation Energies,” International Journal of Quantum Chemistry, Vol. 27, No. 5, 1985, pp. 585-594. doi:10.1002/qua.560270507
- A. D. Becke and K. E. Edgecombe, “A Simple Measure of Electron Localization in Atomic and Molecular Systems,” Journal of Chemical Physics, Vol. 92, No. 9, 1990, p. 5397. doi:10.1063/1.458517
- B. Silvi and C. Gatti, “Direct Space Representation of the Metallic Bond,” Journal of Physical Chemistry A, Vol. 104, No. 5, 2000, pp. 947-953. doi:10.1021/jp992784c
- L. De Santis and R. Resta, “Electron Localization at Metal Surfaces,” Surface Science, Vol. 450, No. 1-2, 2000, pp. 126-132. doi:10.1016/S0039-6028(00)00057-1
- Q. Peng and S. De, “Tunable Band Gaps of Mono-Layer Hexagonal BNC Heterostructures,” Physica E, Vol. 44, No. 7-8, 2012, pp. 1662-1666. doi:10.1016/j.physe.2012.04.011
- S. Kamran, K. Chen, L. Chen and L. Zhao, “Electronic Origin of Anomalously High Shear Modulus and Intrinsic Brittleness of Fcc Ir,” Journal of Physics: Condensed Matter, Vol. 20, No. 8, 2008, Article ID: 085221. doi:10.1088/0953-8984/20/8/085221
- G. Kresse and J. Furthmũller, “Efficiency of ab Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set,” Computational Materials Science, Vol. 6, No. 1, 1996, pp. 15-50. doi:10.1016/0927-0256(96)00008-0
- G. Kresse and J. Furthmũller, “Efficient Iterative Schemes for ab Initio Total-Energy Calculations Using a PlaneWave Basis Set,” Physical Review B , Vol. 54, No. 16, 1996, Article ID: 11169. doi:10.1103/PhysRevB.54.11169
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, “Atoms, Molecules, Solids and Surfaces: Applications of the Generalized Gradient Approximation for Exchange and Correlation,” Physical Review B, Vol. 46, No. 11, 1992, pp. 6671-6687. doi:10.1103/PhysRevB.46.6671
- P. E. Blöchl, “Projector Augmented-Wave Method,” Physical Review B. Vol. 50, No. 24, 1994, pp. 17953-17979. doi:10.1103/PhysRevB.50.17953
- G. Kresse and D. Joubert, “From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method,” Physical Review B, Vol. 59, No. 3, 1999, pp. 1758-1775. doi:10.1103/PhysRevB.59.1758
- K. Chen, L Zhao, J. Rodgers and J. S. Tse, “Alloying Effects on Elastic Properties of TiN-Based Nitrides,” Journal of Physics D: Applied Physics, Vol. 36, No. 21, 2003, p. 2725. doi:10.1088/0022-3727/36/21/021
- K. Chen and L. Zhao, “Elastic Properties, Thermal Expansion Coefficients and Electronic Structures of Ti0.75X0.25C Carbides,” Journal of Physics and Chemistry of Solids, Vol. 68, No. 9, 2007, pp. 1805-1811. doi:10.1016/j.jpcs.2007.05.008
- J. C. Phillips, “Ionicity of the Chemical Bond in Crystals,” Reviews of Modern Physics, Vol. 42, No. 3, 1970, pp. 317-356. doi:10.1103/RevModPhys.42.317
- S. Kamran, K. Chen and L. Chen, “Semiempirical Formulae for Elastic Moduli and Brittleness of Diamondlike and Zinc-Blende Covalent Crystals,” Physical Review B, Vol. 77, No. 9, 2008, Article ID: 094109. doi:10.1103/PhysRevB.77.094109
- D. G. Clerc and H. M. Ledbetter, “Mechanical Hardness: Atomic-Level Calculations for Diamond-Like Materials,” Journal of Physical Chemistry A Solids, Vol. 59, No. 6-7, 1998, pp. 1071-1095. doi:10.1016/S0022-3697(97)00251-5
- I. Mayer, “Bond Orders and Valences from ab Initio Wave Functions,” International Journal of Quantum Chemistry, Vol. 29, No. 3, 1986, pp. 477-483. doi:10.1002/qua.560290320
NOTES
*Corresponding author.

