Journal of High Energy Physics, Gravitation and Cosmology
Vol.04 No.02(2018), Article ID:84103,26 pages
10.4236/jhepgc.2018.42018
How to Determine Initial Starting Time Step with an Initial Hubble Parameter H = 0 after Formation of Causal Structure Leading to Investigation of the Penrose Weyl Tensor Conjecture
Andrew Walcott Beckwith
Physics Department, College of Physics, Chongqing University, Huxi Campus, Chongqing, China

Copyright © 2018 by author and
Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International
License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: February 18, 2018; Accepted: April 24, 2018; Published: April 27, 2018
ABSTRACT
We start where we use an inflaton value due to use of a scale factor . Also we use as the variation of the time component of the metric tensor in Pre-Planckian Space-time. In doing so, what we lead up to using the Huang Superfluid universe model, which is by the modified superfluid cosmology model leading to examining within the Pre Planckian regime, Curvature, small but non zero, and energy density . The Potential energy is given by what it would be if leading to a relationship of , where we will isolate conditions for the initial time and compare them against a root finder procedure given in another paper written by the author. Then, afterwards, assuming a modified Hubble parameter, with an initial Hubble parameter after the Causal surface with, right after a quantum bounce, determined by , is then . And is an initial degree of freedom value of about 110. Then, the graviton production rate is a function of time leading to a temperature T dependence, with M here is a chosen Mass scale, M of about 30 TeV, with d greater than or equal to zero, representing the Kaluza Klein dimensions assumed with the number of gravitons produced after the onset of Causal structure given by . This by Infinite quantum statistics is proportional to entropy. We close with a caveat as far as the implications of all this to the Penrose Conjecture about the vanishing of the Weyl tensor, in the neighborhood of a cosmological initial singularity. And what we think should be put in place instead of the Penrose Weyl tensor hypothesis near a “cosmological” singularity. And we close with a comment about the Weyl curvature tensor, in Pre Planckian to Planckian physics, and also a final appendix on the Mach’s principle as written by Sciama, in defining the initial space-time non-singular “bubble”.
Keywords:
Inflaton Physics, Causal Structure Entropy, Temperature Dependent Initial Graviton Production, Kaluza Klein Dimensions, Penrose Weyl Tensor Conjecture

1. Referral to the Huang Superfluid Universe Model
Note that reference is made as to an assumed “Gyraton” as a candidate model, and this is for a particle which is assumed to have possibly a different character, in the Pre Planckian to Planckian transformation so alluded to in this document. [1] . Gyraton’s may be a way to generalize gravitons, which is a thought which will be brought up in future iterations as to this document.
The Gyration as a particle construct is given in [1] as an object that has a finite energy and spin, moving at the speed of light. i.e. conceivably, gravitons may be massless, in the initial phases of their existence, in the Pre Planckian era, and become with a designated mass. Hence, the construct in [1] is to generalize this particle, which is further explained in [2] .
But what we will do, is to clarify matters, is to assume an initial working mass energy value, as to Pre-Planckian to Planckian physics of about 30 TeV. As was asked by Corda, in private communications, as to the following question, “What are the physical reasons to choose a mass scale, M of about 30 TeV?” [3] , the reason this is picked, as a set point for a minimum amount of energy used to transmit “information” from a prior universe, to a present universe, as sufficient in itself to set the value of the Planck’s constant, h, as an invariant from universe to universe, to avoid the situation where there would be wildly varying physical laws, i.e. as a stabilization factor.
This same value of M, as 30 TeV will appear in subsequent places in the document.
This goes, then to the heart of the matter, which is how to obtain a working synthesis, of information exchange for the consistency of physical law, from prior to present universes.
In order to do this, we appeal also, to what was done by Ng [4] as “infinite quantum statistics” where there is a counting of emergent particles, i.e. entropy, which is referenced by Appendix A, i.e. the start of nucleated particles, which is in tandem, and also relevant to our constructions used by [5] , where an entropy counting protocol, is also a measure of information and computational steps, as designated by Lloyd in [5] .
But this does not fully explain the genesis of how and why we used Huang, in [6] as far as an initial embedding structure, i.e. one of the flawed mechanisms used to account for the onset of massive gravity is in [7] , i.e. the so called Vainshtein mechanism.
As stated in [7] :
Quote:
We introduce the Vainshtein mechanism which plays a crucial role in massive gravities, as well as in related theories such as Galileons and their extensions. This mechanism, also known as k-mouflage, allows to hide via non linear effects―typically for source distances smaller than a so-called Vainshtein radius which depends on the source and on the theory considered―some degrees of freedom whose effects are then only left important at large distances”.
i.e. our fundamental disagreement has to go with the caveat “some degrees of freedom whose effects are then only left important at large distances”. This is a huge fudge factor which we are trying to avoid.
The problem is stated here, i.e. in [7] :
Quote:
The simplest theory for a non self-interacting massive graviton is known as the Fierz-Pauli theory [8] [9] . It suffers from a pathology known as the vDVZ discontinuity [10] as will be introduced below. This is enough to rule out such a theory from basic solar system tests of gravity. However, soon after the discovery of the vDVZ discontinuity, a way out was suggested by Vainshtein [11] as well as [12] , relying on a non-linear extension of the Fierz-Pauli theory [11] [12] [13] .
End of quote.
We are motivated in the use of our model as to try to set up an analytical counterpart to [8] - [13] in our document, which will be due to our use of infinite quantum statistics, as outlined in Appendix A, [4] a way also to account for information for sufficient preservation of h bar from universe to universe, but in a way which is more precise, in eventual execution. Note that one of the popular embedding procedures as to what our universe, as a starting point, is referenced, to, is the popular Kaluza-Klein supposition, i.e. built around the idea of a fifth dimension beyond the usual four dimensions of space and time [14] [15] [16] [17] .
We view this as very important, but we are offering a different way as to perform an embedding of space-time.
This is also different from the Randall Sundrum model, which we summarize in Appendix B which involves references [18] and [19] .
A fifth dimensional representation of the ideas involved can be found, in a different venue in [20] , by t’Hooft in his paper, where he appeals to a deterministic embedding structure for Quantum mechanics, which we think in spirit is akin to, with caveats to Appendix B.
This is fine if we are not worried as to consistency of physical law, and we are, hence, we appeal to [6] as a data match up to an earlier space time bubble.
But, in order to do it, we need a regime of space-time, which will permit the start of nucleation of our present universe. Our candidate for doing such is given by Huang [6] whom we explain below, in terms of what is a “super fluid” universe, which is at the start of a causal boundary of space-time.
We look at [6] by Huang, as to a critical density affecting scale factor “size of the universe” as given by
(1)
This curvature, in the vicinity of Pre-Planckian space-time is of minimal value. Whereas Huang delineates the evolution of the scale factor as [6]
(2)
The scalar field which Huang accesses is , with this being due to setting V as dependent upon the Kummel function, as written up in page 58 of [6] with, here, n going from 1 to N, in terms of scalar fields, and
(3)
As given by [6] , this potential system is from one loop Feynman diagrams as given in [21] . Our approximation is to set N as equal to 1, in the Pre Planckian regime, with the Causal structure creation zone, at the “bubble” of space-time leading to a bifurcation of additional structure and additional space-time scalar fields, as delineated by . However before this happens to delineate the initial scalar field, with N = 1 as within the bubble of space-time. What we are doing is to review what was put in [22] and contrast it to a (single field?) version of Equation (3) above. In doing so we are using the Padmanbhan treatment of the linkage between scale factor, inflaton, and what was done in [22] while assuming that the Equations ((4) and (5)) is for the regime of the quantum bubble, possibly of radii Plank length, and then match it to Equation (3) above. i.e. probably of Planck dimensions, as having [22] .
We will remark upon utilization of the following two scalar potentials and the potential system in the following manner. In Equation (3) we explicitly refer to a multi scalar inflaton field, which we can all as with values from 1 to N. But in the pre Planckian regime, we are looking at a single inflaton field version of the dynamics, which is given in Equation (5) below.
In this case, the dynamics of our problem will be laid out as follows
(4)
The first stage of this evolution, is given by Equation (4) below. The Second stage has the scalar field as given in as stated for Equation (4) below, but then mapped as the first admitted scalar field as given in Equation (3), and then the final stage, has scalar fields which can be ranging from 1 to N in labels, which would be a physical transformation of the problem from a single field regime, to a multi scalar field regime, with similarities to super fluid helium.
In Appendix C, we argue that this is similar to a particle in a quantum state, in a box, when the box is then suddenly opened up. i.e. in that quantum experiment which is in Appendix A, we have a ground state probability of P(1) = 0.41 that a ground state wave function would be n = 1 and stay there if the length of the box were changed from L/2 to L, and we argue that we have an analogous situation here, for the linkage given for Equations (3)-(5) given here. Having said that let us look at the Pre Planckian inflaton field, which motivates the start of our analysis.
The idea is to have a split between a Pre Plank single valued inflaton field, and a multi valued Planckian inflation field. In addition, this transition between the Pre Planckian to Planckian space-times will initiate as we view it, primordial graviton production.
In short a single inflaton field will dominate the interior of an inflaton bubble, and then be considered as bridged to a single field version of Equation (3) above initially. i.e. the single field inflaton, will obey the relations which were cited as given in [22] which we reproduce below as
(5)
To employ this Equation (5) we are using, as was done in [22] , the following boundary condition of the bubble of Space-time as was given in [22] which we put in as being the boundary of a purported quantum bounce. This is also substantially using [23] which using the material so cited.
In doing this, we also can state that there is a commensurate internal wave function, within this bubble. We will allude to this later. See the conclusion.
Note that this all has profound linkage to the Penrose suggestion that the Weyl tensor vanishes at an initially assumed singularities of space-time. As given in [24] /i.e. the Penrose suggestion in [24] is that an “effective Weyl Curvature of a given frequency and amplitude allegedly adds an effective “gravitational energy” contribution to the Ricci Tensor of magnitude of the square of the amplitude of the Weyl tensor, times 1 over the frequency of the alleged Weyl tensor oscillatory frequency, squared.
Penrose suggestion leads to the suggestion that if the amplitude of the Weyl tensor is zero, then there would be no “gravitational energy”.
We suggest here, that the Weyl tensor would NOT vanish, if our formulas Equations (3)-(5) hold, and that instead there would be gravitational energy. In Appendix C, we examine some quantum mechanical arguments as to our problem, at the boundary of a nonsingular initial bubble of space-time, and in Appendix D, we will examine and amplify what we mean as to the consequences of Gravitational potential energy. i.e. in doing so, we cite a different interpretation of [24] as given, as a way confirming the existence of initial non zero entropy at the start of cosmological expansion.
Note that we have in our document access to looking at the interior of the presumed initial space-time bubble of Pre Causal space time. This will be in lieu of [25] [26] and [27] which yields us Equation (6) below
(6)
The n = N version would have ONE component of the potential largely dominated by the Equation (4) write up, and the rest of the structure would be additional according to the Kummel potential write up as given in Equation (1) given above.
From now on, we will be examining the physics implications of finding and using Dt.
2. Examining Dt from the Vantage Point of a Minimum Scale Factor Calculation
To do this, we have that interpretation of Equation (1) will lead to the following linkage of scale factor of the Universe, minimum, and the time derivative of the inflaton field, as given in Equation (5) for the Pre Planckian regime, about the Causal structure as given in Equation (6) above, mainly, then
(7)
This is for a minimum time step, t, which in our re write is, then
(8)
What we are doing is to contrast different ways of obtaining a time step Dt and then employing the tools used in [22] and [23] . This also will be assuming [27] , as a given for analysis.
Then making use of [28] while using the tools given in reference [27] with is an initial degrees of freedom value of about 110 [29] , and T in Equation (8) as a temperature, right after the formation of Causal structure, and with M here is a chosen Mass scale, M of about 30 TeV [30] we find that Equation (9) below as given then will lead to via use of the ideas of [28] used again and again.
(9)
Note that we will in due course, also amplify this results linkage to Appendix D, in our conclusion.
Implying for a value right at the causal boundary of space time, i.e. the bounce radii of emergent
(10)
This will, if we utilize [27] tie in with a graviton production expression we give as, if d is the extra dimensions of assumed Kaluza-Klein space-time
(11)
As stated before, this assumes, that Equation (10) is by Ng. Infinite quantum statistics [31] , an entropy count, with at the Causal boundary, a nonzero value, in line with [13] [32] . And the non-zero value of the scale factor is largely in tune with the ideas of quantum bounces as given in Loop quantum gravity [14] [33] and also the nonlinear electrodynamic suggestions given by Camera [34] .
Having said that, we will then cite a result as given in [16] which involves a nonlinear equation for the Dt values used in Equations ((7) and (9)) which in turn affects Equation (10) which by infinite quantum statistics [31] implies that at a causal surface boundary, that we do not have non zero entropy.
3. Examination of the Minimum Time Step, in Pre-Planckian Space-Time as a Root of a Polynomial Equation
We initiate our work, citing [35] to the effect that we have a polynomial equation for the formation of a root finding procedure for Dt, namely if
(12)
From here, we then cited, in [34] using [31] a criteria as to formation of entropy, i.e. If L is an invariant cosmological “constant” and if Equation (12) holds, we can use the existence of nonzero initial entropy as the formation point of an arrow of time. given in Equation (1) with a counting algorithm of created gravitons giving a nonzero entropy which can also be cited as similar to the Entropy given below Note that this is the boundary between the single inflaton treatment given in Equation (5) and the more general equation
(13)
This should be compared with Equation (11) as a nonzero value for initial entropy at a causal surface/boundary.
Note that the most likely result of a solution for Equation (12) would be in the case that
(14)
What Equation (13) gives us then is an estimate as to a truncated value of time step which is tied into the arrow of time consideration as to the later part of this document. This is also linked to the causal barrier idea also alluded to in this document.
All this leads to a conclusion which is to the inter connectivity of initial conditions and nonzero entropy.
4. Conclusions: Inter Connection between Minimum Scale Factor, Dt and Equation (10). Much More to Explore
That there may be a linkage between a minimum scale factor, a minimum time step and initial graviton production is nothing other than stunning. Also, this can be linked to possible falsification of a prior suggestion brought up in [35] which we cite below. Can we also, in all of this, examine if there is an invariant cosmological constant, or if it varies with an initial electromagnetic field, as is suggested next?
One way to look at it would be to suggest that as done by H. Kadlecova [36] in the 12 Marcel Grossman meeting that the typical energy stress tensor, using, instead, Gyratons, [1] [2] with an electro-magnetic energy density addition to effective Electromagnetic cosmological value as given by
(15)
i.e. that there be, due to effective E and M field a boost from an initially low vacuum energy to a higher ones, as given by Kadlecova [36] [37]
(16)
If true, this may affect Equation (12) as given in the text. In addition we also should keep in mind the issues brought up by Abbot et al. and Corda, as far as foundational gravity as cited in [38] [39] [40] as well, i.e. parsing correctly would entail understanding the foundations of experimental gravity.
Finally, and not least, this construction of a single field, inflaton field, as given up to the Causal structure boundary is, if it is done correctly, probably linked to one of the many post causal inflaton fields, as referenced in [1] , and Eqution (1) of this presentation. The transition from one to possibly many inflaton fields, and a super fluid model of the universe be a way, as the author visualizes, of initiating turbulence at the start of the formation of a causal structure, with an analogy to superfluid induced turbulence as alluded to in [1] [6] . The author will explore a topic later. And also if we can observe the following generated GW, as given with defined Frequency
(17)
This frequency is in part due to the following argument as given by [40] as far as the article by Hallowell, as far as quantum cosmology [41] , as far as the interior wave function for the wave function in the interior of the bubble of space time, closely matched to the causal surface of the one Planck length radii of initial space-time. We then get an interior, no boundary wave functional of the form
(18)
This is an interior, no boundary condition for an interior wave functional as given by [41] and the important question to ask is how to match this WKB argument with the physics as represented by Eqution (17) above, as in sync with [42] .
If so, is this idea in sync with cyclic conformal cosmology [42] ?
One of the open questions this also leads to, is, if [42] , in terms of the cyclic conformal cosmology of Penrose is admissible, with this construction or is ruled out.
What we are also considering is, although not explicitly stated, a similar mechanism as is given in the Higgs formation of mass as is written up in page 480 to page 483 of [43] , and also a way to a possible linkage to [44] in terms of gravitons, and Higgs theory. In particular:
Quote:
Higgs mechanism at the graviton level as a consequence of the Vainshtein mechanism,
End of quote.
From [24] [44] may be developed in a future update of this document. Another alternative, to consider, in this temperature dependent regime, is also given by [25] [45] .
One final consideration. In [45] Oda has a rendering of the Cosmological Constant as given by the paragraph right after equation (42) of [45] .
Quote
Where the cosmological constant takes the form Λ = (2 − (5/4) times D) times m2, which is negative for D > 1. We conjecture that in this class of potentials, the cosmological constant might be always negative since the’t Hooft model belongs to this class.
End of quote
The radical suggestion the author has, that in the Pre Planckian regime, in the regime right next, or included within the bubble, that the effective spatial dimension, D, would be 1, i.e. a dramatic reduction of effective “dimensionality” with the effect that in the Pre-Planckian space-time, that one has, due to this, an effective POSITIVE cosmological constant. i.e. that the Oda conjecture applied literally should be with respect to the nucleated bubble of Pre Planckian space-time.
The author welcomes disagreements with this conjecture, and also wishes constructive engagement as to this point from interested readers.
We also wish to point to a recent paper, by Canate, Jime, and Salgado [46] as to the question if Geometric hair, in black hole theory is supported. by analytical and geometric models. The authors refer to several modified gravity models which impact the expansion of the universe. Minding that the Corda suggestion [39] as to how early universe models as to Tensor-Scalar models influence what is known about early universe experimental gravity data sets which could be expected, the additional benefit of our analysis, may be in helping to delineate what modified gravity models are admissible as far as the early universe, which in turn will directly impact the characterization of if or not black holes, indeed have geometric hair. If we go in addition to this, a review of [47] , where the author did a thought experiment as to what a causal discontinuity did as to the available fluctuations, and [48] on an inquiry as to if extra dimensions are necessary at all, and [49] as to how certain black hole results may be replicated, as far as the question of entanglement entropy in the early universe, we find that the model so given above, may have some very unexpected inter relationships with black hole physics, but also with the early universe at the same time.
Finally in a reminder as to purported bridges between the pre Planckian bubble, as would be for the physics, of linkage between Equtions ((3) and (4)) the author wishes to reiterate the following points.
Equation (4) in Pre Planckian physics up to a causal barrier, would be for a single field inflaton. The author is stating that the INITIAL inflaton field, if the causal structure structure is linked to the forming of Equation (3) by assuming that the Equation (4) construction would go to N = 1 of Equation (3). This would be equivalent, with the other inflaton fields, N = 2 to N = N, being filled out at the same time the physics of [47] was fulfilled.
The details of this would be in some respects also similar to a 2nd order phase transition. [49] Which is a point which will require additional modeling, that is the transition from N = 1 initial scalar field potential, to many scalar field potentials. We state unequivocally though that the details would have some overlap with the ideas outlined in [48] as to the quark gluon plasma and electroweak, but would not have the convenient simple phase diagrams as outlined in [50] . And then using Equations ((4) and (C2)) of APPENDIX C, below, we argue we then will have a probability of the suddenly liberated from just n = 1 ground state, of what we were looking at the causal barrier to be, that instead we will have a probability of P(1) ~ 0.41, as given by approximation in Appendix A, that the single field inflaton would be held to, in main value, with a 59 - 60 per cent probability that other inflaton states would be evolved to, as implied by [31] [51] . The exact particulars of this would be in refinement of an argument as qualitatively alluded to in [31] [51] below, with major refinements. Further elaborations are consistent with the ideas as given by Penrose in [52] .
We close with our arguments for further investigation of the results of Appendix D, which suggests that if there is not a Singularity, that there exists contributions to “gravitational energy” as cited on page 615 of [24] . If we conflate gravitational Gravitational Energy, with production of gravitons, and we use the Ng hypothesis [31] of infinite quantum statistics, to conflate a production of relic gravitons with a count of entropy, what we are suggesting is that our non-singular results for starting expansion are in tandem, due to [24] with nonzero initial entropy. Which would have profound observational data consequences.
Our final goal in this document, is to eventually come up with a detailed pre-Planckian physics analysis of a precursor to redoing the presumed Weyl cosmological tensor, and to in part modify [24] in terms of conclusions, relic gravitational energy at the start of cosmological expansion, and if [31] holds as far as gravitons, come up with a detailed analysis as to why the initial expansion of the universe starts off with nonzero entropy.
That will be the conclusion which we hope to reach in a future document. And this will by necessity, be reviewing Equations ((4), (5) and (18)) of our document as well as a re do of the assumed conclusions given in [24] as written up by Penrose, in 1978-1979.
It also requires a further elaboration of Equation (14) as well, which we intend to do in a future document which will also relate the discussion to the future projects alluded to in Appendix D.
We also will consider, in Appendix E, what the Weyl tensor, for at least 4 dimensions concludes as far as the Friedman-Walker-Lemaitre “perfect fluid” cosmology pertains to, with a comment in it as far as what the Pre Planckian to Planckian transition would say as far as the Penrose conjecture.
The tale away in Appendix E is that Equation (E1) has its simplified form, right after the Causal boundary, but that we would have to consider the transformations needed from Pre Planckian space time to Planckian, in order to come up with full analytical development as far as fi the Penrose Weyl tensor would indeed lead to a vanishing behavior at near singular conditions.
The development of this would be tied into fuller development of the point raised in Appendix D in a future publication. In addition, we also will make reference, to Appendix F, i.e. Where we have Mach’s principle as, in defining the initial space-time non-singular “bubble”. If, here, τ is a time unit, which is interpreted slightly differently than being the Hubble time, but instead is the recounting is given as
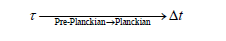 (19)
(19)
Whereas we will be interpreting
 (20)
(20)
The discussion of the applications of Equations ((19) and (20)) are linked with suitable references, and also are tied, into an interpretation of Equation (4) in a way which introduces the idea of quantum mechanics being introduced, near the causal boundary surface as referenced in Equation (14) in a way which makes our interpretation of space-time gravitational wave signals being produced, also, in effect, linked to when holds, in effect transforming it to a data set we will call
 (21)
(21)
This is our final future works project which we will attempt to confirm or to analyze via future data sets, and we will do it while asserting that Dt is tied into a solution to Equation (12).
All these suppositions, plus the idea of when we go from Quantum to quasi- classical will be extended from Appendix D, and will be hopefully made congruence with respect to Appendix B, as far as the Weyl conjecture by Penrose, as well as also giving more explicit content to Appendix E, as far as the transition from one inflaton field, to perhaps many inflaton fields. With the initial inflaton field being approximately 41% of being one of the many past the causal boundary multiple inflaton fields. i.e. this transformation, as alluded to in Equation (4) will be in its end product the graviton/gravitational wave generation of our model, and deserves further future elaboration.
In doing so, the author wishes to add another experimental bench mark to review, namely that one has a mass of the graviton, at near light speed being greater than the presumed rest mass of the “massive” graviton, which would be a staggering increase in the effective mass of gravitons, traveling near the speed of light, right after the H = 0 causal boundary surface.
The further explanation of this business is in Appendix F, and would be important in itself as far as to ascertain the fidelity of GW data sets, with the predictions of [38] [39] [40] .
In itself this would be lending toward trying to ascertain experimental data set confirmation if this is viable and a reasonable datum to consider in this situation. As a datum which may explain the black hole situation where the mass of a graviton, should it exist, have a Compton wavelength greater than the GW wave fronts ascertained in the LIGO measurements, as well as other issues, in [19] [20] [53] .
In doing all of this, we urge the readers to keep in mind earlier work done by the author as to a Modified Heisenberg Uncertainty principle, which is summarized in Appendix G. All of what we have here should be summarized and compared to a result which is to be held in sync with the physics of Pre Planckian to Planckian physics as outlined below. It goes without saying that a major task of our future work should be comparing the results of Equations ((1) to (4)) of our main document with the modified Heisenberg Uncertainty principle, in Appendix E. Also, and not least will be in doing further computational matching of our presumed Causal boundary, as given of about Planck Length in radii, as the pre Planckian to Planckian physics, boundary with the requirements of the Mach’s principle, as given in Appendix C, Appendix E, and Appendix F.
We will, also, in doing it refer to Appendix H, as far as adding brief commentary as to the generation of Gravitational waves, due to the split between Pre Planckian single valued inflaton structure, and Planckian multiple valued inflaton structure. This will be aided later on by full use of the material in Appendix G.
This will be all part of an update later as far as actual details as to the Weyl tensor behavior near the quantum bubble regime as opposed to what we could expect if we had an actual physical singularity.
Acknowledgements
This work is supported in part by National Nature Science Foundation of China grant No. 1137527.
Cite this paper
Beckwith, A.W. (2018) How to Determine Initial Starting Time Step with an Initial Hubble Parameter H = 0 after Formation of Causal Structure Leading to Investigation of the Penrose Weyl Tensor Conjecture. Journal of High Energy Physics, Gravitation and Cosmology, 4, 236-261. https://doi.org/10.4236/jhepgc.2018.42018
References
- 1. Kadlecová, H. and Krtous, P. (2014) The Gyraton Solutions on Generalized Melvin Universe with Cosmological Constant. Workshops on Black Holes and Neutron Stars 2008/2009/2010/2011, Silesian University in Opava, 61-74. https://arxiv.org/abs/1610.08225
- 2. Kadlecova, H., Zelnikov, A., Krtous, P. and Podolsky J. (2009) Gyratons on Direct-Product Spacetimes. Physical Review D, 80, Article ID: 024004. https://arxiv.org/abs/0905.2476
- 3. Corda, C. (2016) Question Brought to the Attention of the Author, Which Is Answered in the Initial Part of the Document.
- 4. Ng, Y. (2008) Spacetime Foam: From Entropy and Holography to Infinite Statistics and Nonlocality. Entropy, 10, 441-461. https://doi.org/10.3390/e10040441
- 5. Lloyd, S. (2002) Computational Capacity of the Universe. Physical Review Letters, 88, Article ID: 237901. https://arxiv.org/abs/quant-ph/0110141
- 6. Huang, K. (2017) A Superfluid Universe. World Scientific, Singapore.
- 7. Babichev, E. and Deffayet, C. (2013) An Introduction to the Vainshtein Mechanism. Classical and Quantum Gravity, 30, Article ID: 184001. https://arxiv.org/abs/1304.7240 https://doi.org/10.1088/0264-9381/30/18/184001
- 8. Harvey, A. and Schucking, E. (2000) Einstein’s Mistake and the Cosmological Constant. American Journal of Physics, 68, 723. https://doi.org/10.1088/0264-9381/30/18/184001
- 9. Pauli, W. and Fierz, M. (1939) Uber die relativistische Theorie kräftefreier Teilchen mit beliebigem Spin. Helvetica Physica Acta, 12, 297.
- 10. Fierz, M. and Pauli, W. (1939) On Relativistic Wave Equations for Particles of Arbitrary Spin in an Electromagnetic Field. Proceedings of the Royal Society A, 173, 211. https://doi.org/10.1098/rspa.1939.0140
- 11. van Dam, H. and Veltman, M.J.G. (1970) Massive and Mass-Less Yang-Mills and Gravitational Fields. Nuclear Physics B, 22, 397-411. https://doi.org/10.1016/0550-3213(70)90416-5
- 12. Zakharov, V.I. (1970) Linearized Gravitation Theory and the Graviton Mass. JETP Letters, 12, 312.
- 13. Vainshtein, A.I. (1972) To the Problem of Nonvanishing Gravitation Mass. Physics Letters B, 39, 393-394. https://doi.org/10.1016/0370-2693(72)90147-5
- 14. Kaluza, T. (1921) Zum Unitätsproblem in der Physik. Preuss. Akad. Wiss. Berlin. Math. Phys., 33, 966-972.
- 15. Klein, O. (1926) Quantentheorie und fünfdimensionale Relativitütstheorie. Zeitschrift für Physik, 37, 895-906. https://doi.org/10.1007/BF01397481
- 16. Klein, O. (1926) The Atomicity of Electricity as a Quantum Theory Law. Nature, 118, 516. https://doi.org/10.1038/118516a0
- 17. Wesson, P.S. and Ponce de Leon, J. (1995) The Equation of Motion in Kaluza-Klein Cosmology and Its Implications for Astrophysics. Astronomy and Astrophysics, 294, 1-7.
- 18. Sundrum, R. (2005) Extra Dimensions. SLAC Summer Institute: Gravity in the Quantum World and the Cosmos. http://www-conf.slac.stanford.edu/ssi/2005/program.htm
- 19. Beckwith, A.W. How a Randall-Sundrum Brane-World Effective Potential Influences Inflation Physics. https://arxiv.org/ftp/physics/papers/0610/0610247.pdf
- 20. Hooft, G. (1999) Quantum Gravity as a Dissipative Deterministic System. Classical and Quantum Gravity, 16, 3263-3279. https://doi.org/10.1088/0264-9381/16/10/316
- 21. Halpern, J.K. and Huang, K. (1996)
- 22. Padmanabhan, T. (2005) Understanding Our Universe: Current Status and Open Issues. In: Ashtekar, A., Ed., 100 Years of Relativity—Space-Time, Structure: Einstein and Beyond, World Scientific, Singapore, 175-204. http://arxiv.org/abs/gr-qc/0503107
- 23. Beckwith, A. (2017) Constraints, in Pre-Planckian Space-Time via Padmabhan’s Λinitial·H-2initial≈o (1) Approximation Leading to Initial Inflaton Constraints and Its Relation to Early Universe Graviton Production. Journal of High Energy Physics, Gravitation and Cosmology, 3, 322-327. https://doi.org/10.4236/jhepgc.2017.32027
- 24. Roger, P. (1979) Singularities and Time-Asymmetry. In: Hawking, S. and Israel, W., Eds., General Relativity, an Einstein Centenary Survey, Cambridge University Press, Cambridge, UK, 581-638.
- 25. Beckwith, A. (2016) Gedanken Experiment for Refining the Unruh Metric Tensor Uncertainty Principle via Schwarzschild Geometry and Planckian Space-Time with Initial Nonzero Entropy and Applying the Riemannian-Penrose Inequality and Initial Kinetic Energy for a Lower Bound to Graviton Mass (Massive Gravity). Journal of High Energy Physics, Gravitation and Cosmology, 2, 106-124. https://doi.org/10.4236/jhepgc.2016.21012
- 26. Giovanni, M. (2008) A Primer on the Physics of the Cosmic Microwave Background. World Press Scientific, Hackensack, New Jersey. https://doi.org/10.1142/6730
- 27. Dowker, F. (2005) Causal Sets and the Deep Structure of Spacetime. https://arxiv.org/abs/gr-qc/0508109
- 28. Sarkar, U. (2008) Particle and Astro Particle Physics. In: Series in High Energy Physics and Gravitation, Taylor & Francis, New York.
- 29. Kolb, E. and Turner, M. (1991) The Early Universe. Westview Frontiers in Physics Series, Vol. 69.
- 30. Rubakov, V. (2001) Large and Infinite Extra Dimensions. Physics-Uspekhi, 44, 871-893. https://arxiv.org/abs/hep-ph/0104152
- 31. Ng, Y.J. (2007) Holographic Foam, Dark Energy and Infinite Statistics. Physics Letters B, 657, 10-14. https://doi.org/10.1016/j.physletb.2007.09.052
- 32. Keifer, C. (2012) Can the Arrow of Time Be Understood from Quantum Cosmology? In: Mersini-Houghton, L. and Vaas, R., Eds., The Arrows of Time: A Debate in Cosmology, Fundamental Theories in Physics, Springer, Heidelberg, Vol. 172, 191-203.
- 33. Rovelli, C. and Vidotto, F. (2015) Covariant Loop Quantum Gravity. Cambridge University Press, Cambridge, UK.
- 34. Camara, C.S., de Garcia Maia, M.R., Carvalho, J.C. and Lima, J.A.S. (2004) Nonsingular FRW Cosmology and Non Linear Electrodynamics. Physical Review Journals, 69, Article ID: 123504.
- 35. Beckwith, A. (2017) How a Minimum Time Step Based in Pre Planckian Space-Time If Friedman Equation H Set Equal to Zero Leads to the Arrow of Time. http://vixra.org/abs/1702.0290
- 36. Kadlecova, H. (2012) Gravitational Field of Gyratons Propagating on Backgrounds Formed by Direct-Product Spacetimes. In: Damour, T. and Jantzen, R., Eds., The 12th Marcel Grossman Meetings of General Relativity Proceedings, Vol. 3, World Press Scientific, Singapore, 1899-1901.
- 37. Kadlecova, H., Zelinikov, A., Krtous P. and Podolsky, J. (2009) Gyratons on Direct-Product Spacetimes. Physical Review D, 80, Article ID: 024004. https://doi.org/10.1103/PhysRevD.80.024004
- 38. Abbott, B.P., et al. (2016) Observation of Gravitational Waves from a Binary Black Hole Merger. Physical Review Letters, 116, Article ID: 061102. https://physics.aps.org/featured-article-pdf/10.1103/PhysRevLett.116.061102 https://doi.org/10.1103/PhysRevLett.116.061102
- 39. Corda, C. (2009) Interferometric Detection of Gravitational Waves: The Definitive Test for General Relativity. International Journal of Modern Physics D, 18, 2275-2282. https://doi.org/10.1142/S0218271809015904
- 40. Abbot, B.P., et al. (2016) GW151226: Observation of Gravitational Waves from a 22-Solar-Mass Binary Black Hole Coalescence. Physical Review Letters, 116, Article ID: 241103. https://doi.org/10.1142/S0218271809015904
- 41. Halliwell, J. (1990) Quantum Cosmology. In: Pati, J.C., Randjbar-Daemi, S., Sezgin, E. and Shafi, Q., Eds., The ICTP Series in Theoretical Physics, Vol. 7, Word Scientific, Singapore, 515-599.
- 42. Penrose, R. (2011) Cycles of Time. Alfred Knopf, New York.
- 43. Thompeson, M. (2008) Modern Particle Physics. Cambridge University Press, Cambridge, UK.
- 44. Arraut, I. The Higgs Mechanism at the Graviton Level: The Vainshtein Mechanism in Time-Domains. https://arxiv.org/abs/1505.06215v3
- 45. Oda, I. (2010) Remarks on Higgs Mechanism for Gravitons. Physics Letters B, 690, 322-327. https://arxiv.org/abs/1004.3078 https://doi.org/10.1016/j.physletb.2010.05.048
- 46. Canate, P., Jaime, L. and Salgado, M. (2016) Spherically Symmetric Black Holes in f(R) Gravity: Is Geometric Scalar Hair Supported? Classical and Quantum Gravity, 33, 42 p.
- 47. Beckwith, A. (2016) Open Question: Could a Causal Discontinuity Explain Fluctuations in the CMBR Radiation Spectrum? Journal of High Energy Physics, Gravitation and Cosmology, 2, 186-208. https://doi.org/10.1016/j.physletb.2010.05.048
- 48. Clarkson, C. and Seahra, S. (2007) A Gravitational Wave Window on Extra Dimensions. Classical and Quantum Gravity, 24, F33. https://doi.org/10.1088/0264-9381/24/9/F01
- 49. Mueller, R. and Lousto, C. (1995) Entanglement Entropy in Curved Spacetime with Event Horizons. Physical Review Journals, 52, 4512-4517. https://arxiv.org/abs/gr-qc/9504049
- 50. Sticlet, D. Phase Transitions in the Early Universe, Electroweak and QCD Phase Transitions. http://fyzika.uniza.sk/~melo/DoruSticlet.pdf
- 51. Shankar, R. (2016) Fundamentals of Physics, II, Electromagnetics, Optics and Quantum Mechanics. Yale University Press, New Haven, CT.
- 52. Penrose, R. (1966) General-Relativistic Energy Flux and Elementary Optics. In: Hoffman, B., Ed., Perspectives in Geometry and Relativity, Indiana University Press, Indiana, USA, 259.
- 53. Hooft, G. (2002) Determinism beneath Quantum Mechanics. Conference Proceedings, “Quo Vadis Quantum Mechanics”, Philadelphia, 12 pages, 1 Figure Postscript. https://arxiv.org/abs/quant-ph/0212095
- 54. Gron, O. and Hervik, S. (2002) The Weyl Curvature Conjecture. arXiv:gr-qc/0205026.
- 55. Belinskii, V.A., Khalintnikov, I.M. and Lifschitz, K. (1971) Oscillatory Approach to the Singular Point in Relativistic Cosmology. Sov. Phys. Usp., 13, 745-765. [Belinskii, V.A., Khalintnikov, I.M. and Lifschitz, K. (1971) Oscillatory Approach to the Singular Point in Relativistic Cosmology. Advances in Physics, 19, 525.]
- 56. Ortaggio, M. and Pravdová, A. (2014) Asymptotic Behavior of the Weyl Tensor in Higher Dimensions. Physical Review D, 90, Article ID: 104011. https://arxiv.org/abs/1403.7559 https://doi.org/10.1088/0264-9381/24/9/F01
- 57. Hawking, S.W. and Ellis, G.F.R. (1973) The Large Scale Structure of Space-Time. Cambridge Monographs on Mathematical Physics, Cambridge University Press, Cambridge, UK. https://doi.org/10.1017/CBO9780511524646
- 58. Wesson, P.S. (2006) Five Dimensional Physics, Classical and Quantum Consequences of Kaluza-Klein Theory. World Press Scientific, Singapore.
- 59. Kramer, D., Stephani, H. and Herlt, E.M. (1979) MacCallum. In: Schmutzer, E., Ed., Exact Solutions of Einstein Field Equations, Cambridge University Press, Cambridge, UK, VEB Deutscher Verlag der Wissenschaften, Berlin, Germany, 109.
- 60. Misner, C.W., Thorne, K.S. and Wheeler, J.A. (1973) Gravitation. Princeton University Press, Princeton, New Jersey, USA.
- 61. Sciama, D. (1953) On the Origins of Inertia. Monthly Notices of the Royal Astronomical Society, 113, 34. http://adsabs.harvard.edu/abs/1953MNRAS.113...34S
- 62. Paul, T.K. (1993) Mach’s Principle and Isotropic Singularities. In: Ellis, G., Lanza, A. and Miller, J., Eds., The Renaissance of General Relativity and Cosmology: A Survey to Celebrate the 65 Birthday of Dennis Sciama, Cambridge University Press, Cambridge, UK, 234-247.
- 63. Lightman, A.P., Press, W.H., Price, R.H. and Teukolsky, S.A. (1975) Problem 12.16. In: Lightman, A.P., Ed., Problem Book in Relativity and Gravitation, Princeton University Press, Princeton, NJ, 74.
- 64. Deser, S., Jackiw, R. and Templeton, S. (1982) Topologically Massive Gauge Theories. Annals of Physics, 140, 372-411. https://doi.org/10.1016/0003-4916(82)90164-6
- 65. Maggiore, M. (2008) Gravitational Waves: Volume 1: Theory and Experiment. Oxford University Press, Oxford, UK.
- 66. Raine, D. (1993) Decoherence of the Cluttered Quantum Vacuum. In: Ellis, G., Lanza, A. and Miller, J., Eds., The Renaissance of General Relativity and Cosmology: A Survey to Celebrate the 65 Birthday of Dennis Sciama, Cambridge University Press, Cambridge, UK, 300-313. https://doi.org/10.1017/CBO9780511622724.020
- 67. Unruh, W.G. (1986) Why Study Quantum Theory? Canadian Journal of Physics, 64, 128-130. https://doi.org/10.1139/p86-019
- 68. Unruh, W.G. (1986) Erratum: Why Study Quantum Theory? Canadian Journal of Physics, 64, 1453. https://doi.org/10.1139/p86-257 http://www.nrcresearchpress.com/doi/10.1139/p86-257#.WsQwei5uaM-
- 69. Kolb, E. and Turner, S. (1991) The Early Universe. Westview Press, Chicago, USA.
- 70. Benaoum, H.P. (2012) Modified Chaplygin Gas Cosmology. Advances in High Energy Physics, 2012, Article ID: 357802. http://arxiv.org/abs/1211.3518 https://doi.org/10.1155/2012/357802
- 71. Schief, W.K. and Rogers, C. (1999) Binormal Motion of Curves of Constant Curvature and Torsion. Generation of Soliton Surfaces. Proceedings: Mathematical, Physical and Engineering Sciences, 455, 3163-3188. http://www.jstor.org/stable/53475?seq=1#page_scan_tab_content
- 72. Biermann, P. and Harms, B. Time Jitter Due to Gravitational Solitons. http://www.phy.olemiss.edu/GR/GCGM7Talks/Harms.pdf
- 73. Hanson, A.J. and Eguchi, T. Gravitational Instantons. https://www.cs.indiana.edu/~hansona/papers/EguchiHanson-GenRelGrav1979.pdf
Appendix A
Brief introduction as to Quantum infinite statistics as offered by Ng. in [31]
As described in [31] the idea is as follows
As used by Ng [31]
(A1)
This, according to Ng [4] , leads to entropy of the limiting value of, if will be modified by having the following done, namely after his use of quantum infinite statistics
(A2)
Appendix B
Randall Sundrum effective potential
The consequences of the fifth-dimension show up in a simple warped compactification involving two branes, i.e., a Planck world brane, and an IR brane. Let’s call the brane where gravity is localized the Planck brane This construction permits (assuming K is a constant picked to fit brane world requirements) [18] [19]
(B1)
Here, what is called can be linked to Kaluza Klein “excitations” via (for a number n > 0)
(B2)
To build the Kaluza-Klein theory, one picks an invariant metric on the circle S1 that is the fiber of the U(1)-bundle of electromagnetism. This leads to construction of a two component scalar term with contributions of different signs. i.e. [18]
(B3)
We should briefly note what an effective potential is in this situation. [18]
We get
(B5)
This above system has a metastable vacuum for a given special value of . Start with [18] [27]
(B6)
As given in [19]
(B7)
Part of the integrand in Equation (B4) is known as an action integral, , where L is the Lagrangian of the system. Where as we also are assuming a change to what is known as Euclidean time, via , which has the effect of inverting the potential to emphasize the quantum bounce hypothesis of Sidney Coleman. In that hypothesis, L is the Lagrangian with a vanishing kinetic energy contribution, i.e. , where V is a potential whose graph is “inverted” by the Euclidian time. Here, the spatial dimension is defined so that [19]
(B8)
and
(B9)
We should note that the quantity referred to above has a shift in minimum energy values between a false vacuum minimum energy value, Efalse min, and a true vacuum minimum energy Etrue min, with the difference in energy reflected in Equation (B9) above.
This requires, if we take this analogy seriously the following identification with what was done by the Japanese theorists
(B10)
So that one can make equivalence between the following statements. These need to be verified via serious analysis.
(B11)
(B12)
Appendix C
Summary of material from [51] [31] as to quantum mechanical probability for particle to stay in ground state. For a box, with a wave functional as described below.
Assume a normalized quantum mechanical wave functional, ψ as given by [51]
(C1)
If so then, the probability that one has a wave functional value with n = 1 in the situation defined by Equation (C1) (A1) is given as
(C2)
Appendix D
Making sense of the Penrose reference, as to nonzero initial entropy, and other cosmological issues.
In [24] Penrose, makes the following claim, and we will be examining its implications. He claims that
“An oscillatory Weyl curvature of frequency and complex amplitude Y supplies an effective “gravitational-energy” contribution to the Ricci tensor [32] of magnitude
(D1)
Before approach to a singularity
The assumption, is that at the singularity, that the complex amplitude, Y is set equal to zero. And so there is no gravitational energy, at a singularity.
Our suggestion is that Equation (D1) never goes to zero, due to Equations ((3) to (5)) of our text, and that due to this, we will be having, instead, that the nonzero value of Equation (D1) is a condition for initial graviton production. Hence, then, using [31] and infinite quantum statistics, we are having, then that graviton production, then will be linked to entropy production, at the start of a causal boundary, of space-time.
This should be compared with [54] and with [55] which according to Penrose gives a far more detailed proof, and also we can connect it with [56] in terms of an eventual calculation which will be linked to some of the Pre-Planckian space- time results of [23] and also [47] .
The long and short of it is also that if we understand what the consequences of a causal discontinuity are, we will be able to perform a detailed calculation of the Weyl curvature tensor in the neighborhood of a near singular starting point of space-time. Doing that is equivalent to the following
a) Detailing a relic initial graviton rate, for the start of expansion from a causal discontinuous bubble of space-time
b) Detailing a physical mechanism for the production of nonzero entropy at the start of cosmological expansion
c) Re do of Equations ((4), (5) and (18)) of our document, due to a re interpretation of [24] , with a nod to [54] [55] [56] of our document
d) Detailed calculations of the Weyl tensor in the neighborhood of the Causal boundary.
e) A review of the physics, of presumed singularity theorems as given in [57] plus [37] [58] .
Appendix E
The Weyl curvature tensor, in the Friedman-Lemaitre-Robertson-Walker (FLRW) metric and what it says about Pre Planckian-Planckian transformations
We initiate this section by stating the n = 4 (three spatial dimensions and one time dimension) Weyl Tensor, in the case of a fluid cosmology, a.k.a. the Friedman- Lemaitre-Roberson-Walker metric
We write for the Weyl curvature Tensor, a formulation given by [38] [59] , which we rewrite as
(E1)
The entries into the above, assuming c = 1 (speed of light) in the Friedman- Lemaitre-Roberson-Metric would be right after the Causal boundary, in the Neighborhood of Planckian Physics, given as [60] , namely looking at the so called entries into the following expressions, namely if we go by [6]
(E2)
In the Pre Planckian space-time, we will have that about the Causal boundary, were H = 0 we will have
(E3)
It so happens, that for very small time steps, with the inflaton, as given by Equation (5) in the main text would be negative, i.e.
(E4)
Our task would be to fill in the details of the evolution of the metric tensor, as far as Pre Plankian space-time and to find a way analytically to obtain an expression, which would in some sense have an analytical linkage, prior to the space- time given in (E1) above.
This will be the task of our future analytical work, and its possible connection to the Penrose Weyl Hypothesis, and singularities, as given in [24]
Appendix F
Mach’s principle as written by Sciama, in defining the initial space-time non-singular ‘bubble.
For the sake of completeness we reproduce Equations ((19) to (21)) of the text, but with the commensurate references, and include in their references, with suitable explanations included.
Our starting equation is given by Sciama, as given in [61] , which is rendered as
(F1)
Reference [62] gives further insights, into how Sciama worked with this insight, but for the Pre-Planckian to Planckian space-time physics, we will stick for the moment with looking at the intricacies of the Equation (F1)
In defining the initial space-time non-singular ‘bubble. If, here, τ is a time unit, which is interpreted slightly differently than being the Hubble time, but instead is the recounting is given as
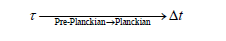 (F2)
(F2)
Whereas we will be interpreting
 (F3)
(F3)
The discussion of the applications of Equations ((F2) and (F3)) are linked with suitable references, and also are tied, into an interpretation of Equation (D4) in a way which introduces the idea of quantum mechanics being introduced, near the causal boundary surface as referenced in Equation (14) in a way which makes our interpretation of space-time gravitational wave signals being produced, also, in effect, linked to when holds, in effect transforming it to a data set we will call
 (F4)
(F4)
This is our final future works project which we will attempt to confirm or to analyze via future data sets, and we will do it while asserting that Dt is tied into a solution to Equation (12) of the main text.
Here we refer to these equations as having to be checked against the predictions given in gravitational wave physics problems [63]
We also state for the record that this is assuming massive gravitons. i.e. we work with the following given value
(F5)
This is, then of course in sync with [64] as well, and should be made consistent with respect to future gravitational wave astronomy data sets. A future works project which we think is essential, where one has to keep in mind that the Compton wavelength of the graviton is not equal to the gravitational wave wavelength. Instead, the lower-bound graviton Compton wavelength is 5 × 109 times greater than the gravitational wavelength for the GW150914 event, which was ~ 2000 km.
Clarifying this last point with sufficient data analysis, will entail a close check with [38] [39] [40] . And of course interested readers are invited to look at the theoretical massive gravity theoretical details which are in [65] . Also, in [66] there is a very detailed discussion of a quantum oscillator, assuming a mass, m, distance d, and temperature T, which is a length of the traversing of our formed quantum mechanical states, possibly of gravitons, to emerge as a classically inclined decoherence state, in a time, t, as given by the [66] result, as
(F6)
Of course, reconciling Equation (F5) (D5) and the discussion between Equations ((F5) and (F6)) should be part of our future works program, as well as all the other issues alluded to by Dr. Corda in [39] which is very relevant. In doing so, this should give more detail as to Equation (4) In the main text.
One possible end run about the difference in Graviton Compton wavelength, and of Gravitational wave wavelength, this of the fact that lower-bound graviton Compton wavelength is 5 × 109 times greater than the gravitational wavelength
Look at the special relativistic proportionality factor of increase in mass is included in, we would be obtaining the very high relativistic
(F7)
i.e. this would be in line with the situation where one has a mass of the graviton, at near light speed being greater than the presumed rest mass of the “massive” graviton, which would be a staggering increase in the effective mass of gravitons, traveling near the speed of light, right after the H = 0 causal boundary surface.
In itself this would be lending toward trying to ascertain experimental data set confirmation if this is viable and a reasonable datum to consider in this situation. As a datum which may explain the black hole situation as outlined above.
Appendix G
Summary of the changes of the Pre Planckian to Planckian Heisenberg Uncertainty principle to keep in mind.
We use the approximation as presented in [25] which we reproduce below as also in [67] [68]
(G1)
If we use the following, from the Roberson-Walker metric [67] [68] [69]
(G2)
Following Unruh [67] [68] , write then, an uncertainty of metric tensor as, with the following inputs
(G3)
Then, if [25] [67] [68]
(G4)
This Equation (G4) is such that we can extract, up to a point the HUP principle for uncertainty in time and energy, with one very large caveat added, namely if we use the fluid approximation of space-time [69]
(G5)
Then by [25]
(G6)
Then, by [25]
(G7)
This leads to us estimating of the term in Modified HUP, as a summary of what we obtain here, is if we use something similar to the Chapygin gas model [70]
(G8)
For our purposes, this corresponds to having fairly large but not infinite,
(G9)
Appendix H
Brief commentary as to how to have the onset of Gravitational waves, at the boundary of a Causal bubble of space-time
Intuitively, this appears to be impossible. It would be if there was no turbulence, or variation in initial space-time structure. To give an argument which purports to show otherwise, we will reference the following
In [71] the authors of that manuscript make direct reference to the creation of a soliton surface, and do it with respect to a Backlund transformation
Quote:
The purely binormal motion of curves of constant curvature or torsion, respectively, is shown to lead to integrable extensions of the Dym and classical sine-Gordon equations. In the case of the extended Dym equation, a reciprocal invariance is used to establish the existence of novel dual-soliton surfaces associated with a given soliton surface. A cc?ideal formulation is adduced to obtain a matrix Darboux invariance for the extended Dym and reciprocally linked m2KdV equations. A Bäcklund transformation with a classical constant-length property is thereby constructed which allows the generation of associated soliton surfaces. Analogues of both Bäcklund’s and Bianchi’s classical transformations are derived for the extended sine?Gordon system.
End of quote
What we will investigate in a later publication is if the interplay between a single inflaton field, with its subsequent evolution to a multiple valued inflaton field, right at the onset of Planckian Space-time, at the causal boundary will in itself be necessary and sufficient for the generation of an inflaton generated (multiple branch) associated soliton surface.
It appears then to be a very hard slog from there to gravitons. Fortunately though,. [72] give a way to link what we are talking about to Gravitons, See page six of their presentation, where they work with
Quote:
Stimulated emission of gravitons due to interaction of soliton on weak gravity- brane with strong-gravity brane
End of quote
We argue that our causal boundary surface, as an interaction zone between a single inflaton field, branching off to a multiple inflaton filed, will create a situation similar to their Figure 2, of their presentation.
The details of this will be filled out in a future publication. But we also refer the reader to [73] which shows one of the earlier attempts at gravitational instantons which is readily accessible and also gets the main idea across.

