Journal of High Energy Physics, Gravitation and Cosmology
Vol.03 No.01(2017), Article ID:72152,7 pages
10.4236/jhepgc.2017.31002
Initial Mass in Pre-Planckian Space-Timed Defined, and Causal Discontinuity
Andrew Walcott Beckwith
Physics Department, College of Physics, Chongqing University Huxi Campus, Chongqing, China

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: August 5, 2016; Accepted: November 15, 2016; Published: November 21, 2016
ABSTRACT
This document reviews the Landau-Liftshifts reformulation of General relativity with a representation of the available mass of a graviton. From looking at a conservation law, using the Landau-Liftshifs formulation, we obtain conditions for initial mass, in the Pre-Planckian regime of space-time. In doing so, we also indicate a metric tensor and metric pseudo tensor delineation of causal discontinuity.
Keywords:
Massive Gravitons, Landau-Liftshifts Pseudo Tensor, Causal Discontinuity

1. Introduction
We will use the Poisson formulation of the Landau-Liftshifts formulation of General Relativity [1] in order to obtain an initial mass, in the Pre-Planckian Regime of space time. Using a modification of the Heisenberg Uncertainty principle, we also obtain an inter relationship between an inflation, initially, and initial mass. Finally, we reference the issue of a causal discontinuity, with surprising implications.
We first begin by a recapitulation of the different models for HFGW as given by Dr. Li et al., 2008 [2] .
This reproduced PRD table [3] is important since it suggests that relic GW, if properly measured, may be the first ones to await experimental verification. But in order to do this, we add in several caveats, as to after the fact considerations.
We are considering using massive gravitons [4]
1. Our methodology suggests that if we measure relic gravitational waves, that we will have to consider if an initial mass in the evolution of the universe, actually existed [1] .
We also review, by example, if there is a way to use a modified version of the Heisenberg uncertainty principle, as given in [5] .
2. To obtain an inflation, in the onset of expansion of the Universe.
By way of our construction, we will also look at if a causal discontinuity exists as an elaboration of [3] .
Having said that, it is time now to unveil by way of the Poisson reference [1] initial mass, and to tie it into our four issues brought up above. But before this, we will allude to our basic work horse, i.e. the Ng Entropy.
We wish to understand the linkage between dark matter and gravitons. To consider just that, we look at the “size” of the nucleation space, V. V for nucleation is HUGE. Graviton space V for nucleation is tiny, well inside inflation/therefore, the log factor drops OUT of entropy S if V chosen properly for both Equation (1) and Equation (2). Ng’s [6] result begins with a modification of the entropy/partition function Ng used the following approximation of temperature and its variation with respect to a spatial parameter, starting with temperature 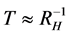 (
(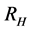 can be thought of as a representation of the region of space where we take statistics of the particles in question). Furthermore, assume that the volume of space to be analyzed is of the form
can be thought of as a representation of the region of space where we take statistics of the particles in question). Furthermore, assume that the volume of space to be analyzed is of the form 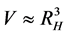 and look at a preliminary numerical factor we shall call
and look at a preliminary numerical factor we shall call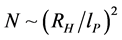 , where the denominator is Planck’s length (on the order of 10−35 centimeters). We also specify a “wavelength” parameter
, where the denominator is Planck’s length (on the order of 10−35 centimeters). We also specify a “wavelength” parameter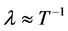 . So the value of
. So the value of  and of
and of 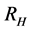 are approximately the same order of magnitude. Now this is how Jack Ng changes conventional statistics: he outlines how to get
are approximately the same order of magnitude. Now this is how Jack Ng changes conventional statistics: he outlines how to get , which with additional arguments we refine to be
, which with additional arguments we refine to be  (where
(where  is graviton density). Begin with a partition function
is graviton density). Begin with a partition function
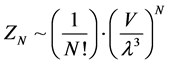 (1)
(1)
This, according to Ng, [6] leads to entropy of the limiting value of, if 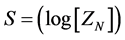
 (2)
(2)
But . The modification of Ng’s entropy expression [6] is in the region of space time for which the general temperature dependent entropy Kolb and Turner expression breaks down. In particular, the evaluation of entropy we do via the modified Ng argument above is in regions of space time where
. The modification of Ng’s entropy expression [6] is in the region of space time for which the general temperature dependent entropy Kolb and Turner expression breaks down. In particular, the evaluation of entropy we do via the modified Ng argument above is in regions of space time where  before re heat is an unknown, unmeasurable number of degrees of freedom The Kolb and Turner entropy expression [7] 1991 has a temperature
before re heat is an unknown, unmeasurable number of degrees of freedom The Kolb and Turner entropy expression [7] 1991 has a temperature  related entropy density which leads to that we are able to state total entropy as the entropy density time’s space time volume
related entropy density which leads to that we are able to state total entropy as the entropy density time’s space time volume  with
with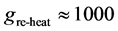 , while dropping to
, while dropping to 



where
Such a linkage would open up the possibility that the density of primordial gravitational waves could be examined, and linked to modeling gravity as an effective theory. The details of linking what is done with Equation (2) and bridging it to Equation (3) await additional theoretical development, and are probably conceptually understandable if the following is used to link the two regimes. i.e. we can use the number of space time operations used to create Equation (2), via Seth Lloyds [8]

Essentially, what will be done is to use Equation (4) to show linkage between a largely thermally based production of entropy, as implied by Equation (3) and a particle counting algorithm, as given by Equation (2). This due to the problems inherent in making connections between a particle count generation of entropy, and thermal contributions. i.e. two different processes are involved.
2. The Poisson Rendition of the Landau-Liftshitz Effective Initial Mass
To do this go to [1] and the non Tensorial form of the Einstein field equations starting with the so called Gothic inverse metric, with a 2n line of Equation (5) being a tensor identity

Furthermore, the two equations in Equation (5) have a representation of the GR field equations as

If so then, we can have a simple solution to this above which is of the type

Here, in this situation we have that if we are following the ideas in [5] .
where we have restriction to the zeroth (time component) of the metric tensor, so that

We will be looking at the value of Equation (7) if

If we use the following, from the Roberson-Walker metric [9] [10] [11] .

Then, the surviving version of Equation (9) and Equation (10) is, then, if 

This Equation (11) is such that we can extract, up to a point the HUP principle for uncertainty in time and energy, with one very large caveat added, namely if we use the fluid approximation of space-time [5]

Then by [10] [11]

Then,

Here, we have a causal discontinuity as given by

We will address the implications of Equation (15) in the conclusion
If we then put in the initial mass, of say from [1] of

With the minimum scale factor a small, but non zero factor by [12] which is shown up in

3. Conclusion, Implication of Causal Discontinuity as Implied by Equation (17)
Note that having the right hand side of the 2nd line of Equation (17) going to zero is implying that there is an invariance as to the gravitational field pseudo tensor, which may have implications as to the entropy-information transfer from Pre-Planckian to Planckian space-time, however we have to consider the Pre-Planckian to Planckian physics of the more traditional stress energy tensor.
What we will say, is that by [5] and [13] if we have that the 2nd line of Equation (17) equals zero, with this reflecting the 


Dispersal of the terms alpha and beta, into the non time components of the stress energy tensor would be saying also that

Note that in [13] we have that
Quote
These gapless Goldstone modes are the quantum carriers of information and entropy. Analyzing their effective theory, we observe the information-processing properties strikingly similar to the ones predicted by the black hole portrait. The energy cost per qubit of information-storage vanishes in the large-N limit and the total information-storage capacity increases with N either exponentially or as a power law.
End of quote
Our idea is that the N limit, of information entropy, is akin to graviton counting, using the information given in Section 2, as given by Ng [6] and that if or not we have gravitons in a counting mode will be strongly affected by a possible causal discontinuity as given by Equation (19). If or not we have a causal continuity or discontinuity will also be affected by the simple minded rendition of inflation physics, whereas

If N being a graviton count is sufficiently large, and the initial inflation can be parameterized, we can understand if or not Equation (19) is a causal structure discontinuity.
Furthermore, understanding Equation (17) to Equation (20) more fully may allow us to choose between the different models given in Table 1, among other things looking at if the following is true, namely.
Note that usual Randal Sundrum brane theory has a production rate [14] [15] of

As the number of Kaluza Klein gravitons per unit time per unit volume Note that this production rate is for a formula assuming mass for which


Table 1. Magnitude, sources, and top frequency values for HFGW (from Li et al. 2008) [3] .
where R is the assumed higher dimension “size” and, d is the number of dimensions above 4, and typically we obtain
This with additional work may allow us to distinguish between the GW and gravity models as given in reference [16] by Corda as well as giving more definition to the issues brought up the the LIGO analysis of gravitational waves, as given in [17] and [18] .
Acknowledgements
This work is supported in part by National Nature Science Foundation of China grant No. 11375279.
Cite this paper
Beckwith, A.W. (2017) Initial Mass in Pre-Planckian Space- Timed Defined, and Causal Discontinuity. Journal of High Energy Physics, Gravitation and Cosmology, 3, 9-15. http://dx.doi.org/10.4236/jhepgc.2017.31002
References
- 1. Poisson, E. and Will, C. (2014) Gravity, Newtonian, Post Newtonian, and Relativistic. Cambridge University Press, Cambridge, UK.
https:/doi.org/10.1017/CBO9781139507486 - 2. Li, F., Yang, N., et al. (2008) Using Polarized Maser to Detect High-Frequency Relic Gravitational Waves. Physical Review D, 78, 024041.
http://arxiv.org/abs/0807.0885
https:/doi.org/10.1103/PhysRevD.78.024041 - 3. Zakharov, V.I. (1970) Linearized Gravitation Theory and the Graviton Mass. JETP Letters, 12, 312.
Bibcode:1970JETPL..12..312Z - 4. Beckwith, A. (2016) Gedanken Experiment for Refining the Unruh Metric Tensor Uncertainty Principle via Schwarzschild Geometry and Planckian Space-Time with Initial Nonzero Entropy and Applying the Riemannian-Penrose Inequality and Initial Kinetic Energy for a Lower Bound to Graviton Mass (Massive Gravity). Journal of High Energy Physics, Gravitation and Cosmology, 2, 106-124.
https:/doi.org/10.4236/jhepgc.2016.21012 - 5. Beckwith, A. (2016) Open Question: Could a Causal Discontinuity Explain Fluctuations in the CMBR Radiation Spectrum? Journal of High Energy Physics, Gravitation and Cosmology, 2, 186-208.
https:/doi.org/10.4236/jhepgc.2016.22018 - 6. Ng, Y. (2008) Spacetime Foam: From Entropy and Holography to Infinite Statistics and Nonlocality. Entropy, 10, 441-461.
https:/doi.org/10.3390/e10040441 - 7. Kolb, E. and Turner, S. (1994) The Early Universe. Westview Press, Chicago.
- 8. Lloyd, S. (2002) Computational Capacity of the Universe. Physical Review Letters, 88, Article ID: 237901.
https:/doi.org/10.1103/PhysRevLett.88.237901 - 9. Gorbunov, D. and Rubakov, V. (2011) Introduction to the Theory of the Early Universe, Cosmological Perturbations and Inflationary Theory. World Scientific Publishing Pte. Ltd., Singapore.
- 10. Unruh, W.G. (1986) Why Study Quantum Theory? Canadian Journal of Physics, 64, 128-130.
https:/doi.org/10.1139/p86-019 - 11. Unruh, W.G. (1986) Erratum: Why Study Quantum Gravity? Canadian Journal of Physics, 64, 128-130.
https:/doi.org/10.1139/p86-019 - 12. Beckwith, A. (2016) Gedanken Experiment for Delineating the Regime for the Start of Quantum Effects, and Their End, Using Turok’s Perfect Bounce Criteria and Radii of a Bounce Maintaining Quantum Effects, as Delineated by Haggard and Rovelli. Journal of High Energy Physics, Gravitation and Cosmology, 2, 287-292.
https:/doi.org/10.4236/jhepgc.2016.23024 - 13. Dvali, G., Franca, A., Gomez, C. and Wintergerst, N. (2015) Nambu-Goldstone Effective Theory of Information at Quantum Criticality. Physical Review D, 92, Article ID: 125002.
arXiv:1507.02948v1 [hep-th]
https:/doi.org/10.1103/physrevd.92.125002 - 14. Rubakov, V.A. (2001) Large and Infinite Extra Dimensions. Physics-Uspekhi, 44, 871-893.
http://arxiv.org/pdf/hep-ph/0104152.pdf https:/doi.org/10.1070/PU2001v044n09ABEH001000 - 15. Rubakov, V. (2002) Classical Theory of Gauge Fields. Translated by Wilson, S.S., Princeton University Press, Princeton, 456 p.
- 16. Corda, C. (2009) Interferometric Detection of Gravitational Waves: The Definitive Test for General Relativity. International Journal of Modern Physics D, 18, 2275-2282.
arXiv:0905.2502 [gr-qc]
https:/doi.org/10.1142/S0218271809015904 - 17. Abbott, B., et al. (2016) Observation of Gravitational Waves from a Binary Black Hole Merger. LIGO Scientific Collaboration and Virgo Collaboration. Physical Review Letters, 116, Article ID: 061102.
https://physics.aps.org/featured-article-pdf/10.1103/PhysRevLett.116.061102
https:/doi.org/10.1103/physrevlett.116.061102 - 18. Abbott, B., et al. (2016) GW151226: Observation of Gravitational Waves from a 22-Solar-Mass Binary Black Hole Coalescence. LIGO Scientific Collaboration and Virgo Collaboration. Physical Review Letters, 116, Article ID: 241103.
https:/doi.org/10.1103/physrevlett.116.241103


