Received 29 October 2015; accepted 26 December 2015; published 29 December 2015

ABSTRACT

We will be looking at the energy of a graviton, based upon the Stress energy tensor, and from there ascertaining how fluctuations in early universe conditions impact the mass of a graviton. Physically the mass of the graviton would be shrinking right after Planck time and presumably it would be going to its equilibrium value of about 10⁻⁶² grams, for its present day value. It, graviton mass, would increase up to the Plank time of about 10⁻⁴⁴ seconds. Note that the result that graviton mass shrinks to 10⁻⁶² grams for its present day value works only for relic gravitons.

Keywords:

Heavy Gravity, Plank Time, Stress Energy Tensor

1. Introduction, Setting up for Calculation of Using the Results of Initial Energy as Due to 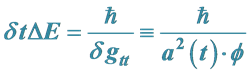and Comparing It to a More General Energy Expression Given Below

Start off with looking at from [1] , a generalized energy expression with momentum also obeying, if m is for graviton mass. Begin with from [1] .

(1)

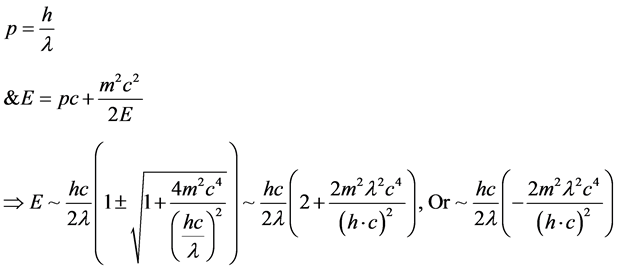(2)

Next, from Giovannini [2] , if T is the trace of the Stress-Energy tensor, we have that

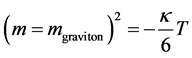(3)

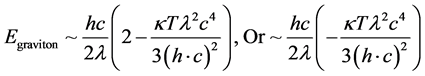(4)

If so, then, the fluctuation of energy would be represented, if 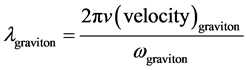and we have [3]

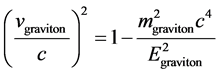(5)

Then if we go to look at what [1] 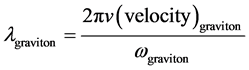then is saying, the above is then rendered

as

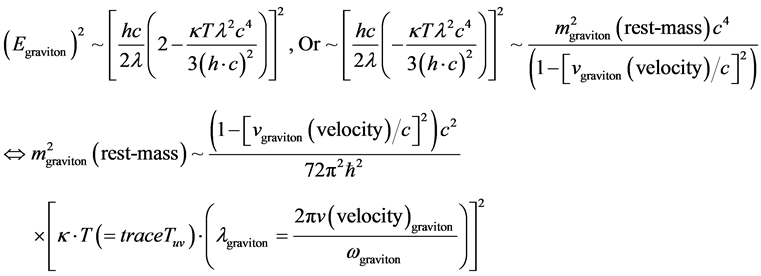(6)

Note that the presence of the mass reduces the speed of gravitons with respect to the speed of light. As has stressed repeatedly by Dr. Corda and his collaborators. Corda and collaborators have stated that this massive graviton mass leads to a situation for which the graviton generates a longitudinal component of strain in the arms of a interferometric detector. This point is made abundantly clear in clarified in the papers of Prof. Corda and collaborators, i.e. see references [4] - [9] . This will be of crucial importance in the concluding remarks of this document. Next. Let us consider what happens if there is a fluctuation in Graviton mass.

2. Utilizing Equation (6) in Terms of the Initial Fluctuation of the Graviton Mass

From [1] [10] - [12] , use

(7)

3. Identifying Change in: This Is the Input into Equation (7), Assuming

We follow what to expect from as given in [1] [2] for

(8)

as a way to quantify energy density when we have what is coming from Weinberg [12] on initial energy density and then from there to say something about initial time step and also potential energy as given Padmanbhan [1] . Doing so will isolate out values of the Potential energy, as in [12] which will then be compared to [1] ’s potential energy value, which in turn gets a value of time, which we will set by first considering the following evolution equation. From [12] ,

(9)

Then, look at from [12] as having the value of, if M is related to mass, with a variable parameter, which can be negative, with then a smallest value of, and a frequent value of as in the case of chaotic inflation. Here in general

(10)

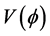
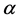
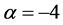
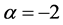
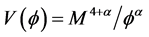
The parameter in the chase of chaotic inflation, i.e. one of the simplest models, whereas it can be positive up to in other models. The results are though that with

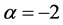
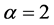
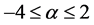
So, then the is given by [12]

(11)

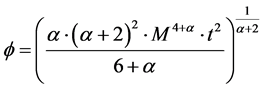
And also look at Padmanabhan’s generalized inflation potential [12] , of comparing Equation (2) with Equation (12) below

(12)

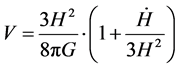
We have the Hubble parameter, if before Planck time, during Plank time

(13)

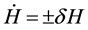
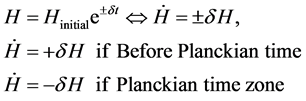
Then, we could get the following variance in time,

(14)

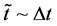
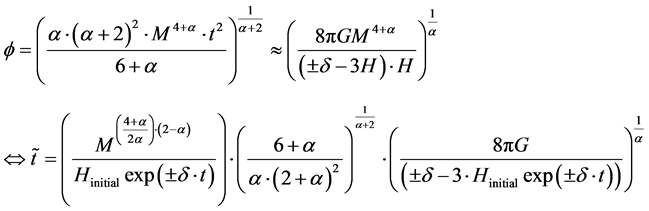
4. Finding How to Use this Value of in Order to Estimate a Relic GW Frequency

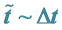
If so, then, up to a point, in the Pre Plankian regime of space time, according to the signs on Equation (13) and

Equation (14) and [10] [11] for the change in Set then, in early universe conditions,

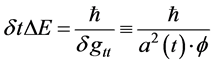
let us set, if we are considering gravitons, that we will set, say that the expression below would be for pre Planckian times, with t < 10⁻⁴⁴ seconds. The upshot would be that there would be a GW frequency, in many cases, as a result of pre Planckian physics of greater than or equal 10³² Hz, which would be red shifted down to about 10¹⁰ Hz, i.e. a 22 order of magnitude drop, in the present era. 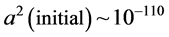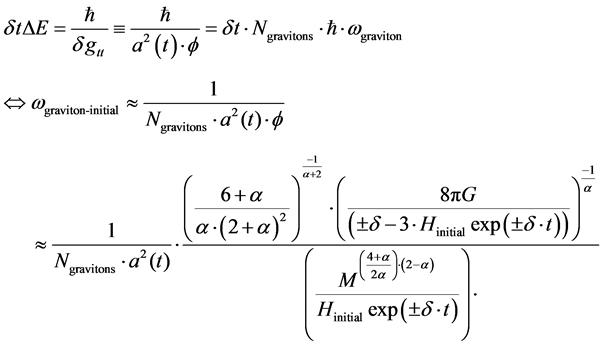This is assuming, as well as we are assuming N ~ 10³⁷, as seen in [10] [11]

(15)

The M as given in this would correspond to the Mass value of the universe, which is roughly 3 × 10⁵⁵ g (where g is for grams) [13] .

5. Conclusion: Putting Equation (15) into Equation (7). What It Says, Physically

Note that time in Equation (14) remains finite but very small, as it came out less than 10 to the minus 44 power seconds, less than Planck time, with the parameter usually less than 2. Time, in Equation (14) as estimate is actually negative, unless we have that we chose in Equation (14) the Pre Planckian option, which is saying that likely Planck time may not be the earliest sub division of time as we know it. This last point above will be important in our future research. As well as entropy production models due to discussions in [14] - [18] in terms of entropy generation in the Pre Planckian era. The entropy values will influence the N used in Equation (15) above. After this is set, for Equation (15) we put Equation (15) into Equation (7) and thereby obtain

(16)

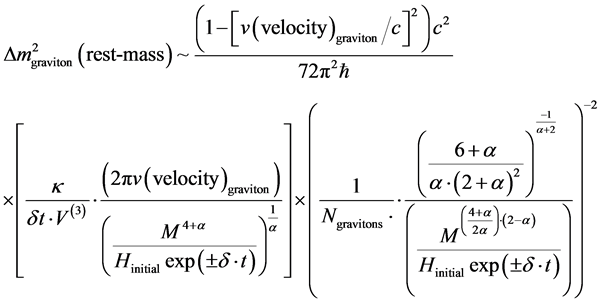
The first term of Equation (16) roughly cancels with the number of gravitons, which approximately leaves

(17)

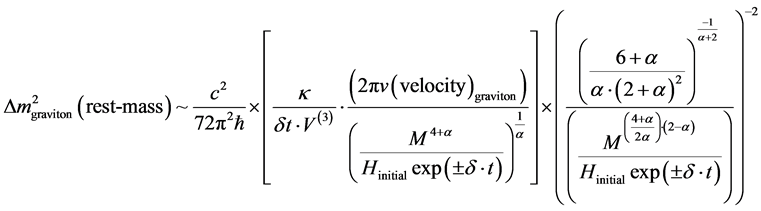
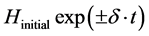
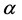
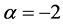
The change in graviton mass is not so much affected by N, entropy count, as this is partly neutralized by the near speed of light conditions, for massive gravitons. What is left though is the variation in total mass, M is divided by, which expands during the Pre Planckian space-time regime, and which shrinks right after Planckian time is breached, in the Planckian era (the Universe begins a massive deceleration. The term would usually be expected to be less than 2. With, and chosen in the case of the very simple chaotic inflationary model.

Physically what this is saying is that the mass of the graviton would be shrinking right after Planck time and presumably it would be going to its equilibrium value of about 10⁻⁶² grams [19] , for its present day value. It, graviton mass, would increase up to the Plank time of about 10⁻⁴⁴ seconds, i.e. the graviton will shrink to 10⁻⁶² grams in the onset of inflation right after 10⁻⁴⁴ seconds, for a stable value of rest graviton mass up to the present day. We also, again state the critical importance of [4] - [9] as far as the physics, of the following statement that a massive graviton generates a longitudinal component of strain in the arms of an interferometric detector and that the simplest model to investigate as far as relic conditions would be the chaotic inflationary model chosen if.

Acknowledgements

This work is supported in part by National Nature Science Foundation of China grant No. 11375279.

Cite this paper

Andrew WalcottBeckwith, (2016) Gedanken Experiment for Fluctuation of Mass of a Graviton, Based on the Trace of GR Stress Energy Tensor-Pre Planckian Conditions that Lead to Gaining of Graviton Mass, and Planckian Conditions That Lead to Graviton Mass Shrinking to 10^-62 Grams. Journal of High Energy Physics, Gravitation and Cosmology,02,19-24. doi: 10.4236/jhepgc.2016.21002

References