Journal of Geoscience and Environment Protection
Vol.06 No.12(2018), Article ID:88955,22 pages
10.4236/gep.2018.612002
The Spatial Distribution Pattern Analysis of City Infrastructure Cases of Urban Management
Jiwei Hou1,2, Jianhua Liu1,2*, Siyu Li1,2, Shiran Song1,2, Congcong Li1,2, Yueming Duan2, Baoshan Zeng2
1Key Laboratory for Urban Geomatics of National Administration of Surveying, Mapping and Geoinformation, Beijing, China
2School of Geomatics and Urban Spatial Information, Beijing University of Civil Engineering and Architecture, Beijing, China

Copyright © 2018 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: October 29, 2018; Accepted: December 1, 2018; Published: December 4, 2018
ABSTRACT
The effective disposal of daily city infrastructure cases is an important issue for urban management. To more effectively utilize a large amount of historical cases data collected and accumulated in the urban grid management system, and to analyze their spatial distribution pattern information for city managers, this study used the comparative kernel density analysis method in two types of cases (i.e. power facilities and traffic guardrail) in Xicheng District, Beijing for the year 2016 and 2017. This research analyzes them at different scales (300 m, 600 m, 1,200 m), and the experiment results show that the method of comparative kernel density analysis is able to provide an intuitively spatial visualization distribution analysis of city infrastructure related cases. The quantitative information of spatial agglomeration degree is helpful for city managers making decision.
Keywords:
City Management Cases, Spatial Distribution Analysis, Distribution Scale, Hotspot Distribution

1. Introduction
With the rapid development of urbanization, the amount of city infrastructure related cases in urban management has been increasing exponentially. A large number of urban management cases not only affect the environment of the city, but also cause problems for the residents’ daily life. To solve these problems in an effective way is a key issue for city managers. The government has vigorously promoted the construction of intelligent cities in recent years, and the urban grid management system ( Zhao, 2012 ) can be recognized as a successful instance. After years of serving, the urban grid management system has accumulated many historical data of city infrastructure related cases. To take advantage of this digital urban management system, many researchers use spatiotemporal data analysis techniques to dig deep into the temporal and spatial distribution of urban management cases ( Hajduk , 2016
This paper uses the massive city cases’ management data accumulated in Xicheng District of Beijing, through the intensive study and analysis of urban cases ( Wang & Du, 2014 ; Zarabi et al., 2011 ; Fu et al., 2017 ), and transferred the traditional “passive discovery and prevention” mode into “active prevention and prediction in advance” mode, so that to provide an effective exploratory analysis and visualization method, which can be used as decision references for urban managers.
The structure of this paper is as follows: Section 1 introduces the research area and data types of spatial analysis, and then introduces the ideas and methods of spatial analysis. Section 2 introduces the main ideas of making thermodynamic charts and shows the distribution of important cases. The comparative kernel density analysis and regional variance analysis are used to explore the impact of different spatial scales on the cases distribution. In the end, the conclusion of our study and the outlook of our works are summarized in Section 3.
2. Study Area and Experiment Data
2.1. The Study Area
Xicheng District is located in the middle part of Beijing, shown in red color in Figure 1. It covers an area of 50.70 km2, 15 sub district offices and 258 communities in the area. As the core area of the capital, Xicheng District is an important urban area with a political center, a commercial area and a tourist destination. The specific distribution is shown in Figure 1.
2.2. Experiment Data
The data of city component related cases used in this paper comes from the database of Urban Infrastructure Mobile Management System (UIMMS) of Xicheng District. A total of 4579 cases during the period of January 1st of 2016 to December 31st of 2017 were included. The data are classified into two categories: 1) the 5 kinds of city infrastructure data, it contains communal facilities, road traffic, city environment, landscaping, housing land. 2) Cases data of these city infrastructure, it mainly covers all kinds of manhole covers, power facilities, traffic guardrail, street lamp and so on. There are 87 different types of cases related to the 5 kinds of city infrastructures. Each case record contains the attributes of events, spatial coordinates, and other items related information.
Figure 2 shows the statistics of 5 categories urban management case data in
Figure 1. The study area, located at longitude 116.372514E, latitude 39.918346N, and center of the Beijing.
Figure 2. The statistics of 5 categories urban management case data change from 2016 to 2017.
Table 1. Statistics of top ten types of city management cases.
2016 and 2017. Table 1 shows the basic statistical information of the top 10 types of cases, and power facilities and traffic guardrail are the top two most common cases. Therefore, this paper focuses on these two types.
3. Method
Because the kernel density estimation method does not use the prior knowledge of data distribution and does not attach any assumptions to the data distribution, it is a method to study the characteristics of data distribution from the data sample itself ( Gong et al., 2017 ). So that the kernel density analysis algorithm ( Fu, Li, Yang et al., 2015 ; Shen & Guo, 2014 ) is used to analyze the urban management cases data. Through the correlation analysis between the clustering results and the urban management cases, this study identified the spatial distribution pattern of events and measured the agglomeration degree of spatial distribution. This information will be provided to city managers. Figure 3 shows the flow chart of the procedure.
3.1. The Kernel Density Estimation Method
The Kernel density estimation method is developed from the quadrate counting method ( Okabe, Satoh, & Sugihara, 2009 ), but superior because it considers the relationship between points in the study unit. The original purpose of this method was to obtain a smooth estimation of the probability density from the observed data, based on the premise that there is a potential event density at any location in the study area ( Dai et al., 2015 ; Gamez & Ileana, 2012 ). There are many methods to estimate the event density at any point in the region. The most common one is to take the point as the center of the circle and count the number of events within the radius r of the circle, then divide it by the area of the circle. So the density of s event point can be expressed as follows:
(1)
In the formula, the radius r represents the scale, K (∙) represents the kernel
Figure 3. Procedure of cluster of urban management cases.
density function, it is often symmetric density function and can be understood as the weight of point i. represents the Euclidean distance from point i to point s, the radius r determines the smoothness of density surfaces. The common kernel functions are homogeneous kernel, quadratic kernel, triangular kernel, Gaussian kernel, cosine kernel etc. ( Leszek , 2015
The kernel density estimation method can be accomplished by density analysis, a spatial analysis module in the toolbox of ArcGIS platform. The tool has two key inputs, one is the choice of Population field. The Population field represents the counts or quantities throughout the landscape used to create a continuous surface, which is the weight of the geographical elements to be calculated. For urban management cases, different regions, the importance of different cases is not the same, so here choose the weight of each urban management case to calculate the computation scale of kernel density, there are quantitative differences in different scales of urban management cases in space ( Niemi et al., 2015 ).Therefore, the choice of scales is particularly important for the spatial distribu-tion analysis of urban management cases.
3.2. Region Analysis
Region analysis is mainly based on “region” as the object of analysis and operation (Kim et al., 2017), in order to more clearly see the trends and trajectories found in urban management cases at the macro level. The standard deviation of kernel density at different scales of each sub-district office can be clearly seen by regional analysis, so as to judge the occurrence of cases in each sub-district and the change of kernel density in different scales. In each street area, using the following formula (2) to calculate the standard deviation of kernel density.
(2)
Among the formula, N refers to the number of all raster pixels in the region, represents the kernel density at raster pixel i, and represents the average kernel density of urban management cases in the region.
4. Results and Discussions
For the parameter setting of kernel density estimation method in ArcGIS platform, there are three main parameters: Population field, output pixel size and search area. Population field is set for the weight of each urban management case. The output pixel size is set to 20 m, and the search area is set to 300 m, 600 m and 1200 m respectively. Generally, in Xicheng District, 300 m represents the community level, 600 m represents the street level, and 1200 m represents the whole district level (Jing et al., 2017). In order to clearly show the variation trend of urban management cases under different scales, the regional variance statistics of kernel density are carried out separately for the calculated results.
4.1. Kernel Density Analysis
Figure 4 and Figure 5 show the spatial distribution trend change of power facilities cases and power facilities, traffic guardrail cases and traffic guardrail at different scales. The power facilities cases and traffic guardrail cases are the damage situation of power facilities and traffic guardrail that reported by supervisors.
The power facilities cases mainly concentrated in the east, and traffic guardrail cases mainly concentrated in the south. The distribution of these two kinds of cases gradually increases with scale, the number of the concentrated distribution region is decreasing, and the area of the concentrated distribution region is gradually increasing. When the scale of power facilities cases is small, the concentrated areas are distributed in Shichahai Street, Yuetan Street, Jingrongjie Street, West Chang’an Street and Dazhalan Street. With the scale increases, the appearance of concentrated areas decreases, at 1200 m scale, only the Shichahai Street and Dazhalan Street show obvious concentrated areas. By comparing (Figure 4(a), Figure 4(c), Figure 4(e)) and (Figure 4(b), Figure 4(d), Figure 4(f)), we can see that the distribution area of power facilities cases is related to






Figure 4. Kernel density distribution of “Power Facilities” cases at different scales and Kernel density distribution of “Power Facilities” at different scales. (a) “Power Facilities” cases at 300 m scale; (b) “Power Facilities” at 300 m scale; (c) “Power Facilities” cases at 600 m scale; (d) “Power Facilities” at 600 m scale; (e) “Power Facilities” cases at 1200 m scale; (f) “Power Facilities” at 1200 m scale.






Figure 5. Kernel density distribution of “Traffic Guardrail” cases at different scales and Kernel density distribution of “Traffic Guardrail” cases at different scales. (a) “Traffic Guardrail” cases at 300 m scale; (b) “Traffic Guardrail” at 300 m scale; (c) “Traffic Guardrail” cases at 600 m scale; (d) “Traffic Guardrail” at 600 m scale; (e) “Traffic Guardrail” cases at 1200 m scale; (f) “Traffic Guardrail” at 1200 m scale.
the number of power facilities in the area. The more facilities in the area, the higher incidence of cases in the area.
Traffic guardrail cases are similar to power facilities cases. At small scale, the concentrated areas are scattered in Desheng Street, Zhanlanlu Street, Guang’an Street, Dazhalan Street and Tianqiao Street. With the increase of scale, at 1200 m scale, only the Guang’an Street and Dazhalan Street show obvious concentrated areas. However, we can see from (Figure 5(a), Figure 5(c), Figure 5(e)) and (Figure 5(b), Figure 5(d), Figure 5(f)) comparison that the distribution area of traffic guardrail cases is very limited due to the number of traffic guardrail in this area.
Therefore, it can be seen that at small scale, it can be clearly seen that the relatively concentrated distribution of cases within each street, the spatial distribution of local details is more significant; At large scale, it highlights the overall distribution of cases throughout the entire study area.
4.2. Variance Comparison
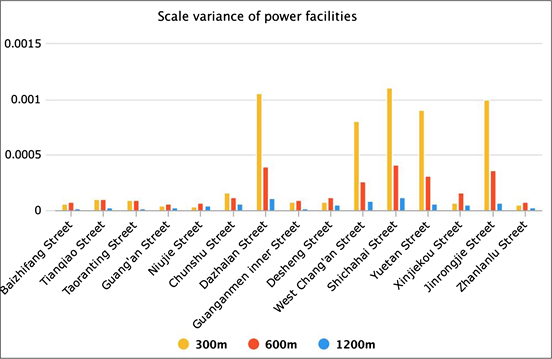
Figure 6 and Figure 7 show the variance distribution of the kernel density of each street at different scales for power facilities and traffic guardrail cases. It is obvious that the variance of kernel density decreases with the increase of scale. It shows that with the increase of scale, the kernel density value of each street area decreases. From (Figure 4(a), Figure 4(c), Figure 4(e)) and (Figure 5(a), Figure 5(c), Figure 5(e)), we can see that the larger the scale, the smaller the kernel density is, and the larger the concentrated area of the case distribution. Accordingly, the smoother the contour line changes, the smaller the variance is.
And it can be clearly seen that in the diagram that the maximum variance of kernel density in power facilities cases is at Shichahai Street, and in traffic guardrail cases it is at Dazhalan Street.
Figure 6. Power facilities variance comparison for kernel density of different streets and scales.
Figure 7. Traffic guardrail variance comparison of calculation results for kernel density of different streets and scales.
5. Conclusion
Urban grid management system has greatly improved the comprehensive efficiency of urban management. City infrastructure cases’ management is an important part of urban management. The analysis of urban management cases can present more useful information to improve the efficiency of case handling.
This paper focuses on the analysis of power facilities and traffic guardrail cases. It provides the hotspot information to intuitively display the spatial distribution trend of related cases, which can provide the management and resource deployment information for the relevant management departments. In the analysis of urban management cases, the choice of different scales reflects the different trend of cases distribution. The smaller the scale is, the more details reveals and the more concentrated areas are; The larger the scale is, the fewer concentrated areas and the larger concentrated area are, which highlights the overall distribution of cases. The larger the scale is, the smaller the density of urban management cases is; otherwise, the smaller the scale is, the larger the density of urban management cases is.
However, the spatial clustering method used in this paper belongs to the category of exploratory spatial data analysis in essence. It can assist in exploring the relationships, patterns and trends hidden in spatial data without excessive prior knowledge and assumptions, it can also handle other case types as listed in Table 1. In the future research, we plan to add population and economic variables and other auxiliary data, and use geographic weighted regression and other spatial statistical methods to do further modeling analysis.
Acknowledgements
This research is supported by the National Natural Science Foundation of China (No.41301489), Beijing Natural Science Foundation (No.4142013), BUCEA Post Graduate Innovation Project (No. PG2018061), Outstanding Youth Teacher Program of Beijing Municipal Education Commission (No.21147518308), Outstanding Youth Researcher Program of Beijing University of Civil Engineering and Architecture (No. 21082716012).
Conflicts of Interest
The authors declare no conflicts of interest regarding the publication of this paper.
Cite this paper
Hou, J. W., Liu, J. H., Li, S. Y., Song, S. R., Li, C. C., Duan, Y. M., & Zeng, B. S. (2018). The Spatial Distribution Pattern Analysis of City Infrastructure Cases of Urban Management. Journal of Geoscience and Environment Protection, 6, 21-42. https://doi.org/10.4236/gep.2018.612002
References
- 1. Zhao, C. X. (2012). Application of Urban Grid Management System. Science Mosaic. [Paper reference 1]
- 2. Dai, P., Jing, C., Du, M., & Zhou, W. (2015). A Method Based on Spatial Analyst to Detect Hot Spot of Urban Component Management Events. IEEE International Conference on Spatial Data Mining & Geographical Knowledge Services, Fuzhou, 8-10 July 2015, 55-59. https://doi.org/10.1109/ICSDM.2015.7298025 [Paper reference 1]
- 3. Fu, J. Y., Jing, C. F., Du, M. Y., Fu, Y. L., & Dai, P. P. (2017). Study on Adaptive Parameter Determination of Cluster Analysis in Urban Management Cases. ISPRS—International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, XLII-2/W7, 1143-1150. https://doi.org/10.5194/isprs-archives-XLII-2-W7-1143-2017 [Paper reference 1]
- 4. Fu, Q., Li, B., Yang, L. L. et al. (2015). Ecosystem Services Evaluation and Its Spatial Characteristics, in Central Asia’s Arid Regions: A Case Study in Altay Prefecture, China. Sustainability, 7, 8335-8353. https://doi.org/10.3390/su7078335 [Paper reference 1]
- 5. Gamez, R., & Ileana, L. (2012). New Perspectives on the Spatial Analysis of Urban Employment Distribution and Commuting Patterns: The Cases of Hermosillo and Ciudad Obregon, Mexico. Dissertations & Theses, Tucson, AZ: The University of Arizona. [Paper reference 1]
- 6. Gong, X., Cheng, H., Yang, L., Duan, Y., Yao, Y., Feng, Y. et al. (2017). Analysis of Geographical Distribution of Missing Children Based on the Missing Children Mobile GIS Mutual Assistance System of China. Journal of Geoscience and Environment Protection, 5, 117-134. https://doi.org/10.4236/gep.2017.512009 [Paper reference 1]
- 7. Hajduk, S. (2016). The Concept of a Smart City in Urban Management. Business Management & Education, 14, 34-49. https://doi.org/10.3846/bme.2016.319 [Paper reference 1]
- 8. Guo, J. et al. (2015). Urban Spatial Structure Based on Point Pattern Analysis—Taking Beijing Metropolitan Area as a Case. Economic Geography, 35, 68. [Paper reference 1]
- 9. Jing, C. et al. (2017). Spatial Pattern Analysis on Global Distribution of Urban Management Case Based on Nearest Index. Science of Surveying & Mapping, 42, 76. [Paper reference 2]
- 10. Kim, H. K., Yi, M. S., & Shin, D. B. (2017). Regional Diffusion of Smart City Service in South Korea Investigated by Spatial Autocorrelation: Focused on Safety and Urban Management. Spatial Information Research, No. 4, 1-12. https://doi.org/10.1007/s41324-017-0150-2
- 11. Leszek, K. (2015). Environmental and Urban Spatial Analysis Based on a 3D City Model. In Computational Science and Its Applications—ICCSA 2015 (pp. 633-645). Berlin: Springer International Publishing. https://doi.org/10.1007/978-3-319-21470-2_46 [Paper reference 1]
- 12. Li, M., & Zhou, Z. (2016). Positive and Negative Ecosystem Services Evaluation and Its Spatial Pattern Analysis on Urban Landscape: A Case Study of Xi’an City. Acta Geographica Sinica, 71, 1215-1230. https://doi.org/10.3724/SP.J.1006.2016.01215 [Paper reference 1]
- 13. Niemi, R., Rytkönen, E., Eriksson, R., & Nenonen, S. (2015). Scaling Spatial Transformation: Smart Specialization of Urban Capabilities in the Helsinki Region. Technology Innovation Management Review, 5, 42-51. https://doi.org/10.22215/timreview/936 [Paper reference 3]
- 14. O’Sullivan, D., & Wong, D. W. S. (2007). A Surface-Based Approach to Measuring Spatial Segregation. Geographical Analysis, 39, 147-168. https://doi.org/10.1111/j.1538-4632.2007.00699.x [Paper reference 1]
- 15. Okabe, A., Satoh, T., & Sugihara, K. (2009). A Kernel Density Estimation Method for Networks, Its Computational Method and a GIS-Based Tool. International Journal of Geographical Information Science, 23, 7-32. https://doi.org/10.1080/13658810802475491 [Paper reference 1]
- 16. Shen, L., & Guo, X. (2014). Spatial Quantification and Pattern Analysis of Urban Sustainability Based on a Subjectively Weighted Indicator Model: A Case Study in the City of Saskatoon, SK, Canada. Applied Geography, 53, 117-127. https://doi.org/10.1016/j.apgeog.2014.06.001 [Paper reference 1]
- 17. Wang, P., & Du, J. Q. (2014). Smart Cities and Urban Planning: An Analysis of Current Practices in Multiple Spatial Scales. City Planning Review, 38, 37. [Paper reference 1]
- 18. Zarabi, A., Saberi, H., Mohammadi, J., & Varesi, H. R. (2011). Spatial Analysis of Smart Growth Indicators (The Case Study: Regions of Isfahan). http://en.journals.sid.ir/ViewPaper.aspx?ID=259208 [Paper reference 1]
- 19. Zhu, J. (2006). Statistical Methods for Spatial Data Analysis. Publications of the American Statistical Association, 101, 389-340. https://doi.org/10.1198/jasa.2006.s66 [Paper reference 1]