Journal of Geoscience and Environment Protection
Vol.03 No.08(2015), Article ID:60181,13 pages
10.4236/gep.2015.38002
Enhancing Air Quality Forecasts over Catalonia (Spain) Using Model Output Statistics
Víctor Andrés Pérez1, Raúl Arasa1*, Bernat Codina1,2, Jesica Piñón1
1Technical Department, Meteosim S.L., Barcelona, Spain
2Department of Astronomy and Meteorology, University of Barcelona, Barcelona, Spain
Email: vperez@meteosim.com, *rarasa@meteosim.com, bcodina@meteosim.com, jpinon@meteosim.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 September 2015; accepted 6 October 2015; published 9 October 2015
ABSTRACT
Model Output Statistics (MOS) is a well-known technique that allows improving outputs from numerical atmospheric models. In this contribution, we present the development of a MOS algorithm to improve air quality forecasts in Catalonia, a region in the northeast of Spain. These forecasts are obtained from an Eulerian coupled air quality modelling system developed by Meteosim. Nitrogen Dioxide (NO2), Particulate Matter (PM10) and Ozone (03) have been the pollutants considered and the methodology has been applied on statistical values of these pollutants according to regulatory levels. Four MOS algorithms have been developed, characterized by different approaches in relation with seasonal stratification and stratification according to the measurement stations considered. Algorithms have been compared among them in order to obtain a MOS that reduces the forecast uncertainties. Results obtained show that the best MOS designed increases the accuracy of NO2 maximum 1-h daily value forecast from 71% to 75%, from 68% to 81% in the case of daily values of PM10, and finally, the accuracy of O3 maximum 1-h daily value from 79% to 87%.
Keywords:
Air Quality Modelling, Forecasting, Model Output Statistics (MOS)

1. Introduction
Air quality is one of the main issues that concerns current atmospheric research. Global air pollution has an impact on human health [1] , climate change [2] and on the physics and chemistry of the atmosphere [3] . Meteorological and air quality related environmental phenomena influence and limit the regional and urban development and safety management, which often leads to severe negative impacts on public health, economy and environment of polluted areas.
In Spain, annual average values of Nitrogen Dioxide (NO2) and Particulate Matter (PM10) are elevated in many urban air quality measurement stations with traffic influence [4] . Whereas, high ozone levels are measured in rural or suburban areas located downwind of urban or industrial locations and where local ozone precursors are lacking [5] [6] .The area of study is Catalonia (41.82˚N, 1.47˚E) in north-eastern Spain, in which six episodes with high levels of pollutants have been recorded in the last five years, thus making the Catalan Government adopt temporary mitigation measures. Figure 1 shows the topographical features of Catalonia. Black dots point the four provinces that divide the studied area.
For these reasons, it will be desirable that public administrations may count on tools which enable them to anticipate the potential risks caused by pollution, helping the management of health, economical and environmental impacts that may affect the polluted areas of its population. In this sense, models are a very useful tool for local administrations for planning and managing production, human resources, activities and emergency procedures; and to introduce improvement plans of air quality urban areas. Nowadays, coupled Eulerian air quality models are useful tools to manage air pollution, and they can even complement or replace air quality monitoring in terms of what the European Directive establishes.
Despite years of refinements and improvements, meteorological and air quality models still contain significant errors. Several statistical techniques have been designed and applied in the last few years [7] -[12] in order to reduce the uncertainty of their forecasts. In this work, we focus on the use of the Model Output Statistics (MOS) technique to improve forecasts obtained by an air quality modelling system. MOS has been applied usually to meteorological applications [13] -[17] but there are a few applications on air quality [18] -[20] . Air quality forecasts have been obtained by a coupled Eulerian air quality modelling system developed by Meteosim [21] . This coupled air quality modelling system has been applied and tested successfully in urban (Madrid or Barcelona in Spain; Nice in France) and industrial areas (Ponferrada or Tarragona in Spain). This air quality modelling system has been evaluated using Maximum Relative Directive Error [22] referred in the European
Figure 1. Topographical features of Catalonia.
Directive EC/2008/50. Results obtained from this evaluation accomplish the model uncertainty limits according to the Directive for the pollutants O3, NO2, PM10, SO2 and CO, having used measurements from more than 120 stations (urban, suburban and rural locations) during a period of three years.
The MOS technique has been applied to daily values of NO2 and PM10, maximum 1-h daily values of NO2 and O3 and maximum 8-h daily values of O3 forecasted over Catalonia (Spain). Air quality measurement data have been provided by the Air Quality Network that belongs to the Territory and Sustainability Department of the Catalonian Government. The study includes a numerical deterministic evaluation that shows the accuracy of the air quality modelling outputs with and without the MOS technique.
Description of the model output statistics technique and the uncertainty evaluation methodology are presented in section 2; a detailed analysis of the results obtained is presented in section 3; and finally, some conclusions are reported in section 4.
2. Methodology
2.1. Model Output Statistics
The technique Model Output Statistics (MOS) computes regression equations between observed and model forecasted variables. These equations are later applied to the raw model output to get a modified and statistically corrected output.
This technique requires a set of variables from the modelling system to be corrected and a set of observed variables. These datasets cover a time period known as training period. Its length is variable but it is advisable to have the longest possible period to include potential cycles. In this work we have used the period comprised between the 24th of October 2012 and the 31st of August 2013, which includes 720,000 hourly values.
Within the MOS correlation equations we distinguish between predictands and predictors. The predictant is the dependent variable to be forecasted or corrected. In developing our MOS, the predictants will be the statistics described in the introduction: maximum 1-h value and daily values for NO2, daily value for PM10 and maximum 1-h and 8-h values for O3.
The predictors are the independent variables of the regression equations. In this work, we have used the concentration values forecasted by the modelling system. Since we have only used one predictor, we will omit the discussion about predictor-selection algorithms [23] -[27] . It is worth mentioning that in a preliminary phase we did test the viability of using more predictors, such as hourly data and its derived statistics, as well as past observational data. However, we finally found out that the use of the statistics of each pollutant as obtained by the modelling system produced the best results.
Often, the datasets employed in the regression equations are grouped in order to optimize the forecasting relationships and improve the precision of the MOS technique. This grouping is usually referred to as data stratification.
2.2. Error Statistics
In order to evaluate the potential improvements of the MOS technique on the modelling system, we will use a numerical validation. Several statistics will be used for the error measurement of the differences between results obtained with and without MOS. Most of them are typical statistics employed in error evaluation in meteorological models [22] [28] and, in particular, in air quality models [29] -[31] . Reference [32] draws some recommendations on the maximum thresholds for some of these statistics in the analysis and forecast of pollutant concentrations1 that we will use in this work.
In the next definitions, n is the sample size, oi and fi the observed and forecasted values, where i Î [1, n]:
Mean normalized error:
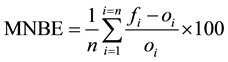 (1)
(1)
Reference [32] recommendation: MNBE < ±15%.
Mean normalized gross error:
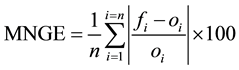 (2)
(2)
Reference [32] recommendation: MNGE < 35%.
Index of agreement:
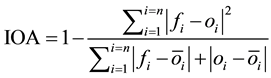 (3)
(3)
This is a statistic to evaluate with a single value the goodness of fit of a modelling system with respect to the observations. As close as one is the value, the best is the fit; and it worsens as it approaches to zero.
2.3. Forecast Evaluation
Table 1 shows a summary of the errors of the modelling system in the training period using the above described statistics.
As can be seen, most of the statistics fall within [32] recommendations, with the exception of the values of the PM10 pollutant. The presence of these errors, however, justifies the need of developing a MOS.
2.4. Description of the Proposed MOS Categories
From the observed and modelled data, we have proposed two kinds of stratifications:
・ A seasonal stratification. The analysis of observed concentration exhibits a dependency on temperature, especially remarkable for ozone, which suggests splitting the training stage in 4 different periods. At first glance one could think that a natural division would involve climatologically seasons, but the study of mean temperature and concentration of the considered pollutants show that this division is not appropriate. We have finally chosen a division in training periods in which the values of temperature and pollutants change significantly from one to another (Figure 2 and Table 2).These periods turned to be 23 Oct 2012 to 02 March 2013 (defined as Period 1), 03 March 2012 to 01 May 2013 (defined as Period 2), 02 May 2013 to 06 July 2013 (defined as Period 3) and 07 July 2013 to 31 August 2013 (defined as Period 4).Stratification according to the measurement station in order to identify systematic errors and biases of each measurement point.
・ Stratification according to the measurement station in order to identify systematic errors and biases of each measurement point.
Table 1. Summary of the errors of modelling system in the training period.
Table 2. Average maximum hourly and daily values of NO2, daily value of PM10 and maximum hourly and 8-hourly values of O3 within each period.



Figure 2. Average daily time evolution of concentration values of NO2 (a) PM10 (b) and O3 (c) for the considered periods.
A total of 2 × 2 separations have been done, yielding to 4 different categories. Table 3 shows a summary of the categories and the nomenclature that will be used.
3. Results
In this section we analyze the errors resulting from applying a period-specific trained MOS on the modelling output system. We use the deterministic numerical validation, the comparison between mean daily evolutions, and the comparison of the frequency histograms of the average errors of each category as well as the parameters of a Gaussian fit. This will allow us to choose the best MOS for each pollutant and statistics.
3.1. NO2
Table 4 shows the error analysis statistics of the different categories after having been applied to the modelling system of the NO2 pollutant. Figure 3 shows a comparison between normalized mean absolute errors in each category.
Table 4 and Figure 3 show that MOS E C produces the best results for both the maximum hourly value and the daily value. Notice that MOS 0 and MOS C do not improve the modelling system.
In case of the maximum hourly value, MOS E C reduces MNBE from 11.7% to 9.5% of the modelling system, reduces MNGE from 29.5% to 24.3%, and increases IOA from 0.86 to 0.91.
For the daily value, MOS E reduces MNBE from 11.8% to −0.9%, thus correcting the overestimation of the modelling system, reduces MNGE from 24.9% to 18.1%, and increases IOA from 0.91 to 0.95.
The frequency histograms of Figure 4(a) and Figure 4(b) have been created to better analyze the improvements of the different categories. These histograms display the error distributions of the modelling system and of
Table 3. Summary of the proposed MOS categories.
Table 4. Errors of all MOS categories as well as NO2 forecasting system.
Figure 3. Comparison of MNGE and MNBE between the different MOS categories and the NO2 modelling system for maximum 1-h value [left] and daily value [right].


Figure 4. Histograms of error distributions in the evaluation of the modelling system and the MOS categories for maximum hourly values (a) and daily values (b) of NO2.
maximum hourly values and daily values for each MOS category. Obviously, better results are associated to centred and peaked distributions.
As can be seen, the error distributions of both MOS E and MOS E C are the sharpest and narrowest and so the best. For daily values, the best results are attained by MOS E C but closely followed by the rest.
Through a Gaussian fit, we have calculated the width (twice the standard deviation) and displacement of the distributions with respect to the origin. The results are presented in Table 5. MOS E features a near zero shift and the narrowest width and MOS E C features the smallest displacement and width for daily values among all categories.
Figure 5(a) let us compare the time evolution of the mean daily values of observed maximum hourly values of NO2 with those forecasted by the modelling system and those corrected by MOS E C. And Figure 5(b) shows the same comparison for daily values.
Paying attention at the behaviour of the errors on measurement stations we see that, in general, the improvement introduced by MOS E C is quite apparent in the maximum 1-h values, exhibiting generalized reductions in MNBE and MNGE and increases in IOA. MOS E C reduces MNBE in 78% of the measurement stations and 88% exceed [32] acceptance criteria for both MNBE and MNGE, which turned out to be only 69% and 75%, respectively, with the raw modelling system. On the other hand, the improvement produced by MOS E C over the modelling system in daily values is also very clear, reducing MNBE in 88% of measurement stations. Moreover, all stations exceed [32] acceptance criteria while 69% and 89% did, respectively, with the raw modelling system.
Table 5. Parameters of the Gaussian fit of the different MOS categories with respect to the maximum hourly value and daily value of NO2.


Figure 5. Time evolution of mean daily values of observed maximum hourly values of NO2 (a) and observed daily values (b) forecasted by the modelling system and corrected by MOS E C in the training period.
3.2. PM10
Table 6 shows the error analysis statistics of the different categories applied to the output of the modelling system of pollutant PM10. Figure 6 displays the comparison between normalized mean absolute errors.
It can be seen that the best results are obtained with MOS E C. It decreases the underestimation produced by the modelling system, reducing MNBE from −24.2% to 5.9%, MNGE from 32.1 to 19.3% and increases IOA from 0.75 to 0.91.
Figure 7 displays frequency histograms of the mean error distributions in forecasting daily values for different MOS categories and the modelling system. Table 7 shows the parameters of the Gaussian fit.
The results are very similar for categories MOS E and MOS E C for which the curves are narrower and centred.
To further show the improvement introduced by MOS E C, Figure 8 shows the comparison between the time evolution of daily PM10 values observed, forecasted by the raw modelling system and corrected by MOS E C.
Focusing on the impact of MOS E C at the measurement stations, it can be seen that MOS E C diminishes MNGE in all of them. Moreover, all measurement stations exceed [32] acceptance criteria for MNBE and MNGE, which is a very good achievement since only 21% and 58%, respectively, of the stations, satisfied the criteria with just the modelling system.
Table 6. Errors of all MOS categories as well as PM10 forecasting system.
Table 7. Parameters of the Gaussian fit of the different MOS categories with respect to the daily value of PM10.
Figure 6. Comparison of MNGE and MNBE between the different MOS categories and the PM10 modelling system.
Figure 7. Histogram of error distributions in the evaluation of the modelling system and the MOS categories for daily values of PM10.
Figure 8. Time evolution of daily PM10 values observed, forecasted by the modelling system and corrected by MOS E C in the training period.
3.3. O3
Table 8 shows the error analysis statistics of this pollutant for the different categories and Figure 9 the comparison among the mean normalized errors.
As can be seen, MOS E C gets the best results, both in the maximum hourly value and maximum 8-hourly.
In the maximum hourly value, MOS E C slightly increases the MNBE of the modelling system from 1.8% to 2.8%, reduces MNGE from 20.8% to 13.2%, and increases IOA from 0.62 to 0.91.
For the maximum 8-h value, MOS E C reduces the MNBE of the modelling system from 7.0% to 3.9%, MNGE from 25.3% to 15.5%, and increases IOA from 0.68 to 0.92.
Figure 10 displays the mean error distributions of the forecasts of the values for every MOS category and the modelling system and Table 9 summarizes the errors of the Gaussian fit.
The best results are attained by MOS C and MOS E C, especially the former, for the maximum hourly value. MOS C produces the narrowest curve followed by MOS E C, though they are not quite centred. For the maximum 8-hourly value, the best results are attained by MOS E C followed by MOS C. MOS E C has the smallest width but is not the best centred.
Table 8. Errors of all MOS categories as well as O3 forecasting system.
Table 9. Parameters of the Gaussian fit of the different MOS categories with respect to the maximum 1-hourly value and maximum 8-hourly value of O3.
Figure 9. Comparison of MNGE and MNBE between the different MOS categories and the O3 modelling system for maximum 1-h value [left] and maximum 8-h value [right].

Figure 10. Histograms of error distributions in the evaluation of the modelling system and the MOS categories for maximum 1-hourly values (a) and maximum 8-hourly values (b) of O3.
The improvements achieved by MOS E C are further analyzed in Figure 11(a) and Figure 11(b) which compare the evolution of the averaged maximum 1-h and 8-h values of O3 forecasted by the modelling system and corrected by MOS E C.
The analysis of errors by measurement stations show that the improvement introduced by MOS E C over the modelling system for maximum hourly values is apparent for most of the stations, with a generalized reduction of MNBE and MNGE, and an increase of IOA. MOS E C reduces MNGE in all stations and, moreover, all of them end up verifying [32] acceptance criteria for MNBE and MNGE.
Furthermore, the improvements produced by MOS E C over the modelling system, in case of the maximum 8- hourly value, are also generalized, with reductions in both MNBE and MNGE and increases in IOA. MOS E C reduces MNBE in all measurement stations and [32] criteria are met in all of them for MNBE and MNGE. This compares to 76% and 81%, respectively, of the measurement stations that met the criteria with the raw modelling system.
4. Conclusions
In this paper, we have applied the well-known MOS methodology in air quality modelling, a field where this tech-


Figure 11. Time evolution of averaged maximum 1-hourly values (a) and maximum 8-hourly values (b) of O3 observed, forecasted by the modelling system and corrected by MOS E C in the training period.
nique is rarely employed. The output of an Eulerian coupled air quality modelling system feeds 4 MOS categories for each of these 5 statistics: maximum 1-h daily value and daily values of NO2, daily values of PM10 and maximum 1-h and 8-h daily value of O3; this amounts to 20 MOS considered.
The best results for all statistics have been obtained with the category that stratifies by measurement stations and by periods, as expected. The stratification by measurement stations corrects systematic errors of the modelling system. The stratification by periods allows for the treatment of the seasonal dependency of concentration values.
In summary, the application of the MOS methodology increases the accuracy of the maximum 1-h daily value of NO2 from 71% to 75%, the daily value of NO2 from 75% to 82%, the daily value of PM10 from 68% to 81%, the 1-h daily value of O3 from 79% to 87% and the 8-h daily value of O3 from 75% to 85%.
Our results highlight the improvements achieved by a quite simple mathematical tool with a very low computational cost. MOS methodology only increases a 2% the total computational cost of the operative air quality modeling system, and provides an improvement between 3% and 10% of the air quality forecasts. Nevertheless, one cannot forget that the MOS implementation should go in parallel with enhancements in the modelling system such as introducing better pollutants emission values to the modelling system. Any changes in the modelling system, however, imply the recalculation of the MOS regression coefficients.
Acknowledgements
This work was funded by the Catalan Government and the Spanish Government through the projects PTOP- 2013-608 and PTQ-12-05244 respectively. The authors gratefully acknowledge the technicians at the Territory and Sustainability Department of the Catalonian Government for providing air quality measurements.
Cite this paper
Víctor AndrésPérez,RaúlArasa,BernatCodina,JesicaPiñón, (2015) Enhancing Air Quality Forecasts over Catalonia (Spain) Using Model Output Statistics. Journal of Geoscience and Environment Protection,03,9-22. doi: 10.4236/gep.2015.38002
References
- 1. Newby, D.E., Manucci, P.M., Grethe, S.T., Baccarelli, A.A., Brook, R.D., Donaldson, K., Forastiere, F., Franchini, M., Franco, O.H., Graham, I., Hoek, G., Hoffmann, B., Hoylaerts, M.F., Künzli, N., Mills, N., Peklanen, J., Peters, A., Piepoli, M.F., Rajagopalan, S. and Storey, R.F. (2014) Expert Position Paper on Air Pollution and Cardiovascular Disease. European Heart Journal, in Press.
http://dx.doi.org/10.1093/eurheartj/ehu458 - 2. Crutzen, P.J. (2004) New Directions: The Growing Urban Heat and Pollution Island Effect-Impact on Chemistry and Climate. Atmospheric Environment, 38, 3539-3540.
http://dx.doi.org/10.1016/j.atmosenv.2004.03.032 - 3. Ritter, M., Müller, D., Tsai, M.-Y. and Parlow, E. (2013) Air Pollution Modeling over Very Complex Terrain: An Evaluation of WRF-Chem over Switzerland for Two 1-Year Periods. Atmospheric Research, 132-133, 209-222.
http://dx.doi.org/10.1016/j.atmosres.2013.05.021 - 4. Querol, X., Viana, M., Moreno, T. and Alastuey, A. (2012) Bases científico-técnicas para un Plan Nacional de Mejora de la Calidad del Aire. Consejo Superior de Investigaciones Científicas (CSIC).
- 5. Soler, M.R., Hinojosa, J., Bravo, M., Pino, D. and Vila, J. (2004) Analyzing the Basic Features of Different Complex Terrain Flows by Means of a Doppler Sodar and a Numerical Model: Some Implications to Air Pollution Problems. Meteorological Atmospheric Physics, 85, 141-154. http://dx.doi.org/10.1007/s00703-003-0041-z
- 6. Aguirre-Basurko, E., Ibarra-Berastegui, I. and Madariaga, I. (2006) Regression and Multilayer Perceptron-Based Models to Forecast Hourly O3 and NO2 Levels in the Bilbao Area. Environmental Modelling Software, 21, 430-446.
http://dx.doi.org/10.1016/j.envsoft.2004.07.008 - 7. McKeen, S., Wilczak, J. and Grell, G. (2005) Assessment of an Ensemble of Seven Real-Time Ozone Forecasts over Eastern North America during the Summer of 2004. Journal of Geophysical Research D, 110, Article ID: D21307.
- 8. Wilczak, J.M., McKeen, S. and Djalalova, I. (2006) Bias-Corrected Ensemble and Probabilistic Forecasts of Surface Ozone over Eastern North America during the Summer of 2004. Journal of Geophysical Research D, 111, Article ID: D23S28.
http://dx.doi.org/10.1029/2006jd007598 - 9. Delle Monache, L., Nipen, T., Deng, X., Zhou, Z. and Stull R. (2006) Ozone Ensemble Forecasts: 2. A Kalman Filter Predictor Bias Correction. Journal of Geophysical Research D, 111, Article ID: D05308.
- 10. Kang, D., Mathur, R., Rao, S.T. and Yu, S. (2008) Bias Adjustment Techniques for Improving Ozone Air Quality Forecasts. Journal of Geophysical Research, 113, Article ID: D23308.
- 11. Djalalova, J., Wilczak, J., McKeen, S., Grell, G., Peck-Ham, S., Pagowski, M., DelleMonache, L., McQueen, J., Tang, Y., Lee, P., McHenry, J., Gong, W., Bouchet, V. and Mathur, R. (2010) Ensemble and Bias-Correction Techniques for Air Quality Model Forecasts of Surface O3 and PM2.5 during the TEXAQS-II Experiment of 2006. Atmospheric Environment, 44, 455-467.
http://dx.doi.org/10.1016/j.atmosenv.2009.11.007 - 12. Arasa, R., Soler, M.R. and Olid, M. (2012) Numerical Experiments to Determine MM5/WRF-CMAQ Sensitivity to Various PBL and Land-Surface Schemes in North-Eastern Spain: Application to a Case Study in Summer 2009. International Journal of Environment and Pollution, 48, 105-116.
http://dx.doi.org/10.1504/IJEP.2012.049657 - 13. Dallavalle, J.P., Ericksonv, M.C. and Maloney, J.C. (2000) Model Output Statistics (Mos) Guidance for Short-Range Projections. National Weather Service/NOAA.
- 14. Nicolis, C. and Vannitsem, S. (2007) Dynamical Properties of Model Output Statistics Forecasts. Institute Royal Meteo-rologique de Belgique, Brussels.
- 15. Glahn, B., Peroutka, M. and Wiedenfeld, J. (2008) MOS Uncertainty Estimates in an Ensemble Framework. NOAAN, Wakeld, VA.
- 16. Monarski, A. (2011) Verification of Model Output Statistics Forecasts Associated with the North American Mesoscale Model Upgrade. Master’s Scholarly Paper, Department of Atmospheric and Oceanic Science, University of Maryland, College Park.
- 17. Ranaboldo, M. (2011) Multiple Linear Regression MOS for Short-Term Wind Power Forecast. Universitat de Barcelona, Barcelona.
- 18. Karl, T.R. (1978) Potential Application of Model Output Statistics to Forecast of Surface Ozone Concentrations. National Meteorological Center’s Limited Area.
- 19. Jianming, X. and Xiangde, X. (2010) Study of Statistically Correcting Model CMAQ-MOS for Forecasting Regional Air Quality. Nanjing University of Information Science Technology, Nanjing.
- 20. Pijnappel, A. (2011) Statistical Post Processing of Model Output from the Air Quality Model LOTOS-EUROS. De Bilt, Stageverslag.
- 21. Arasa, R., Picanyol, M. and Solé, J.M. (2013) Analysis of the Integrated Environmental and Meteorological Forecasting and Alert System (SIAM) for Air Quality Applications over Different Regions of the Iberian Peninsula.
http://www.harmo.org/Conferences/Proceedings/_Madrid/downloadItem.asp?CID=H15-70 - 22. Denby, B. (2010) Guidance on the Use of Models for the European Air Quality Directive. A Working Document of the Forum for Air Quality Modelling in Europe FAIR-MODE, ETC/ACC Report.
- 23. Miles, J. and Shelvin, M. (2001) Applying Regression Correlation. Sage Publications, London.
- 24. Pérez López, C. (2003) Estadística. Problemas resueltos y problemas. Editorial Pearson.
- 25. Wilks, S.D. (2006) Statistical Methods in the Atmospheric Sciences. Second Edition, Academic Press, Waltham.
- 26. Montgomery, D.C., Peck, E.A. and Vining, G.G. (2011) Introducció al Análisis de Regressión Lineal. Grupo Editorial Patria. Tercera edición.
- 27. Chatterjee, S., Hadi, A.S. and Price, B. (2012) Regression Analysis by Examples. Fifth Edition, Wiley Series in Probability and Statistics.
- 28. Willmott, C.J., Ackleson, S.G., Davis, R.E., Feddema, J.J., Klink, K.M., Legates, D.R., O’Donnell, J. and Rowe, C.M. (1985) Statistics for the Evaluation and Comparison of Models. Journal of Geophysical Research, 90, 8995-9005.
- 29. EPA (2009) Reassessment of the Interagency Workgroup on Air Quality Modeling (IWAQM) Phase 2 Summary Report: Revisions to Phase 2 Recommendations. Draft for Internal Review. US EPA Report No. EPA-454/R-09-XXX, Office of Air Quality Planning and Standards, Research Triangle Park, North Carolina.
- 30. Arasa, R. (2010) Avaluació del rendiment del sistema de modelització MM5/MNEQA/CMAQ de la qualitat de l’aire per a pronosticar l’ozó a Catalunya. Tethys núm. 7.
- 31. Arasa, R. (2011) Modelització i simulació fotoquíimica mesoescalar del transport del material particular i gasos a l’atmosfera. Tesis doctoral, Universitat de Barcelona, Barcelona.
- 32. EPA (1991) Guideline for Regulatory Application of the Urban Airshed Model. US EPA Report No. EPA-450/4-91-013. Office of Air and Radiation, Office of Air Quality Planning and Standards, Research Triangle Park, North Carolina.
- 33. EPA (2005) Guidance on the Use of Models and Other Analyses in Attainment Demonstrations for the 8-Hour Ozone NAAQS. US EPA Report No. EPA-454/R-05-002, Office of Air Quality Planning and Standards, Research Triangle Park, North Carolina.
NOTES
*Corresponding author.
1Although [33] states that a rigid criterion to accept or reject a model would be inadequate, according to [33] a range of values could be used as indicators of the goodness of a model.











