Voice of the Publisher
Vol.01 No.03(2015), Article ID:61716,11 pages
10.4236/vp.2015.13009
Clusters―The Seeds of Droplets and Snowflakes
Boris Sedunov
Russian New University, Moscow, Russia

Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 9 October 2015; accepted 1 December 2015; published 4 December 2015

ABSTRACT
The clusters play a significant role in formation of Universe, in the condensation of matter and meteorological phenomena, in processes of life, and in our technologies. Therefore, they should be studied better. Modern electronic thermophysical databases are very rich sources of knowledge about cluster properties. This research is directed towards development and perfection of methods to extract properties of clusters from precise thermophysical data. The parallel between clusters, droplets and snowflakes helps in this investigation. The paper shows the achievements and discoveries on this way. The soft structural transition in cluster fractions is opposed to the abrupt phase transition at a condensation of matter.
Keywords:
Real Gas, Cluster, Isomer, Molecular Interaction, Bond Energy, Equilibrium Constant, Nucleation, Condensation, Structural Transition, Heat Capacity, Potential Energy

1. Introduction
We are surrounded by invisible nanosized objects, which at a change of external conditions become transformed in visible droplets, snowflakes, crystallites, dust clouds, planets and stars. These objects are clusters of molecules joined together by weak intermolecular forces. In gardens or fields the clusters bring us fragrance of flowers. In a hot day the clusters of water bring us freshness, but in a humid winter day they make us suffer from extra cold. In a living cell the macromolecular clusters perform the miracle of life. They are not as strongly bound and stable as chemical substances, but it does not make them less influential. They enter the signal chain of a cell and easily change their structure under slight external influences and temperature changes.
The clusters are as multiple as chemical compounds and they strongly influence the properties of real gases. The scientists and technologists have to take into account clusters in their research works and technological processes. Moving step by step from ideal to denser gases we observe transformations of clusters from tiny two-particle complexes, named dimers, to larger n-particle agglomerations [1] [2] , which become visible, if growing to a size in a micrometer range.
It is difficult to investigate properties of equilibrium clusters experimentally. Nanosized dimensions of clusters require extra short wave radiation to study their structure. But the energy of short wave quanta greatly exceeds weak bond energies of clusters, and the radiation destroys clusters to be studied. Here we see an analogy with the investigation of biological objects: too strong experimental interventions in living cells kill them, thus preventing the mystery of life from discovery. But to investigate the clusters’ structure and properties we can use statistical methods [3] [4] . Huge statistics of cluster populations in real gases imprints their properties in thermophysical properties of real gases and thus makes them measurable [5] .
This paper is based on the computer aided analysis of precise thermophysical data for pure real gases, contained in the NIST (National Institute of Standards and Technology, USA) Thermophysical Properties of Fluid Systems Database [6] . Nowadays a large number of experimental data, produced by researchers from all over the world, have been concentrated in electronic databases, thus making them accessible for scientists and practitioners. This process includes a careful selection of experimental data and their generalization based on well established laws of nature [7] . The high precision of electronic databases permits to extract hidden properties of clusters and molecular interactions [8] via computer processing of experimental data [5] . This high precision of data helps to overcome the inverse problem results divergence [9] at searching for hidden parameters. By this way the electronic databases become perfect sources of knowledge about fundamental properties of matter. With time the creation and utilization of electronic databases will develop in a powerful direction of science and technology.
In this research an advanced method [5] for computerized analysis of precise thermophysical data had been developed based on extension of the thermodynamics and thermal physics laws for pure real gases. The method uses series expansion of precise thermophysical functions by the monomer fraction density [10] . The developed method helps to discover unknown properties of clusters and molecular interactions in molecular [11] and atomic [12] gases and in supercritical fluids [13] - [16] . In this paper we pay attention to polar gases, such as the water and methanol vapors, which at low temperatures possess tetramers with giant bond energies and strong orientation of hydrogen bonds. This extra high orientation of bonds and their enlarged bond energies inspire the idea about a new mechanism of intermolecular bonding in this case.
2. Clusters in Nature
2.1. The Clusters in Space
According to the generally accepted theory, at first steps of the Universe development it was in a plasma state with ionized atoms and free moving electrons. The expansion of the young Universe led to its cooling that resulted in a formation of neutral atoms. The temperature of Universe is far from uniform: some regions, such as centers of stars, stay extra hot, but other regions become cold enough to permit the formation of molecules. At a further expansion the thermal movement energy in less hot regions becomes low enough to permit the formation of weakly bound molecular clusters. Clusters in the Universe are essential in those gaseous and fluid regions, where the temperature does not exceed two thousands of Kelvins. At a further growth of temperature the dissociation of molecules and ionization of atoms changes the picture.
The clusters in galactic gaseous clouds are nuclei and seeds for the growth of crystals of solid or droplets of liquid matter. The lower is the temperature, the more clusters may be merged together to form solid or liquid visible particles of the galactic dust clouds. Huge dust clouds may give birth to asteroids, new stars and their planets. So, starting from clusters, we come to the formation of stars and planets. The development of infrared spectroscopy may give information about processes of clusters growth and merging in galactic dust clouds.
2.2. Clusters as Nucleation Centers
A lot of attention in scientific literature is attracted to the nucleation problem [17] . It means the process of large enough clusters creation in a supersaturated medium, which can serve as nuclei and grow in this medium leading to the phase transition. This problem is essential for the vapor-fog transformation and growth of clouds in a supersaturated vapor; crystallization in a supercooled liquid and in a supersaturated solution; formation of aerosols in atmosphere and trails after jets; formation of galactic clouds, and so on. Frequently, some agents, such as dust, are supposed to play the role of seeds. For example, in the jet trail formation it is supposed that the soot in the jet engine exhaust may serve as the seed. But our analysis of 1D chain clusters [18] shows that even in under saturated vapor the length of linear clusters may be very large. So, at a super saturation the extra long clusters may serve as nuclei for further condensation of vapor.
2.3. The Clusters of Water in the Earth Atmosphere
The most remarkable clusters in the Earth atmosphere are clusters of Water. The evaporation of Water from wet or liquid parts of the Earth surface creates the upstream of hot and humid air in a cyclonic region. The lifting air cools with height, thus creating favorable conditions for joining molecules of Water in small clusters. When we observe white clouds in the blue sky, such as shown at the Figure 1, we may think that the Water molecules are concentrated only in clouds. That is not so. The blue regions between clouds contain almost the same concentration of Water molecules, but this Water is accumulated in invisible tiny clusters, which dimensions are small as compared to the wavelength of the visible range of light.
The same process takes place in a cold morning after a rainless night. The grass and flowers become covered with dew, formed from small Water clusters, Figure 2. When temperature falls, the saturation density of Water vapor may become lower than the real density of vapor. Then the excess of Water molecules, concentrated mainly in the largest clusters of the vapor, merge in droplets of dew that fall on grass and flowers. So, clusters behave as nuclei for the dew droplets.
In winter, instead of dew, we can see a frost on grass and branches made of smallest snowflakes. In Siberia or Alaska in a cold winter day the breathing creates a white cover of frost around mouth and nose, on eyelashes, eyebrows, moustaches, beard, and a fur hat. The origin of the frost is the same as of dew, but at temperatures lower than zero degrees Celsius.
Figure 1. The clouds with blue zones between them filled with invisible Water clusters.
Figure 2. The droplets of dew on flowers, formed from clusters of Water molecules.
A very interesting picture we may see behind the jet plane. Very frequently the flight of jets is accompanied by white traces that decorate all sky for a long time. In other conditions the trails are short, with quickly disappearing ends. The origin of these traces is the same as the origin of frost: the formation of visible snowflakes from invisible clusters, contained in the hot and humid jet engine exhaust. The duration of traces depends on the initial concentration of water molecules in cold atmosphere at the height of the airplane flight. When the concentration is oversaturated, the white trail stays for a long time. When the concentration is much smaller than the saturation one, the visible trail disappears quickly, leaving for some time an invisible trace of clusters. Here again the progress in the spectroscopy may make the rests of trails visible.
To understand different structural forms of invisible clusters we can use the analogy with macroscopic visible forms of molecular complexes. The macroscopic complexes of Water molecules may be in two different forms: solid in snowflakes and liquid in droplets, Figure 3.
The same may be stated for nanosized clusters: at low temperatures they are solid-like, but at elevated temperatures the cluster structure becomes more flexible and liquid-like, with a smaller strength and number of bonds between molecules. The developed by the author computerized analysis of precise thermophysical data throws the light on this interesting transformation [1] [5] .
We may feel the presence of Water clusters in air by our skin. The unbound in clusters molecules (monomers) do not heat or cool our skin: they bring some heat and take it away at the evaporation. When a cluster comes to our skin and then is spread away in a form of monomers, it receives from our body the energy needed for its dissociation. The Water molecules in clusters are joined together due to the cluster bond energy. It is the total energy of all intermolecular bonds in a cluster. So, if the air contains clusters, we feel a cooling effect. In summer this effect may be pleasant, but in winter a wet air makes us suffer from an extra cold produced by clusters. The presented here method [5] provides computation of the clusters’ bond energies [1] [11] and thus permits to estimate the cooling effect of clusters penetrating through our clothes.
We may feel the effect of clusters in the perfume of air. And we enjoy wonderful dishes prepared by steaming. It was shown by the author [16] that clusters of Water can dissolve volatile components of a condensed matter. Therefore, in wet air, filled with Water clusters, there are more chances for fragrances to be extracted from flowers rather than in a dry air. So, high humidity of air is favorable to enjoy aroma of gardens or fields. The extraction of aromatic substances from leaves and flowers based on clusters of real gases may possess advantages, such as better selectivity of fragrances.
2.4. The Clusters in Living Cells
The hard, liquid and gaseous spheres of Earth with their temperature around 300 K are favorable both for life and for clusters formation. We dare say that the life itself benefits from transformations of clusters, which do not require too much of energy as compared to chemical transformations. The smallest changes in temperature or chemical potentials of basic components result in structural transformations of macromolecular clusters in a living cell. It may be one of basic mechanisms of the living cell functioning. So, to discover the mystery of life we should understand better the molecular interactions [8] reflected in the clusters’ structure and properties.
This investigation of clusters starts from the simplest pure real gases just to build the foundation for the total cluster theory. We will move step-by-step from the smallest clusters, dimers and trimers in diluted gases, to larger clusters in denser gases and even in supercritical fluids.
Figure 3. A snowflake and a droplet formed from water clusters at different temperatures.
3. A Brief Description of the Method
3.1. The System of Equations for Density and Pressure of a Pure Gas
The developed computer aided analysis of precise thermophysical data [5] is based on the series expansion of thermophysical functions by the Monomer fraction density Dm [10] . This variable means the density of basic particles of a pure monocomponent gas in zones, where they are free from interactions with other particles of a gas. Basic particles of a pure gas are all chemically identical particles, independently on their inclusions in clusters. The thermophysical properties of pure gases and fluids in the NIST database [6] are referred to a mole of basic particles.
From a microscopic point of view it seems to be difficult to select these zones and calculate the density of monomers. But Thermodynamics opens a wonderful possibility [10] [11] to find the monomer fraction density Dm from the known isothermal dependence of the total density of basic particles D on pressure P:
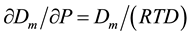 (1)
(1)
The Figure 4 shows, how the total density of basic particles D differs from the monomer fraction density Dm and from the density of free moving particles Dp = P/RT (ideal gas density).
The density D is the total molar density of all basic particles of a gas, independently on their inclusions in different cluster fractions. The ideal gas density, Dp = P/RT, is the density of all free moving particles: monomers and clusters, independently on numbers of basic particles in clusters, at pressure P. The monomer fraction density is the density of basic particles not included in clusters in zones, where every of these particles does not interact with other particles. The density of clusters in the n-particle cluster fraction corresponds to the mass action law [19] and is equal to:
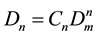 (2)
(2)
where Cn is the coefficient of the n-order term of Dp = P/RT series expansion by Dm, C1 = 1. But the series expansion cannot separate contributions of different isomers of the n-particle clusters. So, Dn is the total density of all isomers at the same number of particles in the cluster fraction.
At low pressures the three densities almost coincide. It means that the gas tends to ideal behavior, at which almost all basic particles are included in the Monomer fraction. But at high pressures we see the divergence of these three densities. The pressure is not more the partial pressure of the Monomer fraction, but is summed with partial pressures of cluster fractions. The density D sums partial densities of the monomer and all cluster fractions. It is reflected [10] [11] in the system of Equations (3) and (4) for D and P, with Dn given by Equation (2).
 (3)
(3)
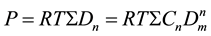 (4)
(4)
Figure 4. Density (blue line), ideal gas density at pressure P, Dp = P/RT (red line), monomer fraction density Dm (green line) versus pressure in the Water vapor at T = 610 K.
3.2. The Potential Energy Density as the Source of Information about Clusters
This research utilizes the potential energy density of a gas to estimate the bond parameters of clusters and equilibrium constants for the cluster fractions [5] . We define the potential energy of a gas U(T, P) as the difference between the Internal energy E(T, P) of a real gas and the Internal energy E(T, 0) of an ideal gas at the same temperature. The defined so potential energy reflects all changes of the real gas internal energy with pressure. To apply the mass action law to the potential energy we use its positive density: W(T, P) = −DU(T, P), Figure 5. The series expansion coefficients Wn(T) reflect the contributions of n-particle complexes in the W(T, P). Among these complexes dominate the n-particle clusters, but may be also the n-particle elastic collisions of monomers or elastic collisions of monomers with smaller clusters. For this reason we have to separate from the Wn(T) coefficients the contributions of physical n-particle clusters and contributions of virtual clusters caused by elastic collisions of monomers with smaller clusters and with each other.
From the Figure 5 it’s clear that it is not easy to expand such nonlinear function in a series. Instead, we expand in series by powers of Dm the W2+(T, P) function at a constant T, Figure 6:
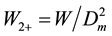 (5)
(5)
The sign “+” means that we deal with a function, but not with the second order coefficient:
 (6)
(6)
At small densities it is possible to find the first three coefficients for dimers: W2, trimers: W3, and tetramers: W4. The errors in the Wn values estimation grow with the order of the expansion term.
3.3. Estimation of the Clusters’ Bond Energies
In this research the zones of temperature, where the Wn coefficients obey to the Boltzmann law, have been discovered for many pure gases. In these zones it got possible to estimate the cluster bond energy En, as the tangent
Figure 5. The potential energy density of the Water vapor at T = 610 K.
Figure 6. The potential energy density of the Water vapor at T = 610 K divided by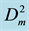 .
.
of slope for the ln(Wn) dependence on 1/T. The estimated so En are measured in K. An example of this procedure is presented at the Figure 7, where the graphs for ln(Wn) versus 1000/T are depicted for the Methanol vapor in the range of temperatures between 200 and 250 K.
A good linearity of graphs shows that both dimer and tetramer fractions obey to the Boltzmann law. Over T = 240 K the graph for tetramers at the Figure 7 becomes unstable. This instability is caused by a small value for maximal density of isochoric data to be processed, equal to 60 µmol/l. To improve stability of the graph for ln(W4) at growing temperature we take initial data for larger densities. Nevertheless, the Figure 7 clearly shows that the tetramer to dimer bond energy ratio is large: E4/E2 = 5.58.
It should be noted that in polar gases, such as methanol or water vapors, the clusters’ bond energies exceed the temperature by one or more orders of magnitude. It gives a hope that the photo dissociation of these clusters may be seen in their spectral characteristics. The spectral lines of cluster fractions should be separated from the molecular spectra by their intensity dependence on the density of a gas.
An extra low density of the Water vapor in atmosphere may require optical path crossing whole atmosphere for spectral determination of Water clusters. For these measurements it is desirable to place a part of scientific apparatuses in space or on standing far apart mountains. The Figure 8 permits to estimate the tetramers’ bond energies in the Water vapor. Near T = 370 K there is a change of bond energies from E4l = 15,380 K at low temperatures to E4h = 4960 K at high temperatures. The transition zone takes around 20 K.
3.4. Estimation of the Dimers’ Bond Energy via Heat Capacity
The described in section 3.3 method of the cluster bond energy estimation seems not to be straightforward enough. For the pair bond energy E2 in dimers the author has developed a direct method of E2 determination from isochoric data for Internal energy E(T, D) and Constant volume heat capacity Cv(T, D):
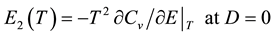 (7)
(7)
Figure 7. Estimation of bond energies En for dimers (red line) and tetramers (blue line) in the methanol vapor at T between 200 and 250 K.
Figure 8. Estimation of bond energies for tetramers in the Water vapor via ln(W4) vs 1000/T dependence (red line). The low and high T trends are shown by thin black lines.
This expression gives the same results for E2(T) as the method, described in the Section 3.3. In this method it is possible to avoid the utilization of the Monomer fraction density Dm because at a near zero density the total density D and Dm do not differ. To calculate the zero density partial derivative ∂Cv/∂E|T it is possible to use also the isobaric data. The Figure 9 shows the temperature dependence of the pair bond energy for dimers in the Water vapor.
For Water vapor clusters the tetramer to dimer bond energy ratio at low temperatures is near 9 that tell about enforcement of bonds in the tetramer structure. In the closed ring structure of a tetramer with 4 bonds this enforcement may be of a factor two! It got impossible to construct a reasonable 3D tetramer structure with larger number of bonds.
3.5. Correction of Dimers’ Data for Monomer-Monomer Elastic Collisions
To come to a flat behavior of E2(T) at high temperatures it was needed to take into account the temperature dependence of monomers elastic collisions’ contribution to potential energy of pair molecular complexes. The flat behavior of E2(T) at high temperatures is a criterion for correctness of a model selected to describe the monomer-monomer elastic collisions’ contribution to potential energy of a gas. For the Water vapor the linear temperature dependence of the monomer-monomer contribution to density dependence of Internal energy has a form:
It leads to a flat E2(T) behavior at high temperatures with a = 0.067 J∙l/(mol2∙K).
4. The Results of the Clusters’ Characteristics Estimation in Polar Gases
4.1. Estimation of the Cluster Fraction Equilibrium Constants
On dividing the Wn values by the bond energy REn, measured in Joule/mole, we receive the cluster fraction equilibrium constant Cun. Index “u” means that these equilibrium constants have been determined basing on the potential energy data. The equilibrium constant found from spectroscopy may differ from the Cun because of its possible sensitivity to the isomer configuration of the n-particle clusters. For the Methanol vapors dimer fraction the equilibrium constant Cu2 (T) is shown at the Figure 10.
Unlike the second virial coefficient [3] , the equilibrium constant for dimers does not change its sign and obey to the Boltzmann law. The Cu4 values for tetramer fraction in the Methanol vapors are shown at the Figure 11.
4.2. Estimation of the Attraction Zone Volumes in Clusters
If we divide the Cu2 by exp(E2/T), we find the effective attraction zone volume V2 for a particle bound with other particle in a dimer. For the Methanol dimers V2 = 0.82 ml/mol in the range of temperatures 200 - 300 K. A small value of V2 for Methanol, as compared to Noble gases [12] , tells about a strong orientation of bonds in dimers, limiting the attraction zone volume in polar gases.
Figure 9. The pair bond energy E2(T) for dimers in the Water vapor, found via constant volume heat capacity.
Figure 10. The equilibrium constant Cu2(T) for the dimer fraction in the methanol vapors.
Figure 11. The equilibrium constant Cu4(T) for the methanol vapors tetramer fraction.
Figure 12 shows the V2(T) values in a wide range of temperatures. It should be noted that near the triple point the V2 values are 7.7 times smaller than at high T. So, a small high T attraction zone volume, as compared to Noble gases, becomes much smaller near the triple point. Therefore, Hydrogen bonds in Water vapor dimers, being strongly oriented at elevated temperatures, become even much more oriented near the triple point.
For tetramers the dimension of Cu4 is (l/mol)3. The same dimension has the tetramers’ attraction zone volume: V4 = Cu4/exp(E4/T). For methanol vapor at T between 200 and 230 K V4 = 3.6 ´ 10−17 (l/mol)3. We can estimate an average attraction zone volume for every Methanol molecule in a tetramer as V1-4 = 
4.3. Soft Structural Transition in Cluster Fractions
The Figure 8 and Figure 9 show that at high temperatures the E2 and E4 values are much lower than near the triple point. It means that at low temperatures intermolecular bonds are much more oriented. The smooth fall of the En(T) dependence was called by the author as the Soft Structural Transition in clusters [11] - [13] . It is the transition from a solid-like cluster structure at low T to the liquid-like structure at elevated temperatures. The freezing of Water cluster fractions starts at higher temperatures than the Water droplet freezing and the number of freezed clusters grows smoothly with lowering the temperature. Unlike the abrupt ice-to-liquid first order phase transition, the melting of clusters takes a wide range of temperatures. The width of the transition zone ∆T is inversely proportional to the difference ∆En between low temperature and high temperature cluster bond energies:
The Figure 8 and Figure 9 show that the larger is the number of particles in a cluster, the narrower is the soft transition zone. For macroscopic droplets we come to an abrupt transition and to precisely determined dew point. For dimers in the Water vapor the central temperature of the Soft transition Tstr = 400 K, ∆E2 = 660 K. So, we come to ∆T = 242 K. The width of the Soft transition zone at the Figure 8 is almost the same.
4.4. New Types of Bonds in the Methanol or Water Low Temperature Tetramers
A small value of the V1-4 to V2 ratio tells that bonds in the Methanol or Water low temperature tetramers are much more oriented than Hydrogen bonds in dimers. They may be 1.5 - 2 times stronger than the Hydrogen bonds existing in dimers and for this reason much more oriented. We can suppose an existence of a quite different type of bonding in the tetramers, rather than bonding in dimers. These bonds may be of a weak chemical bond nature and the tetramers may have a flat closed ring structure, Figure 13, which seems to be much more natural than the 3D tetrahedral structure.
A similar flat ring structure may be attributed to tetramers in the methanol vapors. These tetramers cannot be three dimensional because of asymmetry of their molecules. But at only four bonds in the flat ring structure every bond should be much more energetic than the pair interaction hydrogen bond in dimers.
5. Conclusions
Clusters, being an intermediate form between molecules and condensed matter, influence processes of condensation and their role in nature and technology is significant;
Modern electronic thermophysical databases are sources of knowledge about hidden properties of clusters; to find these properties is a challenge for researchers;
Monomer fraction density based computerized analysis of precise thermophysical data reveals bond parameters of clusters and their equilibrium constants;
The bond parameters for dimers can be found also from the constant volume heat capacity and internal energy data;
Figure 12. The attraction zone volume for molecules in dimers of Water vapor.
Figure 13. A supposed closed ring tetramer structure in the Water vapor at temperatures near the triple point with weak chemical bonds (yellow arrows), which bond energy is 2 times larger than the hydrogen bond energy in dimers. Blue circles―oxy- gen atoms, red circles―hydrogen atoms.
For analyzing series expansion coefficients we should separate contributions of real physical clusters from virtual contributions of monomers colliding with smaller clusters;
The parallel between clusters and macroscopic objects, such as droplets of Water and snowflakes, is very educative;
The discovered clusters’ bond energies temperature dependences reveal the soft structural transition between freezed and liquid-like cluster structures;
Giant bond energies in low temperature water and methanol tetramers may be caused by weak chemical forces.
Acknowledgements
The author thanks Dr. Ilia Brondz for his valuable advice to pay attention to solubility of condensed substances in supercritical fluids that finally led to the discovery of the clusters’ solvation power.
The author would also like to show his gratitude to Dr. Bernard Guy for a warm meeting the Monomer Fraction Density idea in 2007 and advising to consider the nucleation problem.
Cite this paper
BorisSedunov, (2015) Clusters—The Seeds of Droplets and Snowflakes. Voice of the Publisher,01,66-76. doi: 10.4236/vp.2015.13009
References
- 1. Sedunov, B. (2014) The Physics of Clusters in Real Gases. ATINER’S Conference Paper Series, No: PHY2014-1280.
http://www.atiner.gr/papers/PHY2014-1280.pdf - 2. Sedunov, B. (2013) Nanosized Objects in Equilibrium Supercritical Fluids, Proceedings of Joint European days on Equilibrium between Phases, Nancy, March 2013, Article ID: 01062.
- 3. Feynman, R. (1972) Statistical Mechanics; A Set of Lectures. W.A. Benjamin, Inc., Massachusetts.
- 4. Landau, L.D. and Lifshitz, E.M. (1980) Statistical Physics. Pergamon Press, London.
- 5. Sedunov, B. (2013) Thermal Analysis of Thermophysical Data for Equilibrium Pure Fluids. Journal of Modern Physics, 4, 8-15.
http://dx.doi.org/10.4236/jmp.2013.47a2002 - 6. Webbook.NIST (2011) Thermophysical Properties of Fluid Systems.
http://webbook.nist.gov/chemistry/fluid/ - 7. NIST TRC Official Site. NIST Thermodynamics Research Center.
http://trc.nist.gov/ - 8. Kaplan, I.G. (2006) Intermolecular Interactions: Physical Picture, Computational Methods and Model Potentials. Wiley, New York.
http://dx.doi.org/10.1002/047086334X - 9. Aster, R.C., Borchers, B. and Thurber, C. (2012) Parameter Estimation and Inverse Problems. 2nd Edition, Elsevier, Amsterdam.
- 10. Sedunov, B. (2008) Monomer Fraction in Real Gases. International Journal of Thermodynamics, 11, 1-9.
- 11. Sedunov, B. (2012) Equilibrium Molecular Interactions in Pure Gases. Journal of Thermodynamics, 2012, Article ID: 859047.
http://dx.doi.org/10.1155/2012/859047 - 12. Sedunov, B. (2013) Equilibrium Thermal Physics of Noble Gases. Journal of Modern Physics, 4, 8-14.
http://dx.doi.org/10.4236/jmp.2013.412b002 - 13. Sedunov, B. (2013) Equilibrium Structure of Dense Gases. Proceedings of Joint European Days on Equilibrium between Phases, Nancy, March 2013, Article ID: 01002.
http://dx.doi.org/10.1051/matecconf/20130301002 - 14. Sedunov, B. (2012) The Analysis of the Equilibrium Cluster Structure in Supercritical Carbon Dioxide. American Journal of Analytical Chemistry, 3, 899-904.
http://dx.doi.org/10.4236/ajac.2012.312A119 - 15. Sedunov, B. (2011) Structural Transition in Supercritical Fluids. Journal of Thermodynamics, 2011, Article ID: 194353.
http://dx.doi.org/10.1155/2011/194353 - 16. Sedunov, B. (2013) The Equilibrium Thermal Physics of Supercritical Fluids. International Journal of Analytical Mass Spectrometry and Chromatography, 1, 103-108.
http://dx.doi.org/10.4236/ijamsc.2013.12013 - 17. Ford, I.J. (2004) Statistical Mechanics of Nucleation: A Review. Proceedings of the Institution of Mechanical Engineers, Journal of Mechanical Engineering Science, 218, 883-889.
http://dx.doi.org/10.1243/0954406041474183 - 18. Sedunov, B. (2015) The Molecular Physics of Chain Clusters, Abstract Book. ATINER’S 3-rd Annual International Conference on Chemistry & Physics, Athens, 20-23 July 2015.
- 19. Koudryavtsev, A.B., Jameson, R.F. and Linert, W. (2001) The Law of Mass Action. Springer-Verlag, Berlin.
http://dx.doi.org/10.1007/978-3-642-56770-4
















