Received 6 February 2015; accepted 14 March 2015; published 17 March 2015

ABSTRACT

This study examines whether more analyst coverage mitigates the informational risk borne by small investors. Using the investment-price sensitivity as a proxy for stock price informativeness, we find evidence that analysts do not specialize in the production of firm-specific information and substitute for other corporate governance mechanisms. Our results suggest that analysts are outsiders who have less access to firm-level information. The main findings are robust to many aspects of our methodology.

Keywords:

Analyst Coverage, Information Asymmetry, Market Efficiency, Investment-Price Sensitivity

1. Introduction

This paper investigates whether more analyst coverage increases stock price informativeness. We define price informativeness by the association between investment expenditures and stock prices. We argue that stock prices may predict investment because they reflect firm’s fundamentals and convey to managers useful information. Our analysis is motivated by the ongoing debate on the role played by financial analysts. Theoretically, security analysts play two important roles in capital markets. First, analysts gather and disseminate firm-specific information. This informational role can help mitigate information asymmetries between market participants and affect firm’s valuation [1] [2] . Second, analysts can also monitor the management by scrutinizing financial statements and raising questions when they interact with firms’ managers. This monitoring role may reduce managers’ incentives to manipulate accounting numbers [3] [4] .

Despite the potentially useful role of security analysts, the recent financial crisis (2007) has severely shaken investors’ confidence in analysts’ activities. It showed that the dissemination of firm-specific information was inadequate and the quality of research by analysts was questionable. In the literature, some authors argue that analysts improve the efficiency of capital markets by reducing information asymmetries [5] - [7] . Others suggest that investment banking business and trading commissions are the main motives for analysts. One implication of the second view is that analysts will refrain from disclosing negative information that may jeopardize potential investment banking activities, relations with the management, and profitable trading commissions [8] [9] .

Our main contribution is to propose an intuitive methodology that is applied for the first time to international capital markets (21 developed and 23 emerging markets). To our best knowledge, the research design we rely on has been proposed only for US markets. Hence, our empirical findings are shown for the first time in the literature. They will help better understand the impact of analyst activities in non US markets prior to the financial crisis.

Using the investment-price sensitivity as a proxy for the precision of information conveyed by stock prices, we investigate its relation with analyst following. We argue that if analysts enhance the precision of firm-spe- cific information that is reflected in stock prices, we should observe a positive association between analyst coverage and investment to price sensitivity. We find that greater analyst coverage decreases the investment sensitivity to stock prices. Contrary to the conventional wisdom, our findings show that analysts are not a substitute for effective corporate governance mechanisms and do not improve stock price informativeness.

This study is organized as follows: Section 2 reviews previous research on the role of security analysts and describes the empirical methodology. Section 3 provides descriptive statistics and presents the main findings, which are followed by concluding remarks in Section 4.

2. Previous Research Work and Empirical Methodology

2.1. Analyst Activity and Stock Price Informativeness

Many papers examine how analysts’ activities influence firms’ information environment. In 2000, Hong et al. [10] show that private information is reflected in stock prices more slowly for firms with low analyst coverage. Barth and Hutton (2000) [11] results suggest that firms with high analyst coverage incorporate more rapidly information on accruals and cash flow. Furthermore, Frankel and Li [12] in 2004 document negative associations between analyst coverage and insiders trading profits (a proxy for information asymmetry). As for Ayers and Freeman [13] , they show that stock prices incorporate future earnings earlier for firms with high analyst coverage. On the other hand, Piotroski and Roulstone [14] provide evidence suggesting that analyst coverage decreases the amount of firm-specific information in stock prices. Similarly, Chan and Hameed [15] show that analysts generate mainly market-wide information instead of firm-specific information. In 2013, Charest et al. [16] also show that analysts’ activities do not contribute to impound more future earnings information into current stock prices. In the US, Chen et al. [17] find negative relations between analyst coverage and investment- price sensitivity, suggesting that information produced by analysts is not new to firm’s managers.

2.2. Price Informativeness Estimation

In this study, we use the relationship between capital expenditures and stock prices as a proxy for stock price informativeness. Several theories have been proposed to explain why stock prices may predict firm’s investment [18] . The traditional explanation is that firms respond to information about investments opportunities that is reflected in market prices [19] . Such theory assumes that stock prices reflect firm’s fundamentals and respond to changes in the marginal product of capital (efficient and rational capital markets). In fact, when the quality of investment opportunities improves (deteriorates), stock prices should increase (decrease) to reflect positive (negative) NPVs of such opportunities. Subsequently, investment and stock prices should be positively correlated. Based on this theory, if analysts’ activities allow stock prices to reflect NPVs of investment opportunities, more analyst coverage should give rise to a positive association between stock prices and subsequent investment.

Another theory (managerial learning hypothesis) says that stock prices predict investment because they convey to managers information useful in making investment decisions [18] . The advocates of this approach [20] - [22] argue that managers can extract valuable information from their stock prices and use this information when making their investment decisions. According to Chen el al. (p. 620) [17] , “the idea behind the theory is that stock prices aggregate information from many different participants who do not have channels for communication with the firm outside the trading process. Thus, stock prices may contain some information that managers do not have. This information, in turn, can guide managers in making corporate decisions, such as the decision on corporate investments”. Hence, the managerial learning hypothesis predicts a positive relation between investment and stock prices. As suggested by Chen et al. [17] , an important factor contributing to investment- price sensitivity is that managers incorporate what they learn from the private information in prices in their investment decisions. We argue that when managers already know the information produced by analysts or consider such information as irrelevant to making investment decisions, they will not adjust their investments to any new information produced by these markets participants. Theoretically, such information should impact stock prices but not firm’s investment, and this should result in a lower sensitivity of investment to prices [17] . In addition, when managers know more than the public and security analysts, they are expected to rely less strongly on market prices in their investment decisions, and this should also result in lower investment-price sensitivity. Following these arguments, if analysts increase managers’ ability to identify new information relevant to making investment decisions, we should expect firms followed by a large number of analysts to exhibit high investment-price sensitivity. This hypothesis assumes that analysts collect and disseminate information that managers do not have. For instance, analysts can have relevant data about the demand for firm’s products and the competition with other firms, where managers are expected to have less information advantage [17] . Further, security analysts can also teach managers something new about the future state of the economy and so convey information useful in making investment decisions [18] . However, it is also possible that a large portion of the information known by analysts may come from managers. Hence, analyst information should move prices but not investment expenditures because managers will not adjust their investments as they already know the information produced by analysts. We assume that when managers know more than security analysts, we should expect lower sensitivity of investment to prices. On top of that, as argued by Chen et al. (p. 638) [17] : “the presence of analysts may attract more noise trading to the stock. This reduces the content of private information in the stock price and thus decreases the sensitivity of investment to price even further”.

While high investment-price sensitivity is consistent with informative stock prices, it also admits another interpretation. In fact, a third theory (mispricing hypothesis) suggests that corporate investment is sensitive to non- fundamental movements in stock prices [23] . For instance, when it stock price is irrationally low, a firm that needs equity to fund its projects (firm with no sufficient borrowing capacity and internal cash-flows) will be less likely to proceed if it has to issue undervalued shares [23] . On the other hand, when prices are irrationally high, “equity dependent” firms will invest in marginal projects. Normally, these projects would have a negative NPV at a rational pricing. Hence, investment can be particularly sensitive to stock prices in irrational markets. Based on the mispricing theory, if analysts mitigate markets imperfections, firms that are followed by a large number of analysts should exhibit low investment-price sensitivity.

In order to provide robust tests that help separate the traditional and managerial learning theories from the mispricing theory, we propose to isolate the nonfundamental component of stock prices in our tests (underpricing or overpricing). As suggested by Baker et al. (p. 972) [23] : “this is a difficult task, but we try to tackle it by using future realized stock returns-specifically, returns over the three years subsequent to the year in which we measure investment. The idea is that future realized stock returns are a noisy estimate of the future returns expected by managers, which in turn include their views about over- or undervaluation”. Following Baker et al. [23] and Chen et al. [17] , we also use future stock returns as a proxy for mispricing. In fact, when stock prices are irrationally low, equity dependant firms will invest less at (t = 0) while their future returns (t + 3) should be higher knowing that underpriced stocks have higher expected returns going forward, as mispricing is corrected. In the same line of reasoning when stock prices are irrationally high (overpricing), we should expect low future returns (t + 3) as mispricing is corrected and high investment at (t = 0). Hence, the mispricing theory implies that the investment-future returns sensitivity should be negative on average [23] . Our empirical findings do not confirm this prediction indicating that mispricing theory plays a limited role in our analysis. We argue that adding future returns in our main equation is particularly useful in ruling out the mispricing theory as an alternative explanation. We also propose a different approach to control for potential market frictions. Following Baker et al. [23] and Fazzari et al. [24] , we consider equity dependent firms to be small, to have high leverage and low dividend payout ratios. We then rank our sample according to these proxies and examine whether firms that are classified as equity dependent (firms that are more likely to time investment) impact our main results. Again, we didn’t find any support for this prediction.

To implement our empirical tests, we run the following regression:

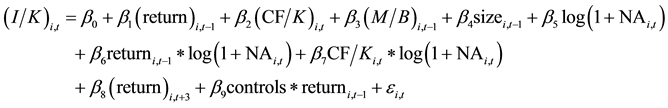(1)

where I_i,t represents investment in plant and equipment for firm i during period t; K denotes the beginning-of- period value of total assets. Our market value variable is stock return in year (t − 1) rather than Q (the ratio of firm’s market value to replacement cost). According to Morck et al. [18] , it is preferable to use returns if we are interested in allowing the maximum scope for the stock market to predict investment. We also prefer stock re- turn because Q is measured with error. It is worth mentioning that our main findings remain unchanged when we use Q instead of stock return. We measure analyst coverage as the logarithm of the number of analysts (NA) that issued one-year-ahead earnings forecasts for firm i during year t. Following Fazzari et al. [24] , we add firm’s cash flow (CF) both separately and in interaction with analyst coverage to control for the well-documented effect of cash flow on investment [24] [25] . Firm’s internal capital (CF) may impact investment because of a fi- nancing hierarchy (Pecking Order Theory), in which internal funding have a cost advantage over external fund- ing [24] . CF is the sum of income before extraordinary items and depreciation net of cash dividends. M/B de- notes the market to book ratio, and size denotes the natural logarithm of firm size. The market to book ratio is a proxy for investment opportunities and growth, while size variable controls for potential market imperfections related to firm size. We also include firm’s future returns (t + 3) to control for managers timing of investment.

Our main interest in Equation (1) centers on β₆, the coefficient of the interaction term (return_i,t−1*log(1 + NA_i,t)) that proxies for the impact of analyst coverage on the relation between investment spending and stock prices. Knowing that high investment-price sensitivity indicates that managers respond to information (private and public) about investment opportunities that is reflected in market price, a positive β₆ means that high analyst coverage increases the precision of information conveyed by stock prices.

3. Data and Empirical Results

The sample construction starts with non US firms originating from 44 countries over the period 1990-2006. As suggested earlier, our purpose is to examine the role played by financial analysts outside the US and during the years before the financial crisis. For each firm, we collect its capital expenditures, stock returns, cash flows, total assets, and a variety of control variables from Worldscope. To be consistent with the literature, we exclude financial firms from our sample. Our main country control variables are given in Table A1. To mitigate the influence of extreme values, regression results are robust to outliers (variables are winsorized at 1% in each tail). We obtain analyst coverage data from the Institutional Brokers’ Estimate System (I/B/E/S). When I/B/E/S does not report an analyst forecast for firm i in year t, we assume that the number of analysts following the firm is zero as suggested by Piotroski and Roulstone [14] . Therefore, our main analysis includes firms with no earnings forecasts. In our robustness checks, we care to exclude such firms.

Table 1 provides descriptive statistics of the main variables used in the study. We present the mean, median, 5^th percentile, 95^th percentile, standard deviation and the number of observations. Given the large proportion of firms with zero analyst coverage, we perform our tests both with and without these firms. A potential concern is that our findings can be influenced by such observations. In fact, as suggested by Chan and Hameed [15] , the absence of firm’s earnings forecasts could mean that there is no analyst coverage or that the data for the firm were not captured by I/B/E/S. The average number of analysts (NA) covering our sample is 1.899 (median of 0). On the other hand, when we drop observations with zero analyst coverage, the average number (NAbis) becomes 5.721 (median of 3). Furthermore, to account for differences in the role played by analysts across countries because of differences in institutions, we also propose to add to our main framework a variety of institutional variables linked to legal and political environment (for more details, see Table 2).

Table 3 summarizes the results from estimates of Equation (1). Column 1, 2, 3 and 4 present coefficients from regressions using observations with zero analyst coverage, while in column 5, 6, 7 and 8 we repeat the same analysis without observations with zero analyst coverage. Column 1 and 5 estimate Equation (1) without using firm’s cash-flow, future return, and countries control variables. Column 2, 3, 4, 6, 7 and 8 include additional controls variables (firm and country level variables). For instance, in Column 3 and 7, we add firm’s

This table presents descriptive statistics for variables used in our analysis. We use a large sample of firms originating from 21 developed markets and 23 emerging markets over the period 1990-2006. For each variable, we provide the mean, median, 5th percentile, 95th percentile, standard deviation and the number of observations. All variables are defined in Table 2.

Investment spending divided by total assets (I/K) is the dependent variable. Return is the fiscal-year-end adjusted share price, plus the adjusted dividends, all divided by the adjusted price at the end of the previous fiscal year. Other explanatory variables are defined in Table 2. We estimate all models using Ordinary Least Square (OLS) regressions with country, year, and industry fixed effects. Country, year, and industry dummies coefficients are not reported for parsimony. In model 1, we estimate equation 1 without firm’s cash-flow, future return and other control variables. In model 2, we include firm’s cash flow. In model 3, we include firm’s cash flow and future returns. In model 4, we add firm’s cash flow, two country-level variables (DRI and GDP), and a dummy variable (CL) that is equal to one if the firm is cross-listed on a US exchange, and zero otherwise. The first set of columns (1-4) present coefficients from estimations using observations with zero analyst coverage. In the remaining models (5-8), we drop observations with zero analyst coverage from the analysis. Standard errors are adjusted for both heteroskedasticity and clustering at the firm level. p-values for two-tailed tests are in parentheses. One, two or three asterisks denote significance at the 10%, 5% and 1% levels, respectively.

cash-flow and future return. In all columns, the coefficients are obtained from OLS estimations with country, industry, and year fixed effects. In fact, we include into Equation (1) a host of dummy variables that capture systematic differences in investment policies across countries (country dummies), industries (2 digit SIC codes dummies), and time (year dummies). In addition, standard errors are adjusted for heteroskedasticity and within- firm clustering as defined in Petersen [26] .

The primary findings suggest that investment is positively correlated with stock prices, supporting the observations in the literature. For instance, in column 1, the coefficient on return_i,t−1 is 0.0005 with a p-value of 0.075. As suggested earlier, we focus more on the coefficient for (return_i,t−1*log(1 + NA_i,t)). In all specifications, this coefficient is negative and significant at 1% level (−0.0063 with a p-value of 0.001 in the case of specification 1). This suggests that, on average, the investment-price sensitivity is lower for firms with high analyst coverage. The findings documented above are consistent with Chen et al. [17] who also show negative associations between analyst coverage and investment-price sensitivity in US markets. Hence, the information produced by analysts and impounded in stock prices is not new to managers. Another explanation of our results is that analysts may attract more noise to stock prices, which will lower the content of private information in stock prices and ultimately reduce the investment-price sensitivity [17] . As for the control variables, cash flow coefficients are positive and significant (at 1% level), confirming the well documented association between cash flow and investment. More important, future return (t + 3) coefficients are not significant, which indicates that the market mispricing theory is not an issue in our study. We also control for the economic development of the country (GDP), legal factors (DRI), and US exchange cross-listings by non US firms (direct listing and ADRs II/III). Arguably, US cross-listings could have a positive or a negative impact on the investment-price sensitivity [27] . Therefore, it is possible that log(1 + NA_i,t) captures the same effects as US cross-listings (CL). Column 4 and 8 put analyst coverage and US cross-listings together. The results indicate that coefficients for (return_i,t−1*log(1 + NA_i,t)) remain negatively significant. Lastly, we control for a variety of political factors (see Table A1 and Table 2 for more details). Adding press freedom, political rights, and corruption (results not tabulated) does not alter our primary findings.

We also check the robustness of our primary results in several ways. First, we re-estimate Equation (1) using firm-fixed effects instead of country and industry fixed effects (see Table 4 for more details). The purpose is to control for unobserved time-invariant firm characteristics. Second, we control for random country effects (see models 7-12 in Table 4). When we capture time-invariant heterogeneity (firm-fixed effects), our coefficient of interest (β₆) becomes non significant, suggesting that investment-price sensitivity is not related to the level of analyst coverage. In other words, high analyst following has no effect on price informativeness. These additional results still suggest that the information produced by analysts and reflected in stock prices is not new to managers. On the other hand, they do not indicate that a high presence of analysts reduces the content of private information in stock prices by increasing noise.

Third, we also consider the fact that analysts’ decision to cover a firm is endogenous. For instance, analysts could self-select the firms they follow according to a variety of firms’ characteristics. Hence, it is possible that some variables not included as controls may simultaneously affect the decision to cover a firm and firm’s investment decision. To mitigate self-selection concerns, we use the two-stage Heckman procedure. In the first stage, we model the choice of covering a firm through a probit model. Following prior studies [14] [15] , we consider that analyst activities are affected by the following variables: firm size, return volatility (RV), earnings volatility (EV), trading volume (TV) and firm’s ownership (O).

Then, we propose the following model (coverage decision equation):

This table presents the results of Equation (1) with two additional estimation techniques. The first set of columns (1-6) present coefficients from an estimation of the model using firm and year fixed effects. In the remaining columns (7-12), we estimate variants of equation 1 by including country random effects. We report p-values (in brackets) based on heteroskedasticity corrected standard errors that are clustered at the firm level. One, two or three asterisks denote significance at the 10%, 5% and 1% levels, respectively.

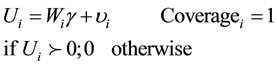(2)

where U_i is an unobserved latent variable (utility of analyst i to cover a firm) and W_i is a set of variables that affect the decision of analysts to cover a firm. We don’t observe U_i. All we observe is a dichotomous variable Coverage_i with the value of one if the firm has analysts that follow its activities (U_i > 0) and 0 otherwise. Table 5

This table reports coefficients and test statistics of the Heckman (1979) two-stage procedure. In the first set of columns, we report the results of the probit estimation (first-stage) where the dependent variable is a dummy that is equal to one if the firm is followed by analysts, and zero otherwise. The second set of columns report the OLS estimates of our main equation (second-stage). We also include the Inverse Mills ratio (λ). In our analysis, we use the logarithm of the number of analysts (log(1 + NA)) and observations with zero analyst coverage. Regressions include country, industry, and year fixed effects. p-values for two-tailed tests are in parentheses. One, two or three asterisks denote significance at the 10%, 5% and 1% levels, respectively.

presents the results of the Heckman [28] procedure. Again, the coefficients on the interaction between firm’s return and analyst coverage (second stage estimation) are negative and significant (at 1% level). Hence, our primary findings are robust to self-selection.

In our study, we also estimate the relation between analysts’ activities and investment-price sensitivity separately for “equity dependent” and “equity independent” firms. As suggested earlier, the purpose of this additional test is to examine whether the mispricing theory can be considered as an alternative explanation. In this case, our conclusions should change. The results (not tabulated) indicate that analysts’ impact on price informativeness is the same for both subsamples, which rules out the mispricing theory as an alternative explanation.

4. Conclusions

We have examined the impact of analyst coverage on price informativeness. We find a negative association between analyst coverage and investment-price sensitivity, which suggests that the information produced by analysts is not new to firm’s managers. In other words, analysts do not have an informational advantage over firm’s insiders. This paper sheds some light on the role played by financial analysts before the financial crisis. In fact, our findings suggest that the dissemination of reliable information by analysts was inadequate during this period. This lack of firm-specific information may have affected the efficiency of capital markets around the world and led to the financial crisis.

Our study has its limitations. First, we do not cover the post-crisis period. Future research could investigate whether our findings are still relevant in the post-crisis period. Second, although our results are “robust” to the mispricing theory, it may be interesting to propose other tests that address this important issue. This will offer further validation of the actual findings.

References

Appendix

This table summarizes the data for shareholders’ protection and country political risks. All variables are defined in Table 2.