American Journal of Industrial and Business Management
Vol. 2 No. 1 (2012) , Article ID: 17111 , 6 pages DOI:10.4236/ajibm.2012.21002
Comparison of Analytic Hierarchy Process and Dominance-Based Rough Set Approach as Multi-Criteria Decision Aid Methods for the Selection of Investment Projects
![]()
Université du Québec en Abitibi-Témiscamingue, Rouyn-Noranda, Canada
Email: {*boudreab, *kazimierz.zaras}@uqat.ca
Received September 29th, 2011; revised November 28th, 2011; accepted December 20th, 2011
Keywords: Analytic Hierarchy Process; Dominance-Based Rough Set Approach; Management Decision Support System; Multi-Criteria Analysis
ABSTRACT
This investigation compares two multi-criteria analysis methods, Analytic Hierarchy Process (AHP) and Dominancebased Rough Set Approach (DRSA), applied to the ranking of ten investment projects based on evaluation of the overall risk associated with each. AHP requires decision makers to evaluate the various elements of risk by paired comparison in terms of their impact on the element above them in the hierarchy. Each investment project is then rated in terms of each risk to produce a weighted summation used for ranking purposes. DRSA produces a ranking based on a set of decision rules that are derived from evaluation of a reduced number of reference projects well known to the decision makers. For this purpose, four reference projects were chosen from the ten. The results show that the two methods gave very similar final rankings of the ten projects. The advantage of DRSA is that the projects are evaluated using a reduced number of attributes without explicit knowledge of their impact in the hierarchy, thus eliminating a lengthy and tedious process for the decision makers.
1. Introduction
This study was carried out in the Abitibi-Témiscamingue region, located in the southwest portion of the province of Québec (Canada). Of the 5937 businesses in this region (the fourth largest in the province), 96% are small and medium-sized with less than 50 employees [1]. Since such businesses have fewer opportunities for financing than larger businesses, which can issue shares, bonds or other securities, development agencies have a major role to play in providing support to them, especially for financing. Agencies such as the Community Futures Development Corporation (CFDC), the Business Development Bank of Canada (BDC), Regional Development Centres (CLD), Investment Quebec (IQ) are thus represented in this region. These agencies must evaluate numerous projects in a wide range of fields. However, their aim in all cases remains to evaluate objectively and to select the best projects, generally meaning the least risky. In order to protect the confidentiality of the participants in the present study, the names of the agencies involved are withheld.
1.1. Research Objective
The aim of this study is to propose a tool for increasing the productivity of decision makers responsible for selecting projects worthy of funding by regional development organizations. This selection is based on the estimated probability of the business reimbursing the loan.
To make a judicious selection, the decision maker must consider numerous quantitative as well as qualitative criteria. Multi-criteria analysis methods are therefore suitable for solving this type of decision-making problem [2]. The literature devoted to multi-criteria analysis methodology is vast, especially in the subject area of project selection. Shpak and Zaporojan [2] evaluated several methods. Coffin and Taylor [3] discussed applications of fuzzy logic theory in project selection. Lockett and Stratford [4] and later Regan and Holtzman [5] used 0 - 1 mathematical modeling for the project selection decision and fund allocation problem. Ghasemzadeh et al. [6] introduced a 0 - 1 integer linear model for project portfolio selection and scheduling. Saaty [7], Lee et al. [8] and Dey [9], like many other authors, demonstrated that the analytic hierarchy process (AHP) could be used to solve the project selection problem.
In our study, we used AHP to weight the criteria, after which we applied the multi-criteria scoring model to rank the projects, as done by Yurdakul and Tansel [10], using a feature contained in the Expert Choice software dedicated to AHP. We then addressed the same selection problem using the Dominance-based Rough Set Approach (DRSA).
The two methods differ both in theory and practice in the assessment of decision-maker preferences. The AHP method consists of defining all relevant criteria and then doing paired comparisons to evaluate the impact of each criterion. The judgments must be checked for consistency and revised if necessary. These impact ratings are used to calculate a weighted score for each of the objects (e.g. projects) to establish a ranking. The judgment of the decision maker, solicited at the outset for criteria decomposition and hierarchy, is also involved in the weighting of the criteria. In practice, judgment is seldom perfectly consistent. In performing the paired comparisons, the decision maker may consider criterion A more important than criterion B, criterion B more important than criterion C, but criterion C more important than criterion A. He may thus provide judgments with inconsistent proportions. The AHP method allows imperfect consistency in series of paired comparisons and when the scales used are verbal. According to Saaty [11], when the consistency ratio (see Equation 1) is less than 0.1, consistency is sufficient.
The DRSA method is a learning approach based on examples. We do not need to know the weights associated with the criteria. Reference objects well known to the decision makers are usually available, and these can be ordered in a manner that expresses how the evaluation and selection process is done in the field. However, in processing the information thus provided by the decision maker, certain difficulties may arise, as in the AHP method, because of inconsistency and contradiction among the chosen examples. According to Pawlak [12], the preferred model should neither correct nor ignore these contradictions, but rather consider them in the inductive derivation of decision rules, which may thus be designated as certain or uncertain. In practice, certain decision rules are preferred for ordering the entire set of objects.
1.2. The Multi-Criteria Approach
The multi-criteria approach used here relates to the class of problems that can be represented by the AXE model, in which:
A is a finite set of investment projects ai
for i = 1, 2, …, n;
X is a finite set of criteria Xk for k = 1, 2, …, m; and E is the set of project evaluations Eik with respect to criterion Xk.
Our multi-criteria approach consists of establishing an overall preference among the set of projects, based on performance as evaluated with respect to each criterion.
1.3. Description of Projects
Table 1 provides a description of the ten projects evaluated in the present study. These were selected from the financial organization historical database as representative of low-risk projects (project A) and very risky projects not financed (project F), plus eight other projects chosen randomly.
The projects were renamed A to J to preserve anonymity. The average loan amortization period was 63 months and the amounts loaned averaged $57,000. The number of loans received from the organization ranged from one to seven, for an average of 2.2. A value of 1 thus indicates that this was the first experience of the business with the lender.
2. Analytic Hierarchy Process
The analytic hierarchy process or AHP method combined with the multi-criteria scoring model was the decision tool used to perform our initial evaluation of the overall risk associated with each of the ten projects obtained from the historical database. Developed by Thomas L. Saaty in the 1970s, the AHP method is still evolving [7, 11,13]. It is used around the world for a wide variety of non-structured, complex and multi-attribute management problems, which is the case here.
2.1. The Steps of the AHP Method
In order to put this decision-aid method to proper use,
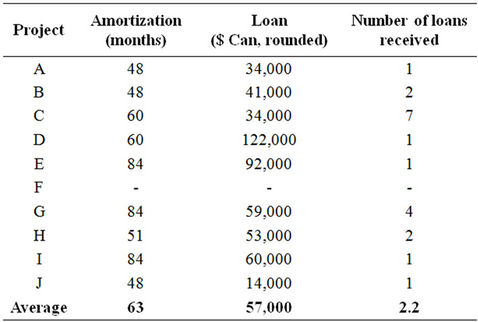
Table 1. The ten projects evaluated in the study.
several steps must be followed in a prescribed order. Below is a description of how we proceeded for each step.
1) Identification of a coherent family of criteria: We began by querying four financial organizations regarding the criteria they used to evaluate overall risk. We made a summary of the criteria thus identified and showed it to representatives of the development agency that participated in this study. From the summary, these representatives chose 24 criteria that they viewed as the most important (see Table 2). We set these in a hierarchical structure with four levels. Level 0 represents the main goal, which is to evaluate the overall risk associated with the project. Level 1 contains attributes representing four broad categories of risk: managerial, financial, technical and business. Level 2 contains attributes representing aspects of each of the risks in level 1, two for managerial, financial and technical and five for business risk. Level 3 contains attributes representing the 24 criteria, which are each aspects of some level-2 attribute.
2) Paired comparison: Horizontal pairings were done within each level of the hierarchy. Each attribute was thus compared to each other attribute connected to the same immediate hierarchical superior. The four participating decision makers (three men, one woman) in the employ of the development agency had an average of 4.5 years of experience in financing and their average age was 35. Each of them carried out the paired comparisons on the nine-point Saaty scale, using Expert Choice software.
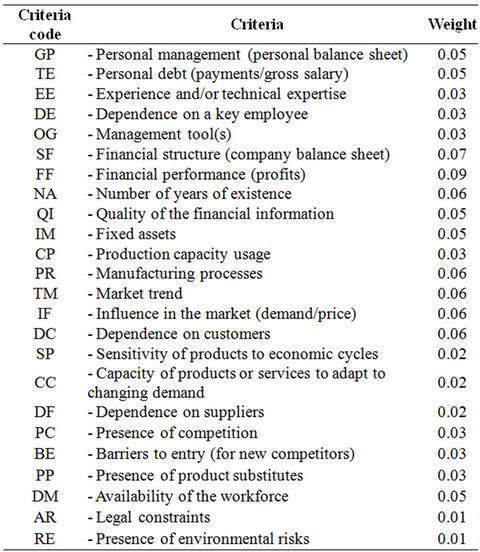
Table 2. The weights of the criteria.
3) Normalization: With the paired comparisons thus obtained from each decision maker, we calculated the geometric mean to obtain the final prioritization of the criteria as suggested by Xu [14]. Normalization was also done using Expert Choice software. This allowed us to determine the weights on each level for each attribute and criterion. For the 24 criteria on level 3, we obtained final weights shown in Table 2.
4) Analysis of consistency: In using AHP, the decision maker should be consistent in his judgment. For example, if the decision maker strongly prefers A to B and B to C, it would be inconsistent for him or her to indicate indifference regarding C and A or preference of C to A. To determine whether or not inconsistency is excessive, we compute the following indexes:
Consistency Index (CI):
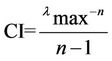 (1)
(1)
and Consistency Ratio (CR) = CI/RI; where λ is the average consistency measured for all projects; RI is the appropriate random index given by Saaty for n, the number of alternatives (projects); If CR < 0.10, the consistency is acceptable. If CR > 0.10, the comparison process should be repeated. In the present study, CR = 0.079.
5) Performance function: For each criterion of the last level, we determined a performance function, which allows us to compute the weighted average score for each project after its evaluation. Here is an example of the performance function used for criterion Xk, personal debt (payments/gross salary):
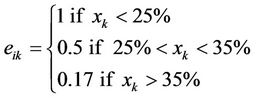 . (2)
. (2)
If the personal debt ratio represents less than 25%, then the performance on this criterion is 1/1. If the ratio is between 25 and 35%, then the performance on this criterion is 0.5/1. If it is superior to 35%, then the performance on this criterion is 0.17/1. To obtain the score for each of the ten projects using the multi-criteria scoring model, we compute: weighted average score for project
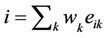 (3)
(3)
where wk is the weight of criterion k obtained from AHP; eik is the evaluated performance of project i based on criterion k.
The purpose of the multi-criteria scoring model is to assign to each project a value from 0 to 1 reflecting its relative performance based on each criterion. Ranking of the projects based on the weighted average score is shown in Table 3.
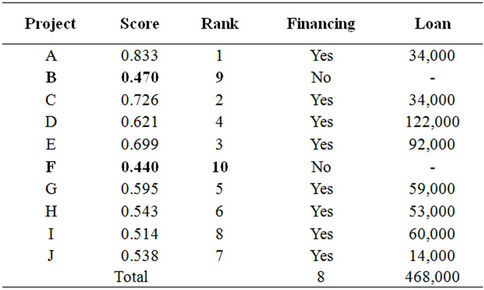
Table 3. Final weights using AHP.
These results are very consistent with the initial judgment of the experts. Project A, judged the least risky, received the highest score (0.833), while project F, judged not worthy of financing, received the lowest score (0.440). In the opinion of these decision makers, no project with a lower score than 0.5 should be financed. On this basis, project B should not have been financed. For the eight projects that were found worthy of financing, a total of $468,000 (Can) was invested.
2.2. Advantages and Drawbacks of the AHP Method
The main advantage for decision makers using AHP is the relative consistency and impartiality of the evaluation obtained for each project. The main drawback is the time required. The paired comparisons take considerable time and all projects need to be evaluated with respect to all criteria (24 in the present case). We spent two to three hours on each project evaluation. For the ten projects, we needed about 25 hours to complete the evaluations.
Based on the results obtained, it can be stated that AHP is useful, but a quicker way of evaluating projects would be appreciated.
3. Rough Set Methods
3.1. Description
The second decision method that we considered is based on the rough set theory proposed by Pawlak [12,15] and developed by Greco et al. [16] and Zaras [17]. The approach of Greco et al. assumes that a principle of dominance is respected and is thus called the dominance-based rough set approach (DRSA). It consists of finding a reduced set of criteria that provides the same quality of classification of the original set of objects as obtained using, in our case, AHP.
In rough set theory, the decision problem is represented as a table, the rows corresponding to objects and the columns to attributes (see Table 4). In our approach,

Table 4. Decision table.
the objects are the pairs of investment projects and we used two types of attributes: conditional and decisional. The agents (experts or decision makers) participating in the decision process make their decisions among the chosen few reference objects. According to Thibault et al. [18] and Kane et al. [19], a subset of four to seven objects is sufficient, so we used four investment projects. This decision in the decision table with respect to the decisional attribute takes one of two values: if project ai is preferred overall to project aj, it is denoted P, otherwise N. In this case, the preferences in the decision tables were supposed to be the same as those obtained using the multi-criteria scoring model.
The remaining attributes will be called conditionals and these will be from our multi-criteria AXE problem (the 24 criteria of the last level in the AHP method). With respect to each conditional attribute, the evaluation of the pairs of alternatives (i.e. investment projects) may take one of three values: one (1) if project ai outranks project aj, zero (0) if it does not and 0.5 if the projects are judged equal.
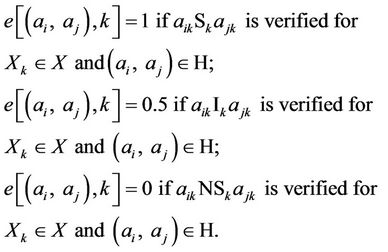 (4)
(4)
Figure 1 shows a portion of the results from the table of the four investment project evaluations with respect to the 24 conditional criteria and one decisional criterion.
3.2. Decision Rules
The calculations were done with computer package 4eMka2 developed by the Intelligent Decision Support Systems (IDSS) laboratory at the Institute of Computing Science, Poznan University of Technology.
The computer package identified many (92) reduced subsets of criteria and decision rules, a few of which are shown below:
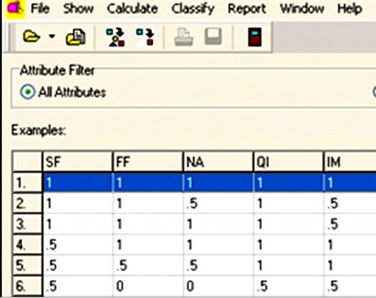
Figure 1. Evaluation of the project with respect to conditional criteria.
Rule 1. (PC 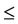 0)
0) 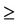 (DEC at greatest N); [5, 83.33%] {7, 8, 9, 10, 11}
(DEC at greatest N); [5, 83.33%] {7, 8, 9, 10, 11}
Rule 2. (BE  0)
0) 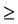 (DEC at greatest N); [4, 66.67%] {7, 8, 11, 12}
(DEC at greatest N); [4, 66.67%] {7, 8, 11, 12}
Rule 3. (PC  1)
1) 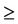 (DEC at least P); [5, 83.33%] {1, 2, 3, 4, 5}
(DEC at least P); [5, 83.33%] {1, 2, 3, 4, 5}
Rule 4. (BE  1)
1)  (DEC at least P); [4, 66.67%] {1, 2, 5, 6}
(DEC at least P); [4, 66.67%] {1, 2, 5, 6}
The rules above are based on the reduced subset of two criteria, namely PC (presence of competition) and BE (barriers to entry for new competitors).
The weight of these criteria as measured using AHP (0.03 for both) was not very high. The Decision-based Rough Set Approach (DRSA) nevertheless led us to decision rules based on them. The rules mean that if project ai outranks aj with respect to at least one of these two criteria, it must be preferred overall to aj.
3.3. Quality of Approximation
The quality of approximation is equal to one and the boundary region is empty, which means that based on the conditional criteria, the preferences are defined in a crisp manner.
Quality of approximation: 1.000000 at greatest N: 1.0000 P-lower approximation: [6] {7, 8, 9, 10, 11, 12}
P-upper approximation: [6] {7, 8, 9, 10, 11, 12}
P-boundary: [0] {}
at least P: 1.0000 P-lower approximation: [6] {1, 2, 3, 4, 5, 6}
P-upper approximation: [6] {1, 2, 3, 4, 5, 6}
P-boundary: [0] {}
Table 5 shows the final ranking of the projects, obtained by verification of the decision rules for the entire set of ten investment projects and by using the Net Flow Score (NFS) known from applications in the PROMETHEE method [20].
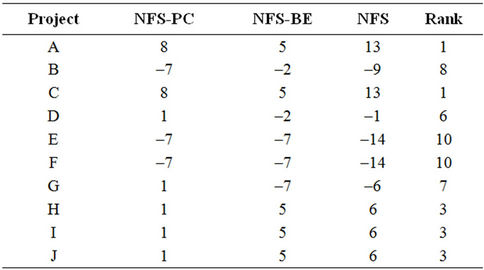
Table 5. Final ranking with DRSA.
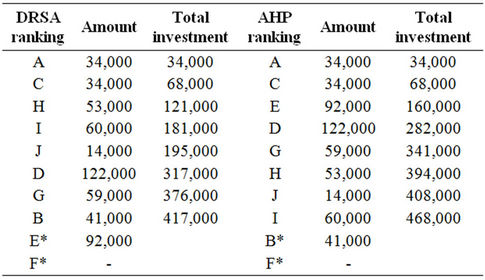
Table 6. Rankings obtained by DRSA and AHP.
4. Results and Comparison of the Two Methods
From a methodological point of view, criteria need to be identified that are suitable for both of the methods. AHP is based on the assessment of weights, which are not needed for DRSA. The multi-criteria scoring model is analytical and consists of calculating the average weighted value for each project in order to identify decision-maker preferences. DRSA is an example-based learning model in which the decision rules are inductively derived. The set of rules expresses the preferences of the decision maker. These rules can be applied to rank a large number of projects. With the AHP method, the time and cost of the assessment of the weights and scores increases signifycantly with the number of criteria and projects.
The rankings obtained by AHP and DRSA are very similar (see Table 6). DRSA ranking is based on only two criteria, while AHP ranking is based on 24 criteria. It can be concluded that the two decision aid methods would yield very similar results from the same investment envelope of $468,000. AHP recommends not financing projects B and F, while DRSA recommends not financeing projects E and F. Using either decision aid method, projects A and C came to the top of the list, while project F was at the bottom.
Based on these results, we suggest that the DRSA method may allow reductions in the cost and time allotted to the project evaluation process. Rather than spending many hours evaluating the 24 criteria used with the AHP tool (a tedious, wearying and hence error-prone process), there is a possibility of evaluating only two criteria and obtaining very similar results.
REFERENCES
- Observatory of the Abitibi-Témiscaminigue, “Number of Establishments and Jobs According to the Size and the MRC, Abitibi-Témiscamingue,” 2011. http://www.observat.qc.ca/statistiques/45/entrepreneuriat
- A. Shpak and D. Zaporojan, “Working Out R & D Programs via Multicriteria Analysis,” Computer Science Journal of Moldova, Vol. 4, No. 2(11), 1996, pp. 239- 259.
- M. A. Coffin and B. W. Taylor, “Multiple Criteria R & D Project Selection and Scheduling Using Fuzzy Logic,” Computer & Operations Research, Vol. 23, No. 3, 1996, pp. 207-221. doi:10.1016/0305-0548(96)81768-0
- G. Lockett and M. Stratford, “Ranking Research Projects, Experiments with Two Methods,” Omega, Vol. 15, No. 5, 1987, pp. 395-400. doi:10.1016/0305-0483(87)90040-5
- P. Regan and S. Holtzman, “R & D Decision Advisor: An Interactive Approach to Normative Decision System Model Construction,” European Journal of Operational Research, Vol. 84, No. 1, 1995, pp. 116-133. doi:10.1016/0377-2217(94)00321-3
- F. Ghasemzadeh, N. P. Archer and P. Iyogun, “A ZeroOne Model for Project Portfolio Selection and Scheduling,” Journal of Operational Research Society, Vol. 50, No. 7, 1999, pp. 745-755.
- T. L. Saaty, “The Analytic Hierarchy Process,” McGrawHill, New York, 1980.
- A. H. I. Lee, H. H. Chen and H. Y. Kang, “Multi-Criteria Decision Making on Strategic Selection of Wind Farms,” Renewable Energy, Vol. 34, No. 1, 2009, pp. 120-126. doi:10.1016/j.renene.2008.04.013
- P. K. Dey, “Integrated Project Evaluation and Selection Using Multiple-Attribute Decision-Making Technique,” International Journal Production Economics, Vol. 103, No. 1, 2006, pp. 90-103. doi:10.1016/j.ijpe.2004.11.018
- M. Yurdakul and Y. Tansel, “AHP Approach in the Credit Evaluation of the Manufacturing Firms in Turkey,” International Journal of Production Economics, Vol. 88, No. 3, 2004, pp. 269-289. doi:10.1016/S0925-5273(03)00189-0
- T. L. Saaty, “Fundamentals of the Analytic Network Process-Multiple Networks with Benefits, Opportunities, Costs and Risks,” Journal of Systems Science and Systems Engineering, Vol. 13, No. 3, 2004, pp. 348-379. doi:10.1007/s11518-006-0171-1
- Z. Pawlak, “Rough Sets,” International Journal of Parallel Programming, Vol. 11, No. 5, 1982, pp. 341-356.
- T. L. Saaty, “Relative Measurement and Its Generalization in Decision Making—Why Pairwise Comparisons Are Central in Mathematics for the Measurement of Intangible Factor, the Analytic Hierarchy/Network Process,” Review of the Royal Spanish Academy of Sciences, Series A, Mathematics, Vol. 102, No. 2, 2008, pp. 251-318. doi:10.1007/BF03191825
- Z. Xu, “On Consistency of the Weighted Geometric Mean Complex Judgement Matrix in AHP,” European Journal of Operational Research, Vol. 126, No. 3, 2000, pp. 683- 687. doi:10.1016/S0377-2217(99)00082-X
- Z. Pawlak, “Rough Sets: Theoretical Aspects of Reasoning about Data,” Kluwer Academic Publishing, Dordrecht, 1991.
- S. Greco, B. Matarazzo and R. Słowiński, “Rough Sets Theory for Multi-Criteria Decision Analysis,” European Journal of Operational Research, Vol. 129, No. 1, 2001, pp. 1-47. doi:10.1016/S0377-2217(00)00167-3
- K. Zaras, “Rough Approximation of a Preference Relation by a Multi-Attribute Dominance for Deterministic, Stochastic and Fuzzy Decision Problems,” European Journal of Operational Research, Vol. 159, No. 1, 2004, pp. 196-206. doi:10.1016/S0377-2217(03)00391-6
- J. Thibault, D. Taylor, C. Yanofsky, R. Lanouette, C. Fonteix and K. Zaras, “Multicriteria Optimization of a High Yield Pulping Process with Rough Sets,” Chemical Engineering Science, Vol. 58, No. 1, 2003, pp. 203-213. doi:10.1016/S0009-2509(02)00470-0
- H. Kane, K. Zaras and M. Nowak, “Using the Dominance-Based Rough Set Approach in Production Planning and Control,” Journal of Global Business Administration, Vol. 1, No. 1, 2009, pp. 23-37.
- J. P. Brans, P. Vincke and B. Mareshal, “How to Select and How to Rank Projects: The PROMETHEE Method,” European Journal of Operational Research, Vol. 24, No. 2, 1986, pp. 228-238. doi:10.1016/0377-2217(86)90044-5
NOTES
*Corresponding authors.

