Received 23 August 2015; accepted 6 November 2015; published 9 November 2015

ABSTRACT

This paper examines optimal control of transmission dynamics of Mycobacterium ulceran (MU) infection. A nonlinear mathematical model for the problem is proposed and analysed qualitatively using the stability theory of the differential equations, optimal control and computer simulation. The basic reproduction number of the reduced model system is obtained by using the next generation operator method. It is found that by using Ruth Hurwitz criteria, the disease free equilibrium point is locally asymptotically stable and using centre manifold theory, the model shows the transcritical (forward) bifurcation. Optimal control is applied to the model seeking to minimize the transmission dynamics of MU infection on human and water-bugs. Pontryagin’s maximum principle is used to characterize the optimal levels of the controls. The results of optimality are solved numerically using MATLAB software and the results show that optimal combination of two controls (environmental and health education for prevention) and (water and environmental purification) minimizes the MU infection in the population.

Keywords:

MU, Optimal Control, Stability, Pontryagin’s Maximum Principle, Reproduction Number

1. Introduction

Mycobacterium ulceran (MU) is a pathogenic, toxin-producing bacterium that is the causative agent of Buruli ulcer (BU), a necrotizing skin infection in humans [1] . Mycobacterium ulceran (MU) is the third most frequent mycobacterial disease in humans, after tuberculosis and leprosy. Although the disease was first reported in Africa in 1897 by Sir Albert Cook, who described large ulcers caused by MU in Uganda, the first definitive description of Mycobacterium ulceran was published in 1948 [2] . Buruli ulcer has been reported mostly in tropical countries in Africa, Central and South Eastern Asia, and to a lesser extent, in America.

The BU disease infects the skin and subcutaneous tissues resulting in indolent ulcers, with lesions appearing mainly in the limbs. The ulcers grow slowly and release a toxin which damages the skin and underlying tissue. The toxin produced by the causative organism is named Mycolatone, a class of polyketides derived from manolides. The toxin destroys large areas of the skin after manifesting itself in the form of painless dermal nodules [3] .

The mode of transmission of MU currently is unclear for many scholars. There are some hypotheses that have been proposed in connection to the mode of transmission of MU. One of the hypotheses says that the microbe is transmitted through the aquatic environment, whereas MU could infect humans who have frequent contact with contaminated water through swimming or through body injuries that facilitate the introduction of the microbe into the skin. Another hypothesis suggested that MU can be transmitted through the bite of aquatic bugs [4] . [4] demonstrated and fitted a mathematical model that estimated the networks of pathogen transmission of MU. The study narrated that MU is transmitted through a web of ecological interactions between potential host carriers in the aquatic environment. [4] studied and developed a mathematical model to analyse transmission of Mycobacterium ulceran. They used the mathematical model which exploits the dynamics of infectious diseases to investigate the epidemiology of BU. From their model equation, it was revealed that the prevalence of BU in humans depends on the biting rate of water-bugs, their mortality rate and arsenic (As) concentration in the environment.

Some studies have exposed various methods of controlling the MU which cause Buruli ulcer (BU). The studies include Mycobacterium bovis basillus Calmetle-Guerin BCG vaccination as prophylaxis against Mycobacterium ulcerans osteomyelitis in Buruli Ulcer Disease for which it recommends BCG vaccination at birth as a control mechanism [5] . Another study was on efficacy of the combination of Rifampin-Streptomycin in preventing growth of Mycobacterium ulcerans in early lesions of Buruli ulcer in humans. The findings of this study indicated that the effectiveness of Rifampicin and Streptomycin in 4 weeks or more, inhibited growth of MU [6] . However, none of the above studies applied the optimal control on controlling the transmission dynamics of MU infection. Therefore in this paper, it intended to apply the optimal control on transmission dynamics of MU infection.

2. Model Formulation

This section investigates the dynamics of Mycobacterium ulceran in a human population as well as that of the vector population. Environmental factors such as arsenic (As) concentration have an influence on the disease prevalent in the population. To understand the transmission dynamics of MU in a population, a mathematical model is developed and analysed. The model discussed describes the dynamics of the two different populations that interact and cause the spread of the disease.

In formulating the model, the following assumptions are taken into consideration:

1) MU infection can arise to the population when there is interaction between human and water bugs.

2) Person to person transmission is excluded.

3) Seasonal variations in the life cycle of the water-bug are negligible.

4) Human population and water-bug populations are homogeneous.

5) Human population is constant.

6) Whenever humans are within the vicinity of the breeding grounds of the water-bugs, they are randomly bitten by the bugs.

The proposed model subdivides the population of interest into two sub populations; human population and vector population. Human population “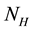” is divided into two groups; Human at risk of been infected by MU “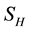” human infected by MU “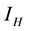”. The vector (water-bug) population “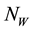” is also divided into two groups; susceptible vector not infected by MU “” and vector infected by MU “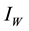”. The model is added to another class known as water contamination “v” containing MU. New infections occur in both populations after interaction between susceptible human and infected vector, susceptible vector and infected human respectively. It has been discussed in several literatures that MU occurs mostly in aquatic environment. In addition, if high levels of As concentration prevail in such environments, the occurrence of MU is enhanced [4] . Arsenic with the concentration rate a enters the aquatic environment and cause contamination to it. The bugs contact with this contaminated water (contain MU) eventually and thereafter become infectious at the rate of. The interaction between susceptible human and infected (vector) water-bugs cause MU infection to human 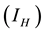at the rate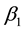. Again infected human 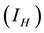can interact with susceptible water-bugs and cause MU to arise to the vectors, which also cause infection to them at the rate of. As it is assumed that human population is constant and no season variation for water-bugs, the rate of recruitments and death rate to both populations are the same. The rate of recruitment and death are 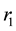for human population and 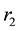for water-bugs population. The aquatic environment can undergo decontamination at the rate of.

Taking into account the above considerations, we have the following schematic flow diagram for the model without control.

The dynamics of the groups described above and as shown in the model flow chart (Figure 1) are described by the system of differential equations given below:

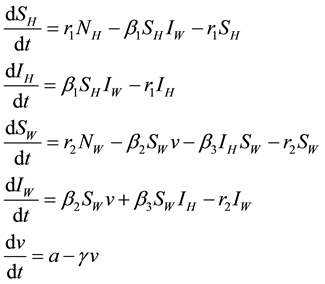(1)

Since human population is constant and water-bugs seasonal variation is neglected, then we can analyse the three classes of infected human, infected water-bugs and water contamination.

(2)

Let,. Then

(3)

Let again,. Then

(4)

We substitute Equation (3) and Equation (4) into equation systems (2) to get

(5)

Let and. Then the system (5) becomes

(6)

3. Model Analysis

The reduced model system of Equation (6) will be analysed qualitatively to understand the transmission dynamics of MU infection in a population. Threshold which governs persistence of the MU infection will be determined.

3.1. Disease Free Equilibrium (DFE)

The disease free equilibrium point of the reduced model system (6) is obtained by setting

Thus we have

(7)

(8)

(9)

Since we are dealing with disease free equilibrium then we set as it is assumed that there is no infection.

Therefore the Disease Free Equilibrium (DFE) denoted by of the reduced model system (6) is given by

(10)

3.2. The Basic Reproduction Number R₀

The basic reproduction number, denoted by is defined as the effective number of secondary cases produced in a completely susceptible population by a typical infective individual [7] . This definition is given for the models that represent spread of infection in a population. It is obtained by taking the largest (dominant) eigenvalue (spectral radius) of

, (11)

where, is the rate of appearance of new infection in compartment i, is the transfer of individuals into the compartment i, is the rate of transfer of individuals out of compartment i and is the disease free equilibrium point. It is assumed that each function is continuously differentiable at least twice with respect to each variable and.

From the equations system (6), it follows that

By linearization approach, the associate matrix at disease free equilibrium is obtained as

. (12)

This is equivalent to

. (13)

The Jacobian matrix of the system (13) at the disease free equilibrium point is

(14)

The transfer of individuals out of the compartment i is given by

.

The Jacobian matrix of at is calculated as

.

This gives

. (15)

with

(16)

Thus

Thus the eigenvalues of are

Then the effective reproduction number which is given by the largest eigenvalue for the reduced model system (6) is given by

.

3.3. Numerical Sensitivity Analysis

In determining how best to reduce human mortality and morbidity due to MU infection, the sensitivity indices of the reproduction number to the parameters in the model was calculated using approach of [6] . These indices tell us how critical each parameter is to disease transmission and prevalence. Sensitivity analysis discovers parameters that have a high impact on. Sensitivity indices allow us to measure the relative change in a state variable when a parameter changes [7] . The sensitivity index of a variable to a parameter is a ratio of the relative change in the variable to the relative change in the parameter. When a variable is a differentiable function of the parameter, the sensitivity index may be alternatively defined using partial derivatives.

Definition 1. The sensitivity index of a variable “p” that depends differentiable on a parameter “q” is defined as:

. (17)

Having an explicit formula for in Equation (17), we derive an analytical expression for the sensitivity of as to each of parameters involved in. For example the sensitivity indices of with respect to and are given by and

respectively. Other indices, , and, are obtained following the same method and tabulated as follows:

Interpretation of Sensitivity Indices

From Table 1, generally it is seen that the parameters when each is increased keeping the other parameters constant, they increase the value of implying that they increase the endemicity of the disease or

they accelerate the transmission of MU in the population as they have positive indices. While the parameters and when each increases while keeping the other parameters constant, they decrease the value of implying that they decrease the endemicity of the disease as they have negative indices.

Specifically, the most sensitive parameter is recruitment/death rate of water-bugs, followed by the rate of MU infection on human due to the interaction of susceptible human with infected water-bugs and the rate of MU infection on water-bugs due to the interaction of susceptible with infected human. The least sensitive parameter is the rate of recruitment/death of human population.

3.4. Local Stability of Disease Free Equilibrium Point

The stability of disease free equilibrium point is established by linearizing system (6) around the disease free equilibrium. Using the reduced system of Equation (6), the model will be linearized to obtain the Jacobian matrix.

(18)

The characteristic equation corresponding to is given by;

. (19)

where;

(20)

. (21)

(22)

The three eigenvalues have negative real parts if they satisfy the Routh-Hurwitz Criteria, that is;

If, then

(23)

It was shown that, , and According to the Routh-Hurwitz Criteria, it follows that the disease-free equilibrium of the reduced model (6) is locally asymptotically stable.

3.5. Endemic Equilibrium Point

The endemic equilibrium points (EEP) of the reduced model equation system (6) is given by. For EEP, it is assumed that the disease exists in the population for.

and satisfies the following relations;

. (24)

. (25)

is the solution of the following quadratic polynomial;

(26)

where

,

,

,

From the Equation (26) it follows that

We can check from the quadratic (26) for the possibility of existence of multiple equilibria. It is important to note that the coefficient A is always positive and C is positive if is less than unity, and negative if is greater than unity, whenever from the polynomial (26). Hence, we establish the following results:

There are precisely two endemic equilibria if,.

From this result we state the theorem which will be proved by using bifurcation diagram and centre manifold theorem.

Theorem 1. The two endemic equilibrium points exist if and are locally stable if and unstable if.

Determination of Forward or Backward Bifurcation

The existence of endemic equilibrium which is locally stable for and unstable if was explored by a forward bifurcation diagram obtained when a graph of human infected by MU “x” against reproduction number “” was drawn as shown below.

From Figure 2, the two equilibrium points exchange stability depending on the value of. A forward bifurcation in the equilibrium points occur at. When, no endemic equilibrium solution exists and the disease free equilibrium is the only local attractor. But when, the endemic equilibrium exists and is the only local attractor. Thus there is a forward bifurcation because in the neighbourhood of the bifurcation point, the endemic disease prevalence is an increasing function of.

The local asymptotic stability of endemic equilibrium is analysed by using the centre manifold theory [4] and shows that the reduced model system (6) exhibit a forward bifurcation at as shown in Figure 2 and is locally stable.

3.6. Summary

The model without control was formulated using a system of ordinary differential equations. The model was qualitatively analysed for the existence and stability of the disease-free equilibrium point and endemic equilibrium point. The reproduction number was calculated using next generation method. The disease-free equilibrium point was shown to be locally asymptotically stable. The endemic equilibrium point exists for. The sensitivity analysis showed that the rate of MU infection (and) due to the interaction of human and water-bugs populations stimulated the transmission of the infection in the population.

The model was further extended with incorporation of control so as to reduce the transmission dynamics of MU infection.

3.7. Model Equations with Control Variables

Now the model Equations (6) is extended to incorporate time-dependent controls to obtain the following system:

(27)

In the system (27) two control variables and have been introduced. The function is a control effort to minimize MU infection in human population through environmental and health education for prevention while the function is the control to minimize MU infection in water-bugs through water and environmental purification rate.

Analysis of the Optimal Control Problem

It is intended to minimize the MU infection on human caused by the interaction between susceptible human and infected vector (water-bugs), as well as minimizing MU infection on vector (water-bugs) caused by water contamination. To investigate the optimal level of effort that would be needed to control the disease, first we formulate the objective functional J which is defined by choosing a quadratic cost on the controls as follows:

(28)

where is the final time, and are weight factors associated by infected human and infected water-bugs respectively while and are weight factors linked to control variables and respectively.

The choice of quadratic control in the objective function is simply because we need to minimize the MU infection as well as minimize the cost on the control. The goal is to minimize the MU infection in human population and in water-bugs while minimizing the cost of controls. We seek optimal controls such that:

where the control set is measurable and

The term is the cost of control efforts in minimizing the MU infection to human, is the control efforts on minizing MU infection to water-bugs. The necessary conditions that an optimal control problem must satisfy come from the Pontryagin’s Maximum Principle [8] . This principle converts (19) and (20) to a problem of minimizing Hamiltonian function H, defined by

(29)

where are the adjoint variables or co-state variables. By applying the Pontryagin’s maximum principle and the existence of optimal control problem, we have the following theorem [9] :

Theorem 2. There exists an optimal control, and corresponding solution, that minimizes over U. Moreover, there exist adjoint functions, satisfying

(30)

with the transversality conditions and the controls satisfying the optimality conditions

(31)

To find we first solve the optimality conditions given by

.

We differentiate Equation (21) with respect to to get

(32)

We therefore solve for by equating as described by [10] .

By equating system (24) to zero we obtain

,

.

From the system (23) then. Hence the optimality conditions is written as

(33)

By standard control arguments involving the bounds on the controls, we conclude similarly as [10] that

and (34)

According to the prior boundedness of the state system, the adjoint system and the resulting Lipschitz structure of the ODEs the uniqueness of the optimal control for small is obtained. The uniqueness of the optimal control follows from the uniqueness of the optimality system that consist of Equation (19), Equation (22) and transversality condition with characterization (25).

There is a restriction on the length of time interval in order to guarantee the uniqueness of the optimality system. This smallness restriction of the length on the time due to the opposite time orientations of the optimality system; the state problem has initial values and the adjoint problem has final values. This restriction is common in control problems [10] .

4. Numerical Simulation for the Optimal Control

In order to illustrate the analytical results of the study, numerical simulations of the model equations with control variables (27) are carried out using the set of parameter values below:

In Figures 3-6, we use the following weight factors throughout, and the initial state variables and the parameter values in Table 2 to illustrate the effect of various optimal strategies on the transmission dynamics of MU. The graphs are labelled as follows: A (Human infected by MU), B (Water-bugs infected by MU), C (Water contamination) and D (Control profile).

Figure 3 shows simulation of the model when both controls are set to zero.

From Figure 3, the simulations of model show that when both controls are set to zero, no effect arises for graphs A, B and C while graph D shows that when the controls are set to zero, then the infected water-bugs increase with time. The infected human also increases with time and the rate of water contamination always increases.

Figure 4 shows the simulation of the model with only one control (environmental and health education).

Figure 4 shows the situation whereby only the control (environmental and health education) is used to optimize the objective functional J while the control (water and environmental purification) is set to zero. It is observed that although the rate of water contamination in Figure 4(c) is still increasing, this control strategy results in a significant decrease of the number of human infected by MU as shown in Figure 4(a), compared with the case without control. For Figure 4(b) it shows that there is no significant difference between the graph with control (blue in colour) and the graph without control (red in colour) because control is set to zero, then this strategy results also in a significant increase in the number of water-bugs infected by MU.

For the control profile as shown in Figure 4(d), control is at the upper bound at the beginning before dropping to the lower bound at the final time and the control remain at the lower bound till the final time.

Figure 5 shows the simulation of the model with one control “” (water and environmental purification) is optimized.

Figure 5, shows the strategy whereby only the control (water and environmental purification) is used to optimize the objective functional J while the control (environmental and health education) is set to zero. We observe that although the water contamination in Figure 5(c) is still increasing, this control strategy results in a significant decrease in the number of water-bugs infected by MU (Figure 5(b)) compared with the results of the graph without control. Also the number of human infected by MU with control decreases (Figure 5(a)). This happens because control was applied to infected water-bugs (vector). It shows that eliminating the spread of the MU infection in water-bugs population would lead to an indirect reduction of MU infection among the human population.

For the control profile as shown in Figure 5(d), control is at the upper bound up to the final time before dropping to the lower bound and the control remain at the lower bound till the final time.

Figure 6 show the simulation of the model whereby both controls and are optimized.

Figure 6 show the optimal use of control (environmental and health education) and control (environmental and water purification rate). We use both two controls and to optimize the objective function J. It is observed in Figure 6(a) and Figure 6(b) that due to the control strategies, although water contamination is still high but the number of water-bugs infected by MU decreases in the population and at the same time the number of human infected by MU decreases. As we aimed on minimizing the MU infection on human and water-bugs, hence we are satisfied with the results.

Control profile in Figure 6(d) shows that control is at the upper bound for 28 months before dropping to

the final time while was at the upper bound until the final time before dropping to the lower bound.

5. Discussion and Conclusion

In this paper, a deterministic model for the transmission dynamics of MU infection was derived and analysed. The model incorporates the assumption that MU infection arises in the population through the interaction of human population and water-bugs population (susceptible human interacting with infected water-bugs or susceptible water-bugs interacting with infected human). The basic reproduction number was calculated and examined. Also the existence and stability of equilibrium points were examined. Optimal control analysis of the model was finally performed. The model showed that the disease free equilibrium is locally stable by using Routh-Hurwith criteria at threshold parameter less than unity and unstable at threshold parameter greater than unity. The analysis showed that the existence of multi-equilibria for endemic is locally stable when the threshold parameter exceeds unity. This is due to the existence of forward bifurcation at threshold parameter equal to unity. Numerical sensitivity analysis showed that the parameter is the most sensitive on and the least sensitive parameter is. Applying optimal control, the conditions for optimal control of the MU infection with control were derived and analysed, to employ environmental and health education to people for prevention and control to apply water and environmental purification rate. From our numerical results it was established that, application of optimal control leads to the decrease of the number of infected water-bugs and also decreases the number of human infected by MU. This was due to the interaction of human population and water-bugs population. If we would control only one population―human population infected by MU, we could not get good results when we optimized only control for human infected by MU. In Figure 4(a), it was observed that there was a temporary decrease of infection, but when we optimized both controls it was found that there was permanent decrease of the MU infection. Based on the results of this study, it is concluded that the best way of minimizing the transmission of MU infection is to apply optimal control on environmental and health education in human for prevention, for instance people have to be educated on how they can protect their environment to overcome environmental contamination like preventing arsenic from reaching water bodies. Also people should be provided with health education, such as wearing protective clothing against water-bugs while working around the breeding grounds of the water-bugs, and not exposing themselves to contaminated environment. To preserve water and environment with arsenic (As) concentration by purifying water and environment, the public health sectors should be familiar with the disease and let the community know about the infection, its transmission, symptoms and prevention, and also it should establish policies programmes control of the MU infection by taking into consideration the aspect of environmental and health education for MU prevention. Awareness campaigns should be conducted to the community to undertake practices which can limit the transmission of MU infection, by encouraging them on the issue of cleaning environment and limit arsenic (As) contamination with water.

Cite this paper

Magreth AngaKimaro,Estomih S.Massawe,Daniel OluwoleMakinde, (2015) Modelling the Optimal Control of Transmission Dynamics of Mycobacterium ulceran Infection. Open Journal of Epidemiology,05,229-243. doi: 10.4236/ojepi.2015.54027

References

NOTES

^*Corresponding author.