Open Journal of Civil Engineering
Vol.06 No.03(2016), Article ID:65835,11 pages
10.4236/ojce.2016.63028
Shape Control and Vibration Analysis of Piezolaminated Plates Subjected to Electro-Mechanical Loading
Rajan L. Wankhade1, Kamal M. Bajoria2
1Applied Mechanics Department, Government College of Engineering, Karad, India
2Department of Civil Engineering, Indian Institute of Technology Bombay, Mumbai, India

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 March 2016; accepted 22 April 2016; published 25 April 2016
ABSTRACT
Shape control and free vibration analysis of piezolaminated plates subjected to electro mechanical loading are evaluated using finite element method. First order shear deformation theory is employed in the analysis. Both extensions as well as shear actuators are considered for piezolaminated plates. Rectangular four node isoparametric element is used in the finite element formulation. Variation of temperature is neglected for the orthotropic layers of the laminate and for piezolayer. Annular circular plates and rectangular plates with piezoelectric layers mounted and/or integrated are analysed for various parameters. Numerical results are presented for varying the actuator voltage for annular plates with different thicknesses of piezo patches. In case of rectangular plate shear actuator is considered for vibration analysis.
Keywords:
Piezoelectric Material, Finite Element Analysis, Shape control, Vibrational Analysis

1. Introduction
In recent years the use of smart piezolaminated composite structures has been increased. Due to their significant stiffness and low weight many isotropic materials and structures are now replaced by piezolaminated smart composites. The piezoelectric ceramics are available in the form of thin sheets which can be surface mounted and/or integrated with the laminates to control the structural response in shape, vibration and buckling. Suffieforts are directed towards the analysis of such piezoelectric laminated structures. It has gained an attraction toward the shape and vibration control of piezoelectric laminates which have the capability of active and passive control. Ha et al. (1992) performed finite element analysis of composite structures containing distributed piezoceramic sensors and actuators [1] . Hwang and Park (1993) studied finite element modeling of piezoelectric sensors and actuators and provided results for piezoelectric laminates [2] . Li and Bainum carried out vibration control analysis of flexible spacecraft integrating a momentum exchange controller and a distributed piezoelectric actuator [3] . Tzou and Zhou (1995) performed dynamics analysis and control of non-linear circular plates with piezoelectric actuators [4] . Thomson and Loughlan (1995) examined the active buckling control of some composite column using piezoceramic actuators [5] . Kim et al. (1996) developed finite element model for a smart cantilever plate and comparison also performed experimental analysis [6] . Batra and Liang (1997) investigated the vibrations of a rectangular laminated elastic plate with embedded piezoelectric sensors and actuators [7] . Agrawal et al. (1997) performed analysis of adaptive antenna for shape control using piezoelectric actuators [8] . Soares et al. (1999) carried out optimal design of piezolaminated structures [9] . Faria and Almeida (1999) studied enhancement of pre-buckling behavior of composite beams with geometric imperfections using piezoelectric actuators [10] . Sze and Yao (2000) used a hybrid stress ANS solid-shell element and its generalization for smart structure modeling [11] . Wang et al. (2001) performed vibration control of smart piezoelectric composite plates [12] . Cen et al. (2002) developed a new 4-node quadrilateral FE model with variable electrical degrees of freedom for the analysis of piezoelectric laminated composite plates [13] .
Moita et al. (2004) studied active control of adaptive laminated structures with bonded piezoelectric sensors and actuators. [14] . Artel and Becker (2005) investigated coupled and uncoupled analyses of piezoelectric free-edge effect in laminated plates [15] . Oh and Lee (2006) carried out analysis for supersonic flutter suppression of piezolaminated cylindrical panels based on multifield layerwise theory [16] . Ray and Balaji (2007) performed active structural acoustic control of laminated cylindrical panels using smart damping treatment [17] . Periasamy (2008) performed shape control of composite structures with optimally placed piezoelectic patches [18] . Ly et al. (2011) developed modeling and studied characterization of piezoelectric cantilever bending sensor for energy harvesting [19] . Kamal M. Bajoria and Rajan L. Wankhade (2012) analyzed rectangular piezolaminated plates for free vibration using Finite Element Method [20] . Wankhade and Bajoria (2013) developed finite element modeling for free vibration and buckling analysis of piezolaminated plates using higher order shear deformation theory [21] [22] . Brighenti (2014) studied smart behaviour of layered plates through the use of auxetic materials [23] . Bajoria and Wankhade (2015) performed vibration control of cantilever piezolaminated beam with extension and shear mode piezo actuators [24] . Kerboua et al. (2015) further carried out vibration control of beam using piezoelectric-based smart material [25] . Zhang et al. (2015) studied active vibration control of piezoelectric bonded smart structures using PID algorithm [26] . Bendine and Wankhade studied vibration control of FGM piezoelectric plate based on LQR genetic search where analysis was performed for different sets of power law exponent [27] .
Here shape control and vibration analysis of piezolaminated plates subjected to combined action of electrical and mechanical loading is carried out considering first order shear deformation theory. Finite element method as employed for the analysis purpose. An isoperimetric four noded rectangular element is used in the finite element formulation. Shape control of annular plate with piezo patched at optimal locations is performed for varying the actuator voltage. Again the thickness of piezolayer is varied and response of structure is studied. Further in case rectangular plate shear piezoelectric actuator is considered for the vibration analysis. Results are presented considering shape control and vibration piezolaminated plate for different parameters viz. actuator voltage, aspect ratio of plate and varying thickness of piezolayer.
2. Mathematical Formulation
2.1. Equilibrium and Incremental Equations
Virtual displacement principle is considered in the mathematical formulation to obtain equation s of equilibrium. Equilibrium between internal and external forces has to be satisfied. If  represents the vector of the sum of the internal and external forces. Then equilibrium can be written as follow:
represents the vector of the sum of the internal and external forces. Then equilibrium can be written as follow:
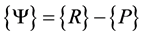 (1)
(1)
In above equation, {R} is the external forces due to imposed load and {P} represents the vector of internal resisting forces. For piezolaminated plates the equilibrium equation can be written as:
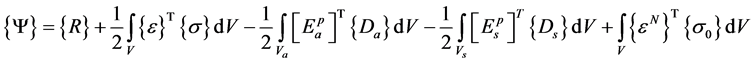 (2)
(2)
where V, Vs and Va represents the area of the entire structure, sensor layer and actuator layer respectively. For writing the work done by external forces due to the applied surface traction and applied electric charge on actuator, the equation for external work done {R} can be summarized as:
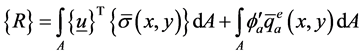 (3)
(3)
2.2. Finite Element Modeling
Finite element modeling is considered for the analysis purpose. Here displacement field considered in finite element formulation is based on first order shear deformation theory. Hence considering the effect of shear deformation, displacement field of first order shear deformation theory is written as follow:

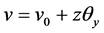
 (4)
(4)
where,  and
and 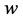 are the displacement of any point in the plate domain in x, y and z direction respectively.
are the displacement of any point in the plate domain in x, y and z direction respectively. 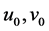 and
and  are the displacement of midpoint of normal.
are the displacement of midpoint of normal.  are the rotations of normal at the middle plane in x and y direction about y and x axis respectively.
are the rotations of normal at the middle plane in x and y direction about y and x axis respectively.
The strains associated with the displacement model for linear bending are given by
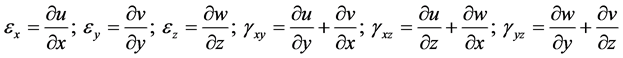 (5)
(5)
Figure 1 shows general piezolaminated plate with actuator and sensor patches at the top and bottom surface of the plate. Fiber can be oriented with reference to the horizontal axes and is modelled in finite element formulation.
2.2.1. Shell Element and Shape Functions
Four nodded isoparametric rectangular element is adopted as shown in Figure 2.
Shape functions are given as:
Figure 1. Piezolaminated plate with actuator and sensor layers at the top and bottom surface of the plate.

Figure 2. Four nodded isoparametric element. (a) Rectangular element; (b) Mapping of element.
2.2.2. Displacement Field
The displacement field associated with the eight nodded rectangular element is given as:

2.2.3. Strain within the Element
Strains associated with the displacement field can be written as follow:
a. Middle plane membrane strains

in which 


Curvature strains/Bending strains.
Curvature strains are linearly related to bending displacement as:

Shear strains,

Thus

and shear strains can separately be written as,

In which 


Hence strain displacement relationship can be obtained as:

2.3. Electro-Mechanical Coupling
For piezolaminated plates two constitutive relationships exist which includes the effect of mechanical and electrical loading as given by Eq. 17. Variation of temperature effect is neglected in formulation.

In which,

where, {D} is electric displacement vector, [e] is dielectric permittivity matrix, 



Electrical Potential Function


where, 



2.4. Stiffness Matrix Equations
Element stiffness matrix is written as,

where,


In which,



and

And hence element equation in the form of global stiffness matrix can be written as:

2.5. Free Vibration Equation
For free vibration problems, the equations of motion can be expressed as the following eigenvalue problem

where, the lowest magnitude of eigenvalue gives critical buckling load and the vector 
3. Results and Discussions
3.1. Shape Control of Annular Plate with Piezoelectric Patches
A shape control of clamped annular plate having diameter 1 m is analyzed subjected to electrical load. Here no mechanical load is provided to the structure. Figure 3 shows geometry of the clamped annular plate with piezoelectric patches provided on the surface of the plate. These piezoelectric patched are attached at specified location of plate Periasamy (2008) has analyzed the same annular plate with actuator voltage 45 only having constant tplate/tpiezo ratio [18] . Here the analysis of annular plate is carried out considering different actuator voltage of piezolaminated actuator. Plate is modelled with 4-noded rectangular element with different elements and results are shown in Table 1 and Table 2. It is found that 180 elements are sufficient to satisfy convergence criteria.
Figure 3. Geometry and modeling of clamped annular plate with piezoelectric patches.
Table 1. Convergence results with different plate element for a plate (Tplate/Tpiezo = 1.5).
Table 2. Convergence results with different plate element for a plate (Tplate/Tpiezo = 2.0).
Hence a convergence study is included to show that these numbers of elements are sufficient to get the realistic results and no need to go for higher number of elements. Figures 4-8 show deflection of the plate along its radius with varying actuator voltage (AV 20, AV 40 and AV 60) for different Tplate/Tpiezo ratio as 1.5, 2. Material properties are adopted as follows:
For graphite epoxy composite
For PZT G-1195
The maximum tip displacements observed at end are 3.09E−4 and 6.17E−4 and 9.26E−4 for AV 20, AV 40 and AV 60 respectively with Tplate/Tpiezo = 1.5. It is observed that increase in actuator voltage leads to considerable increase in end deflection. About 50% increase in deflection at the tip is found for AV40 as compared to that of AV 20. Also if we consider the thickness of plate to thickness of piezolayer ratio, about 57.2% increase in deflection is observed at free end as tplate to tpiezolayer ratio increases from 1.5 to 2.0. Thus either increase voltage or increase thickness of piezolayer it will have influence on shape control of structure.
Figure 4. Undeformed and deformed shape of plate with actuator voltage 20 (Tplate/Tpiezo = 1.5).
Figure 5. Undeformed and deformed shape of plate with actuator voltage 40 (Tplate/Tpiezo = 1.5).
Figure 6. Undeformed and deformed shape of plate with actuator voltage 60 (Tplate/Tpiezo = 1.5).
Figure 7. Deflection along the radius with varying actuator voltage (Tplate/Tpiezo = 1.5).
3.2. Free Vibration Analysis of Piezolamonated Plate with PZT Shear Actuator
A simply supported piezolaminated plate with the top and bottom layers made of 00 graphite-epoxy and the central layer made of axially poled PZT-5A thus having laminated scheme as [00 Gr-Epoxy/PZT-5A/00 Gr-Epoxy] is examined for free vibration. Length of the plate is taken as 0.25 m. Table 3 shows elastic and piezoelectric properties of the laminate. The natural frequencies for different L/H ratio is presented in table 4. Total thickness of laminate is taken as “H”, whereas the thickness of graphite-epoxy and that of PZT-5A are taken as 0.4H and 0.2H respectively.
Table 4 shows natural frequencies in Hz for [Gr-epoxy/PZT-5A/ Gr-epoxy] simply supported shear actuated piezolaminated plate with closed loop and open loop electric condition. Maximum variation in frequency is found as 2.85% for closed loop as that of open loop.
Vibration analysis of piezoelectric laminated plate is carried out for different aspect ratio of plate. Piezolaminated plates are analysed for different electric condition of the piezolayer.
Table 3. Elastic and piezoelectric properties for Graphite-Epoxy and PZT-5A.
Table 4. Natural frequencies (Hz) of [Gr-epoxy/PZT-5A/Gr-epoxy] simply supported shear actuated piezolaminated plate.
Figure 8. Deflection along the radius with varying actuator voltage (Tplate/Tpiezo = 2.0).
4. Conclusion
In the present analysis, shape control and vibration of piezolaminated plates subjected to electro mechanical loading are studied based on finite element method. First order shear deformation theory is used for the same purpose. Both extensions as well as shear actuators are considered for two problems of piezolaminated plates. Annular circular plate and rectangular plates with piezoelectric layers mounted and/or integrated are analysed for various parameters. Numerical results are presented for varying the actuator voltage for annular plates with different thicknesses of piezo patches. In case of rectangular plate shear actuator is considered for vibration analysis. The maximum tip displacements observed at end are 3.09E−4 and 6.17E−4 and 9.26E−4 for AV 20, AV 40 and AV 60 respectively with Tplate/Tpiezo = 1.5. Again the maximum tip displacements observed at end are 2.31E−4 and 4.63E−4 and 6.94E−4 for AV 20, AV 40 and AV 60 respectively with Tplate/Tpiezo = 2.0. It is observed that increase in actuator voltage leads to considerable increase in end deflection. About 50% increase in deflection at the tip is found for AV40 as compared to that of AV 20 for same thickness of piezolayer. Also if we consider same voltage then deflection reduces for increasing thickness rations of plate to that of piezolayer. It is observed that with proper selection and placement of piezoelectric actuators as extension or shear, it is possible to generate enough forces on a structure in order to control its response in shape and vibration.
Cite this paper
Rajan L. Wankhade,Kamal M. Bajoria, (2016) Shape Control and Vibration Analysis of Pi-ezolaminated Plates Subjected to Electro-Mechanical Loading. Open Journal of Civil Engineering,06,335-345. doi: 10.4236/ojce.2016.63028
References
- 1. Ha, S.K., Keilers, C. and Chang, F.K. (1992) Finite Element Analysis of Composite Structures Containing Distributed Piezoceramic Sensors and Actuators. AIAA Journal, 30, 772-780.
http://dx.doi.org/10.2514/3.10984 - 2. Hwang, W.S. and Park, H.C. (1993) Finite Element Modeling of Piezoelectric Sensors and Actuators. AIAA Journal, 31, 930-937.
http://dx.doi.org/10.2514/3.11707 - 3. Li, Z. and Bainum, P.M. (1994) Vibration Control of Flexible Spacecraft Integrating a Momentum Exchange Controller and a Distributed Piezoelectric Actuator. Journal of Sound and Vibration, 177, 539-553.
http://dx.doi.org/10.1006/jsvi.1994.1450 - 4. Tzou, H.S. and Zhou, Y.H. (1995) Dynamics and Control of Non-Linear Circular Plates with Piezoelectric Actuators. Journal of Sound and Vibration, 188, 189-207.
http://dx.doi.org/10.1006/jsvi.1995.0586 - 5. Thomson, S.P. and Loughlan, J. (1995) The Active Buckling Control of Some Composite Column Using Piezoceramic Actuators. Composite Structures, 32, 59-67.
http://dx.doi.org/10.1016/0263-8223(95)00048-8 - 6. Kim, J., Varadan, V.V., Varadan, V.K. and Bao, X.Q. (1996) Finite Element Modeling of a Smart Cantilever Plate and Comparison with Experiments. Smart Materials and Structures, 5, 165-170.
http://dx.doi.org/10.1088/0964-1726/5/2/005 - 7. Batra, R.C. and Liang, X.Q. (1997) The Vibration of a Rectangular Laminated Elastic Plate with Embedded Piezoelectric Sensors and Actuators. Computers and Structures, 63, 203-216.
http://dx.doi.org/10.1016/S0045-7949(96)00349-5 - 8. Agrawal, B.N., Elshafei, M.A. and Song, G. (1997) Adaptive Antenna Shape Control Using Piezoelectric Actuators. Acru Astronautica, 40, 821-826.
http://dx.doi.org/10.1016/S0094-5765(97)00185-9 - 9. Soares, C.M.M. and Correia, V.M.F. (1999) Optimal Design of Piezolaminated Structures. Composite Structures, 47, 625-634.
http://dx.doi.org/10.1016/S0263-8223(00)00036-2 - 10. Faria, A.R. and Almeida, S.F.M. (1999) Enhancement of Pre-Buckling Behavior of Composite Beams with Geometric Imperfections Using Piezoelectric Actuators. Composites Part B, 30, 43-50.
http://dx.doi.org/10.1016/S1359-8368(98)00047-X - 11. Sze, K.Y. and Yao, L.Q. (2000) A Hybrid Stress ANS Solid-Shell Element and Its Generalization for Smart Structure Modeling: Part I Solid Shell Element Formulation. International Journal for Numerical Methods in Engineering, 48, 545-564.
http://dx.doi.org/10.1002/(SICI)1097-0207(20000610)48:4<545::AID-NME889>3.0.CO;2-6 - 12. Wang, S.Y., Quek, S.T. and Ang, K.K. (2001) Vibration Control of Smart Piezoelectric Composite Plates. Smart Materials and Structures, 10, 637-644.
http://dx.doi.org/10.1088/0964-1726/10/4/306 - 13. Cen, S., Soh, A.K., Long, Y.Q. and Yao, Z.H. (2002) A New 4-Node Quadrilateral FE Model with Variable Electrical Degrees of Freedom for the Analysis of Piezoelectric Laminated Composite Plates. Composite Structures, 58, 583-599.
http://dx.doi.org/10.1016/S0263-8223(02)00167-8 - 14. Moita, J.M.S., Correia, I.F.P., Soares, C.M. and Soares, C.A.M. (2004) Active Control of Adaptive Laminated Structures with Bonded Piezoelectric Sensors and Actuators. Computers and Structures, 82, 1349-1358.
http://dx.doi.org/10.1016/j.compstruc.2004.03.030 - 15. Artel, J. and Becker, W. (2005) Coupled and Uncoupled Analyses of Piezoelectric Free-Edge Effect in Laminated Plates. Composite Structures, 69, 329-335.
http://dx.doi.org/10.1016/j.compstruct.2004.07.015 - 16. Oh, I.K. and Lee, I. (2006) Supersonic Flutter Suppression of Piezolaminated Cylindrical Panels Based on Multifield Layerwise Theory. Journal of Sound and Vibration, 291, 1186-1201.
http://dx.doi.org/10.1016/j.jsv.2005.07.033 - 17. Ray, M.C. and Balaji, R. (2007) Active Structural Acoustic Control of Laminated Cylindrical Panels Using Smart Damping Treatment. International Journal of Mechanical Sciences, 49, 1001-1017.
http://dx.doi.org/10.1016/j.ijmecsci.2007.02.001 - 18. Periasamy, R. (2008) Shape Control of Composite Structures with Optimally Placed Piezoelectic Patches. Ms Thesis, University of Waterloo, Ontario.
- 19. Ly, R., Rguiti, M., D’Astorg, S., Hajjaji, A., Courtois, C. and Leriche, A. (2001) Modeling and Characterization of Piezoelectric Cantilever Bending Sensor for Energy Harvesting. Sensors and Actuators A: Physical, 168, 95-100.
http://dx.doi.org/10.1016/j.sna.2011.04.020 - 20. Bajoria, K.M. and Wankhade, R.L. (2012) Free Vibration of Simply Supported Piezolaminated Composite Plates Using Finite Element Method. Advanced Materials Research, 587, 52-56.
http://dx.doi.org/10.4028/www.scientific.net/AMR.587.52 - 21. Wankhade, R.L. and Bajoria, K.M. (2013) Buckling Analysis of Piezolaminated Plates Using Higher Order Shear Deformation Theory. International Journal of Composite Materials, 3, 92-99.
- 22. Wankhade, R.L. and Bajoria, K.M. (2013) Free Vibration and Stability Analysis of Piezolaminated Plates Using Finite Element Method. Smart Materials and Structures, 22, Article ID: 125040.
http://dx.doi.org/10.1088/0964-1726/22/12/125040 - 23. Brighenti, R. (2014) Smart Behaviour of Layered Plates through the Use of Auxetic Materials. Thin walled Structures, 84, 432-442.
http://dx.doi.org/10.1016/j.tws.2014.07.017 - 24. Bajoria, K.M. and Wankhade, R.L. (2015) Vibration of Cantilever Piezolaminated Beam with Extension and Shear Mode Piezo Actuators. Proceedings of SPIE, Active and Passive Smart Structures and Integrated Systems, 9431, 943122.
- 25. Kerboua, M., Megnounif, A., Benguediab, M., Benrahou, K.H. and Kaoulala, F. (2015) Vibration Control Beam Using Piezoelectric-Based Smart Materials. Composite Structures, 123, 430-442.
http://dx.doi.org/10.1016/j.compstruct.2014.12.044 - 26. Zhang, S., Schmidt, R. and Qin, X. (2015) Active Vibration Control of Piezoelectric Bonded Smart Structures Using PID Algorithm. Chinese Journal of Aeronautics, 28, 305-313.
http://dx.doi.org/10.1016/j.cja.2014.12.005 - 27. Bendine, K. and Wankhade, R.L. (2016) Vibration Control of FGM Piezoelectric Plate Based on LQR Genetic Search. Open Journal of Civil Engineering, 6, 1-7.
http://dx.doi.org/10.4236/ojce.2016.61001














