Open Journal of Civil Engineering
Vol.05 No.02(2015), Article ID:56392,20 pages
10.4236/ojce.2015.52016
Seismic Capacity Assessment of Existing RC Buildings in The Sudan by Using Pushover Analysis
Mohammed Ismaeil1, Mohamed Sobaih2, Adel Akl2
1Cairo University, Cairo, Egypt
2Department of Structural Engineering, Cairo University, Cairo, Egypt
Email: abunama79@hotmail.com, msobaih2@yahoo.com, adelakl@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 31 March 2015; accepted 15 May 2015; published 18 May 2015
ABSTRACT
Recently, the evaluation of seismic performance of existing buildings has received a great attention. Current research works and observations indicate that The Sudan have low-to-moderate seismic regions. Most of existing buildings are designed only for gravity load. The objective of this paper is to assess the seismic performance of existing RC buildings in The Sudan. Four typical buildings were investigated using pushover analysis according to ATC-40. They were designed according to the Regulations for earthquake-resistant design of buildings in Egypt (ESEE) and International Building Code (IBC2012). Results showed that the buildings designed considering by ESEE and IBC2012 loads were found adequate and satisfied the Immediate Occupancy (IO) acceptance criteria according to ATC-40. The comparison of the pushover curve shows that the stiffness of frames is larger when using ESEE Regulations compared to the IBC2012 design. This means that ESEE design procedure provides a greater capability to resist seismic load than the IBC2012 design.
Keywords:
Pushover Analysis, Seismic Capacity, The Sudan, Assessment, RC Buildings

1. Introduction
The Sudan is not free from earthquakes. It has experienced many earthquakes during the recent history, and the previous studies in this field demonstrate this argument [1] . Most of existing buildings in The Sudan do not meet the current design standards due to design shortage or construction shortcomings. There are various reasons such as there is no seismic code in The Sudan. Therefore, existing buildings should be evaluated regarding their capacity for resisting expected seismic effects. To estimate seismic demands for a building, the structural engineering profession is now using the non-linear static procedure, known as pushover analysis. It is a commonly used technique, which provides acceptable results [2] .
Pushover analysis is a series of incremental static analysis carried out to develop a capacity curve for the building. This procedure needs the execution of a nonlinear static analysis of the structure that allows the monitoring of the progressive yielding of the structure component [3] .
The building is subjected to a lateral load. The load magnitude increases until the building reaches the targeted displacement. This target displacement is determined to represent the top displacement when the building is subjected to design level ground excitation. Pushover analysis produces a pushover curve or capacity curve that presents the relationship between the base shear 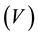 and roof displacement
and roof displacement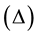 . The Pushover curve depends on the strength and deformation capacities of the structure and describes how the structure behaves beyond the elastic limit [4] . Many researchers have conducted studies in this area such as:
. The Pushover curve depends on the strength and deformation capacities of the structure and describes how the structure behaves beyond the elastic limit [4] . Many researchers have conducted studies in this area such as:
Jitendra et al. (2012) [5] , presented a research paper on “Pushover Analysis of Unsymmetrical Framed Structures on Sloping Ground”. The paper deals with non-linear analysis of various symmetric and asymmetric structures constructed on plain subjected to various kinds of loads .The analysis has been carried out using SAP2000 and ETABS software. The paper concludes that the structure with vertical irregularity is more critical than a structure with plan irregularity.
Golghate et al. (2013) [6] , carried out “a Pushover Analysis of a 3 Storey’s Reinforced Concrete Building” aiming to evaluate the zone-IV selected reinforced concrete building to conduct non-linear static analysis (pushover analysis) using SAP 2000. The study shows that hinges have developed in the beams and columns showing the three stages immediate occupancy, life safety and collapse prevention.
Rahul et al. (2004) [7] , performed a pushover analysis on a 19 story, slender concrete tower building located in San Francisco with a gross area of 430,000 square feet. The lateral system of this building consists of concrete shear walls and it is designed conforming to 1997 Uniform Building Code (UBC), and pushover analysis is performed to verify code’s underlying intent of Life Safety performance under design earthquake. Utilizing the results from the analysis, some modifications are made to the original code-based design so that the design objective of Life Safety performance is expected to be achieved under design earthquake.
In 2012, 2013 and 2014 Ismaeil, et al. (the first Author of this paper) presented a series of earthquake researches such as: Proposed Methodology for Seismic Evaluation and Strengthening of Existing School Buildings in The Sudan [8] , Assessment of Seismic Performance and Strengthening of RC Existing Residential Buildings in The Sudan [9] , Seismic Retrofitting of a RC Building by Adding Steel Plate Shear Walls [10] , Pushover Analysis of Existing 3 Stories RC Flat Slab Building in The Sudan [11] , Pushover Analysis of Existing 4 Storey RC Flat Slab Building [12] . These studies are conducted to investigate the performance of samples of existing RC buildings in The Sudan.
2. Evaluation of Seismic Performance of Existing Buildings
Most buildings and structures in The Sudan have not yet been designed and constructed in compliance with earthquake provisions or given any consideration for earthquake effect.
2.1. Earthquake Loads
The earthquake loads are calculated following the rules which are given in the International Building Code (IBC2012) [13] , and Regulations for earthquake-resistant design of buildings in Egypt, 1988 these regulations have been prepared by the Egyptian Society for Earthquake Engineering (ESEE) [14] .
2.1.1. Seismic Loads According to IBC2012
The horizontal seismic loads are defined according to IBC2012. The lateral force effect on the structure can be translated to equivalent lateral force at the base of the structure which can be distributed to different stories. According to IBC2012, the total seismic base shear force  is determined as follows:
is determined as follows:
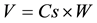 (1)
(1)
where: Cs is the seismic coefficient, W is the total weight and 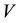 is the base shear. The seismic design coefficient (Cs) shall be determined in accordance with the following equation:
is the base shear. The seismic design coefficient (Cs) shall be determined in accordance with the following equation:
 (2)
(2)
where, SDS = Design spectral response acceleration in the short period range
R = Response modification factor.
I = Occupancy importance factor determined.
The value of the seismic response coefficient, (Cs), need not be greater than the following equation:
 (3)
(3)
But shall not be taken less than.
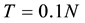 (4)
(4)
where N = Number of stories
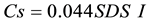 (5)
(5)
where, SDS = Design spectral response acceleration at a period of 1 sec.
T = Fundamental period of the structure (sec).
Design earthquake spectral response acceleration at short periods, SDS, and at 1-sec period, SD1, shall be as follows.
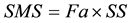 (6)
(6)
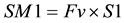 (7)
(7)
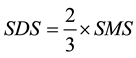 (8)
(8)
 (9)
(9)
where:
SS: the maximum spectral response acceleration at short periods.
S1: the maximum spectral response acceleration at a period of 1 sec.
Fa: acceleration-based site coefficient.
Fv: velocity-based site coefficient.
SMS: the maximum spectral response acceleration at short periods adjusted for site class.
SM1: the maximum spectral response acceleration at a period of 1 sec adjusted for site class.
SDS: the design spectral response acceleration at short periods.
SD1: the design spectral response acceleration at a period of 1 sec.
Mapped Acceleration Parameters
The design parameters that are used in the equivalent static method are illustrated as following: The parameters Ss and S1 shall be determined from the 0.2 and 1 second spectral response accelerations shown on country maps
Where S1 is less than or equal to 0.04 and Ss is less than or equal 0.15, the structure is permitted to be assigned to seismic design category A So,
S1= the mapped spectral accelerations for a 1-second period/
Ss= the mapped spectral accelerations for short period.
On lack of a map of spectral accelerations of S1 and SS, the following can be assumed: S1 = 1.25 Z, Ss = 2.5 Z (amendment no. 3 to SI 413 (2009)).
Vertical Distribution of Base Force
The buildings are subjected to a lateral load distributed across the height of the building based on the following formula specified byIBC2012:
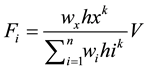 (10)
(10)
where, 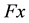 is the applied lateral force at level “x”, W is the story weight, h is the story height and V is the design base shear, and N is the number of stories. The summation in the denominator is carried through all story levels. This results in an inverted triangular distribution when k is set equal to unity. A uniform lateral load distribution consists of forces that are proportional to the story masses at each story level.
is the applied lateral force at level “x”, W is the story weight, h is the story height and V is the design base shear, and N is the number of stories. The summation in the denominator is carried through all story levels. This results in an inverted triangular distribution when k is set equal to unity. A uniform lateral load distribution consists of forces that are proportional to the story masses at each story level.
k = an exponent related to the structure period as follows:
For structures having a period of 0.5 sec or less, k = 1.
For structures having a period of 2.5 sec or more, k = 2.
2.1.2. Seismic Loads According to ESEE
Using the static lateral force procedure and according to the Regulations of the Egyptian Society for Earthquake Engineering (ESEE 1988) [14] every building shall be designed and constructed to withstand a total horizontal seismic force 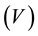 under consideration in accordance with the following formula: According to Clause 2.3.2.1 of the (ESEE) Regulations, the total horizontal seismic force V is given by:
under consideration in accordance with the following formula: According to Clause 2.3.2.1 of the (ESEE) Regulations, the total horizontal seismic force V is given by:
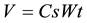
where:
Cs is the seismic design coefficient and shall be determined according to Clause 2.3.2.2 in the ESEE, Wt is the total weight. The seismic design coefficient Cs shall be determined from:

where:
Z is the seismic zoning factor.
I is the importance factor.
S is the structural system type factor (the value of S shall be determined separately for each direction).
M is the material factor.
R is the risk factor (where two values of R apply, the higher shall be used).
Q is the construction quality factor.
The seismic zoning factor (Z) shall be determined from:

In which:
A is a standard value of horizontal acceleration ratio and shall be determined in accordance with seismic zoning map shown in Figure 5 for The Sudan.
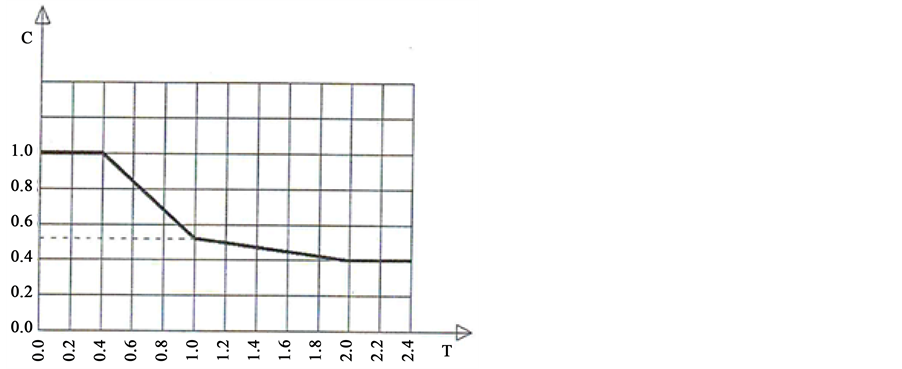
C is the coefficient of the standardized response spectrum for average damping of 5% as shown in Figure 1.
F is the foundation soil factor.
For buildings in which the total horizontal force is resisted by a moment resisting space frame the value of 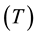
Figure 1. Coefficient of standardized response spectrum for average damping of 5% [14] .
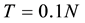
N is the total number of stories above the base.
Distribution of Horizontal Seismic Forces
For a regular building the total horizontal seismic force 
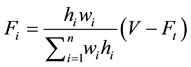
where:

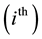
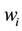





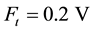
Where (H/d) is the height to width ratio of the building).
N is the total number of stories above the base of the building.
2.2. Seismic Map for The Sudan
In 2010, Sobaih and Hassaballa have developed new seismic maps for The Sudan, as shown in Figure 2 [15] .
Figure 2. Seismic hazard map of The Sudan [15] .
2.3. Description of the Buildings and Modeling
Four cases of existing RC buildings with 4, 6, 8 and 10 stories are considered for study as shown in Figure 3. The buildings are composed of moment resisting RC frames, situated in zone 3. The structure members are made of in-situ reinforced concrete. The main dimensions in plan are 20 meters in the × direction and 12 meters in the Y direction. The typical bay width and storey height of the four models are 4.0 and 3.0 meters, respectively and the ground floor height is 3.5 meters. Columns and beams sizes are shown in Table 1. The columns are assumed to be fixed at the base. The building is analyzed and designed as per seismic provisions provided by ESEE using BSI 8110 British Standard [16] and IBC2009 using ACI [17] . The general finite element package SAP 2000 (Version.14) [18] has been used for the analyses. A two-dimensional model of each structure has been created to undertake the nonlinear analysis. Beams and columns are modeled as nonlinear frame elements.

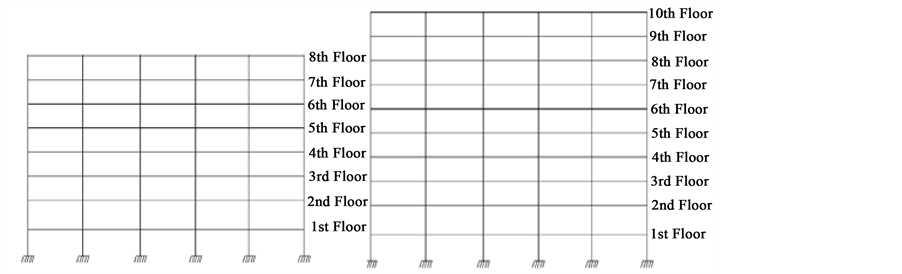
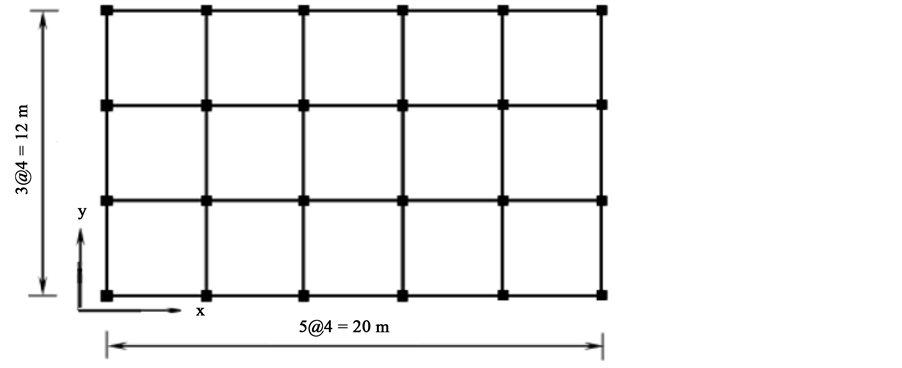
Figure 3. Dimensions of the studied buildings.
Table 1. Sections of columns and beams of the studied building.
SAP2000 provides default hinge properties and recommends M3 hinges for columns and M3 hinges for beams as described in FEMA 356 [19] .
2.4. Pushover Analysis
The static pushover analysis is becoming a popular tool for seismic performance evaluation of existing and new structures. The expectation is that the pushover analysis will provide adequate information on seismic demands imposed by the design ground motion on the structural system and its components. The pushover analysis of a structure is a static non-linear analysis under permanent vertical loads and gradually increasing lateral loads. The equivalent static lateral loads approximately represent earthquake induced forces.
2.4.1. Seismic Demand and Performance Point
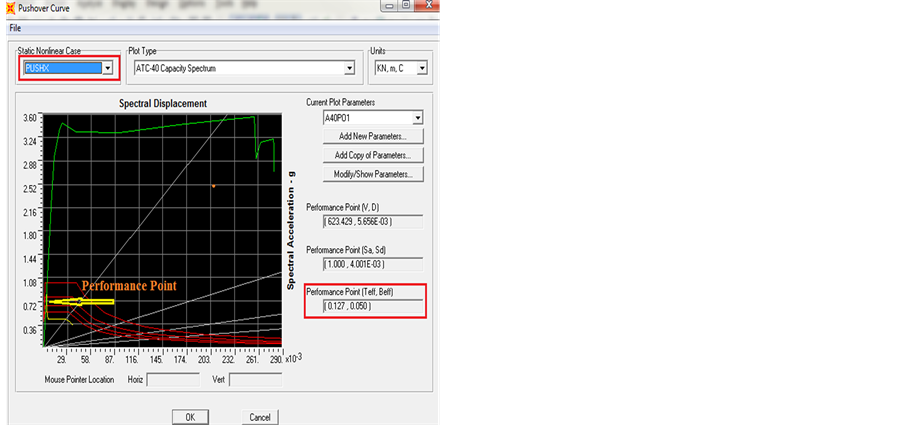
The performance point is the point where the capacity curve crosses the demand curve according to ATC-40 [20] . Two main approaches are used to evaluate the performance point (maximum inelastic displacement of the structure), Capacity-Spectrum Method of ATC-40 and Coefficient Method of FEMA 356.
In the present study, the Capacity-Spectrum Method is more suitable for the evaluation task. In the Capacity-Spectrum Method of ATC-40, the process begins with the generation of a force-deformation relationship for the structure. Then the results are plotted in Acceleration-Displacement Response Spectrum (ADRS) format. This format is a simple conversion of the base shear versus roof displacement relationship using the dynamic properties of the system, and the result is termed capacity spectrum for the structure. Figure 4 shows the determination of performance point.
According to ATC 40, the performance levels of buildings are as shown in Table 2.
2.4.2. Pushover Methodology
A pushover analysis is performed by subjecting a structure to a monotonically increasing pattern of lateral loads, representing the inertial forces which would be experienced by the structure when subjected to ground shaking. Under incrementally increasing loads various structural elements may yield sequentially. Consequently, at each event, the structure experiences a loss in stiffness. Using a pushover analysis, a characteristic nonlinear force displacement relationship can be determined. The main steps involved in pushover methodology are:
1) Definition of plastic hinges: In SAP2000, nonlinear behavior is assumed to occur within a structure at concentrated plastic hinges. The default types include an uncoupled moment hinges, an uncoupled axial hinges, an uncoupled shear hinges and a coupled axial force and biaxial bending moment hinges.
2) Definition of the control node: control node is the node used to monitor displacements of the structure. Its displacement versus the base-shear forms the capacity (pushover) curve of the structure.
Figure 4. Capacity and demand [21] .
Table 2. Performance level of building [19] .
3) Developing the pushover curve which includes the evaluation of the force distributions. To have a displacement similar or close to the actual displacement due to earthquake, it is important to consider a force displacement equivalent to the expected distribution of the inertial forces. Different forces distributions can be used to represent the earthquake load intensity.
4) Estimation of the displacement demand: This is a crucial step when using pushover analysis. The control is pushed to reach the demand displacement which represents the maximum expected displacement resulting from the earthquake intensity under consideration.
5) Evaluation of the performance level: Performance evaluation is the main objective of a performance based design. A component or action is considered satisfactory if it meets a prescribed performance.
The main output of a pushover analysis is in terms of response demand versus capacity. If the demand curve intersects the capacity envelope near the elastic range, Figure 5(a), then the structure has a good resistance. If the demand curve intersects the capacity curve with little reserve of strength and deformation capacity, Figure 5(b), then it can be concluded that the structure will behave poorly during the imposed seismic excitation and need to be retrofitted to avoid future major damage or collapse [22] .
3. Results and Discussion
This part presents the results of Analysis and Design of considered RC buildings. It also provides a through comparison between the IBC2012 code and the ESEE regulations so as to decide which code produces more vulnerable buildings. Figure 6 shows the label of columns
3.1. Beams Sections Design
The section properties resulting from using the IBC2012 and ESEE codes have the same cross-sections and reinforcement for beams. All beams are 500 × 300 with 8 Φ16 reinforcement.

Figure 5. (a) Safe design; (b) Unsafe design [22] .
Figure 6. Label of columns.
3.2. Columns Sections Design
Tables 3-10 show the cross-sections and reinforcing bars of members of the considered buildings according to IBC 2012 and ESEE codes.
3.3. Pushover Curves
The lateral capacity of the structures can be represented by a curve, which is plotted after applying the nonlinear static pushover analysis procedure. This curve is the relation between base shear which expresses the acting force on the structure, and roof displacement which expresses the lateral capacity of the structure. The pushover analysis using SAP2000 is achieved by using displacement control strategy for all RC frames.
The resulting pushover curves will be in terms of Base Shear?Roof Displacement (V-Δ). The slope of the pushover curves is gradually changed with increase of the lateral displacement of the building. This is due to the progressive formation of plastic hinges in beams and columns throughout the structure.
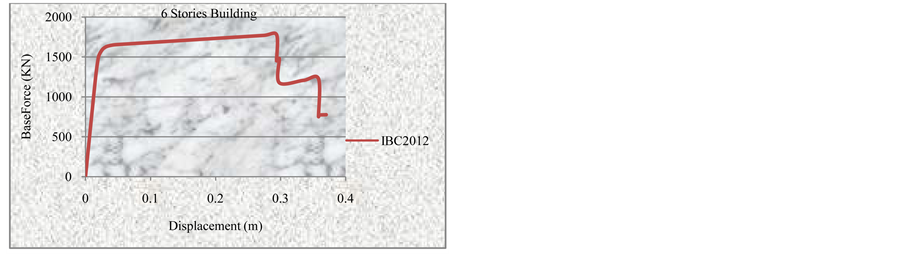
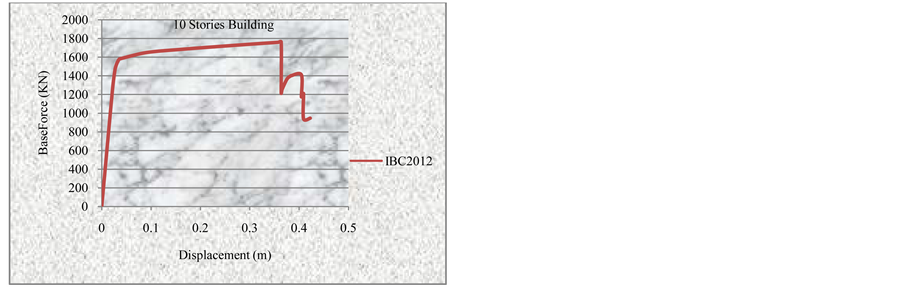
3.3.1. Pushover Curves Using IBC2012 Loads
The plastic deformation in the four buildings, i.e. the five points values, A-B-C-D-E, as shown in Figure 7, can be obtained after the SAP2000 analysis. The range AB is elastic range, B to IO is the range of immediate occupancy, IO to LS is the range of life safety and LS to CP is the range of collapse prevention. If all the hinges are within the CP limit then the structure is said to be safe. However, depending upon the importance of structure
Figure 7. Different stages of plastic hinges [23] [24] .
Table 3. Section properties in 4-stories building using ESEE code.
Table 4. Section properties in 4-stories building using IBC2012 code.
Table 5. Section properties in 6-stories building using ESEE code.
Table 6. Section properties in 6-stories building using IBC2012 code.
Table 7. Section properties in 8-stories building using ESEE code.
Table 8. Section properties in 8-stories building using IBC2012 code.
Table 9. Section properties in 10-stories building using ESEE code.
Table 10. Section properties in 10-stories building using IBC2012 code.
the hinges after IO range may also need to be retrofitted [23] . Figures 8-11 show the FEMA-356 pushover curves for the considered RC buildings heights 4, 6, 8 and 10 stories.
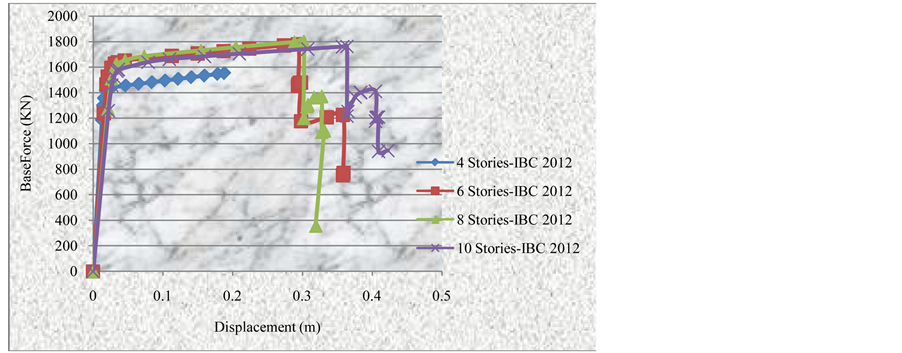
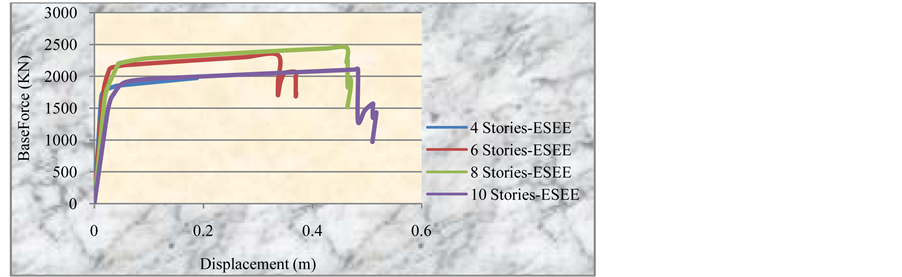
By combining the four curves in one graph to see the differences between each other, we can notice that the 10 storey building has the larger displacement on the curve as shown in Figure 12.
3.3.2. Pushover Curves Using ESEE Loads
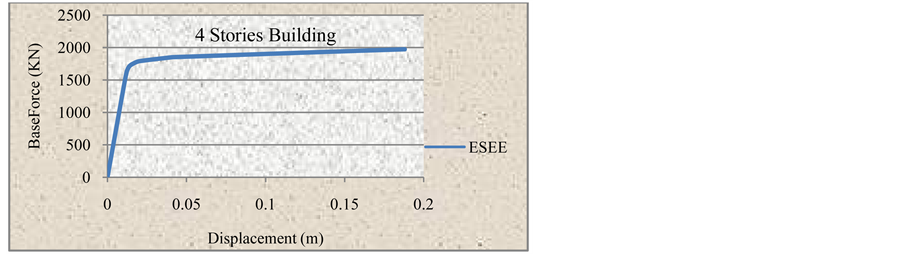
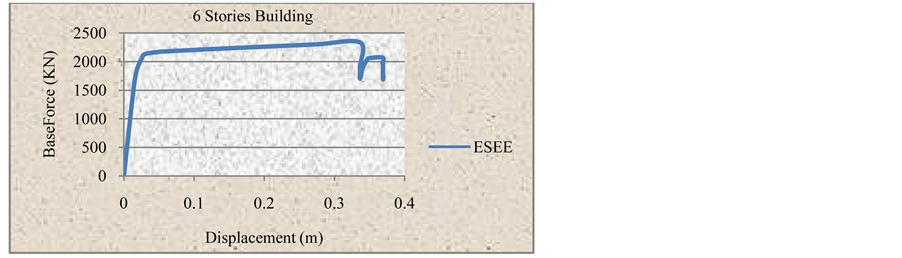
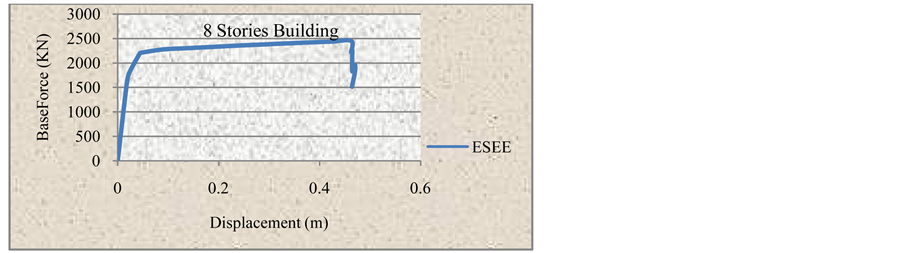
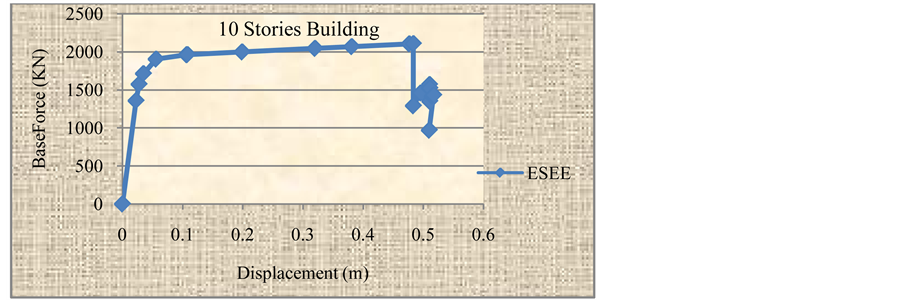
Similar to IBC2012 procedure, Figures 13-16 show the FEMA-356 pushover curves for the considered RC buildings heights 4, 6, 8 and 10 stories
By combining the four curves in one graph to see the differences between each other, we can notice that the 10 storey building has the larger base shear, displacement and consequently a larger target displacement on the curve as shown in Figure 17.
Figure 8. Pushover curve for 4-stories building using IBC2012.
Figure 9. Pushover curve for 6-stories building using IBC2012.
Figure 10. Pushover curve for 8-stories building using IBC2012.
Figure 11. Pushover curve for 10-storey building using IBC2012.
Figure 12. Combined pushover curve for the four buildings using IBC2012.
Figure 13. Pushover curve for 4-stories building using ESEE.
Figure 14. Pushover curve for 6-stories building using ESEE.
Figure 15. Pushover curve for 8-stories building using ESEE.
Figure 16. Pushover curve for 10-stories building using ESEE.
Figure 17. Combined pushover curve for the four buildings using ESEE.
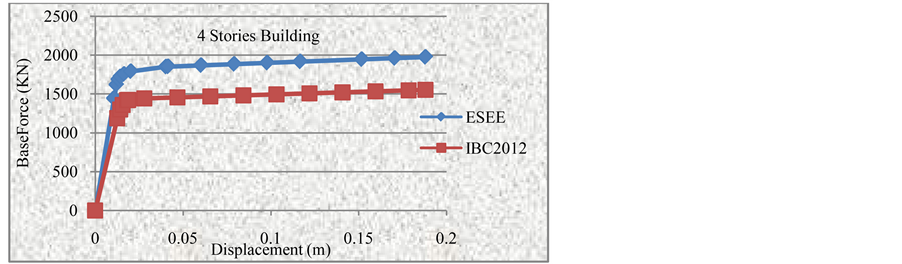
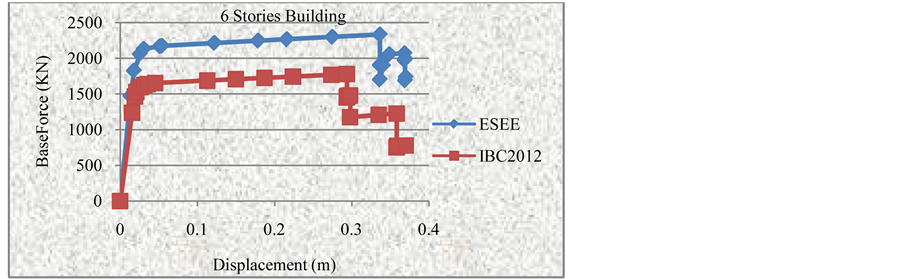
Figures 18-21 show the differences between each building using the IBC2012 code with its identical case using the ESEE regulations.
From the comparison of the 4-stories with its identical case in the ESEE regulations as shown in Figure 18, we can notice that there are obvious differences in values between the two codes. The ESEE regulations gives mush larger base shear, but they are similar to each other in terms of total displacement.
From the comparison of the 6-stories as shown in Figure 19, we find that the base shear gap between the two models is smaller comparing to 4-storey model. On the other hand, the ESEE loading code gives larger total displacement than the IBC2012 regulation.
From Figures 20, we can notice from the comparison of 8-Stories model that the ESEE gives higher base shear with much larger total displacement.
Moreover, from Figure 21, we find that the comparison of 10-stories model is similar to 6-stories model.
As a result, it is clear that the ESEE-designed buildings were stronger than the IBC2012 buildings, because as the loads increase there is a proportional increase in cross sections and reinforcement.
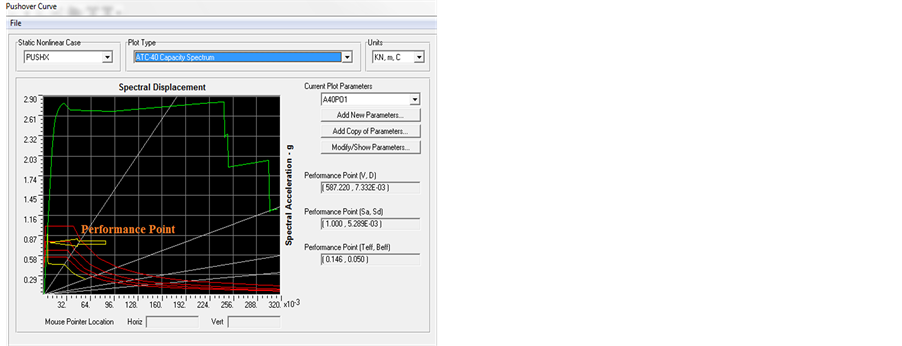
3.3.3. Performance Point According to ESEE
The resulting performance point for the four buildings are shown in Figure 22 and Figure 23 for 4, 6, 8 and 10 stories building, respectively. From the following figures, the performance point i.e. the point at which capacity curve and demand curve intersects is near to the event point B shown in Figure 7 in all the figures.
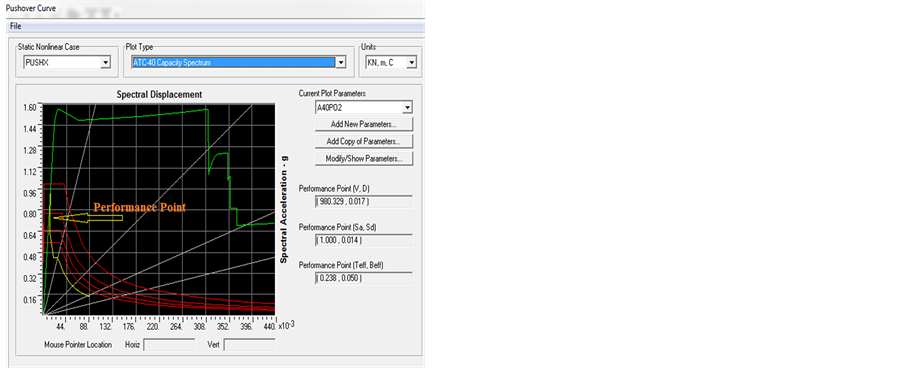
3.3.4. Performance Point According to IBC2012
Similarly, the IBC2012 demand-capacity curves for the four buildings are shown in Figure 24 and Figure 25 for 4, 6, 8 and 10 stories building, respectively.
3.3.5. Plastic Hinges Distribution Using IBC2012 Loads
Plastic hinge formation starts with beam ends and at top columns of lower stories, then consecutively to upper
Figure 18. Pushover curves for 4-stories building using IBC2012 and ESEE.
Figure 19. Pushover curves for 6-stories building using IBC2012 and ESEE.
Figure 20. Pushover curves for 8-stories building using IBC2012 and ESEE.
Figure 21. Pushover curves for 10-stories building using IBC2012 and ESEE.
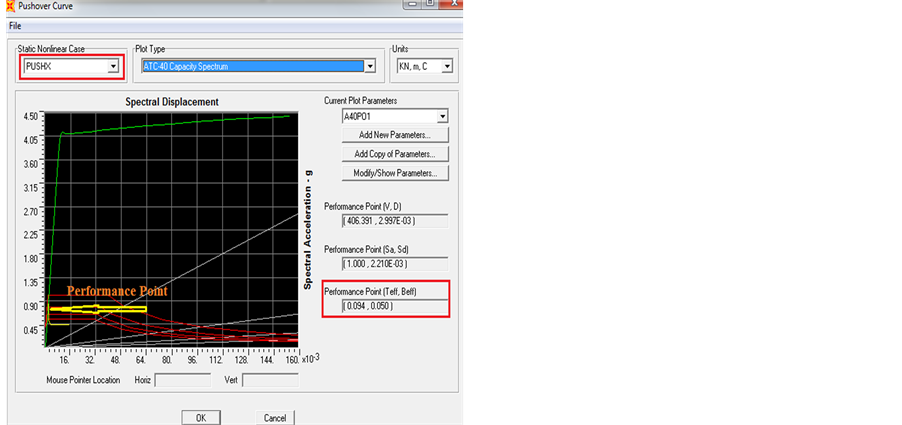
Figure 22. Performance point of 4 and 6 stories building using ESEE. (a) 4 Stories; (b) 6 Stories.

Figure 23. Performance point of 8 and 10 stories building using ESEE. (a) 8 Stories; (b) 10 Stories.

Figure 24. Performance point of 4 and 6 stories building using IBC2012. (a) 4 Stories; (b) 6 Stories.

Figure 25. Performance point of 8 and 10 stories building using IBC2012. (a) 8 Stories; (b) 10 Stories.
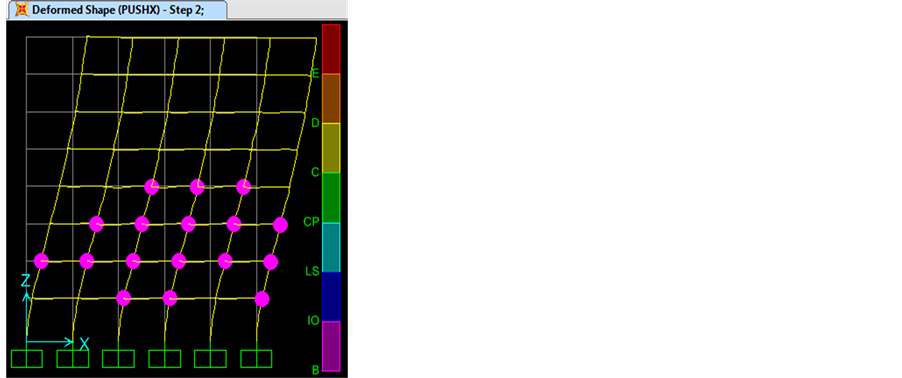
stories and continue with yielding of interior intermediate columns in the upper stories. But since yielding occurs at events B and IO respectively, the amount of damage in the two buildings will be limited. Figure 26 and Figure 27 show the plastic hinges distribution of considered RC buildings 4, 6, 8 and 10 stories.
For the 4-stories building, it was found that most of plastic hinges occurred in the columns, which do not satisfy the weak beam-strong column criteria. Moreover, these plastic hinges were located at the first and fourth levels.
From distribution of hinges for 6-stories building, it can be noticed that the plastic hinges were located at the second and third levels. Also, most of plastic hinges occurred in the beam column connections, which do not satisfy the weak beam -strong column criteria.
Finally, from distribution of hinges for 8-stories and 10-stories buildings, it can be noticed that the plastic hinges were located at the second, third and fourth levels. Also, most of plastic hinges occurred in the beam column connections, which do not satisfy the weak beam-strong column criteria.
3.3.6. Plastic Hinges Distribution Using ESEE Loads
Similarly, using the ESEE Loading code, Figure 28 and Figure 29 show that the plastic hinges distribution of the considered RC buildings 4, 6, 8 and 10 stories.
Similar to the IBC2012, it is found for the ESEE designed 4-stories building that most of plastic hinges occur in the beams, which satisfies the weak beam-strong column criteria.
From distribution of hinges for 6-stories, it can be noticed that the plastic hinges were located at the second, third and fourth floors. Also, most of plastic hinges occurred in the beams, which satisfy the weak beam-strong column criteria .These indicate that the ESEE building will sustain the earthquake loads longer than the IBC2012 code.
At last, from distribution of hinges for 8-stories and 10-stories buildings, it can be noticed that the plastic hinges were located at the third, fourth and fifth levels. Also, most of plastic hinges occurred in the beams, which satisfy the weak beam-strong column criteria.
4. Summary and Conclusions
Static pushover analysis is an attempt by the structural engineers to evaluate the real strength of the structure. This method of analysis promises to be a useful and effective tool for performance-based design of structure. Four existing RC buildings have been analyzed by this method and results have been compared in terms of base shear, displacement and plastic hinge pattern. From this study, the following conclusions can be drawn. The main concluding remarks are listed as follows:
1) Pushover analysis has been found relatively simple and evaluates the performance of the building close to more realistic behavior.

Figure 26. Distribution of hinges in 4 and 6 stories building using IBC2012. (a) 4 Stories; (b) 6 Stories.

Figure 27. Distribution of hinges in 8 and 10 stories building using IBC2012. (a) 10 Stories; (b) 8 Stories.
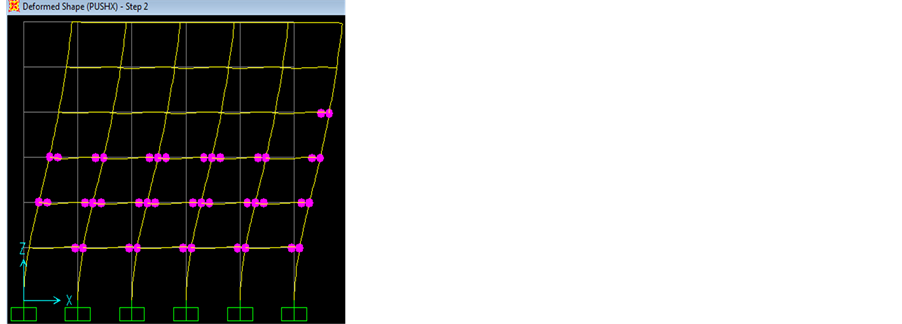
Figure 28. Distribution of hinges in 4 and 6 stories building using ESEE. (a) 4 Stories (b) 6 Stories.
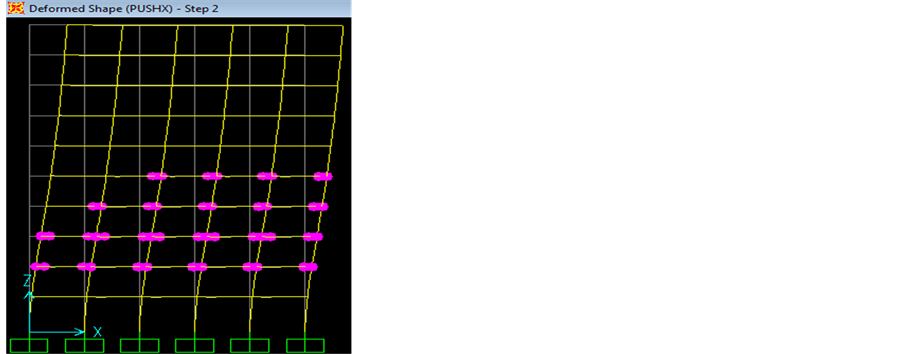
Figure 29. Distribution of hinges in 8 and 10 stories building using ESEE. (a) 8 Stories; (b) 10 Stories.
2) Pushover analysis can identify weak elements by predicting the failure mechanism and account for the redistribution of forces during progressive yielding. It may help engineers take action for rehabilitation work.
3) The results show that the design by ESEE and IBC 2012 are found adequate.
4) The buildings that are designed according to ESEE and IBC2012 are satisfactory. The performance point location is at IO (Immediate Occupancy) level. It means that the design satisfies pushover analysis according to ATC-40.
5) From distribution of hinges obtained from IBC2012 and ESEE, it can be noticed that most of plastic hinges obtained from ESEE occur in the beams, which satisfies the weak beam-strong column criteria. They indicate that the building which is designed by the ESEE code will sustain the earthquake loads longer than the IBC2012 code. Therefore, a structural engineer should consider the ESEE code in designing buildings in The Sudan.
6) From demand capacity curve according to IBC 2012 and ESEE, it is concluded that all the demand curves intersect the capacity curves near the event point B. Therefore, it can be concluded that the safety margin against collapse is high and there are sufficient strength and displacement reserves.
7) In all buildings, the demand curve intersects the capacity envelope near the elastic range, and then the structure has a good resistance.
References
- Abdalla, J., Mohamedzein, A., Yahia, E.A. and Abdelwahab, A. (1997) Seismic Hazard Assessment and Zoning of Sudan. Sudan Engineering Society Journal, 44, 35, 34-51.
- Martino, R., Spacone, E. and Kingsley, G. (2000) Nonlinear Pushover Analysis of RC Structures. Advanced Technology in Structural Engineering, 1-8. http://dx.doi.org/10.1061/40492(2000)38
- Giannopoulos, P.I. (2009) Seismic Assessment of RC Building According to FEMA 356 and Eurocode 8. Proceedings of the 16th Conference on Concrete, TEE, ETEK, 21-23 October 2009.
- Vijayakumar, D.L. (2012) Pushover Analysis of Existing Reinforced Concrete Framed Structures. European Journal of Scientific Research, 71, 195-202.
- Jitendra, N., Balaji, K.V. and Gopalaraju. S.S.V. (2012) Pushover Analysis of Unsymmetrical Framed Structures on Sloping Ground. International Journal of Civil, Structural, Environmental and Infrastructure Engineering Research and Development (IJCSEIERD), 2, 45-54.
- Golghate, K., Baradiya, V. and Sharma, A. (2013) Pushover Analysis of 4 Storey’s Reinforced Concrete Building. International Journal of Latest Trends in Engineering and Technology (IJLTET), 2, 80-84.
- Rahul, R., Limin, J. and Atila, Z. (2004) Pushover Analysis of a 19 Story Concrete Shear wall Building. Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, 1-6 August 2004, 133.
- Sobaih, M. and Ismaeil, M. (2012) A Proposed Methodology for Seismic Evaluation and Strengthening of Existing School Buildings in The Sudan. Proceedings of the 15th WCEE, Lisbon, 28-30 September, 2012, Paper No. 0571.
- Ismaeil, M.A., Hassaballa, A.E. and Sobaih, M. (2013) Assessment of Seismic Performance and Strengthening of RC Existing Residential Buildings in The Sudan. International Journal of Engineering Research & Technology (IJERT), 2, 442-450.
- Hassaballa, A.E. and Ismaeil, M.A. (2013) Seismic Retrofitting of a RC Building by Adding Steel Plate Shear Walls, IOSR Journal of Mechanical and Civil Engineering (JOSR-JMCE), 7, 49-62.
- Ismaeil, M.A. (2014) Pushover Analysis of Existing 3 Stories RC Flat Slab Building in The Sudan. Proceedings of the International Conference on Water, Energy, and Food Nexus for Sustainable Development, Pattaya, 19-21 November 2014, Paper No. 5092.
- Ismaeil, M., Hassaballa, A., Alzeadc, A. and Adamd, M. (2014) Pushover Analysis of Existing 4 Storey RC Flat Slab Building. International Journal of Sciences: Basic and Applied Research (IJSBAR), 16, 242-257.
- International Code Council (2012) International Building Code, IBC2012.
- ESEE (1988) Regulations for Earthquake-Resistance Design of Buildings in Egypt. Egyptian Society for Earthquake Engineering, Cairo.
- Sobaih, M. and Hassabala, A. (2010) Probabilistic Seismic Hazard Assessment for The Sudan. Proceedings of the 2nd European Conference on Earthquake Engineering and Seismology, Ohird, 12-17 October 2010, Paper No. 1332.
- BS 8110 (1997) The Structural Use of Concrete. British Standard Institution, London.
- ACI Committee 318 (2008) ACI 318-08 Building Code Requirements for Structural Concrete and Commentary. American Concrete Institute, Farmington Hills.
- CSI. SAP2000 V-14 (2010) Integrated Finite Element Analysis and Design of Structures Basic Analysis Reference Manual. Computers and Structures, Inc., Berkeley.
- FEMA-356 (2000) Prestandard and Commentary for Seismic Rehabilitation of Buildings. Federal Emergency Management Agency, Washington DC.
- (ATC) (1996) Seismic Evaluation and Retrofit of Concrete Buildings. Vol. 1 and 2, Report No. ATC-40, Applied Technology Council, Redwood City.
- Sofyan, A. (2013) Seismic Evaluation of Reinforced Concrete Frames Using Pushover Analysis. Al-Rafidain Engineering Journal, 21, 28-45.
- Hakim, R.A., Alama, M.S. and Ashour, S.A. (2014) Seismic Assessment of an RC Building Using Pushover Analysis, Engineering. Technology & Applied Science Research, 4, 631-635.
- Poluraju, P. and Nageswara Rao, P.V.S. (2011) Pushover Analysis of Reinforced Concrete Frame Structure Using SAP 2000. International Journal of Earth Sciences and Engineering, 4, 684-690.
- Maske, A.A., Nikhil, A.M. and Preeti, P.S. (2014) Pushover Analysis of Reinforced Concrete Frame Structures: A Case Study. International Journal of Advanced Technology in Engineering and Science, 2, 118-128.