Open Journal of Civil Engineering
Vol.05 No.01(2015), Article ID:53842,8 pages
10.4236/ojce.2015.51002
Anisotropic Damage Mechanics Modeling of Concrete under Biaxial Fatigue Loading
Ashkan Saboori1, Siamak Yazdani1, Denver Tolliver2
1Department of Civil and Environmental Engineering, North Dakota State University, Fargo, ND, USA
2Upper Great Plains Transportation Institute, North Dakota State University, Fargo, ND, USA
Email: ashkan.saboori@ndsu.edu, frank.yazdani@ndsu.edu, Denver.tolliver@ndsu.edu
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 15 January 2015; accepted 3 February 2015; published 6 February 2015
ABSTRACT
An anisotropic damage mechanics model is presented to describe the behavior and failure of concrete under biaxial fatigue loading. Utilizing the approach of bounding surfaces, the limit surface becomes a special case when the number of loading cycles is set to one. By increasing the number of loading cycles, the strength of concrete gradually decreases and the limit surface is allowed to contract and form new curves representing residual strengths. The magnitude of loading, load range, and the load path are known to influence the fatigue life and hence are addressed in this formulation. In this paper, a strength softening function is proposed in order to address the reduction in the strength of concrete due to fatigue. Separate softening functions are also proposed to account for the deformation characteristics in concrete under cyclic loading. Numerical simulations predicted by the model in both uniaxial and biaxial stress paths show a good correlation with the experimental data available in the literature.
Keywords:
Biaxial Fatigue, Bounding Surface, Concrete, Damage Mechanics, Stress-Strain

1. Introduction
The fatigue behavior of concrete has received a considerable attention among researchers in the past two de- cades. This can be attributed to the increasing use of concrete as a construction material. Concrete has been used in various structures due to its unique features such as high compressive strength, good resistance to aggressive and moist environments compare to some other construction materials, and enhancement in strength and deformation capacity under confining stresses. Concrete has been used in dams, bridges, and highway pavements in which cyclic loading is considered as one of the factors affecting its mechanical behavior during its service life. Various research studies have been published on the effects of fatigue loading on the mechanical behavior of concrete in terms of strength, deformation characterization, and modulus of elasticity. Most of these studies were conducted on the uniaxial loading of the material [1] -[10] , while only a few studies could be found in the literature on the effects of biaxial stress state loading [11] -[15] .
It is generally accepted that concrete under cyclic loading loses its strength gradually with an increase in the number of load cycles regardless of the loading path (uniaxial or biaxial). The strength loss during the fatigue process is due to nucleation and propagation of microcracks. During cyclic loading, these microcracks increase and grow to a stage in which major cracks are formed and reduce the load carrying area tremendously. At that point the strength of the material is decreased substantially and approaches the amplitude of the cyclic loading. This results in sudden rupture. It has been argued that at any given cycle, the fatigue strength of concrete under biaxial compression is greater than that under uniaxial compression [12] [14] . This is the result of the relative confinement provided in the biaxial loading state. This confinement restricts the nucleation and propagation of microcracks by applying load in two perpendicular directions.
In addition to the strength reduction, fatigue loading affects the modulus of elasticity and the deformational capacity of concrete as well. Awad [4] and Gao and Hsu [1] have investigated the effects of fatigue loading on the ultimate strain of concrete (strain at which failure occurs) and have concluded that the strain increases under cyclic loading state compared to monotonic state. Awad [4] has shown that the ultimate and the irreversible plastic strains accumulated after each cycle prior to failure, depend on the number of cycles that have been applied. In addition to the maximum stress, it has also been shown that stress range has significant effects on the fatigue life of concrete [2] [8] . By keeping the maximum stress unchanged and decreasing the stress range, the number of cycles to failure will increase. These results, have also been investigated and validated by Awad [4] .
According to Gao and Hsu [1] the fatigue strain of concrete is comprised of three parts: irreversible strain caused by cyclic creep under the action of average stresses; irreversible strain caused by fatigue cracks; and fatigue strain range. In the same study [1] , it was reported that the modulus of elasticity of concrete degrades during fatigue process due to damage accumulation which happens as a result of microcracking.
Realizing the fact that fatigue loading has a significant influence on concrete serviceability and may lead to an abrupt material failure, an accurate and efficient model which could capture the behavior of concrete is needed.
In this paper, an approach based on continuum damage mechanics is proposed to model the behavior of concrete under fatigue loading. The general theory of bounding surface approach proposed by Wen et al. [16] is utilized here in order to capture the strength reduction in concrete due to cyclic loading. In the bounding surface approach, the limit surface is allowed to contract to form smaller surfaces, called residual strength surfaces, as the fatigue loading is applied. A softening function for the loss of strength based on the maximum stress, stress range, and load path is proposed. These features are considered a significant improvement and extension to the work reported by Wen et al. [16] . To capture the effects of fatigue on deformational characterization and material stiffness, two additional softening functions have been proposed to predict the ultimate and plastic strains in the last cycle of loading under any arbitrary fatigue loading. These additional features of the formulation are considered novel enhancing the predictive capability of the model. At the end, results are compared with experimental data showing a good correlation.
2. General Formulation
The general formulation shown in the following is based on the damage mechanics approach and follows the framework of the internal variable theory of thermodynamics. For isothermal and small deformations, the Gibbs Free Energy is obtained as follows [17] [18] :
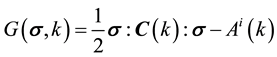 (1)
(1)
where C is the compliance tensor, 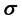 is the stress tensor, k is a scalar damage parameter, and
is the stress tensor, k is a scalar damage parameter, and 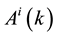 is a scalar function associated with the surface energy of microcracks. The symbol “:” represents a tensor contraction operation. A constitutive relation for concrete like materials is used as:
is a scalar function associated with the surface energy of microcracks. The symbol “:” represents a tensor contraction operation. A constitutive relation for concrete like materials is used as:
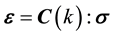 (2)
(2)
where ε represents strain tensor. The compliance tensor, C, is assumed to take an additive decomposition form as:
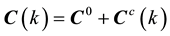 (3)
(3)
where C0 and Cc are the initial undamaged compliance tensor of the material and the added flexibility tensor associated with the accumulation of damage, respectively. Due to the nonlinearity behavior between stress and strain for brittle materials, the rate form of the flexibility tensor must be considered as:
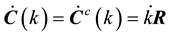 (4)
(4)
In Equation (4), the response tensor, R, determines the direction at which damage occurs. For isothermal and small deformation, the internal dissipation inequality can be represented by Gibbs Free Energy as:
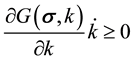 (5)
(5)
It is also assumed that the damage is an irreversible phenomenon in which,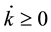 . By combining Equations (1) through (5), the general form of the damage surface is given by:
. By combining Equations (1) through (5), the general form of the damage surface is given by:
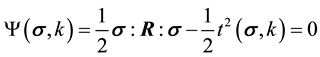 (6)
(6)
where  is called the damage function. The condition
is called the damage function. The condition 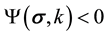 describes the elastic condition for the material which is enclosed by the damage surface
describes the elastic condition for the material which is enclosed by the damage surface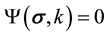 . The condition
. The condition 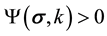 is not allowed for rate-independent processes.
is not allowed for rate-independent processes.
Guided by the experimental data [17] , the following form for the damage function is postulated as:
 (7)
(7)
where fc is the compressive strength of concrete, E0 is the initial stiffness, and “e” represents the natural number. In this paper only the compression mode of damage is considered. Guided by work of Wen et al. [9] and Saboori et al. [19] , the damage mode is identified by the response tensor R given as:
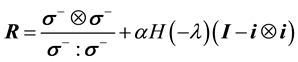 (8)
(8)
where “⊗” is the tensor product operator, 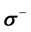 represents the negative cone of the stress tensor,
represents the negative cone of the stress tensor, 


3. Bounding Surface Approach
The bounding surface approach for fatigue was proposed by Wen et al. [16] in order to predict the behavior of woven fabric composites under fatigue loading. This surface is shown schematically in Figure 1. In the case of fatigue loading, as cyclic loading is applied, the limit surface is allowed to contract and to form residual strength curves. This reduction in strength is caused by damage and microcracks generated during the fatigue process. As the number of load cycles increases, the strength continues to decrease further and the residual surfaces also shrink. The reduction in strength continues to a point at which the residual strength becomes equal to the magnitude of loading. At this point, failure surface is formed and the material cannot withstand any additional cycles resulting in failure.
In order to capture the described behavior of concrete under cyclic loading, an evolutionary equation is needed to predict the failure surface. To accomplish this task, the damage function is restructured to be the product of two functions as shown below:

where 
Figure 1. Schematic representation of bounding surfaces in biaxial stress space.
function, 
By considering a fatigue uniaxial compression path and substituting Equation (9) into Equation (6), the following form is obtained for the softening function:

where σ is the residual strength of the concrete after specific number of cyclic loading. Equation (10) is a representation of so-called S-n curves. Based on the researches reported in [2] [8] [20] , amplitude of loading, σmax; stress ratio, r; and finally the load path all contribute to the fatigue life of concrete. While the fatigue life of concrete is adversely affected by the amplitude of loading, Aas-Jakobsen and Lenschow [2] reported that increasing stress ratio results in a greater fatigue life at a given stress. Moreover, considering the data provided by Yin and Hsu [13] , it is apparent that the rate of reduction in concrete strength is not the same for different load paths. Guided by these findings, the following softening function is proposed in this paper as:

where n is the number of cyclic loading and A and B are material parameters. Utilizing this softening function and incorporating it into the Equation (6), residual strength surfaces could be obtained under various load paths. The inclusion of the first and second invariants of the stress tensor allows the formulation to model load path dependency observed in fatigue testing.
In Figure 2, a schematic representation of stress-strain behavior of concrete which is consistent with the experimental data [4] is illustrated. The applied stress is signified as σmax and the fatigue failure strain in uniaxial compression is given by
To fully describe the stress-strain behavior of concrete under fatigue loading, four factors including reduction in strength, increase in ultimate strain, plastic strain after each cycle, and reduction in modulus of elasticity need to be addressed. The reduction in strength has been already addressed by the strength softening function; Equation (11). For deformation, as was discussed earlier, concrete under fatigue loading fails at an ultimate strain greater than the one under monotonic loading state. Awad [4] reported that by increasing the stress ratio, both ultimate and plastic strain increases and therefore results in a more flexible concrete. Awad [4] also showed that amplitude of loading adversely affects both ultimate and residual strains. In order to capture such effects on the mechanical characteristics of concrete two strain softening functions are presented as follows:
Figure 2. Schematic representation of stress-strain of concrete under monotonic and cyclic loading.


where 



4. Numerical Example
In this section, results predicted by the model are compared with the experimental data obtained from literature. Material parameters α, A, B, β, and γ are calculated based on the experimental data presented.
Figure 3 shows the prediction results of residual strength surfaces in biaxial stress space against experimental data work of Nelson et al. [11] . The damage surfaces show a good correlation for monotonic loading when n = 1 as well as for fatigue loading when n = 10, 100, and 1000 with experimental data. For Figure 3, following material parameters are used: α = 0.587, A = ‒0.0445, and B = 1.521.
Figures 4-6 show the strength versus number of loading cycles for concrete under cyclic uniaxial and biaxial paths with stress ratios of 0.5 and 1.0. These figures show that the strength of concrete materials would decrease with increase in the number of cycles, n. The rate of strength reduction for these three figures are different, meaning that the strength loss is also dependent on the load path. This is consistent with the experimental data and is captured by the proposed model. For Figures 4-6, the following material parameters are used: α = 0.745, A = ‒0.0431, and B = 0.552.
Figure 7 illustrates the comparison between the experimental data provided by Awad [4] and S-n curves obtained by the model for three uniaxial fatigue loading with different stress ratios. As shown, this model captures the effect of stress range on fatigue life of concrete. It can be seen that for any constant stress amplitude, the model predicts a greater fatigue life for a stress range of 0.65 - 0.68 than a stress range of 0.41 - 0.47 and 0
Figure 3. Residual strength surfaces for various number of cyclic loading, experimental data by Neslon et al. [11] .
Figure 4. S-n curve for concrete under uniaxial cyclic loading, experimental data by Yin and Hsu [13] .
Figure 5. S-n curve for concrete under biaxial cyclic loading with stress ratio 0.5, experimental data byYin and Hsu [13] .
which is in consistent with the experimental data in the literature. For the following figures, the material parameters used are: α = 0.94, A = ‒0.0263, β = 0.0787, and γ = 0.1241.
Figure 8 and Figure 9 represent the capability of the model in predicting the ultimate strain and residual strain of concrete under uniaxial fatigue loading after different cycles of loading. The model predicts higher ran- ge of ultimate and residual strain for fatigue loading with lower amplitude. This is in conformity with the discussion that was presented earlier and implies that concrete becomes more flexible under fatigue loading with lower amplitude. Also, Figure 9 shows the increase in residual strain by increasing the stress range. That is, for a given “n”, the residual strain increases with increasing stress range.
Figure 10 and Figure 11 show the stress-strain curves of concrete under uniaxial monotonic and fatigue
Figure 6. S-n curve for concrete under biaxial cyclic loading with stress ratio 1.0, experimental data by Yin and Hsu [13] .
Figure 7. S-n curves for concrete under uniaxial loading with various stress ranges, experimental data by Awad [4] .
Figure 8. Ultimate strain versus number of cycles for concrete under uniaxial cyclic loading, experimental data by Awad [4] .
loading with amplitudes of 0.95fc and 0.9fc. The reduction in strength and longitudinal modulus and increase in ultimate strain are predicted by the model. It can also be noticed that the ultimate and residual strain predicted by the model for fatigue loading with 0.9fc amplitude is greater than the ones for 0.95fc that follows the arguments discussed earlier in the paper. Not all of the cycles to failure are shown in Figure 11 for clarity.
5. Conclusion
An anisotropic model is utilized to predict the strength behavior of concrete under biaxial compressive fatigue
Figure 9. Plastic strain versus loading cycles under uniaxial cyclic loading with various stress ranges, experimental data by Awad [4] .
Figure 10. Stress-strain curves under cyclic (σmax/fc = 0.95) and monotonic uniaxial loading, experimental data by Awad [4] .
Figure 11. Stress-strain curves under cyclic (σmax/fc = 0.9) and monotonic uniaxial loading, experimental data by Awad [4] .
loading. Under cyclic fatigue loading, the limit surface is allowed to contract and form new surfaces identified as residual strength surface. This is accomplished by proposing a softening function that is based on amplitude, stress ratio, and load path. By including these parameters, the effects of strange range and the load paths on the fatigue life of concrete are studied and predicted. Furthermore, to capture the effects of fatigue loading on stress-strain behavior of concrete, two additional strain softening functions are proposed for changes in ultimate and residual (plastic) strains. The influencing factors on ultimate and plastic strains such as amplitude, load path, and load range are incorporated into the proposed softening functions. At the end, the results obtained from the model are compared with the experimental data in the literature showing a good comparison.
Acknowledgements
This research was supported by a grant from US DOT to the Department of Civil and Environmental Engineering at North Dakota State University through MPS program. The authors would like to thank US DOT for the financial support for conducting this research.
References
- Gao, L. and Hsu, C.-T.T. (1998) Fatigue of Concrete Under Uniaxial Compression Cyclic Loading. ACI Materials Journal, 95, 578-581.
- Aas-Jakobsen, K. and Lenschow, R. (1973) Behavior of Reinforced Columns Subjected to Fatigue Loading. ACI Journal Proceedings, 70, 199-206.
- Petkovic, G., Lenschow, R., Stemland, H. and Rosseland, S. (1990) Fatigue of High-Strength Concrete. ACI Special Publication, 121, 505-526.
- Awad, M.E. (1971) Strength and Deformation Characteristics of Plain Concrete Subjected to High Repeated and Sustained Loads. University of Illinois Engineering Experiment Station, College of Engineering, University of Illinois, Urbana-Champaign.
- Holmen, J.O. (1982) Fatigue of Concrete by Constant and Variable Amplitude Loading. ACI Special Publication, 75, 71-110.
- Zhang, B., Phillips, D. and Wu, K. (1996) Effects of Loading Frequency and Stress Reversal on Fatigue Life of Plain Concrete. Magazine of Concrete Research, 48, 361-375. http://dx.doi.org/10.1680/macr.1996.48.177.361
- Hordijk, D. and Reinhardt, H. (1993) Numerical and Experimental Investigation into the Fatigue Behavior of Plain Concrete. Experimental Mechanics, 33, 278-285. http://dx.doi.org/10.1007/BF02322142
- Hsu, T.T. (1981) Fatigue of Plain Concrete. ACI Journal Proceedings, 78, 292-305.
- Kim, J.-K. and Kim, Y.-Y. (1996) Experimental Study of the Fatigue Behavior of High Strength Concrete. Cement and Concrete Research, 26, 1513-1523. http://dx.doi.org/10.1016/0008-8846(96)00151-2
- Paskova, T. and Meyer, C. (1997) Low-Cycle Fatigue of Plain and Fiber-Reinforced Concrete. ACI Materials Journal, 94, 273-286.
- Nelson, E.L., Carrasquillo, R.L. and Fowler, D.W. (1988) Behavior and Failure of High-Strength Concrete Subjected to Biaxial-Cyclic Compression Loading. ACI Materials Journal, 85, 248-253.
- Su, E.C. and Hsu, T.T. (1988) Biaxial Compression Datigue and the Discontinuity of Concrete. ACI Materials Journal, 85, 178-188.
- Yin, W. and Hsu, T.C. (1995) Fatigue Behavior of Steel Fiber Reinforced Concrete in Uniaxial and Biaxial Compression. ACI Materials Journal, 92, 71-81.
- Lu, P.Y., Li, Q.B. and Song, Y.P. (2007) Behavior of Concrete under Nonproportional Biaxial Fatigue Stresses with One Constant. ACI Materials Journal, 104, 3.
- Buyukozturk, O. and Tseng, T.-M. (1984) Concrete in Biaxial Cyclic Compression. Journal of Structural Engineering, 110, 461-476. http://dx.doi.org/10.1061/(ASCE)0733-9445(1984)110:3(461)
- Wen, C., Yazdani, S., Kim, Y.J. and Abdulrahman, M. (2012) Bounding Surface Approach to the Modeling of Anisotropic Fatigue Damage in Woven Fabric Composites. Open Journal of Composite Materials, 2, 125-132. http://dx.doi.org/10.4236/ojcm.2012.24015
- Ortiz, M. (1985) A Constitutive Theory for the Inelastic Behavior of Concrete. Mechanics of Materials, 4, 67-93. http://dx.doi.org/10.1016/0167-6636(85)90007-9
- Yazdani, S. (1993) On a Class of Continuum Damage Mechanics Theories. International Journal of Damage Mechanics, 2, 162-176. http://dx.doi.org/10.1177/105678959300200204
- Saboori, A., Yazdani, S., Reberg, A. and Tolliver, D. (2014) Anisotropic Damage Modeling of Concrete Subjected to Freeze-Thaw Process. International Journal of Civil & Structural Engineering, 5, 42-52.
- Qiao, P. and Yang, M. (2006) Fatigue Life Prediction of Pultruded E-Glass/Polyurethane Composites. Journal of Composite Materials, 40, 815-837. http://dx.doi.org/10.1177/0021998305055549












