Modern Mechanical Engineering
Vol.07 No.01(2017), Article ID:73935,19 pages
10.4236/mme.2017.71002

Coherent Application of a Contact Structure to Formulate Classical Non-Equilibrium Thermodynamics

Edwin Knobbe1, Dirk Roekaerts2

1Department of Research Battery Technology, BMW Group, Munich, Germany

2Department Process and Energy, Delft University of Technology, Delft, The Netherlands

Copyright © 2017 by authors and Scientific Research Publishing Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

Received: September 21, 2016; Accepted: February 3, 2017; Published: February 6, 2017

ABSTRACT

This contribution presents an outline of a new mathematical formulation for Classical Non-Equilibrium Thermodynamics (CNET) based on a contact structure in differential geometry. First a non-equilibrium state space is introduced as the third key element besides the first and second law of thermodynamics. This state space provides the mathematical structure to generalize the Gibbs fundamental relation to non-equilibrium thermodynamics. A unique formulation for the second law of thermodynamics is postulated and it showed how the complying concept for non-equilibrium entropy is retrieved. The foundation of this formulation is a physical quantity, which is in non- equilibrium thermodynamics nowhere equal to zero. This is another perspective compared to the inequality, which is used in most other formulations in the literature. Based on this mathematical framework, it is proven that the thermodynamic potential is defined by the Gibbs free energy. The set of conjugated coordinates in the mathematical structure for the Gibbs fundamental relation will be identified for single component, closed systems. Only in the final section of this contribution will the equilibrium constraint be introduced and applied to obtain some familiar formulations for classical (equilibrium) thermodynamics.

Keywords:

Non-Equilibrium Thermodynamics, Gibbs Fundamental Relation, Contact Geometry, Second Law of Thermodynamics, Equilibrium Constraint

1. Introduction

The main objective of this paper is to derive a mathematical framework for macroscopic non-equilibrium thermodynamics, which is not based on some kind of an (implicit) equilibrium assumption. Instead it will be shown, that the equilibrium conditions are “contained” in the proposed framework by applying an additional constraint. There are two key components in this innovative derivation: 1) a generalization of Gibbs fundamental relation for non-equilibrium thermodynamics that is based on the dissipation of energy and 2) a unique formulation of the second law of thermodynamics, including a mathematical proper derivation of non-equilibrium entropy as a thermodynamic state function. This paper presents the mathematical framework of Classical Non-Equilibrium Thermodynamics (CNET) based on a harmonious integration of mathematics and physics.

In his monumental work “On the Equilibrium of Heterogeneous Substances” [1] Josiah Willard Gibbs (1839-1903) postulates a relation that is fundamental for thermodynamics, viz.

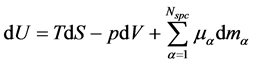. (1)

Gibbs postulates this relation for a mixture of 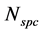non-reacting, chemical species in a closed system, which is in a thermodynamic equilibrium state. Often this relation is derived by a simple elimination of the reversible heat flow from both laws of thermodynamics [2] - [7] or it is applied in non-equilibrium states by using the local equilibrium hypothesis [8] . In this paper, only a state space for non-equilibrium thermodynamics will be postulated and the corresponding generalization of the fundamental relation will be derived. This paper will be restricted to closed, single component systems, but a proposition to include the physical phenomena of open systems with chemical reactions can be found in [9] .

Based on the original work of Rudolf Clausius (1822-1888), the macroscopic entropy of systems in thermodynamic equilibrium is often defined as the quotient of heat flow and temperature. For non-equilibrium processes this definition is then simply extended to an inequality (e.g. Clausius inequality [6] ) or an additional term is included in the definition of macroscopic entropy [10] . The major drawback of these approaches is, that it is not obvious that entropy is also a state function in non-equilibrium thermodynamics. It is often reasoned, that the non-equilibrium entropy has to be a thermodynamic state function. This paper presents a unique postulate for the second law of thermodynamics, which does not explicitly include the concept of entropy. Based on a mathematical property of this postulate, the non-equilibrium entropy will be derived with the appropriate mathematical structure of a thermodynamic state function. This paper is confined to the thermodynamic state space, there is no reference to temporal or spatial coordinates.

Section 2 starts with the introduction of a thermodynamic state and defines a corresponding state function. The mathematical machinery of contact geometry is used to postulate the so-called non-equilibrium state space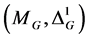. Darboux’s theorem can be derived for a contact structure, which possesses the mathematical structure of the Gibbs fundamental relation in thermodynamics (viz. Equation (1)). In the third section the first law of thermodynamics is postulated in such a way, that the internal energy is a state function that complies with the appropriate definition. The next step is to postulate a unique formulation for the second law of thermodynamics and the complying derivation of non-equili- brium entropy. Both sections are combined in Section 4 to identify the thermodynamic potential as Gibbs free energy and to identify the pairs of conjugated coordinates in Darboux’s theorem. With this identification, a generalized Gibbs fundamental relation for non-equilibrium thermodynamics is derived, which includes sufficient additional degrees of freedom to model non-equilibrium phenomena. The postulate for a thermodynamic equilibrium is postponed until the final section of this paper. It will be shown how the equilibrium constraint reduces Gibbs fundamental relation to a Pfaffian equation, which is the basis for the derivation of the so-called Maxwell relations in thermodynamics [3] [5] [6] [7] .

2. Non-Equilibrium State Space

A powerful feature of phenomenological thermodynamics is its capability to make statements about the macroscopic state of a system without detailed knowledge of its microscopic details. This feature is based on the phenomenological observation, that a finite number of macroscopic properties is required to completely describe the thermodynamics of a system. Non-equilibrium thermodynamics will be described in a separate state space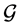, which is based on statistical averages of the phase space in statistical mechanics.

A thermodynamic system consists of 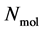molecules, where each individual molecule 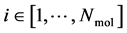has a position 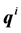and a momentum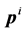. The complete set of these 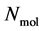positions and 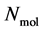momenta form the so-called microscopic state of the system. The number of degrees of freedom in this system is, in the case of a 3-dimensional spatial space, equal to 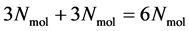(where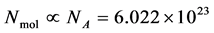). A macroscopic state is a statistical ensemble of this huge amount of microscopic information, where there is a probability distribution over all compatible microscopic states of the system. The corresponding probability density 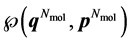determines the probability that the system will be found in the infinitesimal phase space volume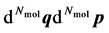. It complies with

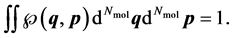(2)

Then the statistical average of some physical observable 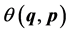can be written as (e.g. see [11] [12] [13] [14] )

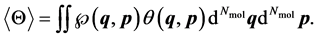(3)

This equation defines a macroscopic property of a system, which will be applied as a coordinate for the differential manifold of the thermodynamic state space. At this point, no clear mathematical distinction will be made between the definition of the chart, as part of the definition of the manifold, and the set of values of the macroscopic properties, which form together the thermodynamic state. Typical examples for macroscopic properties are energy, volume, number of molecules or electric charge. A set of coordinates builds a macroscopic non-equilibrium state, viz.. Notice that there is no explicit expression for time nor for spatial distributions of macroscopic properties within the system.

Non-equilibrium thermodynamics describes changes in a system, which depend on changes in its state due to some arbitrary process. There are various macroscopic properties of the system that depend on the state, which requires the definition of a so-called state function.

Definition 1 [Non-equilibrium state function]. The 0-form, that is generated by an exact 1-form, is defined as a non-equilibrium state function. Hence,

(4)

In this definition symbol denotes an exterior derivative with respect to the thermodynamic coordinates, which makes it an essential part of the definition. It describes the dependencies of the thermodynamic changes, which are given by the set of independent macroscopic properties of the system (again, there is no reference to temporal or spatial coordinates). Another important aspect of the above definition is that any non-equilibrium property can return to its initial condition after an arbitrary periodic process has concluded a complete period1.

The manifold is not sufficient to completely describe non-equilibrium thermodynamics. By using the mathematical framework of contact geometry, the thermodynamic space can be based on the concept of a contact structure. In 1973 Robert Hermann [15] suggested to formulate equilibrium thermodynamics based on a -dimensional differential manifold and a non-de- generating contact 1-form. In this paper his mathematical framework will be used as the basic building block to formulate non-equilibrium thermodynamics.

Postulate 1 [Gibbs state space]. Non-equilibrium thermodynamics is specified by a -dimensional differential manifold, that is equipped with a non-degenerate Gibbs contact 1-form, viz.

(5)

The Gibbs state space is defined by the contact structure.

In the general context of this paper, it is very important to notice, that this postulate is neither the first law nor the second law of thermodynamics. The above postulate states that the contact structure formulates a non-equilibrium thermodynamic state space. In this paper, all thermodynamic observations will be formulated in this state space. The non-degenerate Gibbs contact 1-form has two important mathematical properties (see [16] [17] ):

・ it is never equal to zero, so it is either everywhere positive or it is everywhere negative,

・ it is not completely integrable (Frobenius condition).

Both these properties play a key role in the formulation of the second law of thermodynamics in section 3. The physical interpretation of the quantity is postponed until the next section.

According to Darboux’s theorem (see [16] [17] [18] [19] [20] ), there is a set of canonical coordinates on the manifold such that the Gibbs contact 1-form is specified by

(6)

(summation over repeated indices). This equation can be identified as a generalization of the Gibbs fundamental relation, e.g. see Equation (1). Thus, the mathematical structure of the Gibbs fundamental relation is not postulated in this paper. Instead it is derived from a mathematical property of the contact structure that defines the non-equilibrium thermodynamic state space. It is also not derived from the combination of both laws of thermodynamics, so it is a third essential component in the mathematical formulation of non-equili- brium thermodynamics. The canonical coordinate will be called a thermodynamic potential, hence

Definition 2 [Thermodynamic potential]. The canonical coordinate, whose change is directly proportional to the Gibbs contact 1-form, is defined as the thermodynamic potential, viz..

Symbols and in Equation (6) denote the conjugated coordinates, since they form conjugated pairs of extensive and intensive quantities, or vice versa. The number of degrees of freedom in the Gibbs state space is determined by the dimensions of the manifold, i.e.. At this point it must be emphasized that, and are coordinates in the Gibbs state space that defines non-equilibrium thermodynamics. Equation (6) from Darboux’s theorem specifies only the functional relation between these non-equilibrium coordinates and captures the complete mathematical wealth of irreversible, non-equilibrium thermodynamics. One of the remaining issues will be to identify the physical meaning of the thermodynamic potential and the set of canonical coordinates and. But before these coordinates can be identified, it is required to introduce the first and second law of thermodynamics.

3. Thermodynamic Laws

The distinction between exact and inexact 1-forms is an essential part of the mathematical formulation of the first and second laws of thermodynamics. The first law of thermodynamics states that for an arbitrary periodic process, the energy at the start and end of a complete period are identical. This statement complies with the definition of a non-equilibrium state function (e.g. see Definition 1). Both the amount of heat flow and work flow are each path dependent quantities (viz. both are inexact 1-forms), so they are not conserved over a complete period in a periodic process. The first law of thermodynamics states that their sum is conserved.

Postulate 2 [First law of thermodynamics]. Summation of the inexact 1-forms for heat flow and work flow results in an exact 1-form, viz.

(7)

The crucial feature in the above postulate is, that the sum of two inexact 1-forms and results in an exact 1-form. According to Definition 1 there exists then a non-equilibrium state function, which will be called internal energy, such that

(8)

The internal energy is conserved over a complete period of an arbitrary periodic process due to the definition of the exterior derivative (viz., which is equivalent with the cycle integral).

In nature, it is observed that, for closed systems, processes are such that the system eventually approximates an equilibrium state. Once a system has obtained such an equilibrium state, interactions with the surroundings of the system are required to disturb this equilibrium. Hence, processes are directed towards a mathematical extremum, which corresponds with the equilibrium state, and this is irreversible when there is no interference from outside the system. Observations of these phenomena are for the first time published by Sadi Carnot (1796-1832, see [4] [21] ) and later mathematically formulated by Rudolf Clausius (see [22] [23] ). Clausius postulates, that a system in an equilibrium state has a macroscopic property, which he calls entropy and is mathematically defined by2

(9)

As is already stated before, the heat flow is a path dependent quantity and thus an inexact 1-form (viz.). Frobenius integration theorem (see type 2) in Table 1 or [18] [24] [25] [26] ) is used in Clausius formulation to transform the inexact 1-form to the exact 1-form. From a mathematical perspective, the quantity is called an integrating factor, which is a different mathematical mechanism to obtain an exact 1-form compared to the one that is used

Table 1. Overview of the Frobenius integrability condition (e.g. see [18] [24] [25] ).

in Postulate 2. In classical thermodynamics, the above definition is then often extended to non-equilibrium states by replacing the equal sign with an unequal sign or by adding some other term3. In such an approach, it is not clear that entropy is a non-equilibrium state function in thermodynamics, since it is not properly derived as an exact 1-form. This lack of mathematical accuracy might be one of the reasons why there are so many formulations of non-equilibrium thermodynamics.

(10)

In these relations denotes the uncompensated heat in analogy to the “uncompensirten Verwandlung” in the work of Clausius [23] . The last relation with can only be found in his paper [28] , where his Equation (8) has the same structure as Equation (13) in this paper. Opposite to this paper, is not identified as an integrating factor for the term and the quantity itself is not specified in further detail.

One of the less famous pioneers in thermodynamics is the Greek mathematician Constantin Carathéodory (1800-1900). His work [30] [32] [33] on the use of Pfaffian equations for the mathematical formulation of thermodynamics has been crucified4, although it is one of the first attempts for a rigorous formalization of thermodynamics. In the second axiom in his 1909 paper [31] , he has an interesting formulation for the second law of thermodynamics that is based on geometrical considerations:

Axiom II: In jeder beliebigen Umgebung eines willkürlich vorgeschriebenen Anfangszustandes gibt es Zustände, die durch adiabatische Zustandsänderungen nicht beliebig approximiert werden können5.

Above axiom is in the literature also known as Carathéodory’s inaccessibility condition or as Carathéodory’s principle [30] . Notice that Carathéodory makes a statement about an arbitrary initial state, so in this axiom there is no explicit restriction to a thermodynamic equilibrium. But in his paper an adiabatic process is defined as a process where the systems remain in (phase) equilibrium when the deformable coordinates change6. So the heat transfer is not necessarily always equal to zero, which is in the textbook of Bamberg and Sternberg [13] [24] elegantly formulated by the mathematical concept of a null curve, viz.

(11)

Based on the Frobenius integration theorem the second relation is derived from Axiom II and therefore also known as Carathéodory’s theorem [24] [35] [36] .

So modern interpretations of mathematical formulations for the definition of entropy in classical thermodynamics show, that the Frobenius integration theorem plays a crucial role. But opposite to the before mentioned formulations, in this paper Frobenius integration theorem is not applied to the inexact 1-form for heat flow. As is shown in both before mentioned cases, this would explicitly or implicitly require that there is an equilibrium state. Recall that the Gibbs contact 1-form is explicitly postulated to be non-degenerate, so it is not integrable by itself. Therefore, and this is a unique feature of the mathematical formulation in this paper, Frobenius integration theorem is applied to the difference between the heat flow and dissipation, viz..

Postulate 3 [Second law of thermodynamics]. The difference between the inexact 1-form for heat flow and the non-degenerating Gibbs contact 1-form that represents the dissipation is completely integrable, viz.

(12)

Similar to the approach of Carathéodory, the concept of entropy is not defined in the above formulation for the second law of thermodynamics. Based on the integrability condition in Postulate 3 it can then be shown (see [18] [37] ), that there exists exactly one pair of conjugated coordinates. Here these coordinates are denoted by the absolute temperature and non-equilibrium entropy, such that

(13)

The exterior derivative of entropy is an exact 1-form due to the presence of the integrating factor in the right-hand side of Equation (13). Hence, the existence of entropy as a non-equilibrium state function is based on a different mathematical mechanism compared to internal energy in the first law of thermodynamics. It is emphasized that both internal energy and entropy are introduced in this paper as non-equilibrium state functions. Finally, notice that both the absolute temperature and the Gibbs contact 1-form are nowhere equal to zero, so they are either everywhere positive or everywhere negative. Hence, in this paper the second law is not dominated by an inequality, but by the observation that certain physical quantities cannot be equal to zero.

An integral part of the definition of a non-equilibrium state function is, that the initial value is identical to the final value at the end of a complete period in a periodic process. This means that the initial and final non-equilibrium state must be identical and consequently this has to hold for every macroscopic property. As is already mentioned in Section 2, the likelihood that the statistically averaged value of every macroscopic property is recovered after a complete period in a real physical system is very small. But it is not equal to zero and thus it has to be considered as a limiting case in non-equilibrium thermodynamics. Consider Equation (13) for the case of a complete period, then

(14)

Both the absolute temperature and the dissipation are never equal to zero, hence their quotient is unequal to zero. This means that the right-hand side in the last relation is always either positive or negative. Consequently, the heat flow in a periodic process must have the same direction over every completed period and thus a heat flow is required to drive a periodic process. Or conversely, in non-equilibrium thermodynamics there does not exist a process that is both periodic and adiabatic at the same time. This is an intriguing observation, since Clausius’s formulation for entropy is based on periodic processes, while Carathéodory uses adiabatic processes to specify the second law of thermodynamics.

4. Identification of Thermodynamic Coordinates

In this section the thermodynamic potential and the pairs of conjugated coordinates and in Equation (6) will be identified for the case of a single component, closed system (e.g. there is no mass transfer with the surrounding of the system). The basic elements for this identification are both laws of thermodynamics, but first the work flow has to be specified in more detail. In general, every 1-form can be written as a linear combination of the corresponding coordinates. The coordinates for work are force and displacement, thus the inexact 1-form for the work flow can be written as

(15)

This equation does not add new information to the presented mathematical framework of non-equilibrium thermodynamics. It only specifies the set of coordinates that determines the work flow. Symbols and (with) denote respectively generalized thermodynamic forces and displacements7, where blackboard fonts are used to denote extensive quantities. The indices are and for the general case, but for a single component, closed system it will be shown that. Combine above equation with Equations (8) and (13), then the following equation can be obtained

(16)

By comparing this equation with Equation (6), one could argue that the thermodynamic potential and the set of conjugated coordinates are identified. But this identification would not be a sound mathematical proof due to the presence of the contact 1-form. Furthermore, this reasoning obscures another important thermodynamic quantity, which is already hidden in the three proposed postulates.

Opposite to most textbooks on thermodynamics, in this paper the definition of the Gibbs free energy is not one of the building blocks for the mathematical formulation of thermodynamics. Instead the Gibbs free energy is derived from the combination of the three proposed postulates in non-equilibrium thermodynamics and the above general specification for the work flow.

Theorem 1 [Gibbs free energy]. For a single component, closed system the thermodynamic potential in the generalized fundamental relation (e.g. Equation (6)) is the so-called Gibbs free energy, viz.

(17)

The corresponding pairs of conjugated coordinates and are:

(18)

Proof. The proof starts with the combination of the generalized Gibbs fundamental relation and the second law of thermodynamics by substituting Equation (13) into Equation (6). Then replace the 1-form for heat flow using the first law of thermodynamics. Finally, use the above specification of the work flow to obtain

(19)

Notice that due to these steps the Gibbs contact 1-form is removed from the above equation, so the Gibbs fundamental relation is reduced to a Pfaffian equation where. This is the essential step that provides crucial features for the following derivation.

The next step in this proof is based on a unique property of thermodynamic properties: thermodynamic properties are either extensive or intensive quantities. Extensive quantities are proportional to the size (or extend) of the thermodynamic system and therefore scalable, while intensive quantities are independent of the size of the system. The total volume of the system is used here to scale every extensive quantity in Equation (19), hence

(20)

Consider the case that all conjugate coordinates denoted by are extensive quantities (viz. then) and all conjugated coordinates denoted by are intensive quantities8. Substitute every relation in Equation (20) to the corresponding terms in Equation (19) and apply the product rule of differentiation. Rearrange the resulting equation by collecting all terms with either or to obtain

(21)

The total volume of a thermodynamic system is larger than zero, while the change of volume can be positive, negative or equal to zero. So, for an arbitrary system, above equation can only hold when both terms between the brackets are equal to zero. Hence, the following two relations have been derived

(22)

and

(23)

Equation (23)2 is obtained by multiplying Equation (23)1 with the total volume. The thermodynamic potential, as it is specified in Equation (23), is called the Gibbs free energy and is therefore denoted by symbol.

The final step in this proof is to identify the set of conjugated coordinates and. Apply therefore the exterior derivative to Equation (23)2 with and use again the product rule of differentiation, then

(24)

This is again a Pfaffian equation for a thermodynamic state function, either for the Gibbs energy or the internal energy. Subtract then Equation (19) from the above Pfaffian equation, which results in the following relation

(25)

There are conjugated pairs of intensive and extensive quantities in the above equation, of which the intensive quantities must be identified. Thermodynamic state variables can change independently and in the Gibbs state space there are exactly conjugate pairs of intensive and extensive quantities (see Darboux’s theorem on page 5). Hence, the set of specified intensive quantities must be identical to the set that must be identified in this proof. Apply this insight to above equation and rearrange to get

(26)

Again, for an arbitrary thermodynamic process the above equation can only hold when all terms between brackets are equal to zero. The set of extensive conjugated coordinates is therefore also determined.

Equation (17), which is in this paper derived in the above proof, is in the literature also known as Euler’s relation (e.g. see [38] [39] [40] ). Substitute Equation (17) and the pairs of conjugated coordinates in Theorem 1 into Equation (6) to obtain the following generalized formulation for the Gibbs fundamental relation

(27)

Equation (16) can be derived by subtracting the above equation from Equation (27), where. The equation can also be derived by repeating the proof of Theorem 1 for the reversed case, where every is an intensive quantity and every is an extensive quantity (viz. then). This case shows that the thermodynamic potential is specified by the following Euler equation

(28)

Both Equations (16) and (27) are implementations of Equation (6) for single component, closed systems, which is therefore a generic formulation of the third key element of thermodynamics (besides both laws of thermodynamics). Both equations confirm that Gibbs free energy and internal energy are thermodynamic potentials according to Definition 2. Finally, notice that both equations contain identical 1-forms, viz. and the Gibbs contact 1-form.

5. Equilibrium Constraint

So far, this paper has been focused on the general case of non-equilibrium states and arbitrary irreversible processes. For an isolated system (then there are no interactions with the surroundings), it is in nature observed, that the macro- scopic state of the system does not change any more if one waits sufficiently long. The corresponding thermodynamic state is called the equilibrium state of the system for which the change of a state function is equal to zero, hence

(29)

Molecules do not stop moving in such an equilibrium state; there are many fluctuations of the microstates, which are not visible on the macroscopic level. On a macroscopic level, any perturbation away of an equilibrium state requires some kind of exchange with the surrounding of the system. The above equation implements a mathematical extremum, which is not present in the proposed mathematical framework for non-equilibrium thermodynamics due to the mathematical properties of the Gibbs contact 1-form. 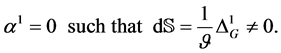To further clarify this point, consider Equation (13) for the case of a closed system without any heat flow, then

(30)

The absolute temperature and the Gibbs contact 1-form are defined to be everywhere unequal to zero. So, in the case of non-equilibrium thermodynamics, the change of entropy cannot be equal to zero, as is required for an equilibrium state.

Based on the above considerations it becomes clear, that an additional mathematical construct is required to embed equilibrium thermodynamics within the proposed mathematical framework. Consider therefore an arbitrary irreversible process and some other kind of process. Equilibrium thermodynamics is then formulated by the Legendre submanifold, which is induced by the pull-back of a map applied to the Gibbs contact 1-form [16] [41] [42] [43] .

Postulate 4 [Equilibrium constraint]. There exists an equilibrium map

, who’s pull-back is governed by the equilibrium constraint

(31)

This postulate can also be found in the original work of Hermann [15] and Mrugała [44] on thermodynamics in a geometric framework. The modern literature (e.g. see [15] [16] [43] [44] [45] [46] ) uses the Legendre manifold to derive classical relations in equilibrium thermodynamics. For instance, Mrugała writes9: A Legendre manifold of is a maximum dimensional integral manifold of the Pfaffian equation. Classical formulations follow the approach of Carathéodory, which is based on Pfaffian equations and exact 1-forms (e.g. see [18] [30] [31] [33] ).

The distinction between the equilibrium Legendre state space and the non-equilibrium Gibbs state space can be clarified based on the visualization in Figure 1. The figure shows two equilibrium hypersurfaces denoted by and, which are both a function of the coordinates and. There are indefinitely many equilibrium hypersurfaces, but some of them have at one equilibrium state identical partial derivatives (e.g. see point in the figure). A thermodynamic process is reversible if it connects only equilibrium states that are on the same equilibrium hypersurface (viz. the solid lines denoted by and). A process becomes irreversible when two neighboring equilibrium states do not belong to the same equilibrium hypersurface. The transition between two equilibrium hypersurfaces requires that the thermodynamic system has been in a non-equilibrium state. For instance, the non-equilibrium states which connect the equilibrium states and (here shown as a jump by the dotted line). Notice that these non-equilibrium states depend, besides and, also on the corresponding conjugated coordinates and.

Next some results will be obtained for the case of equilibrium thermodynamics. An underline will be used in this paper to denote symbols that refer to an

Figure 1. Geometric visualization of the Legendre state space for equilibrium thermodynamics. The graph contains two equilibrium hypersurfaces denoted by and. The solid lines and show two reversible processes, including their projection on the -plane (dotted lines between and). Any process that leaves an equilibrium hypersurface is irreversible, hence the cycle that goes through the points can not be reversed without any interaction with the surroundings.

equilibrium state on the Legendre submanifold. Apply first the pull-back of the equilibrium map to the change of the thermodynamic potential in Equation (6), then

(32)

Then a similar procedure can be applied to pairs of conjugated coordinates in Equation (6), where the 1-form becomes equal to

(33)

Thus, application of the equilibrium map in Postulate 4 to the generalized Gibbs fundamental relation in Equation (6) results in

(34)

The last relation is called a Pfaffian equation, where the 1-form is an exact 1-form (see also Definition 1). A state function is in general a 0-form, where the evaluation of the exterior derivative is straightforward (e.g. see [17] [25] [47] ). Select the set with as coordinates, then

(35)

The relations in Equation (35)3 follow from the combination of Equations (34)2 and (35)2, so these relations are only valid for equilibrium thermodynamics. To further clarify this point, consider internal energy as it is defined in Postulate 2 by the exact 1-form. Evaluate Equation (35)2 for the non-equili- brium case10 and combine the result with Equation (16) to obtain

(36)

Since the Gibbs contact 1-form is everywhere unequal to zero, it is not possible to derive relations from the terms between brackets. This observation confirms that the relations in Equation (35)3 do not hold for non-equilibrium thermodynamics.

Another example of interesting formulations in equilibrium thermodynamics are the so-called Maxwell relations (e.g. see [3] [7] [48] ). Apply the equilibrium constraint in Postulate 4 to Equation (16), which reduces to the following Pfaffian equation on the Legendre submanifold

(37)

The second relation shows the correct set of canonical coordinates to completely specify internal energy in the case of equilibrium thermodynamics. Apply this knowledge to Equation (35)2 and substitute the result in the above Pfaffian equation to obtain

(38)

Mixed derivatives that originate from a closed 1-form are symmetric11. So, differentiate the first relation with respect to volume and the second relation with respect to entropy, which results in

(41)

(39)

Based on the Poincaré lemma, it can be proven that every exact 1-form is also a closed 1-form (see [17] [25] ). Hence is a closed 1-form, which means that its exterior derivative is equal to zero. Apply the exterior derivative to the case of the above example, which results in

(40)

The term between parentheses has to vanish since. Equation (35)2 shows that the coefficients and are equal to the partial derivatives of the generating function, which results in the mixed partial derivatives (See also [16] ).

This is one of the familiar four Maxwell relations [3] [5] [6] [7] [48] , where it is shown in this paper that they can be derived only for the case of equilibrium thermodynamics. Finally, apply the pull-back of map to Equation (27) to obtain the following Gibbs fundamental relation on the Legendre submanifold

(42)

So, the thermodynamic potential (viz. here) is a state function according to Definition 1 in the case of equilibrium thermodynamics. Notice that Equation (6) is not a Pfaffian equation due to the presence of the Gibbs contact 1-form, which is everywhere unequal to zero. Consequently the 1-form in Equation (6) is neither an exact nor a closed 1-form. The thermodynamic potential is in the presented mathematical framework for non-equilibrium thermodynamics not explicitly postulated as a state function that complies with Definition 1.

6. Conclusions

Classical Non-Equilibrium Thermodynamics (CNET) is the science of phenomenological changes in the state of systems. Especially these changes make the tools of differential geometry extremely suited for a rigorous mathematical formulation. The presented formulation for non-equilibrium thermodynamics consists of the following three base postulates:

・ there exists a non-equilibrium thermodynamic phase space (Gibbs state space),

・ energy is conserved (first law of thermodynamics),

・ the difference between heat flow and dissipation is completely integrable (second law of thermodynamics).

The thermodynamic phase space is built upon macroscopic properties of a system. Neither temporal nor spatial coordinates are considered in the presented mathematical formulation of non-equilibrium thermodynamics. The direction of processes is not implemented by an explicit inequality in the second law of thermodynamics. Instead an implicit reverse is applied: there is a physical quantity that is nowhere equal to zero, viz. the dissipation of energy. Furthermore, no explicit signs are assigned to nowhere vanishing physical quantities. Still this formulation shows clearly that there can only be a periodic process if and only if it is driven by the appropriate heat flow.

Together with the definition of a state function, other relations are derived based on the mathematical properties of this formulation. The mathematical structure for the Gibbs fundamental relation follows from the Gibbs state space. Through a clever combination with both laws of thermodynamics it can be proven that the thermodynamic potential is specified by the Gibbs free energy. Other coordinates in the formulation of the Gibbs fundamental relation are identified for a single component, closed system. Notice that there is neither in the postulates, nor in the derivation of the mathematical framework for non- equilibrium thermodynamics any assumption that restricts the arbitrary processes to certain classes (e.g. periodic, adiabatic, sufficiently slow, etc.).

The introduction of an equilibrium state is postponed until the final section, where it is introduced as an extremum (viz. no change of a state function). This is mathematically implemented by the pull-back of an equilibrium map with the condition that there is no dissipation of energy. Such an elaborate construction is required, because the dissipation of energy is in the general case of non- equilibrium thermodynamics by definition unequal to zero. For the case of an equilibrium state, the Gibbs fundamental relation reduces to a Pfaffian equation. It is shown that the Maxwell relations in thermodynamics can be derived only for the case of an equilibrium state.

Cite this paper

Knobbe, E. and Roekaerts, D. (2017) Coherent Application of a Contact Structure to Formulate Classical Non-Equilibrium Thermodynamics. Modern Mechanical Engineering, 7, 8-26. https://doi.org/10.4236/mme.2017.71002

References

  1. 1. Gibbs, J.W. (1928) On the Equilibrium of Heterogeneous Substances. In: Collected Works, Volume I: Thermodynamics, Chapter III, Longmans, Green, New York, 55-353. (Originally published in Transactions of the Connecticut Academy, III, pp. 108-248, 1876, and pp. 343-524, 1878).

  2. 2. Haupt, P. (2002) Continuum Mechanics and Theory of Materials. 2nd Edition, Springer, Berlin.
    https://doi.org/10.1007/978-3-662-04775-0

  3. 3. Moran, M.J. and Shapiro, H.N. (1998) Fundamentals of Engineering Thermodynamics. 3rd Edition, John Wiley & Sons, Chichester.

  4. 4. Müller, I. (2007) A History of Thermodynamics: The Doctrine of Energy and Entropy. Springer-Verlag, Berlin.

  5. 5. Nickel, U. (2011) Lehrbuchder Thermodynamik: Einverstandliche Einfuhrung. 2. Auflage Edition, PhysChemVerlag, Erlangen. (In German)

  6. 6. Nolting, W. (2012) Grundkurs Theoretische Physik 4: Spezielle Relativitatstheorie, Thermodynamik. 8. Auflage Edition, Springer-Verlag, Berlin. (In German)

  7. 7. Smith, J.M., Van Ness, H.C. and Abbott, M.M. (2005) Introduction to Chemical Engineering Thermodynamics. 7th International Edition, McGraw-Hill Chemical Engineering Series. McGraw-Hill, Boston.

  8. 8. Kjelstrup, S. and Bedeaux, D. (2008) Non-Equilibrium Thermodynamics of Heterogeneous Systems. Series on Advances in Statistical Mechanics (Vol. 16), World Scientific Publishing Co. Pte. Ltd, Singapore.
    https://doi.org/10.1142/6672

  9. 9. Knobbe, E.M. (2010) On the Integration of the Arbitrary Lagrangian-Eulerian Concept and Non-Equilibrium Thermodynamics. PhD Thesis, Delft University of Technology, Delft.

  10. 10. Kondepudi, D. and Prigogine, I. (1998) Modern Thermodynamics: From Heat Engine to Dissipative Structure. John Wiley & Sons, Chicester.

  11. 11. Attard, P. (2012) Non-Equilibrium Thermodynamics and Statistical Mechanics: Foundations and Applications. Oxford University Press, Oxford.
    https://doi.org/10.1093/acprof:oso/9780199662760.001.0001

  12. 12. Olla, P. (2015) An Introduction to Thermodynamics and Statistical Physics. UNITEXT for Physics. Springer International Publishing, Cham.
    https://doi.org/10.1007/978-3-319-06188-7

  13. 13. Scheck, F. (2008) Theoretische Physik: Statistische Theorie der Warmeleitungstheorie. Springer-Verlag, Berlin. (In German)

  14. 14. Zorich, V. (2011) Mathematical Analysis of Problems in the Natural Sciences. Springer-Verlag, Berlin.
    https://doi.org/10.1007/978-3-642-14813-2

  15. 15. Hermann, R. (1973) Geometry, Physics, and Systems. Pure and Applied Mathematics. Marcel Dekker, Inc., New York.

  16. 16. Arnol’d, V.I. (1989) Mathematical Methods of Classical Mechanics. Vol. 60, 2nd Edition, Springer-Verlag, New York.
    https://doi.org/10.1007/978-1-4757-2063-1

  17. 17. McInerney, A. (2013) First Steps in Differential Geometry: Riemannian, Contact, Symplectic. Undergraduate Texts in Mathematics. Springer Science + Business, Media.

  18. 18. Edelen, D.G.B. (1985) Applied Exterior Calculus. John Wiley & Sons, Inc., New York.

  19. 19. Kushner, A., Lychagin, V. and Rubtsov, V. (2007) Contact Geometry and Nonlinear Differential Equations. Volume 101 of Encyclopedia of Mathematics and It’s Applications, Cambridge University Press, Cambridge.

  20. 20. Lang, S. (2002) Introduction to Differentiable Manifolds. Universitext. 2nd Edition, Springer, New York.

  21. 21. Mendoza (1988) Reflections on the Motive Power of Fire. Dover Publications, Inc., Mineola.

  22. 22. Clausius, R.J.E. (1854) Uebereineveranderte Form des zweitenHauptsatzes der mechanischen Warmetheorie. Annalen der Physik und Chemie, 169, 481-506. (In German)

  23. 23. Clausius, R.J.E. (1865) Ueberverschiedenefür die Anwendungenbequeme Formen der Hauptgleichungen der mechanischen Warmetheorie. Poggendorff’s Annalen der Physik, 125, 353-400. (In German)

  24. 24. Bamberg, P.G. and Sternberg, S. (1990) A Course in Mathematics for Students of Physics. Volume 2, Cambridge University Press, Cambridge.

  25. 25. Frankel, T. (2004) The Geometry of Physics: An Introduction. 2nd Edition, Cambridge University Press, Cambridge.

  26. 26. Szekeres, P. (2004) A Course in Modern Mathematical Physics: Groups, Hilbert Space and Differential Geometry. Cambridge University Press, Cambridge.
    https://doi.org/10.1017/CBO9780511607066

  27. 27. Eu, B.C. (1995) Form of Uncompensated Heat Giving Rise to a Pfaffan Differential Form in Thermodynamic Space. Physical Review E, 51, 768-771.

  28. 28. Eu, B.C. (1999) Generalized Thermodynamics of Global Irreversible Processes in a Finite Macroscopic System. Journal of Physical Chemistry B, 103, 8583-8594.

  29. 29. Eu, B.C. (2004) Generalized Hydrodynamics in the Transient Regime and Irreversible Thermodynamics. Philosophical Transactions of the Royal Society A, 362, 1553-1565.
    https://doi.org/10.1098/rsta.2004.1404

  30. 30. Born, M. (1921) Kritische Betrachtungen zur traditionellen Darstellung der Thermodynamik. Physikzeitschrift, 22, 218-224, 249-254, 282-286. (In German)

  31. 31. Carathéodory, C. (1909) Untersuchungenüber die Grundlagen der Thermodynamik. Mathematische Annalen, 67, 355-386. (In German)
    https://doi.org/10.1007/BF01450409

  32. 32. Caratheodory, C. (1925) Uber die Bestimmung der Energie und der absoluten Temperature mitHilfe von reversible Prozessen. Sitzungsberichte der Praußischen Akademie der Wissenschaftenzum, Berlin, 39-47. (In German)

  33. 33. Pogliani, L. and Berberan-Santos, M.N. (2000) Constantin Carathéodory and the Axiomatic Thermodynamics. Journal of Mathematical Chemistry, 28, 313-324.

  34. 34. Truesdell, C. (1984) Rational Thermodynamics. 2nd Edition, Springer, New York.
    https://doi.org/10.1007/978-1-4612-5206-1

  35. 35. Uffink, J. (2001) Bluff Your Way in the Second Law of Thermodynamics. Studies in History and Philosophy of Modern Physics, 32B, 305-394.
    https://doi.org/10.1016/S1355-2198(01)00016-8

  36. 36. Uffink, J. (2003) Entropy, Chapter 7: Irreversibility and the Second Law of Thermodynamics. Princeton Series in Applied Mathematics, Princeton University Press, Princeton, 121-146.

  37. 37. Salamon, P., Andresen, B., Nulton, J.D. and Konopka, A.K. (2006) Systems Biology: Principles, Methods and Concepts, Chapter 9: The Mathematical Structure of Thermodynamics. CRC Press, Boca Raton, 207-221.

  38. 38. Lebon, G., Jou, D. and Casas-V’azquez, J. (2008) Understanding Non-Equilibrium Thermodynamics: Foundations, Applications, Frontiers. Springer-Verlag, Berlin.
    https://doi.org/10.1007/978-3-540-74252-4

  39. 39. Reichl, L.E. (2009) A Modern Course in Statistical Physics. 3rd Revised and Updated Edition, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim.

  40. 40. Shell, M.S. (2015) Thermodynamics and Statistical Mechanics: An Integrated Approach. Cambridge University Press, Santa Barbara.
    https://doi.org/10.1017/CBO9781139028875

  41. 41. Haslach Jr., H.W. (1997) Geometric Structure of the Non-Equilibrium Thermodynamics of Homogeneous Systems. Reports on Mathematical Physics, 39, 147-162.

  42. 42. Mrugala, R. (1993) Continuous Contact Transformations in Thermodynamics. Reports on Mathematical Physics, 33, 149-154.
    https://doi.org/10.1016/0034-4877(93)90050-O

  43. 43. Mrugala, R., Nulton, J.D., Schon, J.C. and Salamon, P. (1991) Contact Structure in Thermodynamic Theory. Reports on Mathematical Physics, 29, 109-121.

  44. 44. Mrugala, R. (1978) Geometrical Formulation of Equilibrium Phenomenological Thermodynamics. Reports on Mathematical Physics, 14, 419-427.
    https://doi.org/10.1016/0034-4877(78)90010-1

  45. 45. Mrugala, R. (1985) Submanifold in the Thermodynamic Phase Space. Reports on Mathematical Physics, 21, 197-203.
    https://doi.org/10.1016/0034-4877(85)90059-X

  46. 46. Mrugala, R., Nulton, J.D., Schön, J.C. and Salamon, P. (1990) Statistical Approach to the Geometric Structure of Thermodynamics. Physical Review A, 41, 3156-3160.
    https://doi.org/10.1103/PhysRevA.41.3156

  47. 47. Tu, L.W. (2008) An Introduction to Manifolds. Universitext. Springer Science + Business Media, LLC, New York.

  48. 48. Kluge, G. and Neugebauer, G. (1994) Grundlagen der Thermodynamik. Spektrum Akademischer Verlag, Heidelberg. (In German).

  49. 49. Abraham, R., Marsden, J.E. and Ratiu, T. (1988) Manifolds, Tensor Analysis, and Applications. 2nd Edition, Vol. 75, Springer-Verlag, New York.

  50. 50. Flanders, H. (1963) Differential Forms with Applications to the Physical Sciences. Vol. 11, Academic Press, New York.

  51. 51. Lang, C.B. and Pucker, N. (2005) Mathematische Methoden in der Physik. 2nd Edition, Spektrum Akademischer Verlag, München. (In German)
    https://doi.org/10.1007/978-3-8274-3125-7

NOTES

1The macroscopic property has obtained an identical statistically averaged value compared to its initial value, but this does not mean that the probability distribution is identical to its original distribution (nor that the microstates are identical). This observation is a severe release of constraints compared to traditional equilibrium based approaches.

2Here the concepts and notation of this paper are used, where an equilibrium state is denoted by underlined symbols (see also Section 5).

3In this context is the work of Eu [27] [28] [29] very interesting. He is aware that the Clausius definition for entropy holds only for reversible processes (e.g. equilibrium state). Eu introduces therefore a new thermodynamic quantity Calortropy, which is specified by

4See the Appendix to the Historical Indroit: Failure of Carathéodory’s attempt to set the house in order’ in the textbook on Rational thermodynamics by Truesdell (pp. 49-57 in [34] ).

5In every neighborhood of an arbitrary thermodynamic state there exist states that cannot be approached by an adiabatic process.

6Based on three assumption he introduces a simple system together with a quasi-static change of state, which is in his formulation another reference to an equilibrium state.

7Examples are: elastic deformation (with mechanical stress and strain), surface change (with surface tension and surface area), electrical polarization (with electric field and electric dipole moment), magnetic work (with magnetic field and magnetic dipole moment) and galvanic element (with electrical potential and electrical charge).

8In principle the following derivation is independent of which of the conjugated coordinates is extensive or intensive, as long as every pair contains of an extensive and an intensive quantity. But it is exactly this particular case, which will reveal that the thermodynamic potential is equal to the familiar Gibbs free energy. The result of the reverse selection of intensive and extensive quantities is shown at the end of this section.

9Quote from [44] , but modified with the conventions of this paper.

10It is here tacitly assumed that, which has to be proven for the non-equilib- rium case.

11Definition 1 introduced the non-equilibrium state function as an exact 1-form and Equation (34)1 shows that the 1-form in a Pfaffian equation is also exact. The mathematical concept of an exact 1-form originates from the area of differential manifolds (e.g. see [20] [47] [49] [50] [51] ). An arbitrary exact 1-form can be constructed as a linear combination of the differentials of the coordinates, i.e. for the 1-form can be written as

Journal Menu>>