Modern Mechanical Engineering
Vol.05 No.04(2015), Article ID:61027,10 pages
10.4236/mme.2015.54011
FE Dynamic Analysis Using Moving Support Element on Multi-Span Beams Subjected to Support Motions
Yong-Woo Kim, Seoung Yeal Lee
Department of Mechanical Engineering, Sunchon National University, Sunchon, Korea

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 12 August 2015; accepted 6 November 2015; published 11 November 2015

ABSTRACT
In the present study, finite element dynamic analysis or time history analysis of two-span beams subjected to asynchronous multi-support motions is carried out by using the moving support finite element. The elemental equation of the element is based on total displacements and is derived under the concept of the quasi-static displacement decomposition. The use of moving support element shows that the element is very simple and convenient to represent continuous beam moving, deforming and vibrating simultaneously due to support motions. The comparison between the numerical results and analytical solutions indicates that the FE result agrees with the analytical solution.
Keywords:
Moving Support Element, Support Motions, Rayleigh-Damped Bernoulli-Euler Beam, Multi-Span Beam, Time History Analysis, Finite Element Method

1. Introduction
Long and slender structures are often excited dynamically through support motions rather than by applied external loadings, e.g., piers, chimneys, towers [1] , long bridges [2] -[9] and oil pipeline subjected to ground motions. These structures in turn are responding to support motion inputs. Due to the special feature of the excitation, the effective inertial loadings are applied on structures. The structures can be represented as Euler-Ber- noulli beam subjected to multi-support motions if the foundation or ground soil is assumed to be rigid. Moreover, extended structures such as the Golden Gate Bridge and oil piping experience different ground motion at each support during an earthquake because the arrival time of seismic wave at each support is different. The vibration of the aforementioned structures is characterized as the problem of flexural vibration of beams with time-de- pendent boundary conditions. Mindlin and Goodman [10] developed the quasi-static decomposition method and applied it to obtain a solution of the problem. With this method, many researchers have investigated the structural response subjected to multiple support excitations by employing various techniques such as time history analysis, response spectrum method of analysis, frequency domain spectral analysis, etc. [11] .
According to the quasi-static decomposition method, the transverse displacement of the beam subjected to support motions is composed of the quasi-static part and dynamic part. Statically determinate beams subjected to ground motions at supports are accompanied only by quasi-static displacement of rigid-body motion. Kim and Jhung [12] presented beam elements for statically determinate beams excited by support motions and showed the FE results agree with analytical solutions. However, statically indeterminate beams subjected to non-syn- chronous support motions are involved with not only the quasi-static displacement of rigid-body motion but also the quasi-static displacement of forced deformation. For the dynamic analysis of such beams, Kim [13] developed moving support element that can describe both static forced deformation and dynamic displacement. The author illustrated a single span fixed-hinged beam subjected to asynchronous support motions to show the element’s performance. In this paper, two-span beams subjected to asynchronous multi-support motions are illustrated to show that the moving support element produces accurate dynamic responses even for the continuous beams. Since it is hardly possible to find the literature that compares numerical solutions with analytic ones, the numerical results including bending moment and shear force are compared with analytic solutions to show the high accuracy of the numerical results.
2. Multi-Span Beam Subjected to Support Motions
2.1. Rayleigh-Damped Euler-Bernoulli Beam
For a beam in flexure shown in Figure 1(a), the transverse displacement at any point x and time t is denoted by
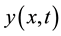 and the transverse force per unit length by
and the transverse force per unit length by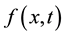 . The system parameters are the mass per unit length
. The system parameters are the mass per unit length
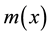 and the flexural rigidity
and the flexural rigidity , where E is Young’s modulus of elasticity and
, where E is Young’s modulus of elasticity and
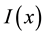 is the cross-sec- tional area moment of inertia about an axis normal to x and y and passing through the center of the cross-sec- tional area. Figure 1(b) shows the free-body diagram corresponding to a beam element of length
is the cross-sec- tional area moment of inertia about an axis normal to x and y and passing through the center of the cross-sec- tional area. Figure 1(b) shows the free-body diagram corresponding to a beam element of length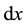 , where
, where
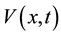 denotes the shearing force and
denotes the shearing force and
 the bending moment. According to simple beam theory, they are expressed as follows:
the bending moment. According to simple beam theory, they are expressed as follows:
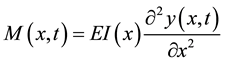 (1)
(1)
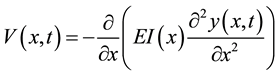 (2)
(2)
The motion of a Rayleigh-damped Euler-Bernoulli beam with uniform cross-section is described by the following partial differential equation.
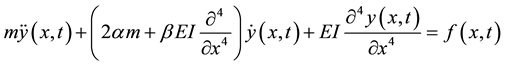 (3)
(3)

Figure 1. (a) Bending of a beam; (b) Fee-body diagram of a beam element of length .
.
where a superimposed dot denotes a time derivative, L denotes length of the beam, and
 and
and
 are coefficients of the Rayleigh damping
are coefficients of the Rayleigh damping
2.2. Continuous Beam Subjected to Support Motions
For simplicity, we consider the dynamic response of two-span Rayleigh-damped Euler-Bernoulli beams subjected to multi-support excitation, which are shown in Figure 2, and assume that the external load




where




3. Moving Support Element
3.1. F.E. Equation Based on the Total Displacements
The moving support elemental equation is given, from [13] , by

where


In Equations (9) and (10), the double prime denotes a twice spatial differentiation with respect to the element coordinates


Figure 2. A two-span beam subjected to support motions, where

Figure 3. Typical beam element (e) subjected to concentrated nodal forces (




where l is element length. In Equation (8),






where

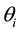






where



Note that the underlined terms in right hand side of Equation (8) are peculiar to the moving support element and they contain the quasi-static displacement and velocity. The static components can be obtained exactly by static FE analysis, which will be considered in the next section.
3.2. Static FE Analysis for Quasi-Static Displacements
According the quasi-static decomposition method, the solution can be decomposed into two parts:

where




where




and Equation (17) is subjected to the support conditions in Equations (4)-(6).
Let









The variables in Equations (18) and (19) will be called ‘quasi-static support variables’ or simply ‘support variables’ in this paper. The unknown support variables are determined by using the conventional static finite element method. The finite element equation is given by

For the hinged beam in Figure 2, the support variables are given by



and the external moments at supports are



Using Equations (21) and (22), we obtain

where

Using the support variables in Equations (21), (22) and (23), we obtain the distribution of the static displacement




where




Figure 4.






Figure 5. The beams in (a) and (b) are subjected to the seismic acceleration time histories when the earthquake traveling wave propagates longitudinally from the left support to the right ones at constant speed and the time delay between neighboring supports is 0.1 s. The seismic acceleration time history applied on the support 1 is shown in (c).
that the displacements








4. Numerical Tests
The two beams in Figure 5(a) and Figure 5(b) will be tested and the comparison between finite element outputs
and analytical solutions will be made to check the validity of the moving support element for dynamic responses of the beams due to support motions.
The input data are as follows: D1 = D2 = 60 m, EI = 2.45 × 109 N×m2, and m = 2400 kg/m; α = 0.0844 s−1 and β = 0.0141 s for the beam in Figure 5(a); α = 0.1281 s−1 and β = 0.0094 s for the beam in Figure 5(b). The initial displacement and velocity are assumed zero. Forty beam elements of the same length are used for F.E. discretization. To simulate asynchronous support excitation that induces a forced deformation, it is assumed that the seismic acceleration in Figure 5(c) is applied on the left support (i.e., support 1) at t = 0.0 s and that the earthquake traveling wave propagates longitudinally from the left support to the right ones at constant speed. Assume that the time delay between supports is 0.1 s. For the integration of the finite element equation of motion, the Newmark integration scheme is employed and the time interval is 1/1000 s.
The analytic series solutions for displacement, slope, acceleration, moment and shear force are obtained by eigenfunction expansion method with 10 modes. The numerical results such as displacement, velocity and acceleration at x = 30 m are compared with their analytical solutions in Figure 6 and Figure 7. The FE solutions of displacement, slope, bending moment and shear force along the beams at some instants are also compared with their analytic solutions in Figure 8 and Figure 9. They show that the numerical results agree with analytical responses.
5. Conclusion
FE dynamic analysis or time history analysis on the two-span Rayleigh-damped Bernoulli-Euler beams subjected to asynchronous support motions is carried out by using the moving support element. And the corresponding analytical solutions are obtained by using eigenfunction expansion method with 10 modes. The numerical results such as displacement, velocity, acceleration, slope, bending moment and shear force are compared


Figure 6. The motions of the beam in Figure 5(a). (a) Displacement at x = 30 m; (b) Velocity at x = 30 m; (c) Acceleration at x = 30 m.


Figure 7. The motions of the beam in Figure 5(b). (a) Displacement at x = 30 m; (b) Velocity at x = 30 m; (c) Acceleration at x = 30 m.


Figure 8. Reponses of the beam in Figure 5(a) along the beam at t = 10.18 sec. (a) Displacement along the beam; (b) Moment along the beam; (c) Slope along the beam; (d) Shear force along the beam.


Figure 9. Reponses of the beam in Figure 5(b) along the beam at t = 12.34 sec. (a) Displacement along the beam; (b) Moment along the beam; (c) Slope along the beam; (d) Shear force along the beam.
with the analytical ones to show that the moving support element describes moving, deforming and vibrating of multi-span beams subjected to support motions accurately. The numerical results agree with analytical solutions well.
Cite this paper
Yong-WooKim,Seoung YealLee, (2015) FE Dynamic Analysis Using Moving Support Element on Multi-Span Beams Subjected to Support Motions. Modern Mechanical Engineering,05,112-121. doi: 10.4236/mme.2015.54011
References
- 1. Abdel-Ghaffar, A.M. and Rood, J.D. (1982) Simplified Earthquake Analysis of Suspension Bridge Towers. Journal of the Engineering Mechanics Division, ASCE, 108, EM2, 291-308.
- 2. Harichandran, R. and Wang, W.J. (1990) Response of Indeterminate Two-Span Beam to Spatially Varying Seismic Excitation. Earthquake Engineering and Structural Dynamics, 19, 173-187.
http://dx.doi.org/10.1002/eqe.4290190203 - 3. Chen, J.T., Hong, H.-K., Yeh, C.S. and Chyuan, S.W. (1996) Integral Representations and Regularizations for a Divergent Series Solution of a Beam Subjected to Support Motions. Earthquake Engineering and Structural Dynamics, 25, 909-925.
http://dx.doi.org/10.1002/(SICI)1096-9845(199609)25:9<909::AID-EQE591>3.0.CO;2-M - 4. Yau, J.D. and Fryba, L. (2007) Response of Suspended Beams Due to Moving Loads and Vertical Seismic Ground Excitations. Engineering Structures, 29, 3255-3262.
http://dx.doi.org/10.1016/j.engstruct.2007.10.001 - 5. Fryba, L. and Yau, J.-D. (2009) Suspended Bridges Subjected to Moving Loads and Support Motions Due to Earthquake. Journal of Sound and Vibration, 319, 218-227.
http://dx.doi.org/10.1016/j.jsv.2008.05.012 - 6. Liu, M.-F., Chang, T.-P. and Zeng, D.-Y. (2011) The Interactive Vibration in a Suspension Bridge System under Moving Vehicle Loads and Vertical Seismic Excitations. Applied Mathematical Modelling, 35, 398-411.
http://dx.doi.org/10.1016/j.apm.2010.07.005 - 7. Yau, J.D. (2009) Dynamic Response Analysis of Suspended Beams Subjected to Moving Vehicles and Multiple Support Excitations. Journal of Sound and Vibration, 325, 907-922.
http://dx.doi.org/10.1016/j.jsv.2009.04.013 - 8. Lin, J.H., Zhang, Y.H., Li, Q.S. and Williams, F.W. (2004) Seismic Spatial Effects for Long-Span Bridges, Using the Pseudo Excitation Method. Engineering Structures, 26, 1207-1216.
http://dx.doi.org/10.1016/j.engstruct.2004.03.019 - 9. Zhang, Y.H., Li, Q.S., Lin, J.H. and Williams, F.W. (2009) Random Vibration Analysis of Long-Span Structures Subjected to Spatially Varying Ground Motions. Soil Dynamics and Earthquake Engineering, 29, 620-629.
http://dx.doi.org/10.1016/j.soildyn.2008.06.007 - 10. Mindlin, R.D. and Goodman, L.E. (1950) Beam Vibrations with Time-Dependent Boundary Conditions. Journal of Applied Mechanics, ASME, 17, 377-380.
- 11. Datta, T.K. (2010) Seismic Analysis of Structures. John Wiley & Sons (Asia) Pte Ltd., Singapore.
http://dx.doi.org/10.1002/9780470824634 - 12. Kim, Y.-W. and Jhung, M.J. (2013) Moving Support Elements for Dynamic Finite Element Analysis of Statically Determinate Beams Subjected to Support Motions. Transactions of the Korean Society of Mechanical Engineers A, 37, 555-567.
http://dx.doi.org/10.3795/KSME-A.2013.37.4.555 - 13. Kim, Y.-W. (2015) Finite Element Formulation for Earthquake Analysis of Single-Span Beams Involving Forced Deformation Caused by Multi-Support Motions. Journal of Mechanical Science and Technology, 29, 461-469.
http://dx.doi.org/10.1007/s12206-015-0106-1











