Modern Mechanical Engineering
Vol.05 No.02(2015), Article ID:56526,12 pages
10.4236/mme.2015.52004
Dry Friction with Various Frictions Laws: From Wave Modulated Orbit to Stick-Slip Modulated
Paul Ndy Von Kluge*, Djuidjé Kenmoé Germaine, Kofané Timoléon Crépin
Department of Physics, Mechanics Laboratory, Faculty of Sciences, University of Yaoundé 1, Yaoundé, Cameroon
Email: *kdjuidje@yahoo.fr
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 March 2015; accepted 19 May 2015; published 22 May 2015
ABSTRACT
Choices of excitation signals are important in engineering sciences and in physical simulations; a sufficient excitation can be critical in modelling a complicated nonlinear dynamic system. The discontinuous dynamic of a non-linear, friction-induced with two idealized periodical forced oscillators is studied. The dry friction in the system follows the classical Coulomb law, and various friction characteristics of dry friction laws in engineering sciences. To capture the presence of the two driving forces, the system must be studied as a function of their frequency-modulated and its equivalent amplitude modulated waveforms. Our numerical investigation shows a rich dynamical behaviour including periodic, quasi-periodic motions, thus a variable dynamics phenomenon among others; such as modulated waves, modulated stick-slip, periodic oscillation, and periodic stick-slip. It seems that such excitation forces can be used to conveniently identify the existence of nonlinearity, dry friction effects, and strength degradation in the system. The results achieved via the Coulomb’s law are compared with those obtained via two others particular friction laws: the complete model with Stribeck effect and Coulomb viscosity.
Keywords:
Dry Friction, Stick-Slip, Wave Modulated, Stick-Slip Modulated

1. Introduction
In general, there are many different types of dry friction models and it is crucial to appropriately choose one which best suits to the modelled problem, however choices of excitation forces have been widely studied for the modal testing community [1] . In system identification, the need to investigate proper excitation forces has been recognized even for a system without memory [2] . For many years the topic of dry friction has been actively researched with many attempts to identify the causes of unwanted behaviour [3] - [5] . Friction-induced vibration, chatter and squeal [6] cause serious problems in many industrial applications, including turbine blade joints, robot joints, electric motor drives, water-lubricated bearings in ships and submarines, wheel/rail coupling of mass transit systems, machine tool/work piece systems and brake systems. These forms of vibration [7] can cause excessive wear of components: surface damage, fatigue failure, and noise.
From the mathematical point of view, the appearance of the discontinuous differential equations is usual, where the character of this discontinuity depends on the friction character adopted [8] , but seeking an effective means of decoupling the complexity of excitations from that of the nature of the system is important. The presence of Coulomb friction makes the analysis of the problem challenging due to the dependence of the friction force on the velocity in a complicated and discontinuous manner. If one considers dynamics of the system where the relative velocity practically remains constant, there is no need for sophisticated dry friction models and even the easiest one described by the Coulomb law will be enough. However in many cases, the variation of relative velocity is large and often the velocity changes its sign [9] . But when adding other particular friction laws such as complet model with Stribeck effect or Coulomb + viscosity, other complicated phenomenons occur. Systems with dry friction possess many different types of dynamical behaviour [10] , such as periodical oscillation and periodical stick-slip. An approximate analysis of stick-slip vibration is based on dividing the motion into two phases: a stick phase in which the velocity of the motion is constant and a slip phase in which the motion is approximated as a circular (pure sinusoidal) motion with constant amplitude. The solutions of the two phases are batched together. Applying oscillation force sometimes to control the system moves the system from stick-slip to smooth sliding.
The “mass on belt system” falls within the category of hybrid system or switching system [11] [12] . The switching behaviour is brought in by the play of dry friction originating between the surface of the mass and the belt. The mass can either be in a stick mode or a slip mode and this creates a switching type system. Friction induced and self-excitation oscillations are affected by high-frequency external excitations [13] . Friction properties change under the action of fast vibration. Generally, high-frequency excitations can reduce or totally suppress friction-induced vibrations [14] . This study considers how such friction properties in two contact surfaces are changed in the presence of two external excitations. Among the vibration characteristics used, the vibration amplitude is especially important because it can directly affect stresses and thus the life of the system. The friction model is a sign function plus linear and cubic function of the relative velocity [15] . In the present work, we further our study into the dynamics of a single-degree-of-freedom system with dry friction and two harmonic driving forces. The aim is to understand how the response of the system is affected by the amplitude modulated and the ratio of the frequencies modulated of the two driving forces using either the Coulomb’s law or other particular friction laws.
2. Model Description and Equation of the Motion
2.1. Model Description
The system under investigation is shown in Figure 1, where a mass m is connected to a fixed support via a linear spring with stiffness k and a viscous damper coefficient c. This oscillator slides or rests on the horizontal belt surface travelling with a constant speed v0. Consider two harmonic driving forces exerting on the mass with the same amplitude p0, but different frequencies w1 and w2, these forces are defined as
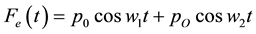 (1)
(1)
The two excitation frequencies are proportional to each other in such a way that
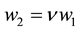 (if ν = 1, the force degenerates to a single excitation case). The dry friction between the interfaces can follow Coulomb’s law (characterized by the static coefficient µs and the smaller kinetic coefficient µk) or other frictions laws. Since the mass contacts the moving belt with friction, the mass can move along or rest on the belt. The equation of motion for such a friction-induced oscillator is:
(if ν = 1, the force degenerates to a single excitation case). The dry friction between the interfaces can follow Coulomb’s law (characterized by the static coefficient µs and the smaller kinetic coefficient µk) or other frictions laws. Since the mass contacts the moving belt with friction, the mass can move along or rest on the belt. The equation of motion for such a friction-induced oscillator is:
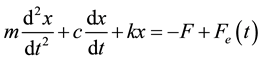 (2)
(2)
Figure 1. Model of the single-degree-of freedom friction oscillator excited by moving base and two driving forces.
where x denotes the displacement of the mass. FN is the normal force in the contact area, i.e. The weight of the block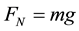 .
.
With a non smooth transition, the resulting motion also shows a non smooth behaviour. The stick-slip systems belong to the class of non smooth systems, such as systems with stops, impacts, backlash or hysteresis. The nature of dynamic friction forces developed between bodies in contact is extremely complex and affected by a long list of factors: the constitution of the interface, the time scales and the frequency of the contact, the response of the interface to normal forces, inertia and thermal effects [16] , roughness of the contacting surfaces [17] . The dry friction force F depends on the relative speed of the surfaces in contact and can be defined as:
 (3)
(3)
where a1and a3are friction coefficient, and
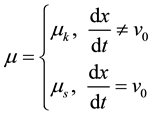 (4)
(4)
The relative velocity of the contact can be defined as:
 and
and
 (5)
(5)
The significant role of various dry friction laws in engineering sciences can be illustrated in Figure 2. The friction characteristic described with Coulomb law is shown in Figure 2(a). The friction model does not specify the friction force for zero velocity. Figure 2(b) shows the case of coulomb + viscosity while Figure 2(c) illustrates the friction with Stribeck effect.
2.2. Equation of Motion
The equation of motion Equation (2) can be normalized using:
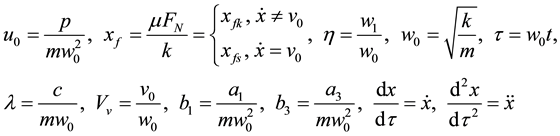 (6)
(6)
where τ is dimensionless time coordinate, w0 is the frequency of free oscillations of the mass.
Equation (2) can be rewritten then in a dimensionless form as:



Figure 2. Velocity-dependent frictions laws giving by Equation (3): (a) non-smooth Coulomb law: (a1 = 0.0, a3 = 0.0); (b) Coulomb + viscosity: (a1 = 0.2, a3 = 0.0); (c) Complete model with Stribeck effect: (a1 = 0.2, a3 = 0.16).
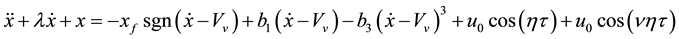 (7)
(7)
The choice of one of the friction laws shown in Figure 2 can be obtained by monitoring the parameters b₁ and b3 (dimensionless friction coefficient).
3. Dynamic Responses
3.1. Analytical Treatment of the Motion of the Block
In the case where b1 = b3 = 0, one can treat Equation (7) analytically to show amplitude motion which occurs in the sliding phase. Assume that the motion starts when the block sticks on the belt,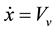 . The general form of the solution of Equation (7) can be write as
. The general form of the solution of Equation (7) can be write as
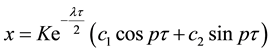 . It is the sum of the homogenous solution and the particular solution. If
. It is the sum of the homogenous solution and the particular solution. If

where

With the initial conditions

It is noted that the upper and lower part of the compound signs in Equation (8) corresponds to the case of


An important idea associated with the response of an oscillator to the periodic force is resonance i.e., when the natural frequency of the oscillator is equal to the frequency of the periodic force. Figure 3 displays the evolution of the amplitude as a function of the parameter η. The curves of amplitude versus the ratio η show a resonance near the value η = 1, i.e., when the frequency w₁ is near the natural frequency w₀. The height of the peak depends on the applied u₀, the damped coefficient λ, as well as on the ratio of the force excitation frequencies ν. For smaller values of λ in Figure 3(c), the current frequency curve is sharply peaked, but for large values of λ the curve is flat.
3.2. Numerical Treatment
We further our study, in order to know how the response of the system is affected by the two harmonic driving forces. Numerical investigation will be done firstly, by using Coulomb’s law and secondly with numerical investigation by assuming two others particular friction laws as mention above.
3.2.1. Numerical Analysis of the Motion of the Block
In order to understand dynamical processes in our model, Equation (7) has been integrated numerically using fourth-order Runge-Kutta scheme with time step Δt = 0.04. The results of this numerical investigation are shown in Figures 4-7, in which we obtained unless otherwise specified [18] , for λ = 1/2, η = 3/5, Vv = 1,



Through a series of numerical simulations, it seems that such excitation forces can be used to conveniently reproduce the stick-slip behaviour of ice streams in glaciology [19] . However, in the system, we observe two


Figure 3. Amplitude as a function of frequency








Figure 4. Modulated Motion without stick (top): (a) angular modulated: WM1 (n = 0.10; u0 = 0.2); (b) Amplitude Modulated: WM2 (n = 0.95; u0 = 0.05) and corresponding velocity time history (bottom).


Figure 5. Modulated Motion with stick phase (SSM1): (a) (n = 0.10; u0 = 1.15); (b) n = 0.2; u0 = 3.05) and corresponding velocity time history (bottom).
types of modulation: simple wave modulation and stick-slip modulation. Acronyms like “WM” and “SSM” stand for “wave modulated” and “stick-slip modulated”, respectively. Depending on the amplitude u0 and the ratio of the two frequencies


Figure 6. Modulated amplitude stick-slip (SSM2); corresponding velocity time history (n = 1.15; u0 = 0.7).

Figure 7. Periodic stick slip motion: (a) Periodic Oscillation: η = 1/5; n = 1.0; u0 = 1.65; (b) Corresponding velocity time history.
a) Wave modulated: we observed two types; wave modulated 1 (WM1) which corresponds to the angular modulated wave and wave modulated 2 (WM2) which refers to amplitude modulated. Figure 4 illustrates these forms of modulation with the corresponding time velocity obtained with the set parameter

b) Stick-slip modulated: here the dynamics of the system presents modulated motion with stick phase. We observed two types regarding the form of the modulation of excitation force. Figure 5 presents stick-slip modulated 1 (SSM1) which corresponds to the angular modulated stick-slip with the corresponding time velocity obtained with the set parameter n = 0.1, u0 = 1.15 and n = 0.2, u0 = 3.05. At the stick phase, the velocity remains constant and equal to the driving velocity Vv = 1, but the amplitudes of the block velocity during slipping are modulated. The stick phase is significantly presents here because of the effect of dry friction which predominated the dynamics of the system in comparison with the first case where the excitation forces influence significantly.
In Figure 6 there is no stick in all the motion cycle, but the velocity is modulated at slip phase. Figure 6 presents stick-slip modulated 2 (SSM2) which corresponds to the amplitude stick-slip, this phenomenon occur for the set parameter n = 1.15, u0 = 0.7.
c) Periodic stick-slip and periodic oscillation: regarding the form of the excitation force, periodic stick slip occurs with integer values range of n. As n becomes an integer multiple, n, of the forcing ratio of the excitation frequency, the system has gone into periodic oscillation. The force degenerates to a single excitation case for n = 1. Figure 7 presents a periodic stick slip i.e., without any modulation and the corresponding time velocity obtained with the set parameter η = 1/5, u0 = 1.65, n = 1.0.
3.2.2. Parameter’s Map and Influence of Friction Laws
As an aid in describing and understanding nonlinear systems, someone can introduce maps in this section. In order to develop a meaningful understanding of friction experiments, and to predict dynamic system response and performance, an influence of the friction model must be studied. Although models predict well-defined stick-slip frequencies, intervals between successive stick-slip events have relatively broad distributions. For a better understanding of the map, the x-axis represents the amplitude of the applied u₀ response while, the y-axis represents the excitation frequency n. The first curve indicated the boundary between the Wave Modulated(WM) motion and the Stick-Slip Modulated (SSM), and the second curve indicated the limit between the end of (SSM) motion and the continue intermittent (WM). From the parameter maps, it is observed that specific motion lies on the special region of the parameters.
Figure 8 shows the dynamical phase diagram (in the n-u0 plane), which presents regions of the ratio excitation frequency that correspond to different regimes of the motion of the block. Wave modulated 1 (WM1) and




Figure 8. Parameters map of (u0; n) using Coulomb law: (b1 = 0.0; b3 = 0.0; λ= 1/2; Vv = 1): (a) η = 1/9; (b) η = 1/5; (c) η = 5/3; (d) η = 7/3.
Wave modulated 2 (WM2) motion occur, respectively, to the left and right at the first and second line (with n < 1) and to the left-right of the first-second line (with n > 1). The system exhibits stick-slip modulated (SSM) motion in the range of parameters between these two curves. The two lines describe the n dependence of the applied u₀ corresponding to the transitions between different states of motion. The parameter η gives the orientation of these two curves. For instance, in Figure 8(a) and Figure 8(b), η is very weak, respectively 0.11 and 0.2, that make the slop of limits curve lying to the left side of the diagram close to n-axis apses, this prove that the applied u₀ decreases significantly. The important observation is that for n comprises in between 1 and 3, the value of stick-slip modulated (SSM₂) is mostly nil in Figure 8(a), [respectively nil in Figure 8(b)], and some values of u₀ are not inside the diagram for certain values surrounding the frequency n = 1. When n out dated the value 3 to u₀ weak, the stick-slip bandwidth is large.
As an interesting details, one can observe that if w1 smaller than the natural frequency w₀, the bandwidth became bigger as n increase and for weakest values of η, the stick-slip modulated begin for very large values of u₀, the response to a periodic oscillation is described in all figures in parameter maps for integer ratio n outcast stick-slip band. The bright reflecting type points indicated the stick-slip modulated inside stick-slip band and the dash one represent the periodic stick-slip. For larger values of the excitation amplitude depending on the excitation frequency, the friction oscillator shows periodic motions modulated.
When n is very weak, we have u₀ very large in Figure 8(b), we observed the presence of periodic stick-slip in between the stick-slip bandwidth for the integer value of n while the periodic oscillation in two extreme of always integer value of n. We also observe that the stick-slip modulated (SSM₁) ends for n = 1 while stick-slip modulated (SSM₂) begins from n > 1. Figure 8(c) and Figure 8(d) illustrated the case where η > 1 and the two




Figure 9.Parameters map of (u0; n) using Coulomb + viscosity: (b1 = 0.2; b3 = 0.0; λ= 1/2; Vv = 1): (a) η = 1/9; (b) η = 5/17; (c) η = 5/3; (d) η = 7/3.
curves are lying to the right of the diagram. As the friction force increases, the stick motion is suppressed in Figure 8(d), (η = 2.33) [respectively in Figure 8(c) (η = 1.67)]. Note that the stick-slip motion tends to disappear if w₁ is bigger than w0 in the ratio η so that the big values of η diminish significantly the bandwidth of stick-slip. Using this parameter map the system behaviour can be characterized for any set of parameters within the plotted range.
Using the same parameters system as in Figure 8, we reproduce the simulation with the two other friction forces mention above. In the case of the friction with Coulomb + viscosity, (b₁ = 0.2; b₃ = 0.0), Figure 9 shows the same observations as above, but the SSM1 is mostly nil or outside the n− u0 plane. If n ∊ [2] [3] the bandwidth SSM tend to disappear (very weak). For η = 0.29, the two limits curves are relatively straight in Figure 9(b). But Figure 9(c) and Figure 9(d) illustrated the curve with w₁ greater than w₀, the amplitude u₀ takes very large values, the stick-slip band become very weak. In the mapping procedure, special attention has to be paid to the lower or the higher values of the ratio η. we observed a diminishingly amplitudes u0 if the frequency w₁ is less than w₀. The features of high amplitude and high n-factor are clearly recognized.
In the case of Stribeck friction,

another parameter map showing the influence of the excitation amplitude u0 is represented and the stick-slip phenomenon disappear partially in Figure 10(d).


Figure 10. Parameters map of (u0; n) using Stribeck friction laws: (b1 = 0.2; b3 = 0.16; λ= 1/2; Vv =1): (a) η = 1/9; (b) η = 1/5; (c) η = 3/5; (d) η = 7/3.
4. Conclusion
The first main purpose of this paper was to investigate the influence of the frequencies, in external excitation with two harmonic driving forces in the case of a moving base. The second main purpose was to show the influence of various friction characteristics and parameter maps on the system response. Numerical and analytical predictions of the scenarios varying with the ratios of the two excitation frequencies and amplitudes are carried out, and the parameter maps for specific motions are presented. This study suggests that, the transition between each of the motions strongly depends on the parameters (frequencies and amplitudes) of the two driving forces; this was appreciated in the analytical result. The applying two driving forces were also found to give rise to stick-slip modulation. We observed the amplitude modulation of the velocity during slip phase. These and other results contribute to the general understanding of how friction properties may change under the action of the two vibrating forces. If two harmonics of almost periodic excitation are interacted, modulated motions take place. But we must control the ratio η to control the dynamic of the system. In all mechanical system, Stick-Slip motion is considered as harmful effects. So that too many researches are concentrated to diminish amplitude of vibration which can directly affect stresses and thus the life of the system and our results have potentially an equally wide range of applications in engineering.
References
- Ewins, D.J. (2001) Modal Testing: Theory, Practice and Application, Mechanical Engineering Research, Studies Engineering Design Series. Research Studies Pre, 2nd Edition.
- Piyawat, K. and Pei, J.S. (2005) Idealized Excitation Forces for Nonlinear SDOF Systems with Memory and Degradation. School of Civil Engineering and Environmental Science, The University of Oklahoma, Norman.
- Den Hartog, J.P. (1931) Forced Vibrations with Combined Coulomb and Viscous Friction. Trans ASME, 53, 107-115.
- Wojewoda, J., Kapitaniak, T., Barron, R. and Brindley, J. (1993) Complex Behaviour of a Quasiperiodically Forced System with Dry Friction. Chaos, Solitons & Fractals, 3, 35-46. http://dx.doi.org/10.1016/0960-0779(93)90038-3
- Shaw, S.W. (1986) On the Dynamic Response of a System with Dry Friction. Journal of Sound and Vibration, 108, 305-325. http://dx.doi.org/10.1016/S0022-460X(86)80058-X
- Ibrahim, R. (1994) Friction Induced Vibration, Chatter, Squeal and Chaos―Part I: Mechanics of Contact and Friction. Applied Mechanics Review, 47, 209-226. http://dx.doi.org/10.1115/1.3111079
- Andreaus, U. and Casini, P. (2001) Dynamics of Friction Oscillators Excited by a Moving Base and/or Driving Force. Journal of Sound and Vibration, 245, 685-699. http://dx.doi.org/10.1006/jsvi.2000.3555
- Stefannski, A., Wojewoda, J., Wiercigroch, M. and Kapitaniak, T. (2003) Chaos Caused by Non-Reversible Dry Friction. Chaos, Solitons and Fractals, 16, 661-664. http://dx.doi.org/10.1016/S0960-0779(02)00451-4
- Wiercigroch, M., Vwt, S. and Zfk, L. (1999) Non-Reversible dry Friction Oscillator: Design and Measurements. Proceedings of the Institution of Mechanical Engineers, 213, 527-534.
- Fenny, B. and Moon, F.C. (1994) Chaos in a Forced Dry Friction Oscillator: Experiment and Numerical Modelling. Journal of Sound and Vibration, 170, 303-323. http://dx.doi.org/10.1006/jsvi.1994.1065
- Kardan, I., Kabganian, M., Abiri, R. and Bagheri, M. (2013) Stick-Slipconditions in the General Motion of a Planar Rigid Body. Journal of Mechanical Science and Technology, 27, 2577-2583.
- Cao, Y. and Chen, X.B. (2015) An ARX-Based PID-Sliding Mode Control on Velocity Tracking Control of a Stick- Slip Piezoelectric-Driven Actuator. Modern Mechanical Engineering, 5, 10-19. http://dx.doi.org/10.4236/mme.2015.51002
- Thomsen, J.J. (1999) Using Fast Vibrations to Quench Friction-Induced Oscillations. Journal of Sound and Vibration, 228, 1079-1102. http://dx.doi.org/10.1006/jsvi.1999.2460
- Cheng, G. and Zu, J.W. (2004) Dynamics of a Dry Friction Oscillator under Two-Frequency Excitations. Journal of Sound and Vibration, 275, 591-603. http://dx.doi.org/10.1016/j.jsv.2003.06.027
- Awrejcewics, J. and Dzyubak, L. (2003) Stick-Slip Chaotic Oscillations in Aquasi-Autonomous Mechanical System. International Journal of Nonlinear Sciences and Numerical Simulation, 4, 155-160.
- Awrejcewicz, J. and Pyryev, Yu. (2002) Thermo Elastic Contact of a Rotating Shaft with a Rigid Bush in Conditions of Bush Wear and Stick-Slip Movements. International Journal of Engineering Science, 40, 1113-1130.
- Voldrich, J. (2009) Modelling of Three-Dimensional Friction Contact of Vibrating Elastic Bodies with Rough Surfaces. Applied and Computational Mechanics, 3, 241-252.
- Reinhorn, A.M. and Sivaselvan, M.V. (2000) Hysteretic Models for Deteriorating Inelastic Structures. ASCE Journal of Engineering Mechanics, 126, 633-640. http://dx.doi.org/10.1061/(ASCE)0733-9399(2000)126:6(633)
- Sergienko, O.V., Macayeal, D.R. and Bindschadler, R.A. (2009) Stick-Slip Behavior of Ice Streams: Modelling Investigations. Annals of Glaciology, 50, 87-94.
NOTES
*Corresponding author.














