Modern Mechanical Engineering
Vol.05 No.01(2015), Article ID:53928,9 pages
10.4236/mme.2015.51002
An ARX-Based PID-Sliding Mode Control on Velocity Tracking Control of a Stick-Slip Piezoelectric-Driven Actuator
Y. Cao, X. B. Chen
Department of Mechanical Engineering, University of Saskatchewan, Saskatoon, Canada
Email: yuc150@mail.usask.ca
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 January 2015; accepted 8 February 2015; published 11 February 2015
ABSTRACT
Piezoelectric-driven stick slip actuators have been drawn more and more attention in the nano- positioning application due to the high accuracy and theoretical unlimited displacement. However, the hysteresis of piezoelectric actuator (PEA) and the nonlinear friction force between the end- effector and the stage make control of piezoelectric-driven stick slip actuator challenge. This paper presents the development of an autoregressive exogenous (ARX)-based proportional-integral- derive (PID)-sliding mode control (SMC) for the velocity tracking control of the piezoelectric-dri- ven stick slip actuator. Stability is guaranteed by rigorously choosing the appropriate PID parameters and the zero steady state error is achieved. To verify the effectiveness of the proposed method, experiments were carried out on a commercially-available piezoelectric-driven stick slip actuator. The tracking errors were compared with the traditional PID controller, illustrating that in spite of existing of modeling error, the ARX-based PID-SMC is able to better improve the velocity tracking performance of piezoelectric-driven stick slip actuator, compared with the traditional PID controller.
Keywords:
Autoregresive Progress, Sliding Mode Control, Slick-Slip, Piezoelectric Actuator

1. Introduction
Piezoelectric-driven stick-slip actuators play important roles in nano-positioning applications due to their simple configuration, high accuracy and theoretically unlimited displacement [1] -[6] . The end-effector is supported and guided by a movable stage, which is connected to the base through flexible hinges and driven by a PEA, as shown in Figure 1. The end-effector moves together with the stage under slow expansion of the PEA. Sudden contraction of the PEA leads to the sliding motion of the end-effector since the force due to the friction limit between the end-effector and the movable stage. As a result, the end-effector moves a step ΔS, with respect to its original position. Such steps can be accumulated to achieve a theoretically unlimited displacement (actually limited by the size of the moveable stage).
The hysteresis of PEA and the friction dynamics of the end-effector make the control of stick-slip actuator challenge. An analog electronic circuit was developed in [7] for driving stick-slip piezoelectric linear actuators. The key design task for the amplifier is to provide a high-voltage asymmetric sawtooth-like signal and feed it into a capacitive load. To compensate the hysteresis effect, combination of a charge control scheme with switch- ing is proposed and the experiments confirm the superiority of the proposed method over other existing techniques. However, the charge control requires expensive hardware, which increases the difficulty and cost of its implementation. To avoid this, a voltage/frequency proportional controller was proposed in [8] for high stroke displacement of stick-slip micro-positioning stage. The proposed controller is essentially a combination of the sign controller, the classical proportional control and frequency proportional control, and the experimental results showed its priority over the basic controller. To compensate the steady state error, integral control was employed in addition to the aforementioned method [9] . In [10] , Proportional-Derivative (PD) controller was applied in the control of the stick slip piezoelectric actuators. Its application in the sample holder for Atomic Force Microscope (AFM), the micro-Electrical Discharge Machining (EDM) machine, the micro-assembly system and the micro tele-manipulation system for biological specimens was described.
All the research mentioned above related to the displacement tracking control of the piezoelectric-driven stick-slip actuators under step or ramp reference signal. The velocity tracking control has not been reported yet. This work focuses on the development of control method for the velocity tracking control of the piezoelectric- driven stick-slip actuators.
PID/PI/PD controller has shown great potential in the control application for nano-positioners. The challenge of PID/PI/PD control in the velocity tracking control of stick-slip piezoelectric-driven stage is maintaining the system stability in the presence of uncertainty and disturbance. It also has an issue with low gain margin in high frequency applications [1] . Recently, sliding model control (SMC) has been drawing considerable attention in the control research community worldwide due to its ability to compensate for the system uncertainties and disturbance [11] -[14] . To solve the chattering problem of the regular SMC, a PID-based SMC (PID-SMC) was developed in [15] , in which the discontinuous “bang-bang” switching function is replaced by a PID regulator. Due to the integral effect of the PID regulator, zero steady state tracking error can be achieved.
Figure 1. Working principle of the piezoelectric-driven stick- slip actuator.
As a state tracking control scheme, the PID-SMC developed in [15] has been shown effective in the control of the second order mechanical systems, in which the states can be readily estimated from the measured output and/or its derivatives. In some circumstances, the system state might not be readily or even be impossibly obtained due to system complexity. In such a case, the application of PID-SMC is challenged due to the lack of system state information. For this, an output tracking integrated PID-SMC is developed [16] , in which the transfer function of the plant is considered to be a cascade of the numerator and the denominator. The numerator is compensated by an optimal inverse feedforward controller and as such the regular state tracking based SMC can be applied. The proposed method has been experimentally shown effective in the control of a commercially available one-degrees-of-freedom (DOF) piezoelectric actuator.
It is noted that if the dynamics of the plant can be represented by an auto-regressive (ARX) model without
zeros, for example, 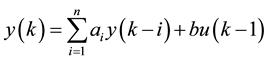 , where u(k) and y(k) are the system input and output at
, where u(k) and y(k) are the system input and output at
time instant k respectively, such a model will be readily transferred to a state space model with its state being the system output and the state tracking based PID-SMC is able to be directly applied for the dynamics compensation. Inspired by this, an ARX-based PID-SMC is developed in this paper and applied in the velocity control of a one-DOF stick-slip PEA. The effectiveness of the proposed method is experimentally verified and compared with the traditional PID controller introduced in [9] .
2. ARX-Based PID-SMC and Its Design
The discrete nth order plant might be generally described by the following transfer function
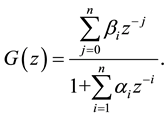 (1)
(1)
where 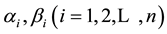 and
and  are the parameters and the numerator and denominator are relatively prime polynomials. With the use of the system identification method, this plant model can be mathematically repre- sented by an ARX model.
are the parameters and the numerator and denominator are relatively prime polynomials. With the use of the system identification method, this plant model can be mathematically repre- sented by an ARX model.
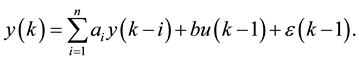 (2)
(2)
Equation (2) is identical to a discrete transfer function without zeros. The neglect of zeros definitely leads to model errors, which is considered to be disturbance in Equation (2).
The ARX model can be rewritten in a state space form
 (3)
(3)
where  is the state vector;
is the state vector; 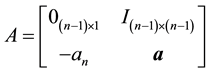
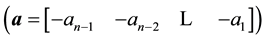 ,
,  and
and 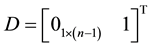 are the system matrixes of the
are the system matrixes of the
discrete state space model. The state vector is represented in terms of the outputs in the past history, which suggest the state tracking is essentially the output tracking. Therefore, the state tracking SMC design method can be applied.
Denote the desired output vector to be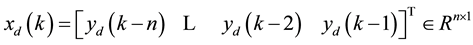 . The object-
. The object-
tive of SMC is to force the error state 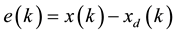 to move to the sliding surface and then converge to zero. Equation (3) can be rewritten in terms of the dynamics of e(k),
to move to the sliding surface and then converge to zero. Equation (3) can be rewritten in terms of the dynamics of e(k),
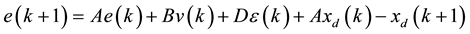 . (4)
. (4)
Similar to the general SMC design approach introduced in [15] , the input u(k) is divided into two parts  and
and 

It is noted that Equation (5) is non-casual if the future desired output is unknown. In such a case, 

Substituting Equation (5) into Equation (4) yields

For the system described by Equation (3), one has

For the sliding function that takes the following form of

The control action can be considered consisting two parts, i.e.,

where 

Substituting Equation (10) into Equations (8) and (9) yields


For the convenience of following discussion, Equations (9) and (11) are rewritten as

where 
where 

where P, I and D are parameters of the discrete PID-based SMC; T is the sampling period.
Theorem 1: If the closed-loop system (13) is stable, the zero steady state error can be achieved [17] .
Theorem 2: There exist some P, I and D such that the closed-loop control system (13) is stable [16] .
3. Experiments
To verify the effectiveness of the proposed method, experiments were carried out to control the motion velocity of a stick-slip piezoelectric-driven actuator (Figure 2). The PEA used to drive the stage generates displacement in a range of 15 μm with a resolution of 0.5 nm. An inductive sensor (SMU9000, Kaman, Windsor, CT) with a resolution of 10 nm was used to measure the displacement of the end-effector. Both the actuator and the sensor were connected to a host computer via an I/O board (PCI-DAS1602/16, Measurement Computing Corporation) and controlled via SIMULINK programs. The movable stage is driven by the PEA and the end-effector on the stage can slide horizontally on the stage via a pair of V grooves machined on them. Polished silicon wafers are attached to the V grooves as frictional surfaces to guarantee the uniformity of the frictional characteristics throughout the traveling range of the end-effector. All the displacements presented in this study were measured by the inductive sensor with a sampling interval of 0.05 ms.
Figure 3 shows the model configuration of the stick-slip piezoelectric-driven stage developed in [18] .

Figure 2. Experimental settings on the piezoelectric driven stage; (a) schematic and (b) picture.
Figure 3. Model configuration of the piezoelectric-driven stick-slip actuator (Regenerated from [18] ).
Me is the mass of the end-effector, Ff is the friction force between the PEA stage and the end-effector. The hysteresis model H is cascaded with the vibration dynamics model. The output―PEA displacement is feed- forward to the friction model, which generates the friction force and the motion parameters of the end-effector.
To apply the ARX-based PID-SMC, the PEA and the end-effector are considered to be an integrated system with its input being the driven voltage u and its output being the motion velocity of the end-effector, as shown in Figure 3. The nonlinearities such as hysteresis and the friction are considered to be disturbances and then rejected by the proposed method. Experiments for parameter identification were first carried out to obtain the ARX model. Then, the ARX-based PID-SMC was applied to control the nano-postioning stage for tracking step reference signals. Finally, dynamic tracking control with the proposed methods was implemented and comparison to a PID controller was made.
3.1. Model Identification
To drive the end-effector, a saw-tooth generator is required, as seen in Figure 4. Each saw-tooth is 20 ms wide. The amplitude of the each saw-tooth is defined by the reference input voltage u(t). If u(t) < 0, a reverse saw-
Figure 4. Saw-tooth generator for the stick-slip motion and the velocity calculator.
tooth signal is demanded to move the end-effector to the backward direction, as shown in Figure 5. The driven voltage supplied to the PEA 

where T is the tooth width, mod represents the modulus after division.
The displacement of the end-effector is measured by the inductive sensor. The average velocity v is estimated by

where 
The dynamics of the integral system can be regarded approximately as a second order system according to our previous research [19] [20] . As such, a second order ARX model was employed to describe the system dynamics, while the hysteresis exhibited by the actuator and the friction between the stage and the end-effector are considered as extra disturbances to the dynamic model. For the experiments, a 10 V step input reference voltage was provided to the PEA and the corresponding output velocity was estimated by Equation (23). With the recorded data, the parameters were identified by using the least square method, leading to

3.2. Step Tracking
The ARX-based PID-SMC developed in this study was implemented in experiments to control the velocity of the piezoelectric-driven slick-slip actuator. The sliding surface was defined according to Equation (9), where 
Figure 6 shows the velocity step response of the piezoelectric-driven stick-slip actuator controlled by the developed control scheme and the traditional PID controller. Table 1 shows the comparison of the rising time and the overshoot.
It can be seen that the tracking errors approach to zero through the use of I component in the PID regulator. The velocity step response of the piezoelectric-driven stick-slip actuator controlled by the proposed method is faster than that controlled by the traditional PID controller. For example, when a 10 μm/s step reference input was provided, the rising time of the velocity step response controlled by the ARX-based PID-SMC is 0.13 s, 0.2 ms less than that controlled by the PID controller. Faster velocity response is also observed for the 20 μm/s step reference input. However, since the dynamics performance of the piezoelectric-driven stick-slip actuator varies with the amplitude of the input voltage, the model error increased when the 20 μm/s step reference input was provided to the actuator. As a result, the overshoot increased to 10% in this case.
Figure 5. Reverse saw-tooth to driven the end-effector in the backward direction.
Figure 6. Velocity Step response of the piezoelectric-driven stick-slip actuator controlled by the proposed method and the traditional PID controller (a) 10 μm/s desired velocity; (b) 20 μm/s desired velocity.
Table 1. Comparison of the velocity step response between the ARX-based PID-SMC and the traditional PID controller.
To test the control performance of the proposed method, the same velocity step tracking experiments were also carried out with an increased mass of the end-effector. The same parameters is applied and compared with the traditional PID controller. Figure 7 shows the velocity step response of the piezoelectric-driven stick-slip actuator controlled by the developed control scheme and the traditional PID controller. Table 2 shows the comparison of the rising time and the overshoot. It can be concluded that the velocity step response of the piezoelectric-driven stick-slip actuator controlled by the proposed method is faster than that controlled by the traditional PID controller.
It is noted that the rising time of the velocity step response controlled by the ARX-based PID-SMC is 0.09 s. This is different from the result with an decreased mass of the end-effector, since the dynamics of the piezoelectric-driven stick-slip actuator also changes with the weight of the end-effector.
3.3. Sinusoidal Tracking
To further show the effectiveness of the proposed control method, sinusoidal tracking experiments with different
Figure 7. 10 μm/s Step response of the piezoelectric-driven stick-slip actuator controlled by the proposed method and the traditional PID controller.
Table 2. Comparison of the velocity step response between the ARX-based PID-SMC and the traditional PID controller with an increased mass of the end-effector.
frequencies were carried out on the piezoelectric-driven stick-slip actuator. The same parameters were applied and the control performance was compared with the same PID controller. Figure 8 shows the sinusoidal tracking performance of the piezoelectric-driven stick-slip actuator controlled by the proposed method and the traditional PID controller.
Table 3 compares the tracking error evaluated in terms of the 2-norm of the difference between the desired output and the measured output. From Table 3, it can be seen that the developed control scheme performs better than the traditional PID controller. As frequency increases, the priority of applying the ARX-based PID-SMC is more obvious. For example, for a 0.25 Hz 10 µm/s sinusoidal reference input, the tracking error with ARX- based PID-SMC is 1.12 µm, which is 29.7% of that with the PID controller. While for a 1 Hz sinusoidal reference input, the improvement increases to 40.2%.
It is noted that the velocity tracking performance deteriorates when the motion direction of the end-effector changes. For example, for 10 μm/s 1 Hz sinusoidal reference velocity, the maximum tracking error in time interval 0.5 - 0.75 s and 1.5 - 1.75 s is 50% of the amplitude if controlled by the ARX-based PID-SMC. The maximum tracking error even reaches 100% of the reference amplitude of the traditional PID controller is applied. This might be due to the nonlinear friction force between the end-effector and moving stage when the velocity changes from positive to negative. Obviously, the ARX-based PID-SMC partially compensates the nonlinearity. Consideration of the nonlinear friction model and its integration in the controller design are required for further improvement on the velocity tracking performance of the piezoelectric-driven stick-slip actuator.
4. Conclusion
This paper presents the development of an ARX-based PID-SMC for the velocity control of the piezoelectric- driven stick-slip actuator. Specifically, by applying ARX model, the output-tracking problem is defined as one of state tracking, while the “bang-bang” switching control in SMC is replaced with PID-based one. With the developed control scheme, chattering or the state oscillation at a high frequency can be eliminated and also the zero steady state error can be achieved. To verify the effectiveness of the developed control scheme, experiments were carried out on a piezoelectric-driven stick-slip actuator, whose dynamics was identified by experiments. The results of velocity tracking performance with the proposed control scheme were compared to that with the traditional PID controller. It was shown that both the step response and the sinusoidal tracking performance can be further improved by applying the proposed method, although the ARX model error exists. Howev-
Table 3. Comparison of the velocity step response between the ARX-based PID-SMC and the traditional PID controller with an increased mass of the end-effector.
Figure 8. Comparison of sinusoidal tracking performance with different controllers: displacement and tracking error for (a) (b) 0.25 Hz frequency, (c) (d) 0.5 Hz frequency and (e) (f) 1 Hz frequency.
er, the control performance of the ARX-based PID-SMC depends on the accuracy of the identified dynamic model. This might be solved by employing a dynamic model with adaptive parameters and an adaptive ARX-based PID-SMC, which will be the focus of the future work. Furthermore, nonlinear friction model should be considered in the SMC design to further improve the velocity tracking performance of the piezoelectric-driven stick- slip actuator.
Acknowledgements
The support to the present study from the China Scholarship Council (CSC) and the Natural Sciences and Engineering Research Council (NSERC) of Canada is acknowledged.
References
- Devasia, S. and Moheimani, S.O.R. (2007) A Survey of Control Issues in Nano-Positioning. IEEE Transactions on Control System Technology, 15, 802-823. http://dx.doi.org/10.1109/TCST.2007.903345
- Shiratori, H., Takizawa, M., Irie, Y., Hirata, S. and Aoyama, H. (2012) Development of the Miniature Hemispherical Tilt Stage Driven by Stick-Slip Motion Using Piezoelectric Actuators. Mechatronics-REM, Paris, 21-23 November.
- Zhang, Q.S., Chen, X.B. Yang, Q. and Zhang, W.J. (2012) Development and Characterization of a Novel Piezoelectric-Driven Stick-Slip Actuator with Anisotropic-Friction Surfaces. International Journal of Advanced Manufacture Technology, 61, 1029-1034. http://dx.doi.org/10.1007/s00170-011-3771-y
- Eigoli, A.K. and Vossoughi, G. (2010) Dynamic Modeling of Stick-Slip Motion in a Legged Piezoelectric Driven Microrobot. International Journal of Advanced Robotic Systems, 7, 201-208.
- Kang, D. (2012) Modeling of the Piezoelectric-Driven Stick-Slip Actuators. Master Thesis, College of Graduate Studies and Research, University of Saskatchewan, Saskatoon.
- Bergander, A. and Breguet, J.M. (1998) Performance Improvement for Stick-Slip Positioners. International Symposium on Micromechatronics and Human Science, 59-66.
- Spiller, M. and Hurak, Z. (2011) Hybrid Charge Control for Stick-Slip Piezoelectric Actuators. Mechatronics, 21, 100- 108. http://dx.doi.org/10.1016/j.mechatronics.2010.09.002
- Rakotondrabe, M., Haddab, Y. and Lutz, P. (2008) Voltage/Frequency Proportional Control of Stick-Slip Micropositioning Systems. IEEE Transactions on Control System Technology, 16, 1316-1322. http://dx.doi.org/10.1109/TCST.2008.917232
- Rakotondrabe, M., Haddab, Y. and Lutz, P. (2009) Development of Modeling and Control of Mircro/Nano-Positioning 2-DOF Stick-Slip Device. IEEE Transactions on Mechatronics, 14.
- Breguet, J.M. and Clavel, R. (1998) Stick and Slip Actuators: Design, Control, Performances and Applications. International Symposium on Micromechatronics and Human Sciences, Nagoya, 25-28 November 1998, 89-95.
- Young, K.D., Utkin, V.I. and Özgüner, Ü. (1999) A Control Engineer’s Guide to Sliding Mode Control. IEEE Transactions on Control System Technology, 17, 328-342. http://dx.doi.org/10.1109/87.761053
- Edwards, C. and Spurgeon, S.K. (1998) Sliding Mode Control. Taylor & Francis Ltd, London.
- Liawa, H.C., Shirinzadeh, B. and Smith, J. (2007) Enhanced Sliding Mode Motion Tracking Control of Piezoelectric Actuators. Sensors and Actuators, A138, 194-202. http://dx.doi.org/10.1016/j.sna.2007.04.062
- Wang, S., Habibi, S., Burton, R. and Sampson, E. (2006) Sliding Mode Control of an Electrohydraulic Actuator System with Discontinuous Nonlinear Friction. Proceedings of the Institution of Mechanical Engineers, 222, Part I:J, Systems and Control Engineering.
- Peng, J.Y. and Chen, X.B. (2014) Integrated PID-Based Sliding Mode State Estimation and Control for Piezoelectric Actuators. IEEE/ASME Transactions on Mechatronics, 19, 88-99. http://dx.doi.org/10.1109/TMECH.2012.2222428
- Cao, Y. and Chen, X.B. (2014) Disturbance Observer Based Sliding Mode Control for a Three-DOF Nano-Positioning Stage. IEEE/ASME Transactions on Mechatronics, 19, 924-931. http://dx.doi.org/10.1109/TMECH.2013.2262802
- Cao, Y. and Chen, X.B. (2012) Integrated Inversion-Feedforward and PID-Based Sliding Mode Control for Piezoelectric Actuators. American Control Conference, Montreal, 27-29 June 2012.
- Peng, J.Y. and Chen, X.B. (2011) Modeling of Piezoelectric-Driven Stick-Slip Actuators. IEEE/ASME Transactions on Mechatronics, 16, 394-399. http://dx.doi.org/10.1109/TMECH.2010.2043849
- Cao, Y. and Chen, X.B. (2012) A Novel Discrete ARMA-Based Model for Piezoelectric Actuator Hysteresis. IEEE/ ASME Transactions on Mechatronics, 17, 737-744. http://dx.doi.org/10.1109/TMECH.2011.2128339
- Chen, X.B., Zhang, Q.S., Kang, D. and Zhang, W.J. (2008) On the Dynamics of Piezoelectric Positioning Systems. Review of Scientific Instrument, 79, Article ID: 116101. http://dx.doi.org/10.1063/1.2982238










