Modern Mechanical Engineering
Vol.3 No.3A(2013), Article ID:34861,8 pages DOI:10.4236/mme.2013.33A002
Vibration Control of a Gym Floor Using Tuned Mass Dampers: A Numerical Analysis
Departamento de Engenharia Civil e Ambiental, Faculdade de Tecnologia, Universidade de Brasilia, Brasilia, Brasil
Email: marcos.santos@cidades.gov.br, danielvalenca1@yahoo.com.br, georcam2003@yahoo.es, avilas@unb.br, graciela@unb.br
Copyright © 2013 Marcos Daniel Souza dos Santos et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 23, 2013; revised June 26, 2013; accepted July 7, 2013
Keywords: Structural Dynamics; Structural Control; Concrete Slabs; Tuned Mass Damper
ABSTRACT
This work presents a study on excessive vibration problem occurring on concrete slabs, usually used on residential and commercial building floors. Even well designed slabs, according to ultimate and serviceability limit states criteria, can be vulnerable to undesirable vibrations that lead to user discomfort. A gym floor, that presented real excessive vibrations, located in a commercial building situated in the city of Brasilia, Brazil, was analyzed via Finite Element Method using ANSYS software. The first step in this analysis was to obtain natural frequencies and vibration modes, the structure presented low natural frequencies representing its flexible behavior. Then it was simulated a dynamic loading of people jumping, characteristic of this type of building occupation. Since it was observed the occurrence of excessive vibrations also in the numerical analysis, a Tuned Mass Damper (TMD) control system was proposed, looking for the best set of dampers to improve the control performance. The parameters for the best vibration reduction were obtained via a parametric study considering four different slabs varying dimensions and support conditions. Different models considering one and more TMDs, varying its placements and parameters, besides the frequency reference value to tune the damper were considered. An efficient control solution to this practical problem is presented to reduce its undesirable vibrations.
1. Introduction
Human induced loads can cause excessive vibration leading to discomfort and even compromising structural safety. Real occurrences of this problem in structures subjected to loads originated from people movement are worldwide known, a famous example is the London Millenium Footbridge [1]. Floor vibration studies have intensified in the last years. A number of factors cause this effect; the more important are: the use of more resistant materials that lead to more slender and flexible slabs, and the occurrence of non-provided activities in the original structural design. Those things have contributed to increasing emergence of excessive vibration on structures, especially on slabs [2,3]. This problem is directly linked to the structural control devices study. Structural control provide changes on stiffness and damping properties of the system, installing external devices or applying external forces, aiming to reduce original structure vibrations.
Among several structural control devices there is the Tuned Mass Damper (TMD), a damper applied in many practical cases, such as high buildings, footbridges, towers, etc. [4]. It is a mass-spring-dashpot system connected to the structure in a way to vibrate out of phase with the main structure, if tuned to the appropriated frequency. In this way the energy is transferred to the TMD reducing amplitude vibration on the main system. The use of TMD to reduce floor vibration has been studied by many researchers lately [5-9]; however there are still many topics to further development, such as the determination of appropriate TMD parameters to optimize control performance. This work presents a floor vibration study to a practical case of a gym. The slab analyzed presented excessive vibration problems when subjected to typical human induced loading of rhythmic exercise practicing. A control system consisting of various TMD was proposed. This proposal was based on a parametrical study to improve the performance of a slab set with typical dimensions of structures like residential and commercial buildings.
2. Human Induced Vibrations
Nowadays the design of building floors with low natural frequencies, with values near of those from human induced loads, can cause undesirable excessive vibrations.
Thus the understanding of structural dynamic behavior and the characteristics of the dynamic load is very important, particularly to floor slabs. Dynamic loading can produce high vibration levels than can cause discomfort to users and even compromise structural safety. Occurrence’s of these problems are well known worldwide, like the already mentioned London Millenium Footbridge [1]. The stadium grandstands collapse in the 1920 years lead the American Standards Association (ASA, atual ANSI—American National Standards Institute) to nominate a committee to establish safety standards for this type of structure. Decades later, researchers described mathematically human loading arising from typical activities using a Fourier series. Faisca [10] performed an experimental study focusing on this type of load, describing human induced dynamic load considering loss of contact with the structure. According to her, these loads can change depending on structure’s flexibility, namely they depend on people-structure interaction. Varela [5] studied human induced loading correlating the mathematical model with experimental results.
3. Structural Control: Tuned Mass Damper (TMD)
Tuned Mass Damper reduces the energy dissipation request of structural members when subjected to dynamic loads. This reduction occurs by transferring a portion of the vibratory energy to the TMD that in its simplest conception is a mass-spring-dashpot system connected to the structure, like shown on Figure 1. Considering the main system like a single-degree-of-freedom model, with mass M, damping C and stiffness K, on which is applied a dynamic load f(t) and attached a TMD with mass m, damping c and stiffness k, the equations of motion are:
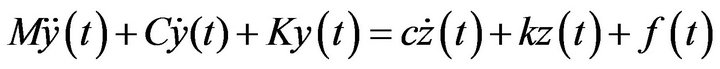 (1)
(1)
 (2)
(2)
where:
ÿ(t): main system acceleration;
y(t): main system velocity;
y(t): main system displacement;
z(t): relative displacemente between the TMD and the main system.
When installed, the TMD tries to bring resonance peaks to lower values; this effect is desirable occurring on a wide frequency range.
For this to happen, TMD optimum parameters should be obtained, improving the control system performance [11]. A large number of these devices have been installed in high buildings, bridges, towers and industrial chimneys to control the dynamic response due to strong winds mostly [2]. In recent years studies were developed to
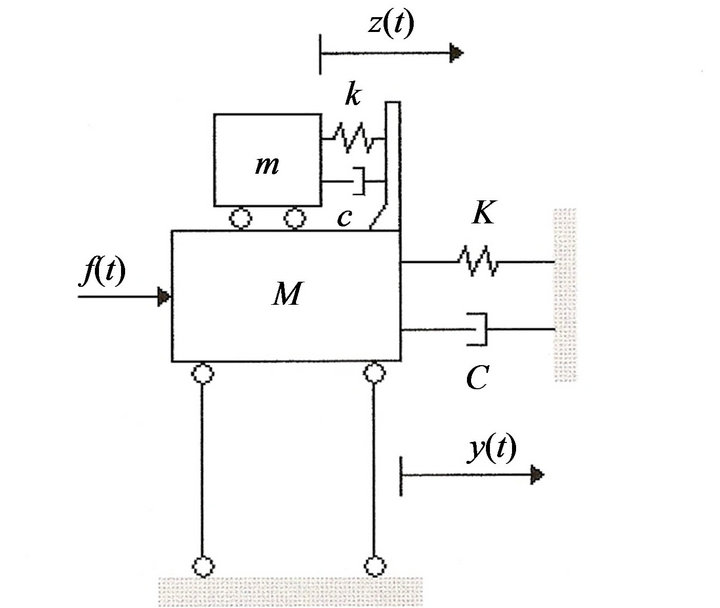
Figure 1. Structural system model with a TMD installed [4].
harness the potential of TMD on floor vibration control. Battista & Varella [12] presented a practical case of using TMDs in commercial building with metallic beams and composite floor decks that presented excessive vibration levels according to ISO 2631/1, ISO 2631/2 and NBR 8800 ABNT codes. Setareh et al. [8] describe the application of a passive pendulum working as a TMD for two cases with excessive slab vibrations. In this study they emphasize men-structure interaction on experimental results obtained.
4. TMD Parametric Study
The four slab structures studied in this work are shown in Figure 2. The loading applied simulated people on the move.In all cases analyzed it was verified vibration levels higher than those recommended on standard codes. Thus it was performed a study analyzing different TMD configurations in a way to verify the best control proposal for each one of the slabs. This study also analyzed the influence of TMD parameters on the control strategy performance. Because of the absence of design criteria to set parameters to TMD installed on floors, it was performed a parametrical study varying the mass ratio μ, the frequency ratio α and the damping ratio ξ, and verifying for each set of parameters the TMD efficiency. The four models presented natural frequencies near of values that characterize human dynamic loads. On the first slab studied, simply supported at the four edges, the best configuration obtained was a single TMD placed at the midspan, it reduced on 75% displacement amplitude.
Table 1 presents the bests reductions for each slab, applying harmonic loading and human-induced loading, associated frequency ratios are also presented. It can be verified that best reductions were obtained considering the theoretical harmonic loading compared to human-induced loading. In the case of Slab 1, the best verified value of α was 0.95, namely tuning the TMD very close to the corresponding slab natural frequency. For damping ratio it was concluded that increasing its value can worsen TMD
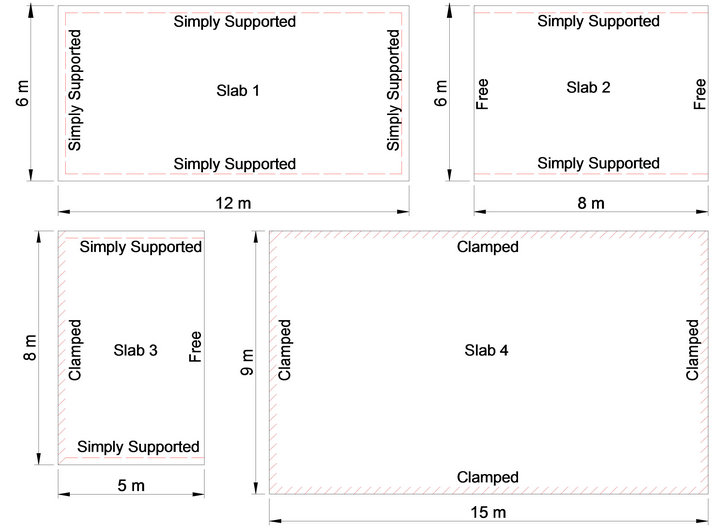
Figure 2. Dimensions and support conditions of the four slab models analyzed.
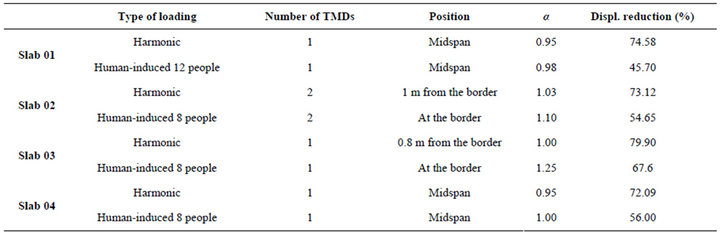
Table 1. Parametrical study results: frequency ratio and displacement reduction.
performance. The more increase applied to mass ratio, best is the efficiency. However, this parameter requires special attention because the damper weight increase can lead to excessive static deformations, compromising structural safety. The parametric studies performed allowed to observe the influence of the frequency ratio (α) change in the displacement reducing, shown in Figure 3, as well as mass ratio (μ) and damping ratio influence (ξ), represented on Figures 4 and 5. Similar studies were performed by in the other slabs shown in Figure 2, they are well detailed on the work of Santos [13]. Numerical simulations indicated that the parameter which design should be more careful, since it has a great influence on final results, is the frequency ratio α. Damping ratio ξ and mass ratio μ didn’t show the same influence.
5. Analysis of a Gym Slab
A gym floor, that presented excessive vibrations, located in a commercial building situated in the city of Brasilia, Brazil, was analyzed via Finite Element Method using ANSYS software. The commercial building has five floors: a basement, downstairs, first and second floor and roof. All floors were built as concrete solid slabs with 15 MP a resistance, 7 cm of thickness, supported by beams and columns of rectangular section.
A rectangular portion of the floor situated in downstairs floor with 14.074 m × 6.49 m and 3.15 m of height, showed on Figure 6 was considered here. In this sector of the floor is located the ballroom gymnastics. The physical properties attributed to the numerical model
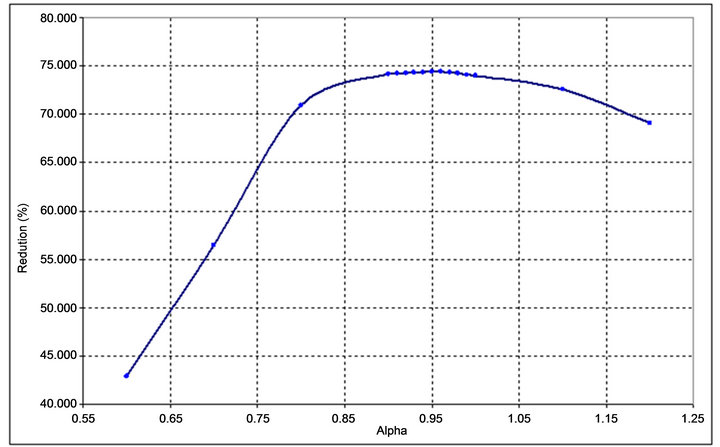
Figure 3. Frequency ratio α influence on displacement reduction (μ = 0.10 and ξ = 0.40) Slab 1.
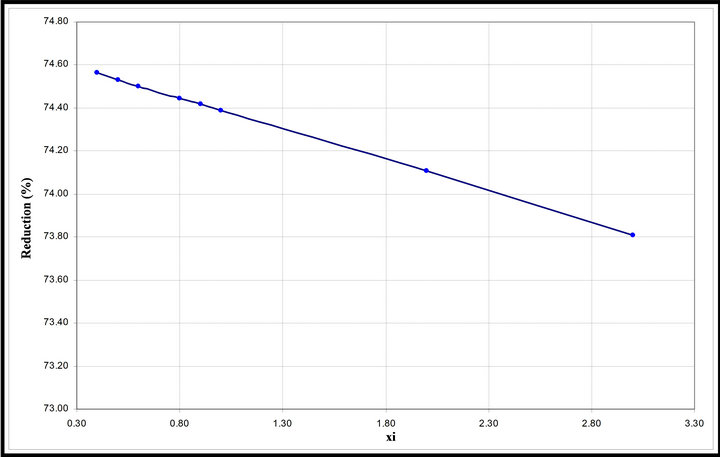
Figure 4. Damping ratio ξ influence on displacement reduction (μ = 0.10 and α = 0.96) Slab 1.
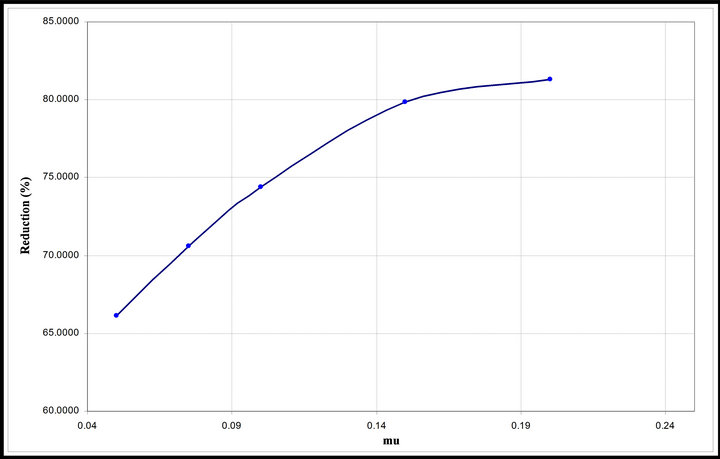
Figure 5. Mass ratio influence μ on displacement reduction (ξ = 0.4 and α = 0.96) Slab 1.
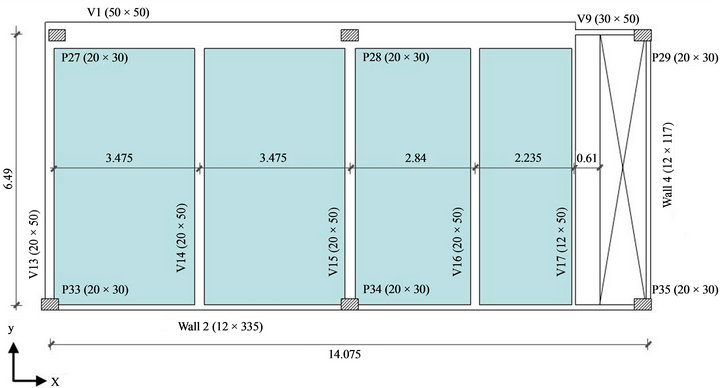
Figure 6. Dimensions and structural sketch of the gym floor portion studied.
were: Modulus of Elasticity of 29 Gpa; density of 2500 kg/m3 and Poisson ratio of 0.3. The studied slab was modeled with a finite element mesh in the XY plane, using SHELL63 elements. Beams were modeled using BEAM4, as well as columns.
Modal analysis showed natural frequencies values near of those from human induced loads. The first three mode shapes are in the horizontal direction with bending of the columns in the first mode and column bending and torsion in the second and third modes. From the fourth mode arise vertical displacements on the structure [13]. A transient analysis was also performed simulating the loading of people jumping. Nineteen people were considered placed at a distance of 1.0 m between one another, covering all the slab area.
Table 2 present the maximum response value on the node where it was verified the largest vertical displacement on the transient analysis of nineteen people jumping.
To attenuate these excessive vibrations it was proposed a control strategy using TMDs. In the absence of design TMD criteria, initially Jangid and Den Hartog [4,14] parameters were considered. It is noteworthy that these above parametric suggestions were based on different type of structures like single-degree-of-freedom model and shear buildings. The best performance was achieved using 6 TMD where three of them were tuned to the first natural frequency (2.56 Hz) and working on Y direction (horizontal) and the other ones tuned in the fourth natural frequency (9.35 Hz) and working on Z direction (vertical). The Z directions dampers were placed individually on the midspan of beams V14, V15 and V16. The Z direction dampers were located in the midspan of the three slabs; these nodes presented the largest displacements in the analysis. However, those were not good results, since it was achieved a 20% acceleration reduction, but also a 10% increase on displacements.
Therefore, a new analysis, based on the parametric studies presented earlier in this work, was performed.The nodes chosen to attach the TMDs were the slab’s midspan nodes, which presented the largest displacement amplitudes. Three proposals with different numbers of TMDs were studied (1, 2 and 3 dampers). The best proposal showed to be the one using a single TMD.
The TMD was placed on the node in the slab midspan between beams V13 and V14, as shown in Figure 7. The adopted TMD parameters were a = 0.96; m = 0.10 and x = 0.4. The TMD was tuned to the first and fourth frequencies (A1 and A2 models) as shown on Table 3. Maximum responses are presented on Table 4. Model

Table 2. Uncontrolled largest node response.
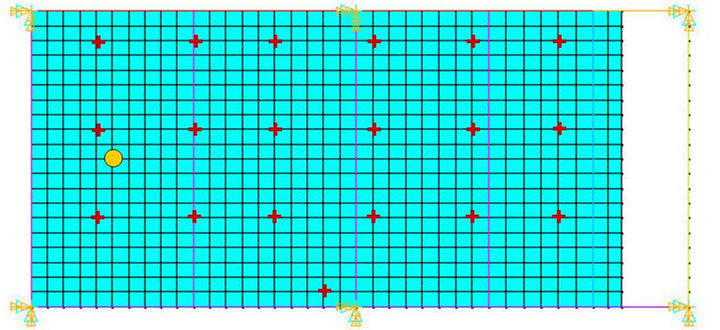
Figure 7. Gym slab with TMD installed on node 386, better position to vibration reduction.

Table 3. TMD properties to models A1 and A2.

Table 4. Maximum displacements, accelerations and correspondigreductionr to A1 and A2 models.

Table 5. TMD properties to models A3 and A4.

Table 6. Maximum displacements, accelerations and corresponding reductions to A3 and A4 models.

Table 7. Comparative results of displacements and accelerations.
A1 was the better alternative with a 10.449% displacement reduction and a 12.995% acceleration reduction. Despite presenting a greater acceleration reduction, model A2 presented displacement amplification.
Still considering a single TMD placed at the same node, a new set of parameters was attributed based on work of Santos [13] parametric studies of a 3D model considering beams and columns, similar to the present work structure. The parameter values adopted were α = 0.82, m = 0.10 and x = 0.4, as indicated on Table 5, where A3 is the model tuning the TMD on the first frequency and A4 the TMD tuned on the fourth frequency. The dynamic response in both cases is presented on Table 6.
It is verified that, as well as in the last proposal, a better performance with the TMD tuned on the first frequency presenting a 7.514% displacement reduction and a 9.881% acceleration reduction. Nevertheless, model A1 showed better performance.
Based on all presented results it can be concluded that the displacement reduction is better achieved tuning the TMD to the first frequency. In acceleration reduction the best performance happened when tuning the TMD to the fourth frequency, but in these cases an undesirable increase on displacements was observed. In this way, the best proposal to control the structure is model A1, using a single TMD tuned to the first natural frequency of the structure. A comparison between model A1 and the 6 TMD initial proposal is shown in Table 7. Model A1 was the more indicated design in a way that despite not reducing so well accelerations, no increase in displacement is noticed. A displacement increase is not recommendable in a structural point of view.
6. Conclusion
This paper presents the study of the vibration problem of a commercial building floor used as a gym. The concrete slab analyzed presented excessive vibrations when subjected to typical exercise rhythmic loading. A control system was proposed using the Tuned Mass Damper device. Also a parametric study to design the TMD was performed considering four different concrete slabs with varying dimensions, support conditions and loads. The control system showed to be effective reducing by 10% displacement amplitudes of the gym floor analyzed.
7. Acknowledgements
This work has been supported by CNPq and CAPES brazilian agencies which are gratefully acknowledged.
REFERENCES
- P. Dallard, A. I. Fitzpatrick, A. Flint, S. Le Bourva, A. Low, R. Smith and M. R. Willford, “The London Millennium Footbridge,” The Structural Engineer, Vol. 79, No. 22, 2001, pp. 17-33.
- I. Saidi, “Development of a Viscoelastic Tuned Mass Damper to Reduce Walking Induced Vibrations in Building Floors,” Thesis of Doctor of Philosophy, Swinburne University of Technology, Melbourne, 2012.
- J. E. Campuzano, R. Castro, S. M. Avila and G. Doz, “Platform for Dynamic Tests: Preliminary Studies, Design and Construction,” RevistaIbracon de Estruturas e Materiais, Vol. 6, No. 1, 2013, pp. 55-74. doi:10.1590/S1983-41952013000100004
- T. T. Soong, G. F. Dargush, “Passive Energy Dissipation in Structural Engineering,” John Wiley & Sons, Chichester, 1997.
- W. D. Varela, “Modelo Teórico Experimental para Aná- lise de Vibrações Induzidas por Pessoas Caminhando Sobre Lajes de Edifícios,” Ph.D. Thesis, COPPE/UFRJ, Rio de Janeiro, 2004.
- D. V. F. Lima, “Controle de Vibrações Induzidas em uma Laje de Academia de Ginástica com a Utilização de Amortecedores de Massa Sintonizados,” Master Thesis, Universidade de Brasília, Brasília, 2007.
- M. Setareh, J. K. Ritchey, A. J. Baxter and T. M. Murray, “Pendulum Tuned Mass Dampers for Floor Vibration Controll,” Journal of Performance of Constructed Facilities, ASCE, Vol. 20, No. 1, 2006, pp. 64-73. doi:10.1061/(ASCE)0887-3828(2006)20:1(64)
- M. Setareh, J. K. Ritchey, T. M. Murray, J. H. Koo and M. Ahmadian, “Semiactive Tuned Mass Dampers for Floor Vibration Control,” Journal of Structural Engineering, ASCE, Vol. 133, 2007, pp. 242-250.
- W. D. Varela and R. C. Battista, “Control of Vibration Induced by People Walking on Large Span Composite Floor Decks,” Engineering Structures, Vol. 33, No. 9, 2011, pp. 2485-2494. doi:10.1016/j.engstruct.2011.04.021
- R. G. Faisca, “Caracterização de Cargas Dinâmicas Geradas por Atividades Humanas,” Ph.D. Thesis, COPPE/ UFRJ, Rio de Janeiro, 2003.
- S. M. Avila, “Controle Híbrido para Atenuação de Vibra- ções em Edifícios,” Ph.D. Thesis, Pontifícia Universidade Católica do Rio de Janeiro, Rio de Janeiro, 2002.
- R. C. Battista and W. D. Varela, “Medidas Corretivas para Vibrações de Painéis Contínuos de Lajes de Edifícios,” Proceedings of the 30th Jornadas Sul-Americanas de Engenharia Estrutural, Brasilia, 2002.
- M. D. S. Santos, “Análise Numérica Do Controle de Vibrações em Lajes de Edifícios Utilizando Amortecedores de Massa Sintonizados,” Master Thesis, Universidade de Brasília, Brasília, 2009.
- R. Jangid, “Optimum Multiple Tuned Mass Dampers for Base Excited Undamped System,” Earthquake Engineering and Structural Dynamics, Vol. 28, No. 9, 1999, pp. 1041-1049. doi:10.1002/(SICI)1096-9845(199909)28:9<1041::AID-EQE853>3.0.CO;2-E

