Modern Mechanical Engineering
Vol.2 No.4(2012), Article ID:24886,4 pages DOI:10.4236/mme.2012.24016
Study on MHD Viscous Flow over a Stretching Sheet Using DTM-Pade’ Technique
Department of Mechanical Engineering, Babol University of Technology, Babol, Iran
Email: m_r_azimi1991@yahoo.com
Received July 4, 2012; revised August 9, 2012; accepted August 22, 2012
Keywords: MHD Viscous Flow; Stretching Sheet; Differential Transformation Method; Pade Approximant
ABSTRACT
In this paper, we present the study of momentum characteristics in a MHD viscous flow over a stretching sheet. First the partial differential equations of motion have been transformed to an ordinary differential equation. The analytical method called Differential Transformation Method (DTM) powered by the Pade’ approximation is applied to solve the nonlinear equation derived from MHD viscous flow over a stretching sheet, the effect of parameters variation has been investigated for two numerical cases and finally the analytical results have been compared with numerical one in a numerical case. The obtained results approve its efficiencies and capabilities beside numerical solutions achieved from Runge Kutta method.
1. Introduction
Investigations of boundary layer flow of viscous fluids over a stretching sheet are important in many manufacturing processes such as polymer extrusion, drawing of copper wires, continuous stretching of plastic films and artificial fibers, glass-fiber, metal extrusion and metal spinning. The viscous flow due to stretching boundary is important in extrusion processes where sheet material is pulled out of an orifice with increasing velocity [1].
Another area in which the theoretical study may be of interest is in the motion of liquid metals or alloys in the cooling systems. The properties of the end product depend considerably on the rate of cooling. By drawing such a sheet in a viscoelastic electrically conducting fluid subject to the action of a magnetic field, the rate of cooling can be controlled and the final product can be obtained with desired characteristics [2].
MHD viscous fluid flow was the main purpose of many pervious researches [3,4].
Most scientific problems in fluid mechanics such as MHD viscous fluid flow over the stretching sheet are inherently nonlinear by nature, and, except for a limited number of cases, most of them do not have exact solutions. Accordingly, the nonlinear equations are usually solved using other methods including numerical techniques or by using analytical method. Some of these methods are Homotopy Perturbation Method (HPM) [5-7], Differential Transformation Method (DTM) [8], Variational Iteration Method (VIM) [9] and Adomian Decomposition Method (ADM) [10,11].
The aim of this study is to discuss the analytic solutions of the two-demensional MHD viscous fluid past a shrinking sheet. Here, Differential Transformation Method (DTM) powered by pade’ approximant is used to obtain analytical solutions of the governing nonlinear differential equations. The results will be discussed in some numerical cases.
2. Problem Description
Let us consider the steady two-dimensional MHD flow of an incompressible viscous fluid over a nonlinear porous shrinking sheet at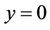 . The fluid is electrically conducted under the influence of an applied magnetic field
. The fluid is electrically conducted under the influence of an applied magnetic field 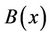 normal to the stretching sheet. The induced magnetic field is neglected. The resulting boundary layer equations are as following form:
normal to the stretching sheet. The induced magnetic field is neglected. The resulting boundary layer equations are as following form:
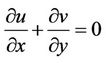 (1)
(1)
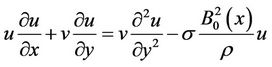 (2)
(2)
where u and v are the velocity components in the x and y directions, respectively. Also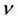 ,
,  and
and 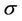 are the kinematic viscosity, density and electrical conductivity of the fluid. In Equation (2), the external electric field and the polarization effects are negligible, and:
are the kinematic viscosity, density and electrical conductivity of the fluid. In Equation (2), the external electric field and the polarization effects are negligible, and:
 (3)
(3)
The boundary conditions corresponding to the nonlinear stretching of a sheet are
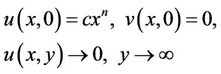 (4)
(4)
In order to solve the problem, momentum and energy equations are firstly nondimensionalized by using the following similarity variables:
 (5)
(5)
Equations (1)-(4) are transformed to
 (5)
(5)
With following boundary conditions:
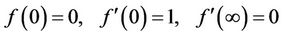 (6)
(6)
where
 (7)
(7)
3. Basic Idea
Let  be analytic in a domain D and let
be analytic in a domain D and let  represent any point in D. The function
represent any point in D. The function  is then represented by one power series whose center is located at
is then represented by one power series whose center is located at . The Taylor series expansion function of
. The Taylor series expansion function of  is in the form of:
is in the form of:
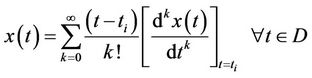 (8)
(8)
The differential transformation of the function  is defined as follows [8]:
is defined as follows [8]:
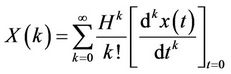 (9)
(9)
where 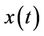 is the original function and
is the original function and  is the transformed function. The differential inverse transform of
is the transformed function. The differential inverse transform of  is defined as follows:
is defined as follows:
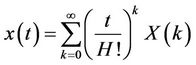 (10)
(10)
Mathematical operations performed by DTM are listed in Table 1.
Power series are not useful for large values of , say
, say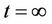 . The combination of the analytical methods with the Pade’ approximation provides a powerful tool for
. The combination of the analytical methods with the Pade’ approximation provides a powerful tool for

Table 1. Some of the basic operations of DTM.
handling boundary value problems on infinite domains. In this study we evaluate pade’ approximation using Maple software.
4. Application
In order to solve Equation (7), we consider the following boundary conditions:
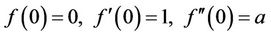 (11)
(11)
where, a should be determined.
Taking differential transform of Equation (7) by using the related definitions in Table 1, we obtain:
 (12)
(12)
As mentioned before in Equation (13), we can write:
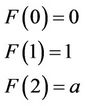 (13)
(13)
We can easily yield:
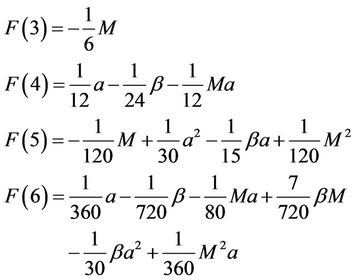 (14)
(14)
We avoid listing the other components. However it can be yielded that the closed form of the solutions is:
 (15)
(15)
Consider boundary condition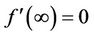 , the coefficient of the highest power of t requires being zero. Therefore a can be easily yielded.
, the coefficient of the highest power of t requires being zero. Therefore a can be easily yielded.
5. Results and Discussions
In this section, we illustrate the results in the following figure:
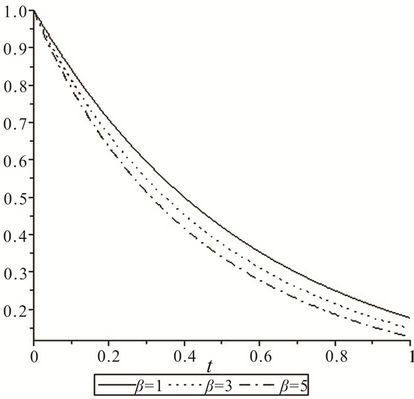
Considering the results, it can be pointed out that, as the parameters of M and β increase, the velocity components (y-direction and x-direction) descend over the stretching sheet.
In spite of the fact that both parameters are involved in reducing the velocity but it is obvious that parameter of M is more effective in this reduction rather than parameter of β, it is shown in Figure 1.
In Figure 2, the comparison between analytical results
 (a)
(a)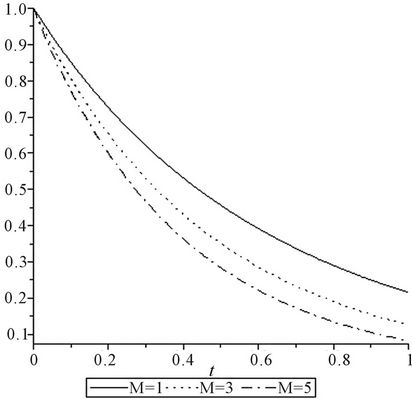 (b)
(b)
Figure 1. (a) Velocity in y-direction for M = 2, β = 1, 3, 5; (b) Velocity in y-direction for M = 1, 3, 5, β = 2.
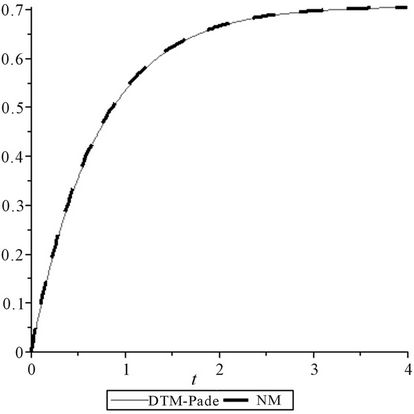
Figure 2. Comparison between analytical result and numerical solution for M = 1, β = 1.
and numerical solutions has been presented for M = 1, β = 1. As it can be illustrated that the analytical results achieved by DTM-Pade’ Technique have good agreement with numerical one obtained from forth order Runge Kutta method.
6. Conclusion
In this paper, we studied the MHD viscous flow that is conducted with an applied magnetic field. Here, Differential Transformation Method (DTM) is applied to solve the governing nonlinear differential equation with analytical solution. The results indicate that the velocity will be reduced by increasing the two parameters of M and β; however, we know that the influence of “M” in reduction of the velocity components is more than “β”. Therefore, it can be concluded that DTM is one of the best methods that let us study on MHD viscous flow analytically and get the appropriate results.
REFERENCES
- T. C. Chaim, “Hydromagnetic flow over a surface stretching with a power law velocity,” International Journal of Engineering Science, Vol. 33, No. 3, 1995, pp. 429-435. Hdoi:10.1016/0020-7225(94)00066-S
- B. Raftari and K. Vajravel, “Homotopy Analysis Method for MHD Viscoelastic Fluid Flow and Heat Transfer in a Channel with a Stretching Wall,” Communications in Nonlinear Science and Numerical Simulation, Vol. 17, No. 11, 2012, pp. 4149-4162. Hdoi:10.1016/j.cnsns.2012.01.032
- W. F. Hughes and R. A. Elco, “Magneto Hydro Dynamic Lubrication Flow between Parallel Rotating Disks,” Journal of Fluid Mechanics, Vol. 13, No. 1, 1996, pp. 21- 32. Hdoi:10.1017/S0022112062000464
- M. Siddiqui and S. Irum, A. R. Ansari, “Unsteady Squeezing Flow of a Viscous MHD Fluid between Parallel Plates: A Solution Using the Homotopy Perturbation Method,” Mathematical Modelling and Analysis, Vol. 13, No. 4, 2008, pp. 565-576. Hdoi:10.3846/1392-6292.2008.13.565-576
- D. D. Ganji and A. Rajabi, “Assessment of HomotopyPerturbation and Perturbation Methods in Heat Radiation Equations,” International Communications in Heat and Mass Transfer, Vol. 33, No. 3, 2006, pp. 391-400. Hdoi:10.1016/j.icheatmasstransfer.2005.11.001
- F. Shakeri, D. D. Ganji and M. Azimi, “Application of HPM-Pade’ Technique to a Jeffery-Hamel Flow Problem,” International Review of Mechanical Engineering, Vol. 6, No. 3, 2012, pp. 537-540.
- M. Turkyilmazoglu, “Numerical and Analytical Solutions for the Flow and Heat Transfer Near the Equator of an MHD Boundary Layer over a Porous Rotating Sphere,” International Journal of Thermal Sciences, Vol. 50, No. 5, 2011, pp. 831-842. Hdoi:10.1016/j.ijthermalsci.2010.12.014
- M. M. Rashidi, “The Modified Differential Transform Method for Solving MHD Boundary-Layer Equations,” Computer Physics Communications, Vol. 180, No. 11, 2009, pp. 2210-2217.
- J. H. He, “Variational Iteration Method for Autonomous Ordinary Differential Systems,” Applied Mathematics and Computation, Vol. 114, No. 2-3, 2000, pp. 115-123. Hdoi:10.1016/S0096-3003(99)00104-6
- G. Adomian, “A Review of the Decomposition Method in Applied Mathematics,” Journal of Mathematical Analysis and Applications, Vol. 135, No. 2, 1988, pp. 501-544. Hdoi:10.1016/0022-247X(88)90170-9
- T. Hayat, Q. Hussain and T. Javed, “The Modified Decomposition Method and Padé Approximants for the MHD Flow over a Non-Linear Stretching Sheet,” Nonlinear Analysis: Real World Applications, Vol. 10, No. 2, 2009, pp. 966-973. Hdoi:10.1016/j.nonrwa.2007.11.020

