Modern Mechanical Engineering
Vol. 2 No. 3 (2012) , Article ID: 22178 , 6 pages DOI:10.4236/mme.2012.23009
A New Differential Operator Method to Study the Mechanical Vibration
1Shandong Iron and Steel Company Ltd., Jinan, China
2Department of Mathematical Sciences, Yeshiva University, New York, USA
3The State Key Laboratory of Tribology, Tsinghua University, Beijing, China
4Department of Mathematical Sciences, Yeshiva University, New York, USA
Email: jiquansheng1@163.com, xiji@yu.edu, jilh@tsinghua.edu.cn, yzheng1@yu.edu
Received February 17, 2012; revised March 23, 2012; accepted March 31, 2012
Keywords: New Differential Operator Method; Mechanical Vibration (Torsional Vibration of Rolling-Mill); Torque Amplification Factor; Model Analysis Method; Laplace Transform
ABSTRACT
In this paper, we propose a unified differential operator method to study mechanical vibrations, solving inhomogeneous linear ordinary differential equations with constant coefficients. The main advantage of this new method is that the differential operator D in the numerator of the fraction has no effect on input functions (i.e., the derivative operation is removed) because we take the fraction as a whole part in the partial fraction expansion. The method in various variants is widely implemented in related fields in mechanics and engineering. We also point out that the same mistakes in the differential operator method are found in the related references [1-4].
1. Introduction
A very serious equipment accident occurred in 1982 in a certain factory in the iron and steel industry in Jinan, China, where the safety pin of the middle plate of a three-roll mill for mechanical protection was not broken, but the main reducer (2800 kw, center distance 1900 mm) was so damaged that the whole gear produced crack with six connection bolts whose diameter is 64 mm of highspeed side pulled off, resulting in that the production had been halted for more than 20 days, and leading to huge economic losses. In the analysis of such serious equipment accident, we employed differential operator method in [3], Laplace transform and modal analysis method to calculate the natural frequency of torsional vibration and torque amplification factor for the main transmission system in medium plate rolling-mill. It was surprising that some mistakes were found in the solutions to the dynamic resonance of the above system through differential operator method, which was inconsistent with the correct results by Laplace transform and modal analysis method. Having compared with Laplace transform, we proposed a new differential operator method and solved the above same problem, obtaining the correct results completely consistent with modal analysis method and Laplace transform. We thus solved the disastrous equipment accident with little time. Here we illustrate the new differential operator method as follows: that differential operator D of numerator part in the fraction has no effect on input function because we do not need derivative operation working on input function. However, the fraction is taken as a whole part, using partial fraction expansion. Here we apply the related property of D operator in [5,6]. In [5], there is strict mathematical foundation for the partial fraction expansion of D operator. Finally, we obtain particular solution and general solution based on Cramer’s rule as well as initial conditions. This method is suitable and powerful for solutions to different governing equations in many related vibration problems in the mechanics and engineering fields, showing more flexibility and superiority to other methods. It has not only enriched analytic methods in mechanical dynamics but also made contributions to the dynamic analysis in metallurgical equipments, where it was originally reported in [7]. Currently, in general teaching references in [1,2], for constant coefficients differential equations, the differential operator D in numerator part in its fraction affects input function through derivative operation and gives rise to errors herein.
2. The New Differential Operator Method
Without loss of generality, we introduce the new differential operator method via the rectal serial five masses torsional vibration system, see Figure 1, which is simplified in Figure 2 in the transmission system in the above original accident in 1982 we mentioned, assuming initial conditions are zero (i.e., we suppose initial displacement and initial velocity as zero, and as a general description for initial conditions, see [8]). We state the related parameters as follows:
1) Motor (2800 kW); 2) Gear coupling; 3) Flywheel; 4) Main reducer(center distance 1900 mm); 5) Safety pin coupling; 6) Herringbone gear stand; 7) Universal joint; 8) Top roller; 9) Medium roller; 10) Steel plate; 11) Lower roller.
ji(i = 1, 2, 3, 4, 5): Moment of inertia;
kij(i,= 1, 2, 3, 4;j=2,3,4,5): Torsional elastic coefficient of every axial segment (rigidity);
φi (i = 1, 2, 3, 4, 5): Angular position;
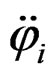 (i = 1, 2, 3, 4, 5): Angular acceleration;
(i = 1, 2, 3, 4, 5): Angular acceleration;
Mij(i,= 1, 2, 3, 4; j = 2, 3, 4, 5): Torque of every axial segment;
M: Excitation torque;
D: Differential operator on behalf of ;
;
Without the viscosity and damping, we set up the governing equations in the system:
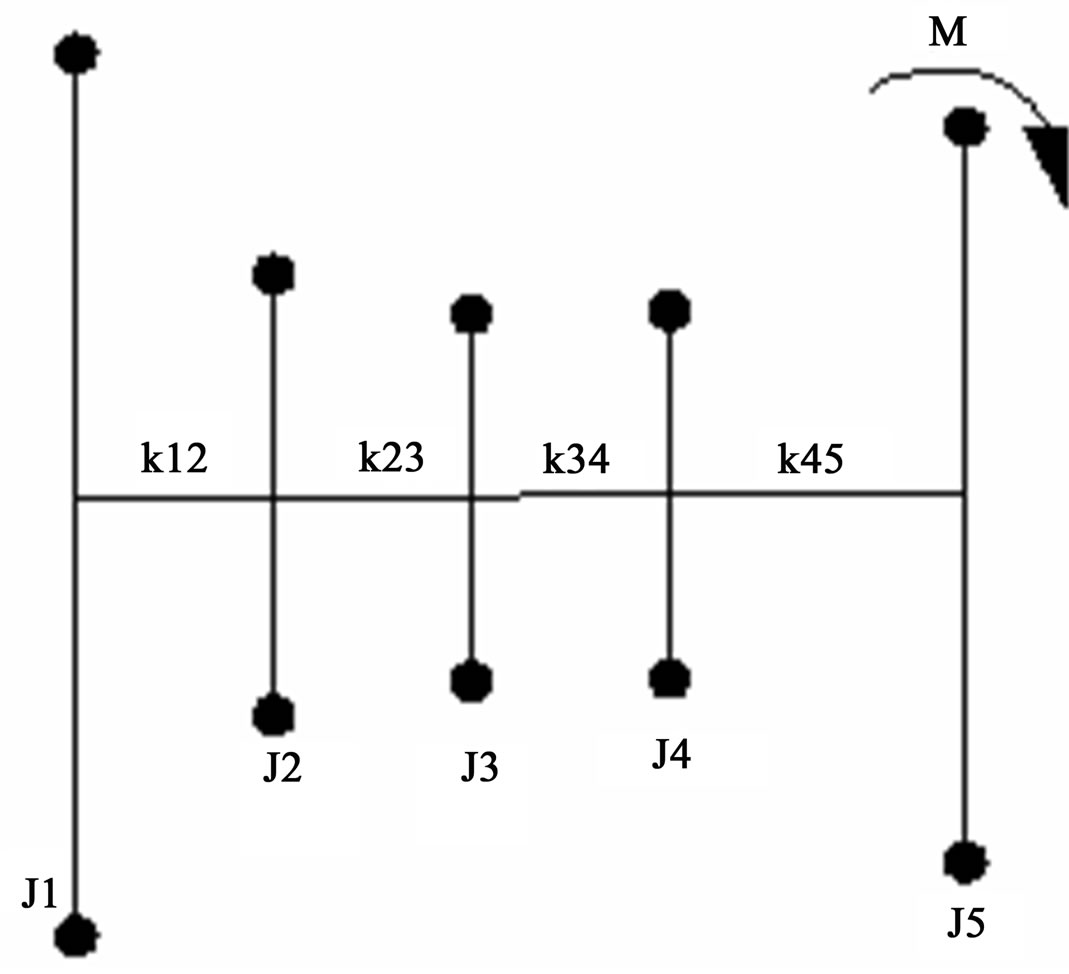
Figure 1. Diagram of five straight string masses system.
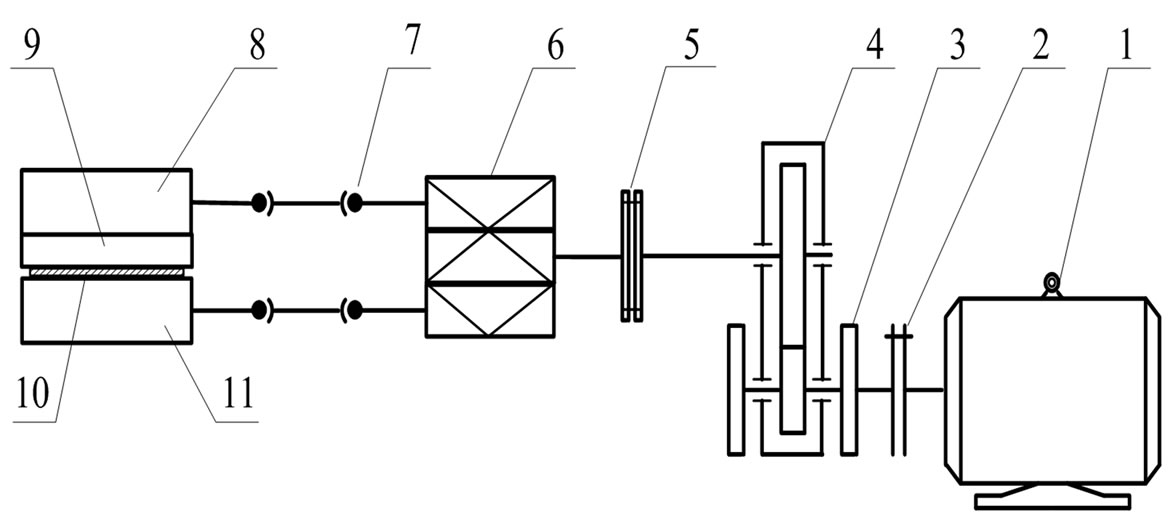
Figure 2. Diagram of transmission system.
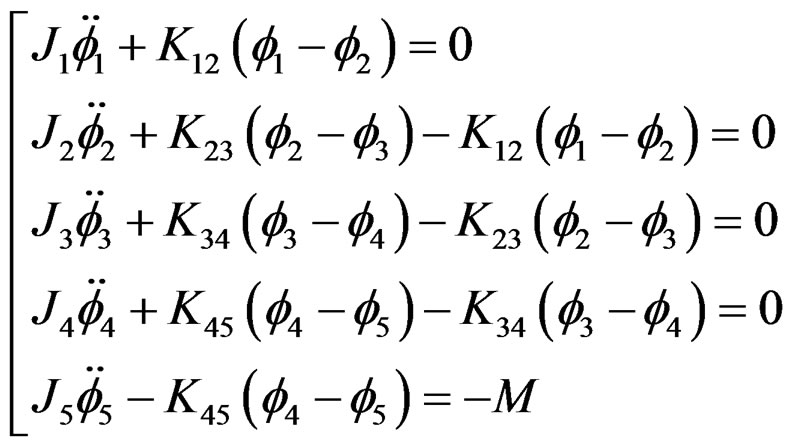 (2.1)
(2.1)
Let 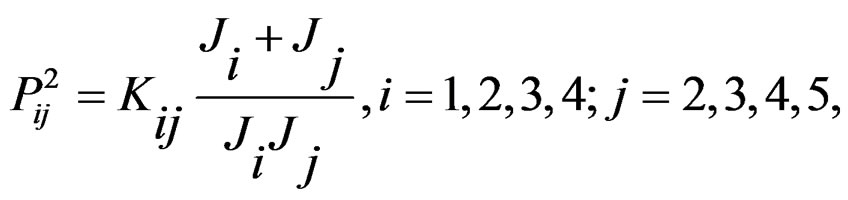
and
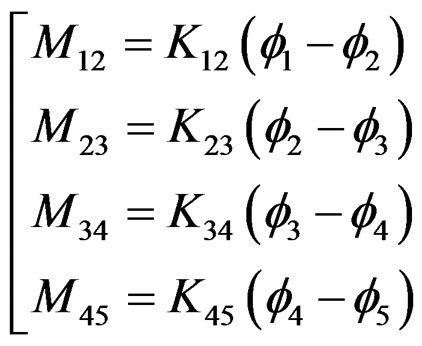 (2.2)
(2.2)
Then
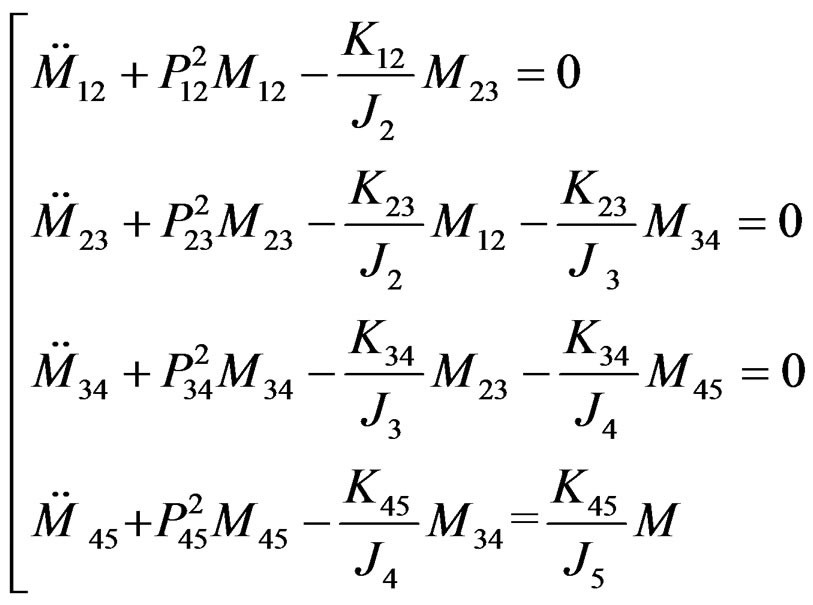 (2.3)
(2.3)
And
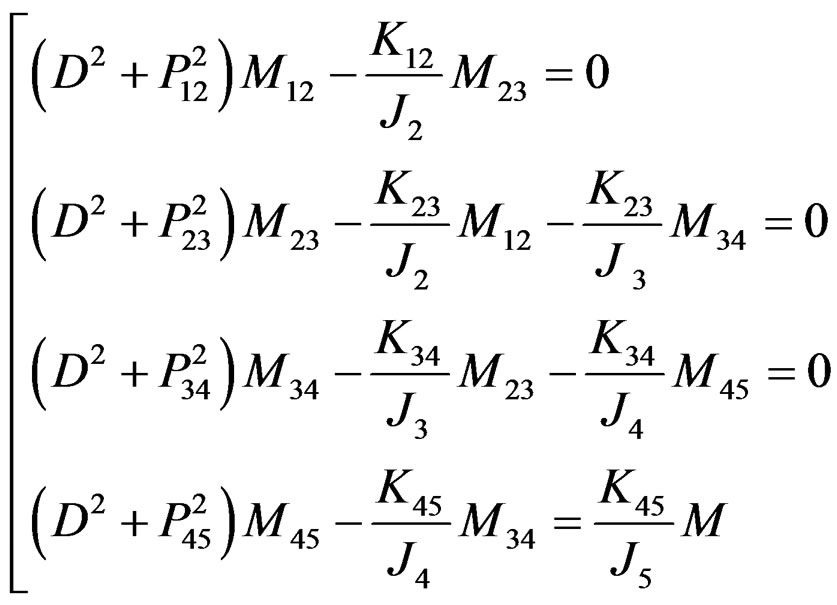 (2.4)
(2.4)
Let the determinant of the coefficient of (2.4) be Δ. Then
 where
where 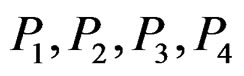 are from the first order to the fourth order natural frequencies in the main transmission system.
are from the first order to the fourth order natural frequencies in the main transmission system.
By Cramer’s rule, we calculate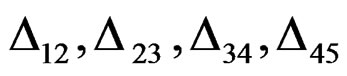 , where
, where
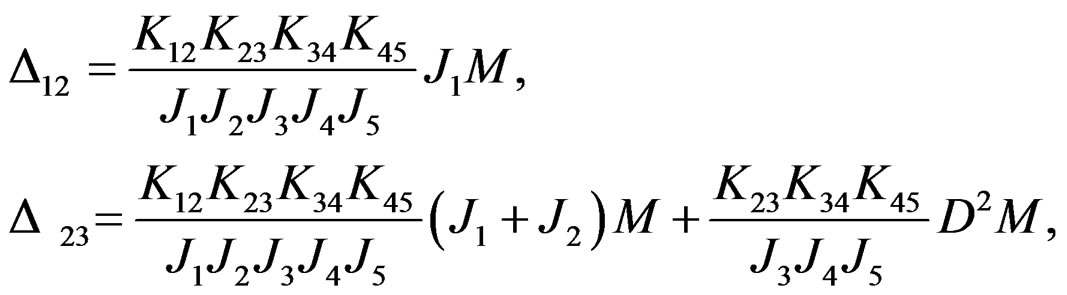
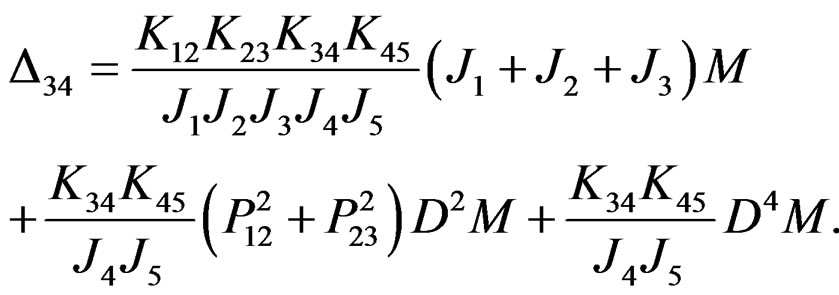
and similarly, we obtain .
.
We must pay attention to that we just take differential operator D as an algebra symbol, so it has no effect on input function, that is to say, we need not derivative operation, and we take the fraction with differential operator D in numerator and denominator as a whole part in partial fraction expansion. If we assume initial conditions of the system are zero and M is a step function, we can obtain analytic formulae of each axial segment torque individually below:

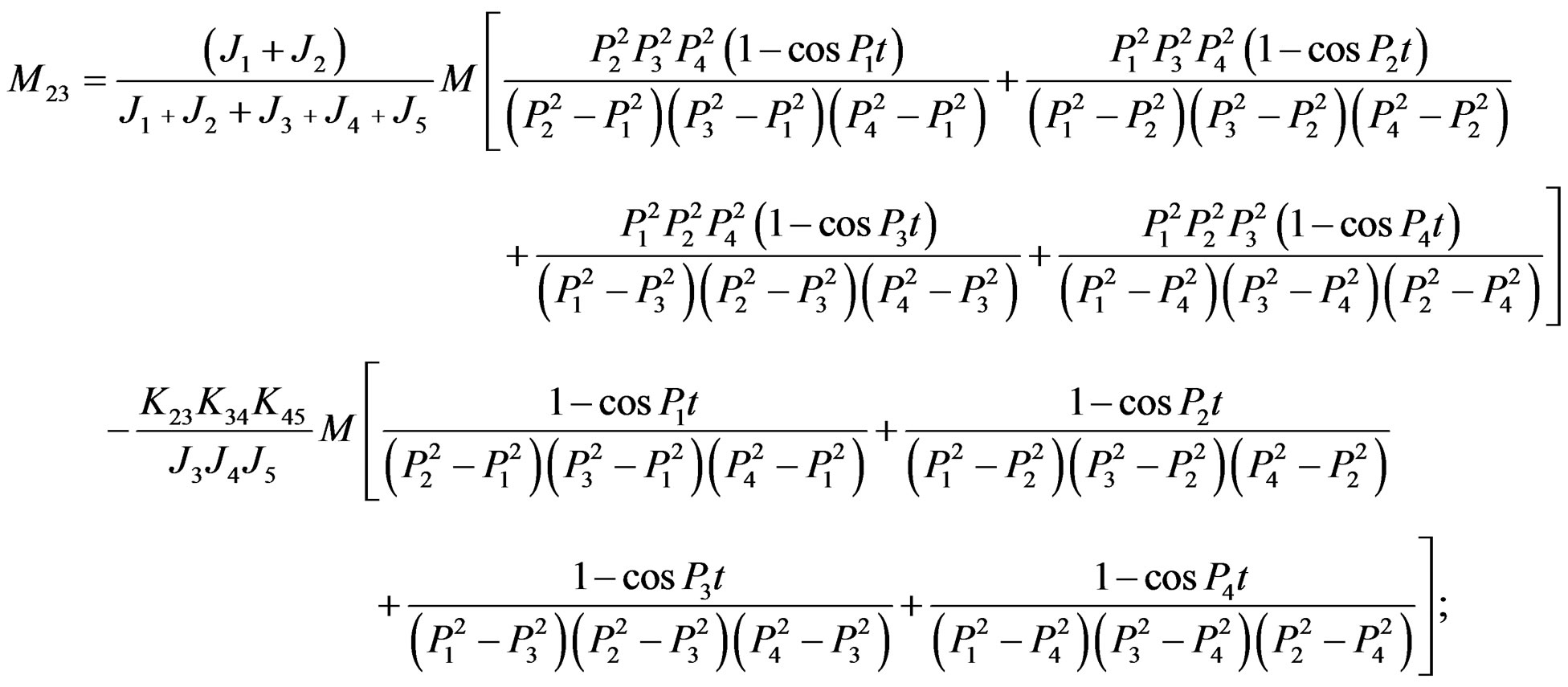
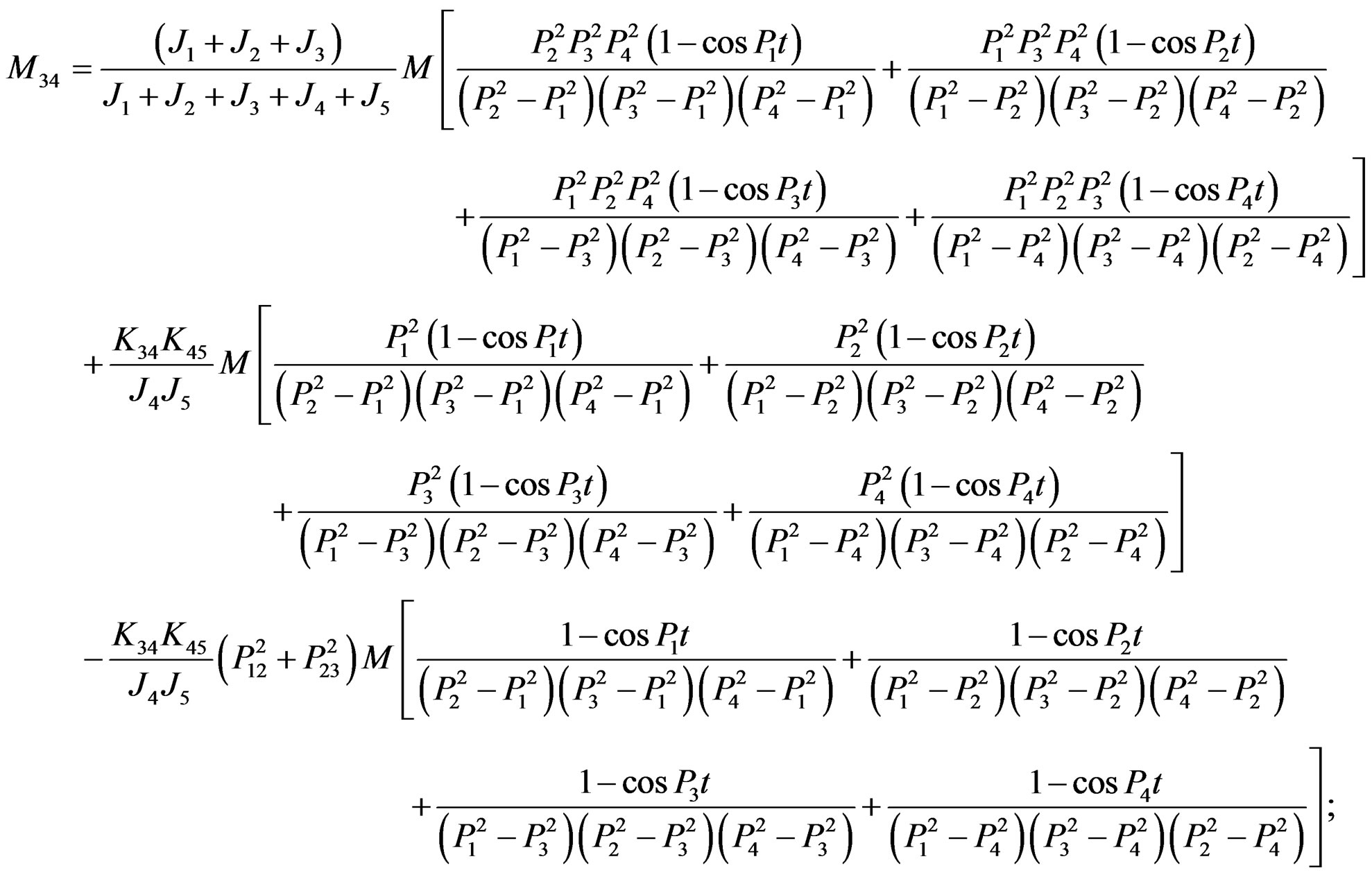
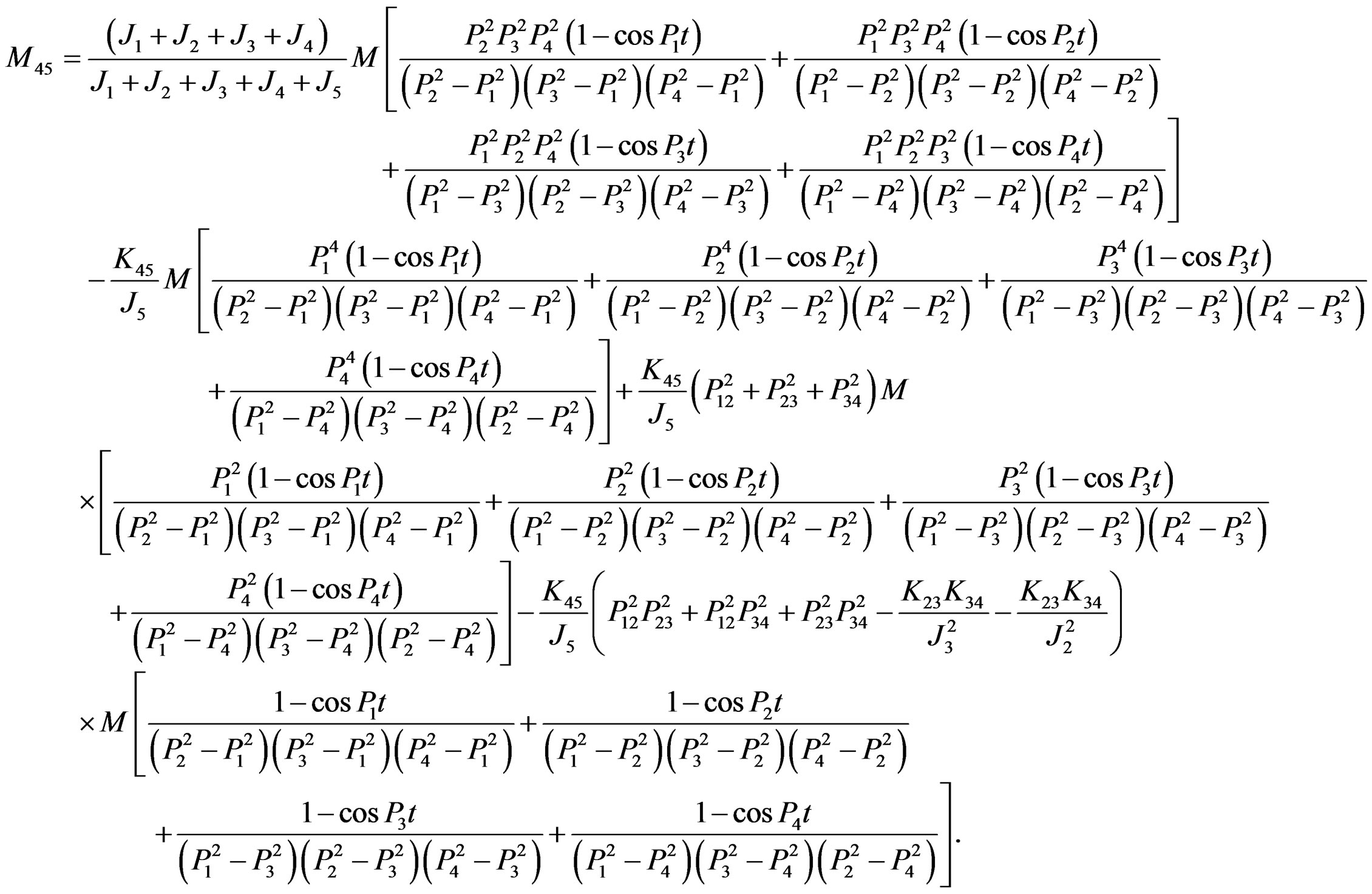
If we follow the differential operator  of numerator part in its faction has effect on input function in general mathematics handbook [4] and the teaching material of constant differential equations in textbook [1,2] (that is to say, we carry out derivative operation), thus we can acquire the following items if
of numerator part in its faction has effect on input function in general mathematics handbook [4] and the teaching material of constant differential equations in textbook [1,2] (that is to say, we carry out derivative operation), thus we can acquire the following items if  is a step function and initial conditions are zero:
is a step function and initial conditions are zero:
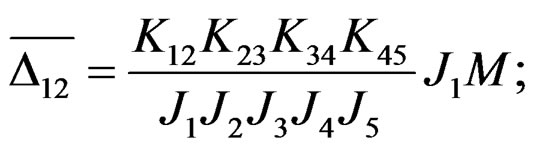
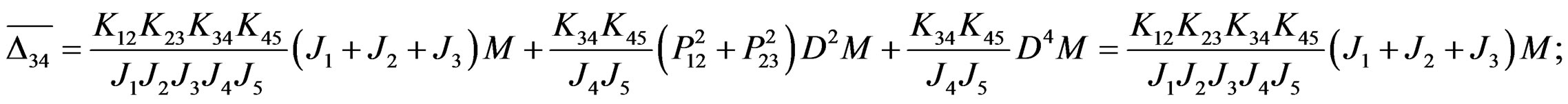
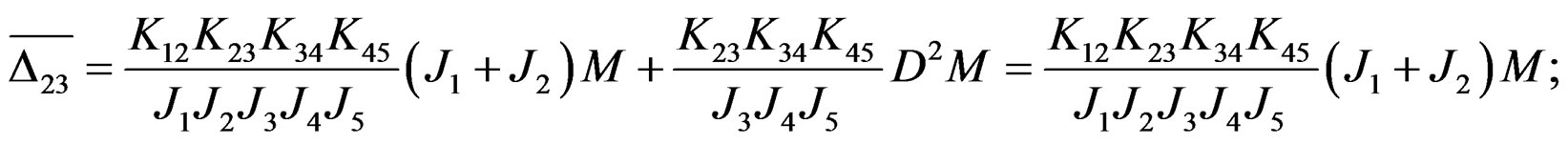
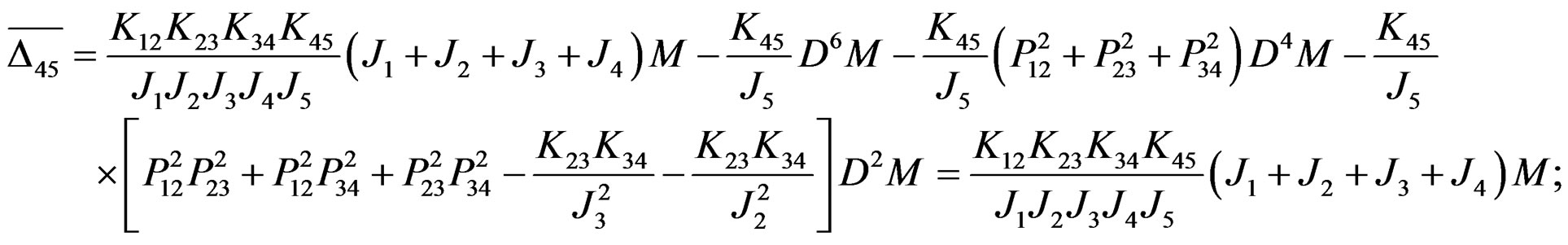
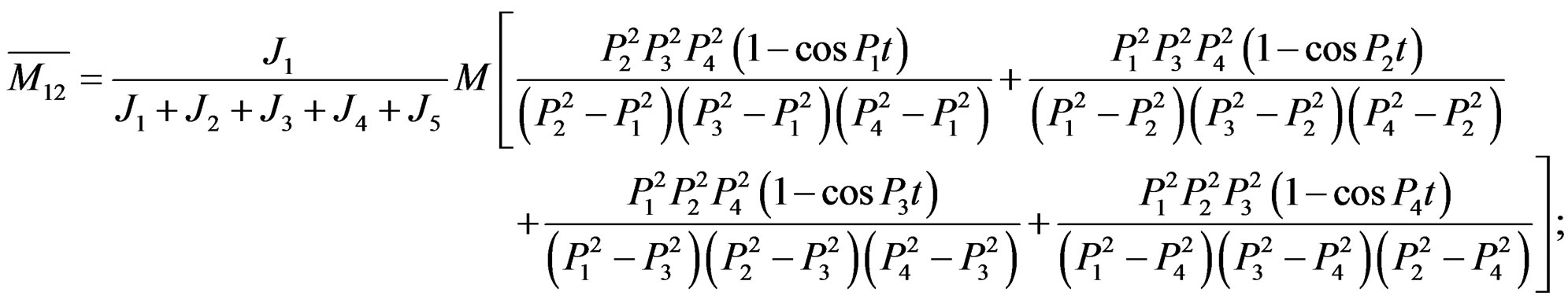

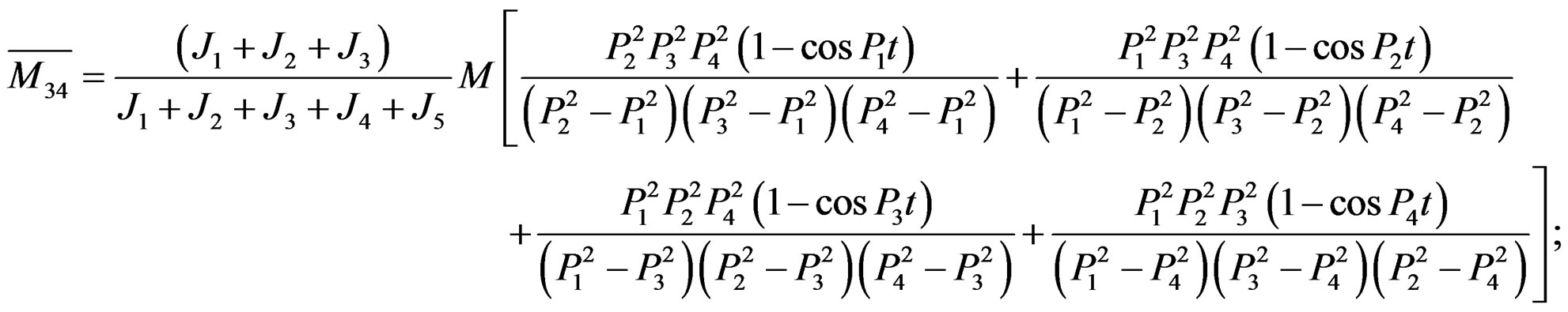
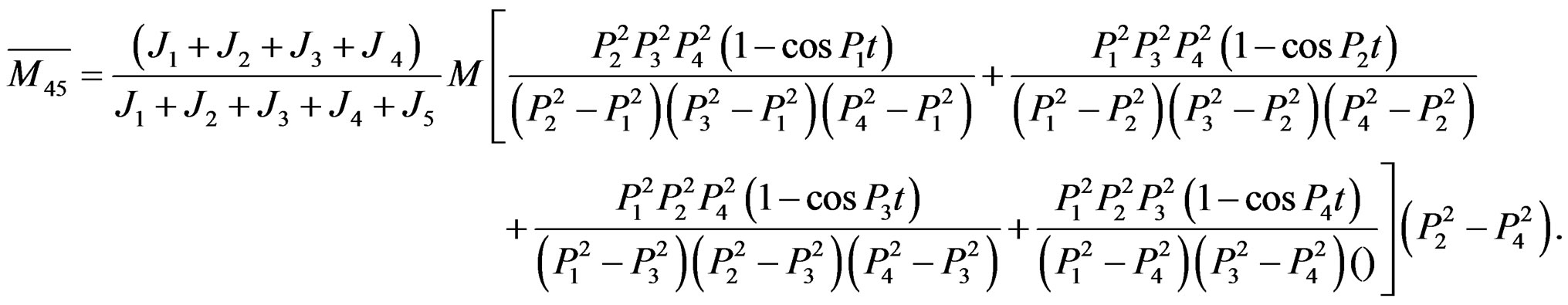
Obviously, the above result of torsional vibration dynamic resonance in every axial segment shows only related to the distribution coefficients of moment of inertia with the same coefficients of frequency difference and the same time of every axial segment attained by peak moment, but it is inappropriate in practice. Above result seems only like the ordinary dynamic questions (the starting of acceleration movement and the braking decaleration movement); however, it apparently does not belong to questions of torsional vibration. Consequently, the results via the new differential operator method we mentioned above are not only as same as that by Laplace transform and model analysis method, but also coincide with that of recently widely used in modal matrix method in mechanical vibration.
Now we take main transmission system in 2300 medium plate rolling-mill in the original serious accident we referred as an example, although it is some roughly approximate to the rectal serial five masses system (generally speaking, it should be taken as a branch system, and here it is only for a practical application of above method).
We solve the quantities as follows by the related data:
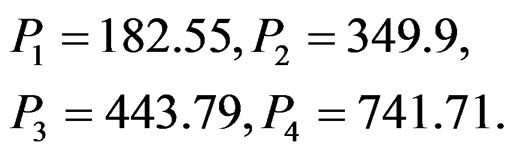
Then we have
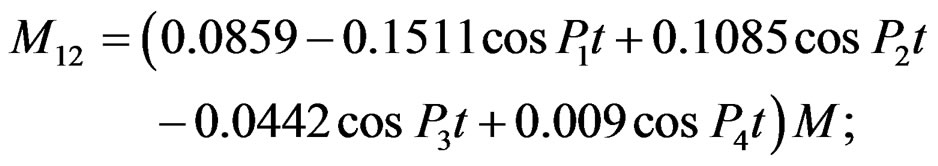
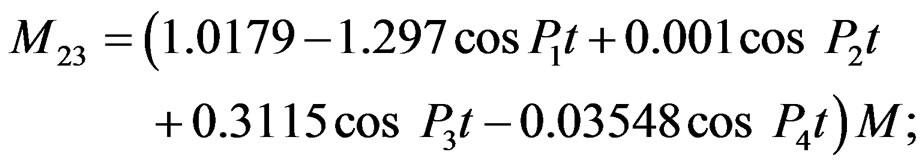
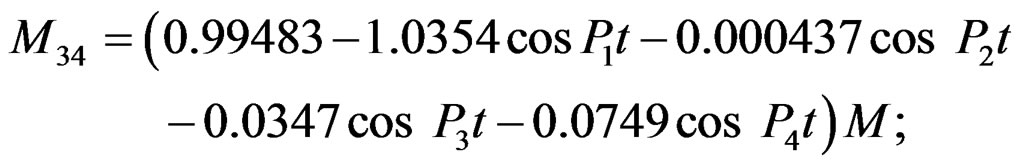
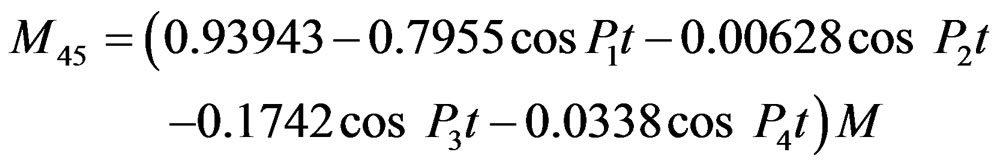
According to appearing time of the peak moment, we obtain the peak moment value in the Table 1 by the formula below:
Torque Amplification Factor (TAF) = peak moment value/Applied to excited vibration moment maximum value on roller.
3. Conclusions
From the above analysis we have the same solutions as that in Laplace transformation and modal analysis method, such that we solved the accident quickly. According to the torque amplification factor (TAF) in our analysis, the related unit in the factory revised and adjusted the size of the safety pin quickly, and thereafter such similar huge accident has never happened.
As a problem in dynamic resonance of torsional vibration, model analysis method belongs to numerical computing method, but it cannot analyze the effects on all parameters in practical applications. It is easy for us to utilize the new differential operator method to analyze the effect on each parameter compared with other methods. It has been widely extended and applied to all related fields in mechanics and engineering, which we clearly clarify the errors mentioned in the references [1-4] here. In addition, the new differential operator method has been successfully implemented to solve other governing equations in the problems in mechanical dynamics, see pp. 71-89 in Chapter 15 in [9], where [9] wins the second award of Scientific and Technical Prize in Chinese Mechanical Industry in 2010.
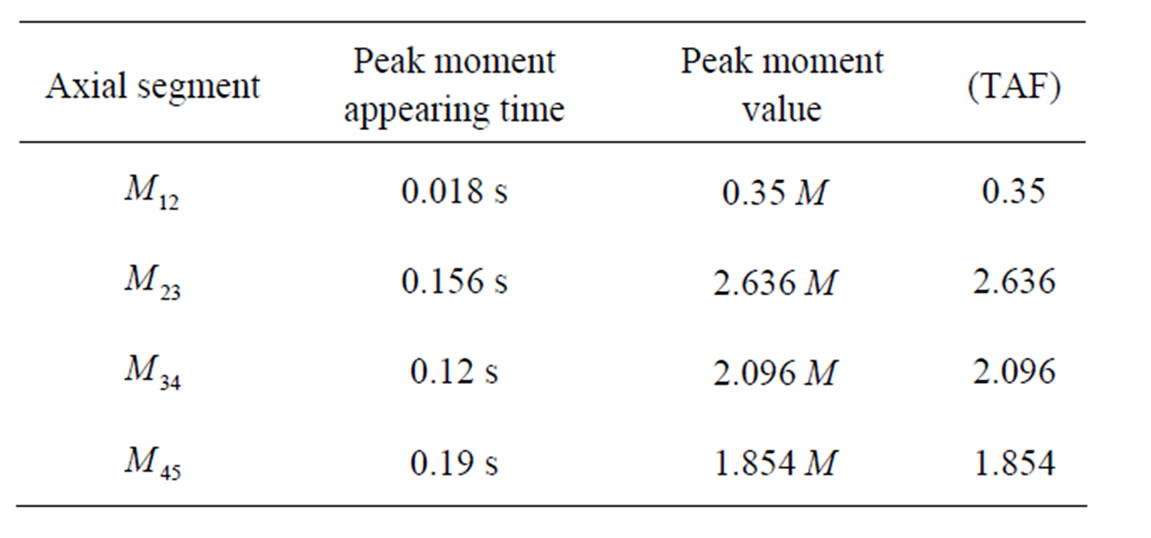
Table 1. Torsional vibration quantities in the example in this paper.
4. Acknowledgements
We very much appreciate that Professors of Xianzhi Liu in Shandong University and Weichang Qian in Shanghai University who have supported this paper greatly.
REFERENCES
- Department of Mathematics, Shanghai Tongji University, “Advanced Mathematics I,” 6th Edition (in Chinese), Publishing House of High Education, Beijing, 2007, pp. 350-352.
- C. H. Edwards and D. E. Penney, “Elementary Differential Equations,” 6th Edition, Pearson Prentice Hall, Upper Saddle River, 2008, pp. 340-345.
- S. E. Kerufunikefu, “Mechanical Dynamics with Elastic Key Ring,” (in Russian, No Further Version), Kiev, 1961, pp. 86-89.
- “Mathematics Handbook,” (in Chinese), Publishing House of People Education, Beijing, 1979, pp. 675-677 (reprinted by Publishing House of High Education, Beijing, 1999).
- R. P. Agnew, “Differential Equations,” 2nd Edition, McGraw-Hill, Book Company, Inc., New York, Toronto, London, 1960, pp. 216-250.
- L. E. Ėl’sgolts, “Differential Equations,” in the Series International Monographs on Advanced Mathematics and Physics, Gordon and Breach Publishers, Inc., New York, and Hindustan Publishing Corporation, Delhi, 1961, pp. 145-155.
- C.-S. Ji, “A New Solution of Constant Differential Equation Group by Differential Operator and Application in Calculating Rolling-Mill Torsion Vibration,” Proceedings of the 6th International Modal Analysis Conference, Kissimmee, 1-4 February 1988, pp. 598-602.
- Z. Zheng, “Mechanical Vibration I,” (in Chinese), Publishing House of Mechanical Industry, Beijing, 1980.
- “Mechanical Design Handbook,” (in Chinese), Publishing House of Chemical Industry, Beijing, 2009.

