Open Journal of Biophysics
Vol.4 No.3(2014), Article
ID:48417,7
pages
DOI:10.4236/ojbiphy.2014.43011
Nonlinear Polarizability of Erythrocytes in Non-Uniform Alternating Electric Field
Konstantin V. Generalov1, Vladimir M. Generalov1, Alexander S. Safatov1, Alexander G. Durymanov1, Galins A. Buryak1, Margarita V. Kruchinina2, Mikhail I. Voevoda2, Andrey A. Gromov2
1Federal Budget Research Institution State Research Center of Virology and Biotechnology Vector, Koltsovo, Novosibirsk Region, Russian Federation
2Federal State Budgetary Institution of Internal and Preventive Medicine Siberian Branch under the Russian Academy of Medical Sciences, Novosibirsk, Russian Federation
Email: general@vector.nsc.ru
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 26 May 2014; revised 25 June 2014; accepted 24 July 2014
ABSTRACT
Nonlinear polarizability of erythrocytes in non-uniform alternating electric field (NUAEF) was proved theoretically and experimentally by dielectrophoresis method. The paper presents experimental evidence of the nonlinear polarizability of erythrocytes in the non-uniform alternating electric field. The rotation of erythrocyte around its own axis at more than one revolution per second in the non-uniform alternating electric field in the frequency range 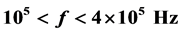 and the electric field intensity
and the electric field intensity 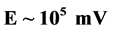 is the evidence of its nonlinear polarizability. The theoretical analysis of the density of electric charges capable of overcoming the membrane potential was carried out on the basis of statistical mechanics, the thermal equilibrium in which the particle stays. The nonlinear polarizability of the erythrocyte emerges if the voltage on the membrane exceeds
is the evidence of its nonlinear polarizability. The theoretical analysis of the density of electric charges capable of overcoming the membrane potential was carried out on the basis of statistical mechanics, the thermal equilibrium in which the particle stays. The nonlinear polarizability of the erythrocyte emerges if the voltage on the membrane exceeds , which was theoretically proved. The alternating electric field from the donor erythrocyte with the amplitude exceeding
, which was theoretically proved. The alternating electric field from the donor erythrocyte with the amplitude exceeding  forms the constant component of the current
forms the constant component of the current 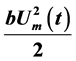 in the cytoplasm of the recipient erythrocyte whose energy can be considered as a signal one. The nonlinear equivalent electric circuit of the cell was proposed.
in the cytoplasm of the recipient erythrocyte whose energy can be considered as a signal one. The nonlinear equivalent electric circuit of the cell was proposed.
Keywords:Dielectrophoresis, Polarizability, Rotation, Erythrocyte, Nonlinearity

1. Introduction
The study of polarization and deformation of erythrocytes is an urgent problem in the diagnosis of some diseases. The above characteristics are interrelated in their reaction to practically any pathological process in the organism [1] -[4] . The polarization of a cell in an external electric field is accompanied by the displacement of its electric charges relative to the equilibrium position, the formation of an induced dipole moment and, as a result, the overall deformation of the total cell volume [1] [5] . In turn, the deformability of erythrocytes also depends on their viscoelastic properties i.e. total rigidity and viscosity [6] . The deformation of an erythrocyte is obviously limited by its own finite mass, and the displacement of electric charges relative to the equilibrium position is limited by their electrostatic repulsion in the cell closed volume. Thus, these limitations create conditions for the nonlinear polarization of erythrocytes in an external electric field.
The aim of the work was to study the nonlinear polarizability of erythrocytes in NUAEF with an intensity ~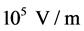 and a frequency range of
and a frequency range of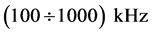 .
.
2. Materials and Methods
Human erythrocytes obtained from whole blood drawn from the donor’s vein were used in the study. To conduct the dielectrophoresis analysis, 2 ml of blood were collected with vacutainers in 3.7% citrate buffer at a ratio of 9:1. Immediately before the experiment, 10 μl of blood were diluted in  sucrose solution 30-fold. Specific resistance of
sucrose solution 30-fold. Specific resistance of 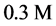 sucrose solution was
sucrose solution was  ohm∙m, pH
ohm∙m, pH . The cells were suspended in
. The cells were suspended in 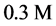 sucrose solution to a concentration of 107 cm−3. Blood collection from donors was performed with the approval of the Biomedical Ethics Committee of the Federal Budget Research Institution Research Institute of Therapy, Siberian Branch of Russian Academy of Medical Sciences (Protocol # 36 of the meeting of September 18, 2012).
sucrose solution to a concentration of 107 cm−3. Blood collection from donors was performed with the approval of the Biomedical Ethics Committee of the Federal Budget Research Institution Research Institute of Therapy, Siberian Branch of Russian Academy of Medical Sciences (Protocol # 36 of the meeting of September 18, 2012).
Experiments were performed in a measuring cell where NUAEF was created. Detailed description of the measuring cell and the laboratory device as a whole is presented in [6] . Measurements were carried out in the frequency range . The harmonic voltage
. The harmonic voltage  was applied to the electrodes through the capacitor. As a result, the harmonic voltage on the electrodes was lacking the constant component.
was applied to the electrodes through the capacitor. As a result, the harmonic voltage on the electrodes was lacking the constant component.
Video monitoring and recording of the speed of erythrocyte rotation around its own axis were carried by the position of a typical natural reference point on its surface. The cell turnover period was measured using an electronic clock built into the computer.
3. Results and Discussion
3.1. Experimental Part
Experimental observations demonstrated a slow rotation of erythrocytes around their own axes with varying frequency in the frequency range of 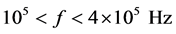 and the electric field intensity
and the electric field intensity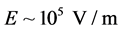 . Figure 1 shows the dynamics of rotation of a selected individual cell. Measurements showed that its rotation frequency was ~
. Figure 1 shows the dynamics of rotation of a selected individual cell. Measurements showed that its rotation frequency was ~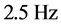 .
.

Figure 1. The dynamics of erythrocyte rotation around its own axis in non-uniform alternating electric field. The arrow shows the position of the natural reference point on the cell membrane monitored during the rotation process.
3.2. The Oretical Justification
The external electric field 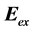 with the frequency
with the frequency ![]() and the phase
and the phase  applied to the cell induces the redistribution (polarization) of the set
applied to the cell induces the redistribution (polarization) of the set 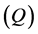 of its free and bound, positive
of its free and bound, positive 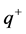 and negative
and negative 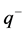 charges within the whole cell volume. As a result of polarization, in the cell there emerge uncompensated charges, which create within it its own field with the intensity
charges within the whole cell volume. As a result of polarization, in the cell there emerge uncompensated charges, which create within it its own field with the intensity ![]() directed against the external one,
directed against the external one,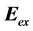 . The field in the cell volume forms the induced dipole
. The field in the cell volume forms the induced dipole![]() , which is the sum of a set of n elementary
, which is the sum of a set of n elementary 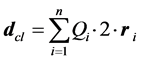 [5] [9] . In NUAEF, the cell dipole is influenced by the time-averaged force vector, which makes the cell move [10] .
[5] [9] . In NUAEF, the cell dipole is influenced by the time-averaged force vector, which makes the cell move [10] .
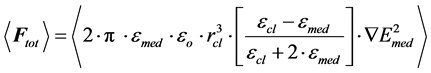 (1)
(1)
where: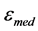 —dielectric permittivity of the medium;
—dielectric permittivity of the medium;
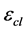 —dielectric permittivity of the cell;
—dielectric permittivity of the cell;
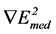 —the gradient of the square of intensity of the medium electric field;
—the gradient of the square of intensity of the medium electric field;
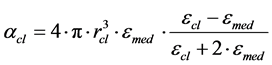 —polarizability coefficient of a spherical cell along a single selected direction, for example, axis
—polarizability coefficient of a spherical cell along a single selected direction, for example, axis .
.
The vector of the cell electric field intensity ![]() with the frequency
with the frequency 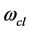 and the phase
and the phase ![]() follows the vector
follows the vector 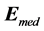
![]()
The superposition of two harmonic oscillations  results in the emergence of the frequency combinations
results in the emergence of the frequency combinations .
.
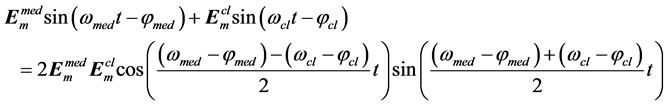 (2)
(2)
The condition 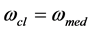 and
and 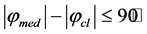 is fulfilled for the linear polarization of a cell. If the frequencies
is fulfilled for the linear polarization of a cell. If the frequencies 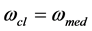 are equal to each other up to the phase
are equal to each other up to the phase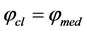 , any rotation around own axis is impossible (2).
, any rotation around own axis is impossible (2).
The nonlinear polarization of a cell requires the condition 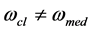 to be fulfilled. If
to be fulfilled. If , the cell starts rotating around its own axis, which can be recorded and analyzed by instrumental video monitoring.
, the cell starts rotating around its own axis, which can be recorded and analyzed by instrumental video monitoring.
The typical value of the erythrocyte transmembrane potential is about  [11] . This potential creates on the membrane a potential barrier with the electric field intensity ~
[11] . This potential creates on the membrane a potential barrier with the electric field intensity ~ whose vector is normal to the cell surface. According to the statistical mechanics, the charge1 (ion) should possess the energy required for overcoming the total potential barrier of the cell membrane
whose vector is normal to the cell surface. According to the statistical mechanics, the charge1 (ion) should possess the energy required for overcoming the total potential barrier of the cell membrane 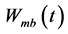
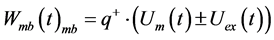 (3)
(3)
where:
 —the unit positive charge of the ion
—the unit positive charge of the ion  [K];
[K];
 —the membrane own instantaneous voltage [B];
—the membrane own instantaneous voltage [B];
 —the external medium voltage affecting the membrane
—the external medium voltage affecting the membrane 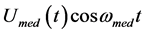 [В].
[В].
The density of positive charges capable of overcoming the above barrier is described by Expression [5] .
 (4)
(4)
where:
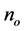 —the initial density of positive charges on the membrane surface depending the concentration and thermal equilibrium of ions in cell suspension [5] ;
—the initial density of positive charges on the membrane surface depending the concentration and thermal equilibrium of ions in cell suspension [5] ;
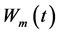 —the initial potential energy of the membrane;
—the initial potential energy of the membrane;
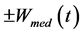 —the potential energy of the external medium affecting the membrane [J];
—the potential energy of the external medium affecting the membrane [J];
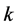 —Boltzman constant [J/deg];
—Boltzman constant [J/deg];
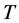 is the absolute temperature [K].
is the absolute temperature [K].
The exponential function (4) can be determined using the Maclaurin series, which converges at any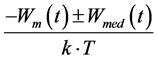 [7] .
[7] .
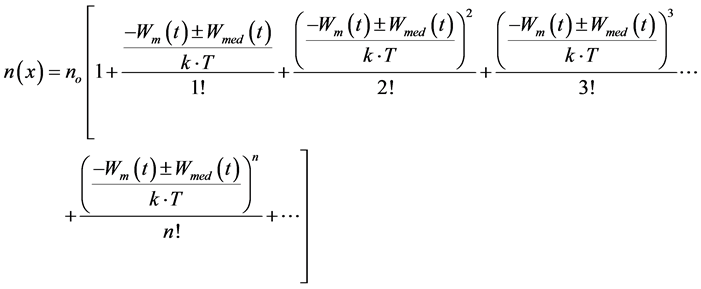 (5)
(5)
If the summand  is much smaller than 1,the contributions of sum-mands of higher orders (starting from the third, quadratic, one) in (5) can be neglected. As a result, the density of the charges capable of overcoming the potential barrier has a linear character. If the exponent
is much smaller than 1,the contributions of sum-mands of higher orders (starting from the third, quadratic, one) in (5) can be neglected. As a result, the density of the charges capable of overcoming the potential barrier has a linear character. If the exponent 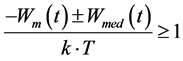 is equal to or more than 1, the contributions of individual summands of higher orders to nonlinearity become dominant. However, with increasing n value in (5) a general trend is observed: the values of individual summands of the series rapidly decrease.
is equal to or more than 1, the contributions of individual summands of higher orders to nonlinearity become dominant. However, with increasing n value in (5) a general trend is observed: the values of individual summands of the series rapidly decrease.
The interrelations between Expressions (1, 3, 4, 5) allow us to consider the cell polarization process to be nonlinear, too. From the mathematical point of view, nonlinearity in Equation (5) emerges when 
and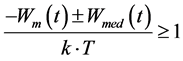 . Retaining the summand
. Retaining the summand 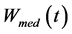 and proceeding from the classical definition that current
and proceeding from the classical definition that current 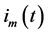 is determined by the rate of change of the charge
is determined by the rate of change of the charge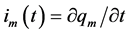 , Equation (5) can be rewritten in a form of a sum of currents flowing through the membrane at
, Equation (5) can be rewritten in a form of a sum of currents flowing through the membrane at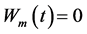 .
.
 (6)
(6)
From Equation (6), the calculated values 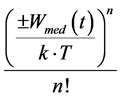 of the members of the Maclaurin series depending on their serial numbers
of the members of the Maclaurin series depending on their serial numbers 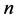 are presented in Figure 2, Figure 3. By further simplifying Equation (6), let us reduce it to.
are presented in Figure 2, Figure 3. By further simplifying Equation (6), let us reduce it to.
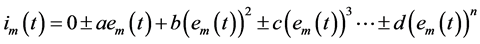 (7)
(7)
where:
![]() —the change in the constant component of the membrane current, equals zero
—the change in the constant component of the membrane current, equals zero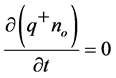 ;
;
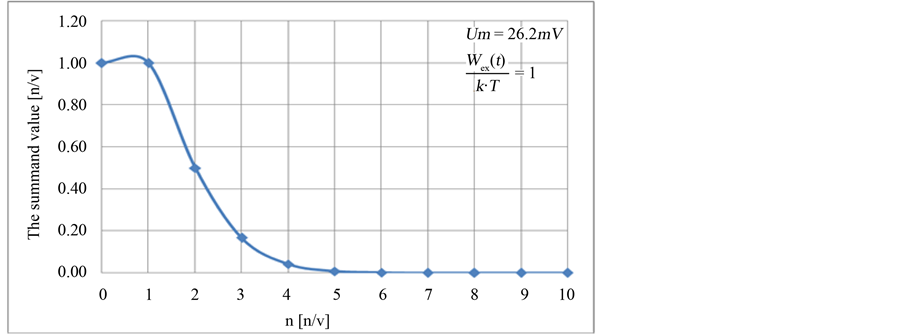
Figure 2. The calculated values  of the summands of the Maclaurin series determining the current through the cell membrane depending on
of the summands of the Maclaurin series determining the current through the cell membrane depending on 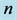 and
and![]() , the voltage across the membrane.
, the voltage across the membrane.

Figure 3. The calculated values 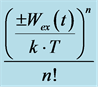 of the summands of the Maclaurin series determining the current through the cell membrane depending on
of the summands of the Maclaurin series determining the current through the cell membrane depending on 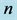 and
and![]() , the voltage across the membrane.
, the voltage across the membrane.
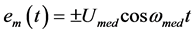 is the instantaneous voltage of the membrane;
is the instantaneous voltage of the membrane;
![]() are the coefficients of proportionality, in particular,
are the coefficients of proportionality, in particular,  is resistance with the dimension [ohm].
is resistance with the dimension [ohm].
From the consideration of the first three summands of Equation (7) it follows that the alternating current of the membrane contains only the linear and the quadratic components
![]()
Taking into account that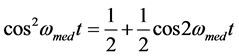 , let us write
, let us write
 (8)
(8)
The analysis of Expression (8) shows that the total current through the cell membrane is determined by the combination of individual harmonic components with frequencies 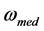 and
and 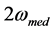 and the constant component
and the constant component . This allows us to consider the cell as a nonlinear element, which explains the emergence of the cell currents with the frequency
. This allows us to consider the cell as a nonlinear element, which explains the emergence of the cell currents with the frequency 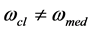 and that of beat frequencies
and that of beat frequencies 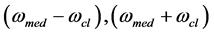 determining the cell rotation around its own axis.
determining the cell rotation around its own axis.
The linear model of polarization of the medium and the cell in the external alternating electric field is relatively simple. In each point, the electric field induces in their volume the dipoles with the harmonic frequency![]() , which coincides with the external one. In the case of the nonlinear polarization, the formation of the induced dipole moment of the cell by electric charges is associated with the fact that their movement is not harmonic any more. In this case, the energy of the cyclic frequency
, which coincides with the external one. In the case of the nonlinear polarization, the formation of the induced dipole moment of the cell by electric charges is associated with the fact that their movement is not harmonic any more. In this case, the energy of the cyclic frequency ![]() of the external field is transferred to the second and higher harmonics, and there also emerge multiple combinations between them [11] .
of the external field is transferred to the second and higher harmonics, and there also emerge multiple combinations between them [11] .
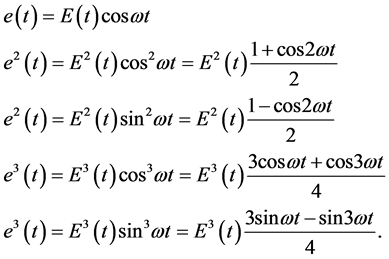
The analysis of the presented known trigonometric expressions also shows that the member of the series with the serial number 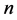 in (6) also takes into account the harmonics
in (6) also takes into account the harmonics 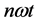 of the current flowing through the cell membrane. Thus, in Figure 2, Figure 3, the serial number
of the current flowing through the cell membrane. Thus, in Figure 2, Figure 3, the serial number 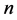 along the abscissa agrees with the current harmonics.
along the abscissa agrees with the current harmonics.
Experimental data and the conducted theoretical analysis of the interaction between the cell and alternating electric field suggest that under the study conditions the erythrocyte can be presented as a nonlinear element whose membrane permeability for positive ions is higher in one direction than in the reverse direction. This is consistent with the selective permeability of the membrane, for example, for potassium ions ![]() [12] known from literature. Interestingly, the
[12] known from literature. Interestingly, the 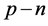 transition in electronic devices, for example, a diode is characterized by similar different conductivities in different directions [13] . The special case of the nonlinear equivalent electric circuit of the cell for positive charges is shown in Figure 4 where the membrane is presented by a diode with nonlinear resistance and capacity
transition in electronic devices, for example, a diode is characterized by similar different conductivities in different directions [13] . The special case of the nonlinear equivalent electric circuit of the cell for positive charges is shown in Figure 4 where the membrane is presented by a diode with nonlinear resistance and capacity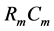 .
.
The conducted work allowed us to draw the following conclusions.

Figure 4. The nonlinear equivalent electric circuit of the cell for positive charges.![]() ,
, ![]() and
and ![]() are the capacities of the membrane, cytoplasm and medium (cell suspension);
are the capacities of the membrane, cytoplasm and medium (cell suspension); , are the resistances of the membrane, cytoplasm and medium.
, are the resistances of the membrane, cytoplasm and medium.
4. Conclusions
1) The nonlinear polarizability of human erythrocytes is observed in non-uniform alternating electric field with the intensity  in the frequency range of
in the frequency range of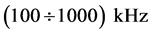 .
.
2) The nonlinear polarizability of erythrocytes in non-uniform alternating electric field causes their rotation around their own axes with the frequency exceeding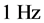 .
.
3) The external harmonic electric field affecting the cell is created in the cell cytoplasm in the form of a nonlinear uniform2 field with a constant component and a broad frequency range due to the electric properties of the cell membrane.
4) The alternating electric field from the donor erythrocyte with the amplitude exceeding  forms the constant component of the current
forms the constant component of the current  in the cytoplasm of the recipient erythrocyte whose energy can be considered as a signal one.
in the cytoplasm of the recipient erythrocyte whose energy can be considered as a signal one.
References
- Zinchuk, V.V. (2001) Erythrocyte Deformability: Physiological Aspects of Progress in Physiological Sciences. Advances in Physiological Sciences, 32, 66-78 (in Russian).
- Torkhovskaya, T.I., Artemona, L.G., Khodzhakuliev, B.G., Rudenko, T.S., Polessky, V.A. and Azizova, O.A. (1980) Structural and Functional Changes in Erythrocyte Membranes at Experimental Atherosclerosis. Bulletin of Experimental Biology and Medicine, 89, 675-678 (in Russian). http://dx.doi.org/10.1007/BF00836241
- Kruchinina, M.V., Kurilovich, S.A., Parulikova, M.V., Bakirov, T.S., Generalov, V.M., Pak, A.V. and Zvolskiy, I.L. (2005) Electric and Viscoelastic Properties of Erythrocytes of Patients with Diffuse Pathology of the Liver. Proceeding of the Academy of Sciences, 401, 701-704 (in Russian).
- Kurilovich, S.A., Kruchinina, M.V., Gromov, A.A., Generalov, V.M., Bakirov, T.S., Rikhter, V.A. and Semenov, D.V. (2010) Justification of the Use of Essential Phospholipids at Chronic Liver Diseases: The Dynamics of Electric and Viscoelastic Parameters of Erythrocytes. Experimental and Clinical Gastroenterology, 11, 46-52 (in Russian).
- Feinman, R., Leitos, R., Sands, M. (1977) The Feinman Lectures on Physics. Electricity and Magnetism. Mir., Moscow (in Russian).
- Bakirov, T.S., Generalov, V.M. and Toporkov, V.S. (1998) The Measurement of Viscoelastic Properties of a Cell Using the Non-Uniform Alternating Electric Field. Biotechnology, 5, 88-96 (in Russian).
- Vorobiev, N.N. (1979) The Theory of Series. Nauka, Moscow, 408 (in Russian).
- Generalov, V.M., Bakirov, T.S., Pak, A.V., Zvolskiy, I.L., Zaitsev, B.N., Durymanov, A.G., Kruchinina, M.V., Kurilovich, S.A. and Sergeev, A.N. (2008) The Automated Device for Measurement of Viscoelastic Properties of Erythrocytes. High Technologies, 9, 28-33 (in Russian).
- Landau, L.D., Lifshits, E.M. Theoretical Physics (1982) Electrodymanics of Continuous Media. 8, 2th Edition, Nauka, Moscow (in Russian).
- Hughes, M.P. (2003) Nanoelectromechanics in Engineering and Biology. CRC PRESS, Boca Raton.
- Gelfand, I.M., Lvovsky, S.M., Toom, A.L. Trigonometry. (2002) Moscow, MCCME (in Russia)
- Iost, Kh. (1975) Cell Physiology. Mir., Moscow (in Russian).
- Lebedev, A.I. (2008) Physics of Semiconductor Devices. Physmathlit, Moscow (in Russian).
NOTES

1We will consider only positive charges, which move against the forces of electric field formed by the transmembrane potential.

2Landau L.D., Lifshits E.M. Theoretical Physics. V. 8. Electrodynamics of continuous media. 2nd edition, revised and expanded. Moscow: Nauka. 1982. 620 p.

