Open Journal of Metal
Vol.2 No.1(2012), Article ID:18314,10 pages DOI:10.4236/ojmetal.2012.21002
Consideration of Castability and Formability for New Magnesium Alloys
State Key Laboratory for Corrosion and Protections, Institute of Metal Research, Chinese Academy of Sciences, Shenyang, China
Email: *rschen@imr.ac.cn
Received January 11, 2012; revised February 10, 2012; accepted February 21, 2012
Keywords: Rolling Magnesium Alloy Sheets; Texture; Solidification Processing; Castabiltiy; Hot Tearing; Semisolid Forming
ABSTRACT
A comprehensive consideration based on castability or plastic formability, as well as mechanical properties for development of either cast magnesium alloys or wrought magnesium alloys is a very important issue. To develop new magnesium alloy sheets with high formability at room temperature, the microstructure, texture, ductility and anisotropy of rolled Mg-Zn-Gd alloy sheets were investigated. The sheets exhibit an excellent ultimate elongation of nearly 50% and an uniform elongation greater than 30% with a very low planar anisotropy. The new sheet has a random basal texture and the basal pole is tilted by maximum 40˚ from the normal direction towards the transverse direction. The majority of grains in the tilted texture have an orientation favorable for both basal slip and tensile twining because of their high Schmid factor. The low planar anisotropy, the large uniform elongations and the high strain hardening rate observed in the Mg-Zn-Gd sheets result in excellent room temperature formability, the Erichsen values reach ~8, well comparable with the conventional aluminum alloys sheets at room temperature. The solidification pathways and phase equilibria of Mg-Al-Ca alloys have been profoundly investigated by using thermal analysis and thermodynamic calculations. The relationship between hot tearing tendency and alloy compositions were discussed in terms of strength of the mushy zone, solidification pathways and feeding mechanisms, et al. Thixoforming refers to as that metal components are formed in their semi-solid state. Criteria for thixoforming are summarized and then the thixoformability of Mg-Al-Ca based alloys (AC alloys) are evaluated using the thermodynamic calculations based on the consideration of metallurgical parameters.
1. Introduction
Improving fuel efficiency and reducing emissions of vehicles can be achieved through lightweight construction. Magnesium and its alloys, as the lightest structural metals, offer a remarkable potential in this regard. However, their wide use is still restricted by their limited formability and castability.
The commercial magnesium sheets usually have poor ductility and strong anisotropy at room temperature [1], which limit their further forming and industrial applications. For example, the currently available AZ31 alloy sheets often exhibit low press and drawing formability at near room temperature, which have been attributed to a pronounced basal texture [2,3]. To improve the formability, it is desirable to develop magnesium sheets with weak basal texture and low anisotropy as well as excellent ductility at room temperature. The most notable way of modifying the texture of wrought magnesium products is by the addition of certain alloying Rare Earth (RE) elements [4,5]. Some papers have already reported the excellent room temperature formability of Mg-Zn alloys with dilute RE elements such as Ce, Y and Gd [6-9], and the authors have suggested that the dilute addition of RE elements induce not only a reduction in the intensity of the basal plane texture, but also a spreading of basal poles in the transverse direction (TD) [6-9], which lead to the excellent room temperature formability. Thus it is feasible to develop new magnesium sheets with high formability at room temperature by addition of RE.
Mg-Al-Ca system alloys have been attracted many researchers’ attentions due to their advantages, such as low cost, low density, ignition proof improvement, and most importantly, their excellent creep resistance and superior mechanical properties at elevated temperature [10,11]. Many efforts have been focused on the creep rupture and mechanical behavior of Mg-Al-Ca alloy at elevated temperature [12,13]. However, these alloys are not free of problems either. For instance, it is reported that cast magnesium alloys containing Ca addition in excess of 1 wt% are known to be prone to hot tearing, sticking to dies and increasing microporosity level [10,14].
In the present research, we report the texture, ductility, strain-hardening behavior, and stretch formability of rolled Mg-Zn-Gd alloys sheets at room temperature. High roomtemperature ductility and easy formability in these alloy sheets will be presented. Then, a quite systematical investigation on the solidification pathway, castability and hot tearing susceptibility of Mg-Al-Ca alloys will be evaluated and discussed. In addition, the semi-solid formability of Mg-Al-Ca alloys at Mg-rich corner is predicted by thermodynamic calculation, which will provide some guide for future alloy composition design for semisolid forming.
2. Experimental Procedures
The alloy denoted as ZG11, ZG21, GZ21, and GZ31 were examined in the present study. The chemical compositions were Mg-1.20Zn-0.79Gd, Mg-2.26Zn-0.74Gd, Mg- 1.68Gd-1.11Zn, and Mg-2.74Gd-1.06Zn (wt%), respectively. They were prepared with pure Mg (99.9%), Zn (99.9%) and Gd (99.5%) by melting under the protection of a mixed SF6 (1 vol%) and CO2 (99 vol%) atmosphere. Ingots with a dimension of 75 mm × 200 mm × 200 mm were prepared by pouring the melt into a preheated steel mold. They were homogenized at 500˚C for 10 h, then quenched in water, and subsequently machined to slabs with a dimension of 200 mm × 70 mm × 20 mm. The slabs were rolled to sheets at 430˚C with a final thickness of 3 mm. The rolling process started with an initial reduction of ~10% and the final reduction was ~30% resulting in a total reduction of 85%. After each pass, the rolling specimens were reheated to 430˚C and held for 20 min to maintain a consistent rolling temperature. The rolled sheets were annealed at 400˚C for 1 h after the last rolling pass. For comparison, AZ31 (Mg-3Al-1Zn-0.2Mn, by wt%) was selected as the counterpart since it was a popular magnesium alloy for rolled sheets products. The cast ingot of the AZ31 magnesium alloy was machined to a slab with a thickness of 20 mm, and was also processed identically to the rolled Mg-Gd-Zn alloys. Hereafter, RD, TD and ND denote the rolling, transverse and normal directions of the sheets, respectively.
For microstructure observations, samples were cut from the rolled sheets and etched in acetic picric (25 ml ethanol + 2 g picric acid + 5 ml acetic acid + 5 ml water). The grain sizes (L) were determined by analyzing the optical micrographs with a line-intercept method (d = 1.74 L). The phases were analyzed with a scanning electron microscope (SEM, Philips XL30 ESEM-FEG/EDAX) equipped with an energy-dispersive X-ray (EDX) spectroscopy analysis system. Texture analysis of the rolled samples in RD-TD plane was performed using the Schultz reflection method by X-ray diffraction. Calculated pole figures were obtained with the DIFFRACplus TEXEVAl software, using the measured incomplete {0002}, {10−10} and {10−11} pole figures.
The tensile tests were carried out at the angles of 0˚ (RD), 45˚ and 90˚ (TD) between the tensile direction and the RD at room temperature with an initial strain rate of 1 × 10−3 s−1. The true plastic strains along the plate width (εw), thickness (εt) and length directions (εl), respectively, were measured on the specimens deformed at a plastic strain of 8%. From these results the Lankford values (r-value) were calculated using the equation r = εw/εt = −εw/(εl + εw).
Circular blanks with a diameter of 60 mm and a thickness of 1 mm was machined from the specimens of rolled GZ21 and GZ31 sheets. Erichsen tests using a hemispherical punch with a diameter of 20 mm were carried out at room temperature to investigate the stretch formability of the specimens, and the Erichsen value (IE), which was the punch stroke at fracture initiation, was measured. The punch speed and blank-holder force were 5 mm/min and 10 kN, respectively. Graphite grease was used as a lubricant during the punch process.
Two series of alloys based on AZ91 alloy and AM50 alloys with different level of Ca addition (AZ91 with 1% and 2% Ca, named as AZX91x, and AM50 with 1%, 2% and 3% Ca, named as AMX50x alloys.) have been prepared in mild steel crucible with electrical resistance furnace. Samples for thermal analysis were cut from the same position of the cast ingots and machined into cylinders of 25 mm in diameter and 50 mm in length. The samples were remelted in a steel crucible in an electrical resistance furnace, then two shielded K-type thermocouples were immersed from the top of the crucible that was insulated from the top and the bottom. One thermocouple was placed at the center of the crucible (Tc) and the other close to the inner wall (Tw) at exactly the same depth in the melt (25 mm from the bottom). After holding 10 min at 720˚C, the crucible together with the two thermocouples were removed from the furnace and allowed cooling in air with a cooling rate of about 1 K/sec. The temperature changes were continuously recorded during the solidification process by using a high-speed data acquisition system linked to the computer. Samples for microstructural analysis were taken from the regions near the thermocouple tip after complete solidification. Observations of the microstructure were conducted on a Philips XL30 ESEM-FEG/EDAX scanning electron microscope (SEM). The compositions of the Ca-containing phases were analyzed by EDAX, and the reported values are the average of 10 measurements for each sample.
For AZX911 and AZX912 alloy, some as-cast ingots were hot extruded at 400˚C with a reduction ratio of 9:1. The extruded billets (15 mm diameter and 20 mm height) were then heated up to semisolid state (515˚C and 530˚C) for compression experiments in a hydraulic MTS machine. Specimens were isothermally held for 5 minutes before compression.
Thermodynamic calculations have been performed at the Mg-rich corner in the Mg-Al-Ca system using the Thermo-Calc software [15] by inputting thermodynamic data developed by Zhong Yu [16].
3. Results and Discussion
3.1. On the Rolled Mg-Zn-RE Alloy Sheets
3.1.1. Microstructure and Texture
The microstructures of the ZG11, ZG21, GZ21 and GZ31 rolled sheet, in the RD-TD plane are shown in Figure 1. All of them have equiaxed grain structures, with a few twins for GZ21 and GZ31 alloys. The average grain sizes are ~16 μm for ZG11 and GZ21, and ~12 μm for ZG21 and GZ31, respectively.
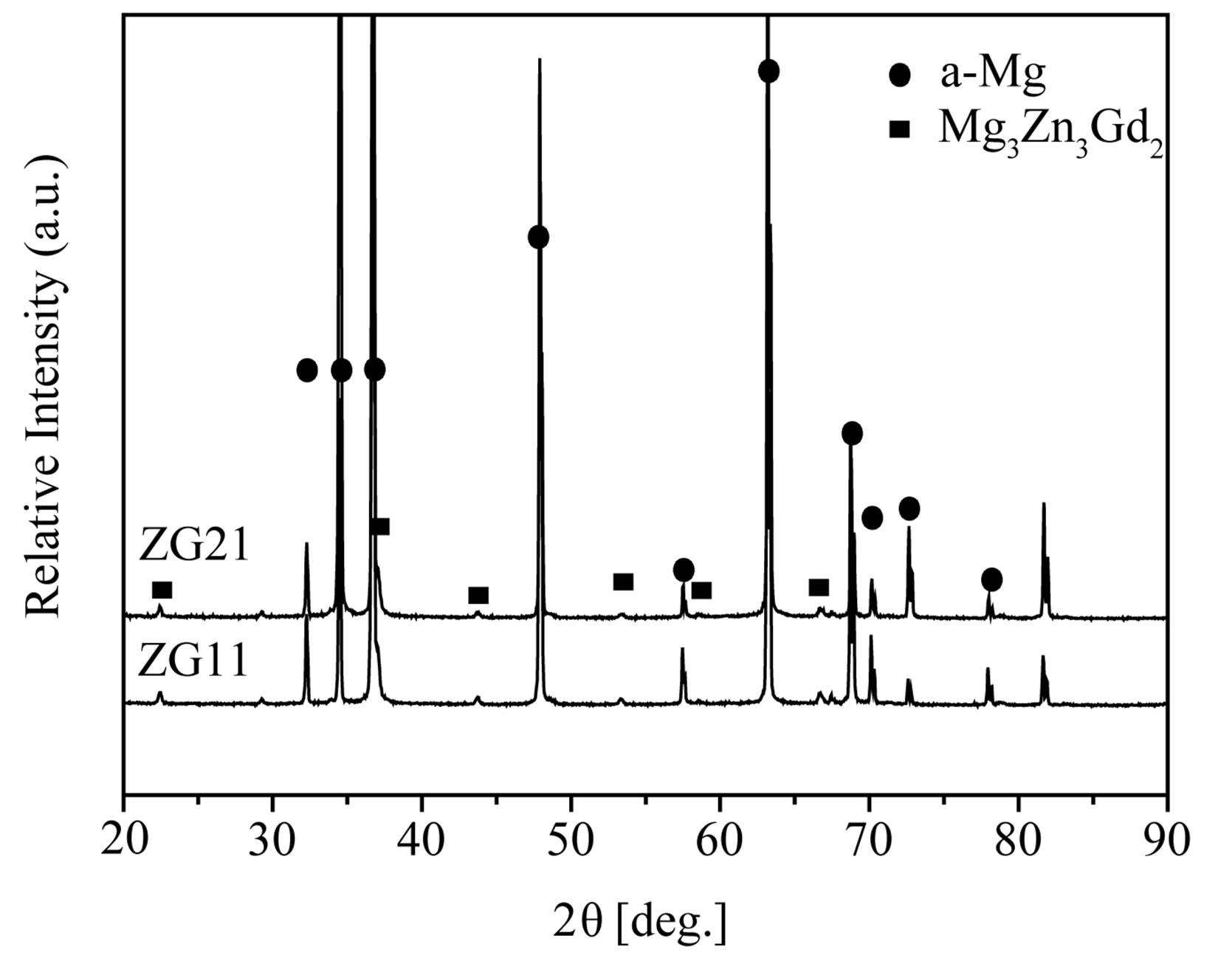
Figure 2 is the SEM images of the GZ31 sheet and corresponding EDX analysis results. In the high magnification of SEM images, there are many fine particles smaller than 2 μm and some larger particles ~10 μm (Figure 2(a)), which are homogeneously distributed in the matrix. A similar phase distribution is also observed in other Mg-Zn-Gd sheets. Studies by Yong Liu, et al. have shown that alloys with the Zn/Gd ratio (at.%) in the range of 0.25 - 1 consist of α-Mg, w-phase and an unknown phase [17], and the w-phase is a ternary MgZnGd compound with the fcc structure [18]. The phase constituents of the present four Mg-Zn-Gd alloys sheets by XRD analysis are shown in Figure 3. It is indicated that these hot-rolled alloys mainly consist of α-Mg solid solution, Mg3Gd2Zn3 (w-phase) and GdMg5 compounds. The larger particles are identified as GdMg5 according to results of the EDX analysis, as indicated by arrows A and B in Figure 2(a).
The (0002) plane pole figures of the rolled Mg-Zn-Gd and AZ31 alloys sheets are summarized in Figure 4 and reveal that the (0002) plane texture intensity of the MgZn-Gd alloys sheets are far lower than that of the rolled AZ31. The maximum intensity (~2) of the Mg-Zn-Gd sheets is only a quarter of that of AZ31 sheet, which indicates that the addition of Gd effectively weaken the basal texture intensity. The same trend has been observed in other Mg alloys containing RE elements [19-21]. Meanwhile, the pole figures of GZ21 and GZ31 alloys sheets show a non-basal texture with basal poles tilting about 30˚ from the normal direction towards RD and TD. And the peak intensity tilting towards TD is a little higher than that tilting to RD. The AZ31 sheet, on the other hand, shows a typical basal texture. In addition, the orientation distribution is wider in TD than in RD in the present Mg-Zn-Gd alloys sheets, while it is usually wider in RD in hot-rolled AZ31 sheet [22].
3.1.2. Room-Temperature Mechanical Properties and Formability
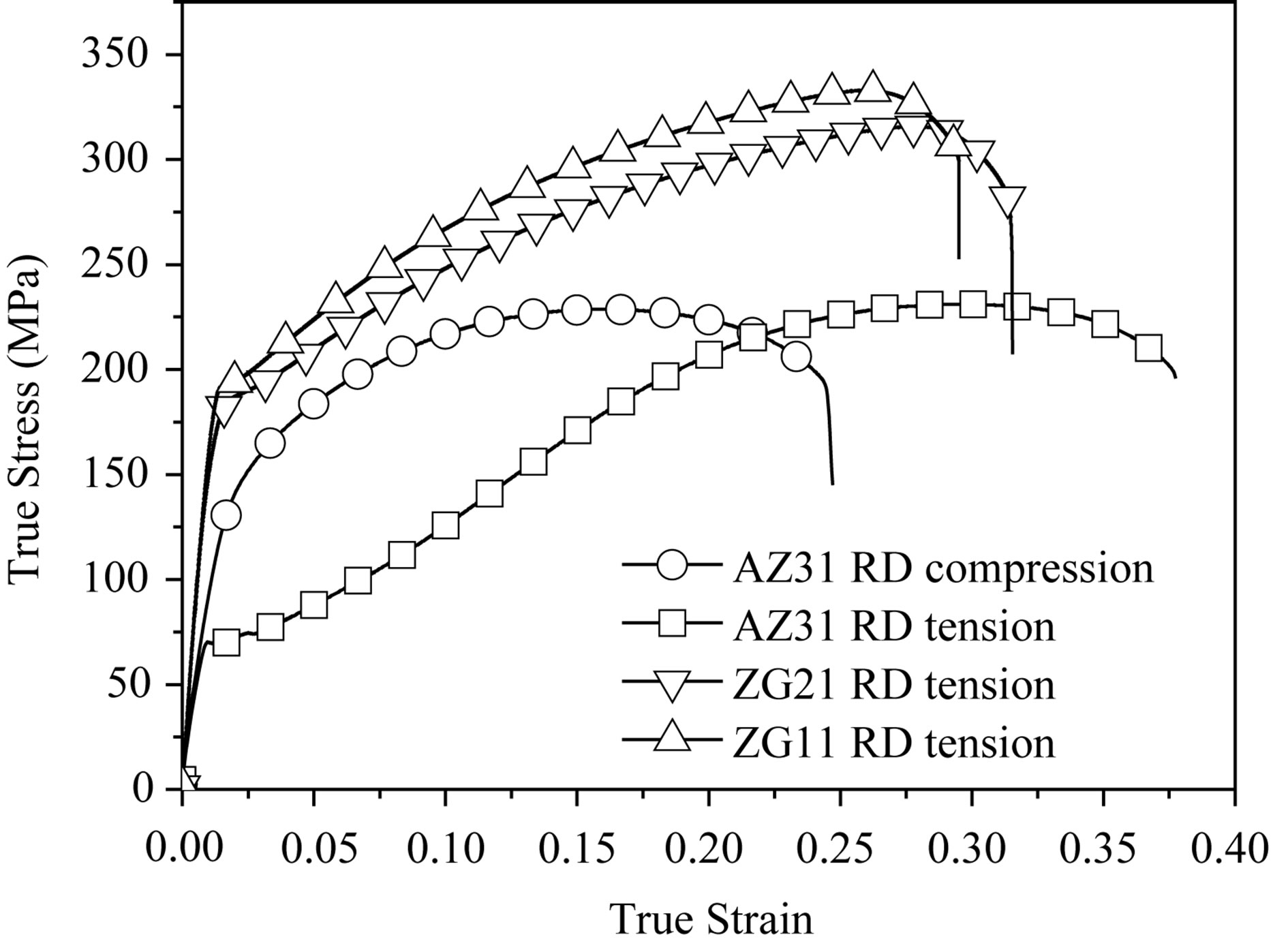
The tensile stress-strain curves of the Mg-Zn-Gd sheets are shown in Figure 5. To compare with those of the
 (a)
(a) (b)
(b) (c)
(c) (d)
(d)
Figure 1. Microstructures of the Mg-Zn-Gd rolled sheets (a) ZG11; (b) ZG21; (c) GZ21 and (d) GZ31.


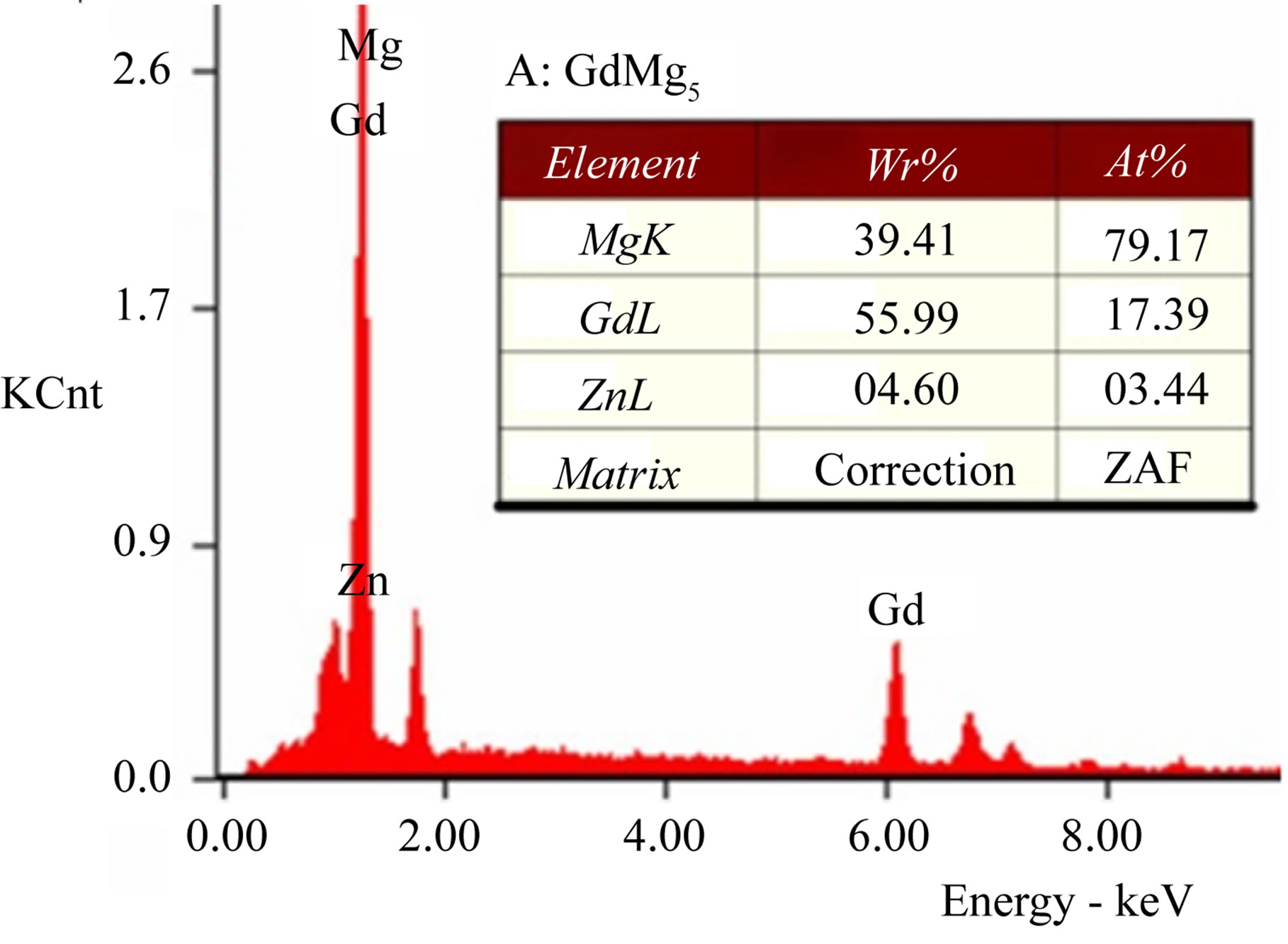
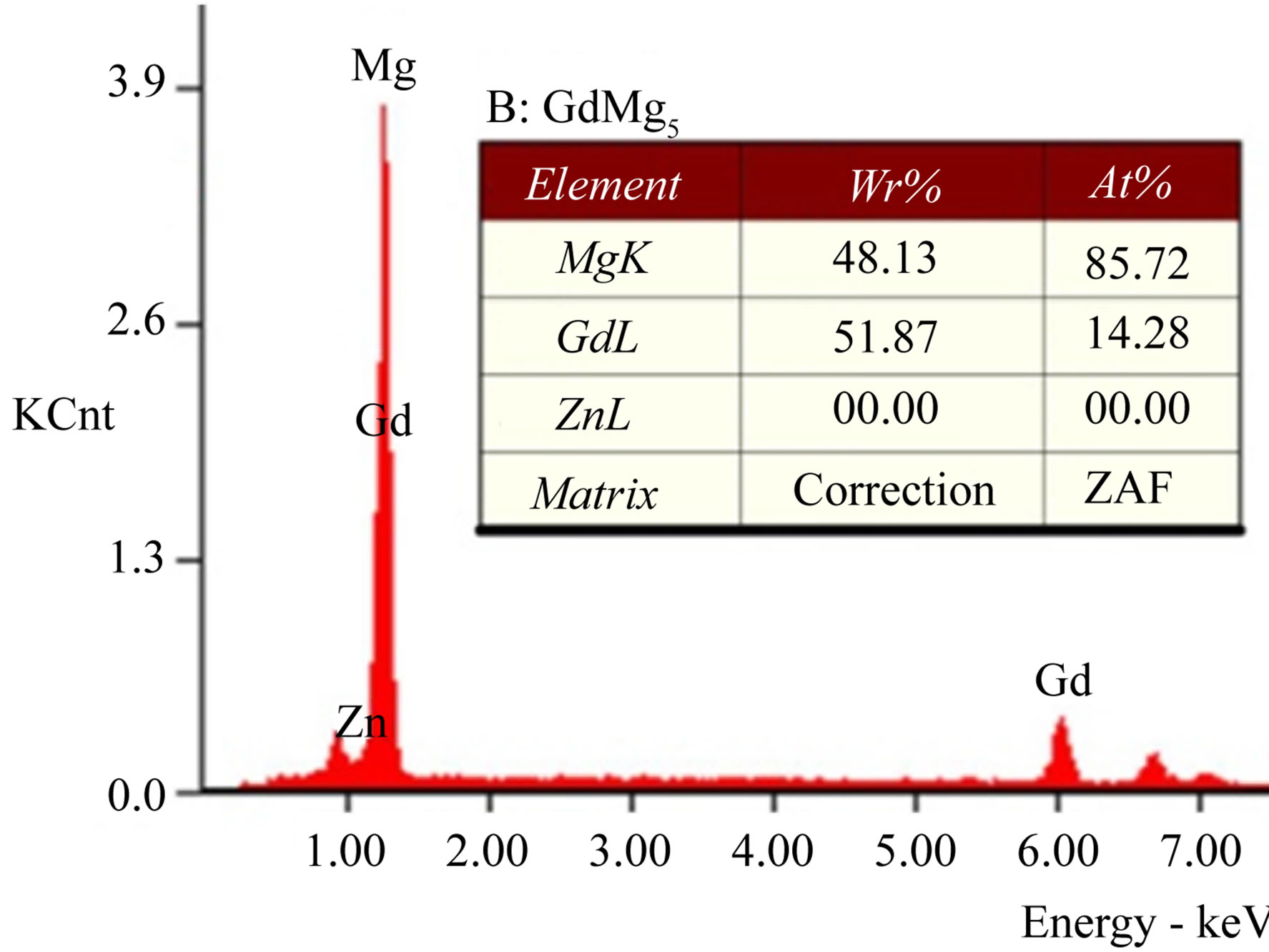
Figure 2. SEM images ((a) and (b)) of the GZ31 sheet and corresponding energy dispersive X-ray spectra of points A and B indicated in the image (a).
 (a)
(a)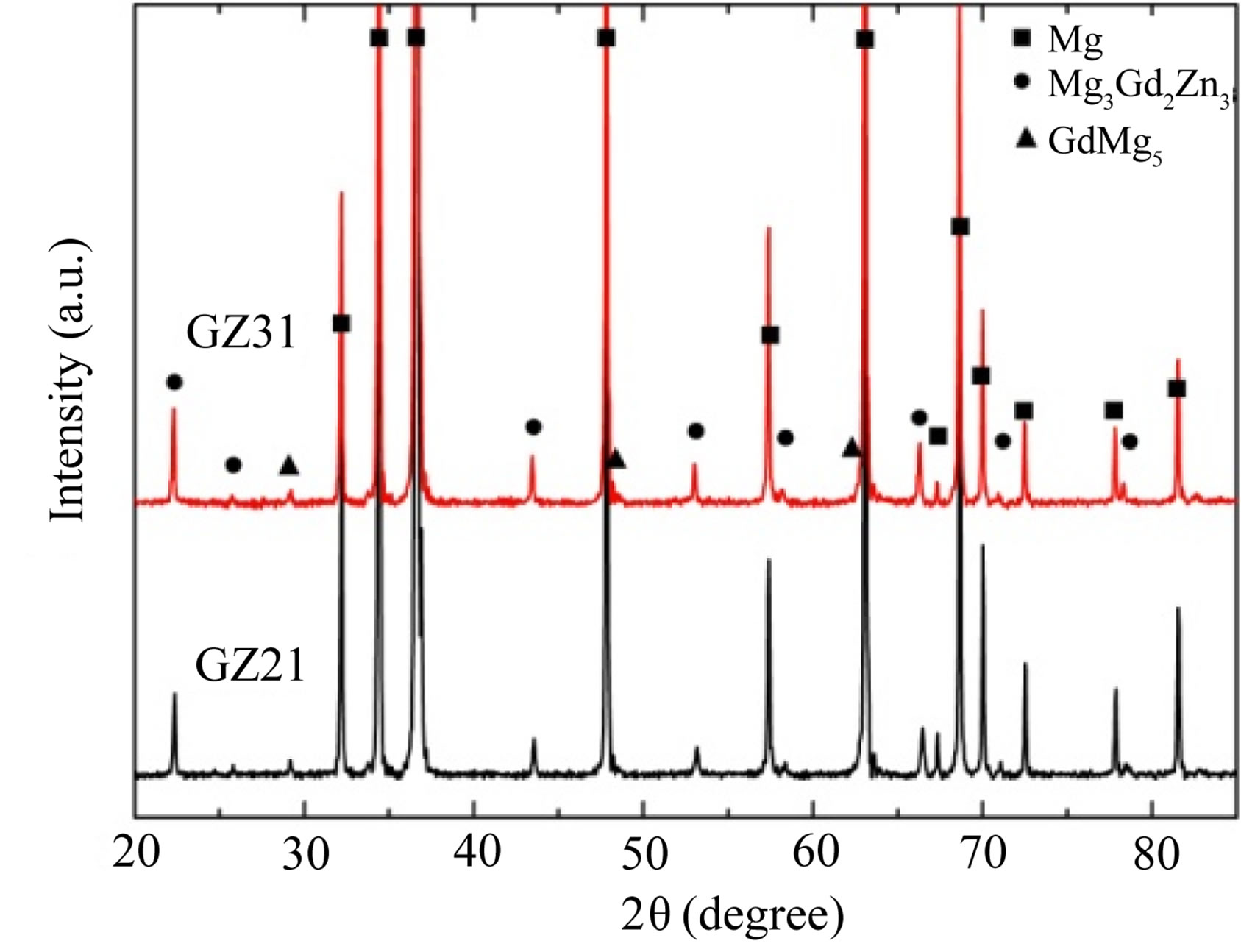 (b)
(b)
Figure 3. X-ray diffraction patterns of the rolled Mg-Zn-Gd sheets: (a) ZG11 and ZG21; (b) GZ21 and GZ31.
AZ31 alloy, the rolled AZ31 sheets were also tested (tension and compression) along the rolling direction in this study. The strain-stress curves were plotted in Figure 5(a). The tensile curves of the Mg-Zn-Gd samples display an abrupt yielding followed by a low hardening rate plateau. After that, a remarkable linear hardening at a plastic strain of roughly 3% is observed. It can be seen from Figure 5 that this is similar to the compression curves of the AZ31 sheet along the rolling direction, which was ascribed to a twining-dominated deformation [18]. However, the tensile flow curves of the AZ31 samples along the rolling direction exhibited a typical parabolic hardening behavior due to a slip-dominated deformation [20]. The tensile properties of the Mg-Zn-Gd and AZ31 sheets are summarized in Table 1. It can be seen that the ultimate elongations of the Mg-Zn-Gd sheets vary from
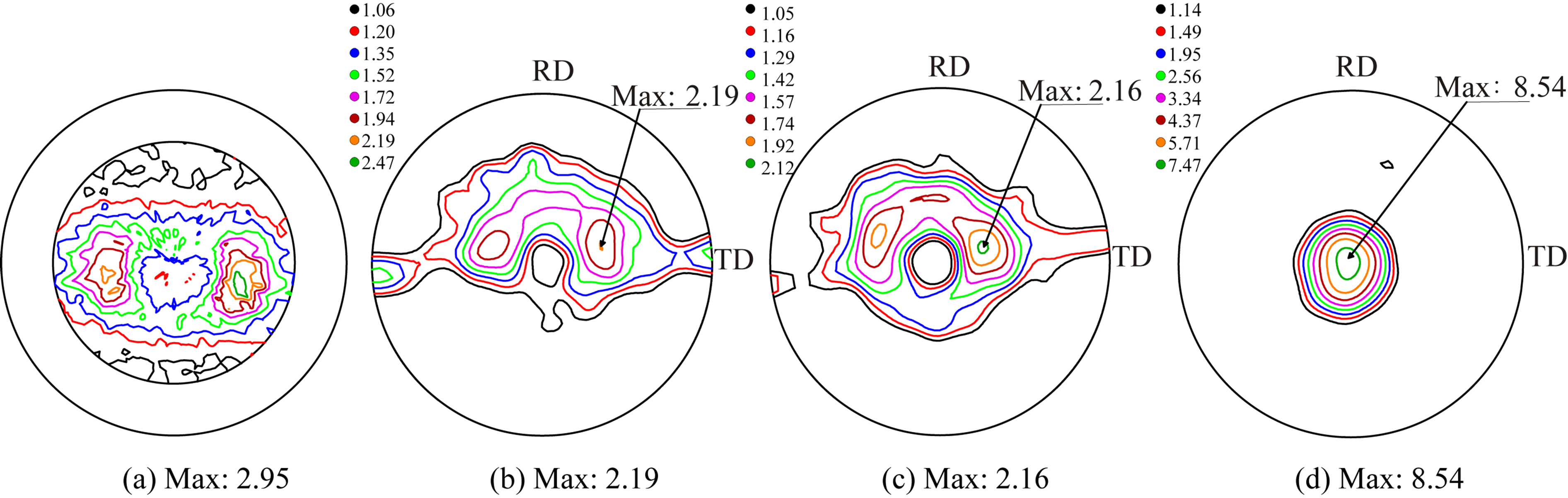
Figure 4. SEM images ((a) and (b)) of the GZ31 sheet and corresponding energy dispersive X-ray spectra of points A and B indicated in the image (a).
 (a)
(a)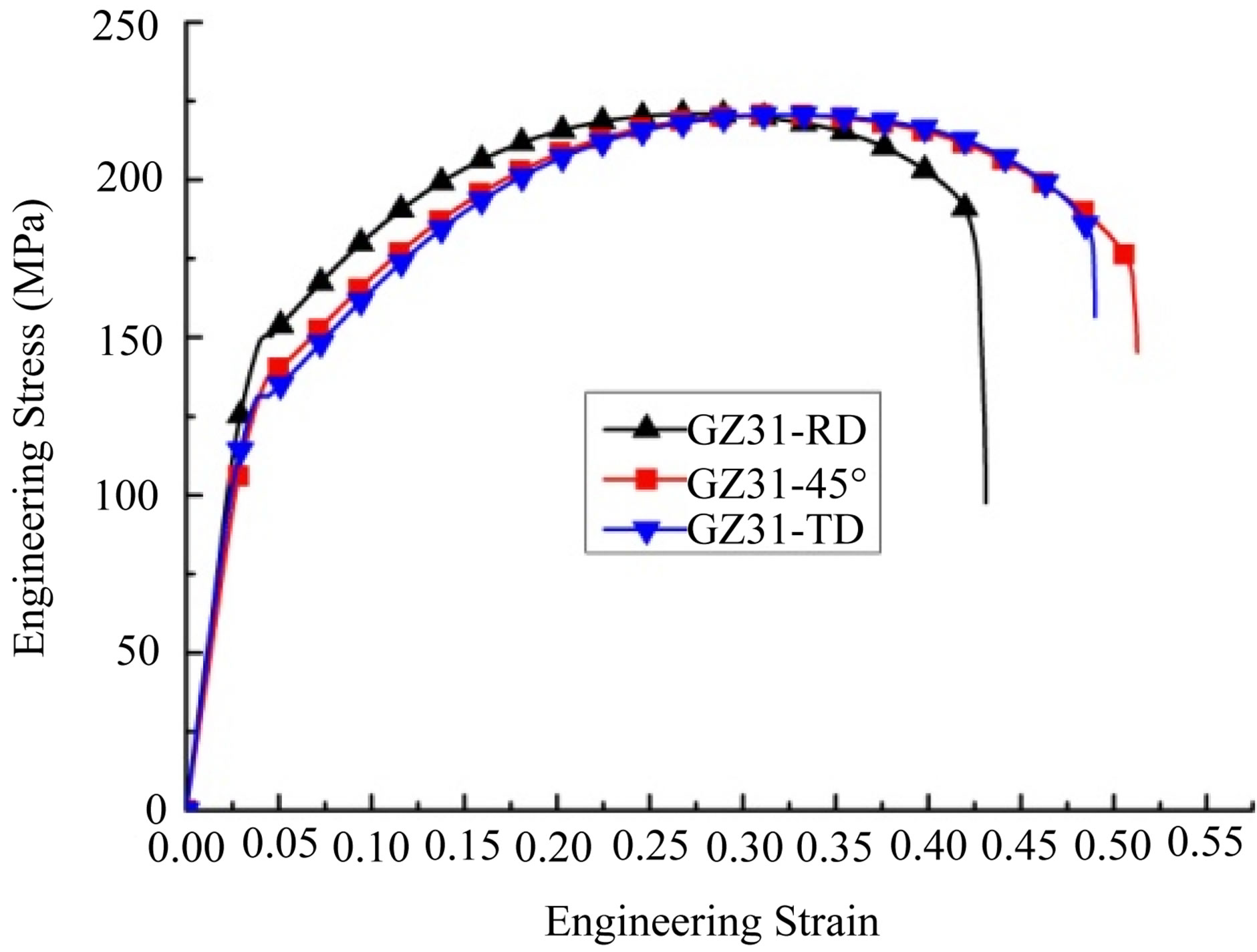 (b)
(b)
Figure 5. Typical tensile stress-strain curves of (a) the rolled ZG11 and ZG21 sheets in the tensile directions of RD, and (b) the rolled ZG31 sheet in the tensile directions of RD, 45˚ and TD.

Table 1. Room-temperature tensile properties of the rolled Mg-Zn-Gd sheets.
28% to 47% while that of the AZ31 alloy is no more than 23%. It should be noted that the elongation is greater along the TD than along the RD and the yield strength is reverse in these alloys. This is completely opposite to that of rolled AZ31 sheets [20].
It is known that the press formability of sheets at room temperature is strongly influenced by the Lankford value (r-value). The r-values for Mg-Zn-Gd alloys sheets were investigated by conducting tensile tests and the results are summarized in Table 2, where the data of the rolled AZ31 sheets are also listed for comparison [24]. The average r-value (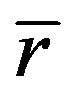 ) and the planar anisotropy of the rvalue (Δr) are expressed as [18]
) and the planar anisotropy of the rvalue (Δr) are expressed as [18]
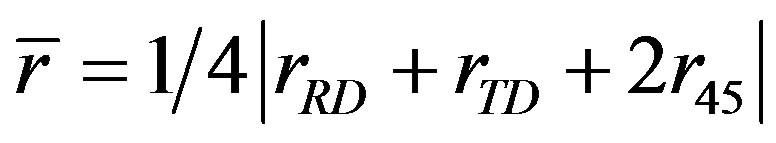 (1)
(1)
The average r-values of the Mg-Gd-Zn alloys ( = ~1) are much lower than that of the rolled AZ31 sheets [24]. The low r-value less than unity indicate that sheet thinning can easily occur during in-plane tensile deformation. Moreover, the r-value of rolled AZ31 sheets along different directions varied greatly, which would restrict the stretching capability [24]. In contrast, the r-values of the Mg-Gd-Zn sheets along different directions are close to 1.
= ~1) are much lower than that of the rolled AZ31 sheets [24]. The low r-value less than unity indicate that sheet thinning can easily occur during in-plane tensile deformation. Moreover, the r-value of rolled AZ31 sheets along different directions varied greatly, which would restrict the stretching capability [24]. In contrast, the r-values of the Mg-Gd-Zn sheets along different directions are close to 1.
The results of the Erichsen tests at room temperature are shown in Figures 6(a) and (b). The tensile elongation and stretch formability balance in the GZ21 and GZ31 sheets is shown in Figure 6(c), and the data for typical commercial Mg alloy and Al alloys are also included for comparison [25-28]. The Erichsen values of GZ31 alloy were a little larger than that of GZ21 alloy, which is consistent with the ductile results of uniaxial tensile test. However, the Erichsen values are only 2.6 and 4.1 at room temperature and 433 K for normally rolled AZ31 Mg alloy sheets with a grain size of 16 μm [25], and the Erichsen values at room temperature are also only ~4.0 for the Mg-Ce alloy and differential speed rolling processed AZ31 Mg alloy sheets with a modified and weakened basal texture [25,28]. Comparatively speaking, the Mg-Zn-Gd alloys exhibited excellent stretch formability (IE ~8), which is a match for that of 5000 and 6000 series Al alloy, of which are about 9 - 10 [26,27] and much better than that of AZ31 Mg alloy sheets.
3.2. On the Castability and Semi-Solid Formability of Mg-Al-Ca Alloys
3.2.1. Solidification Pathway of Mg-Al-Ca Alloys
The solidification pathways of Mg-Al-Ca alloys have been investigated by cooling curve thermal analysis. Figure 7 shows a typical cooling curve and its first derivative curve which are used to determine some critical points during solidification. The results show that the Cacontaining phase formation mainly depends on Ca content and Ca/Al ratio. With increasing the Ca/Al ratio

Table 2. Planar and in-plane anisotropy of the Mg-Gd-Zn sheets.

Figure 6. Specimens of the rolled Mg-Zn-Gd alloys after the Erichsen tests at room temperature: (a) GZ21, (b) GZ31, and relationships between tensile elongation (Elongation-tofailure) and stretch formability (Erichsen value) in the present alloys; the data for typical commercial Mg alloy and Al alloys are also included for comparison.
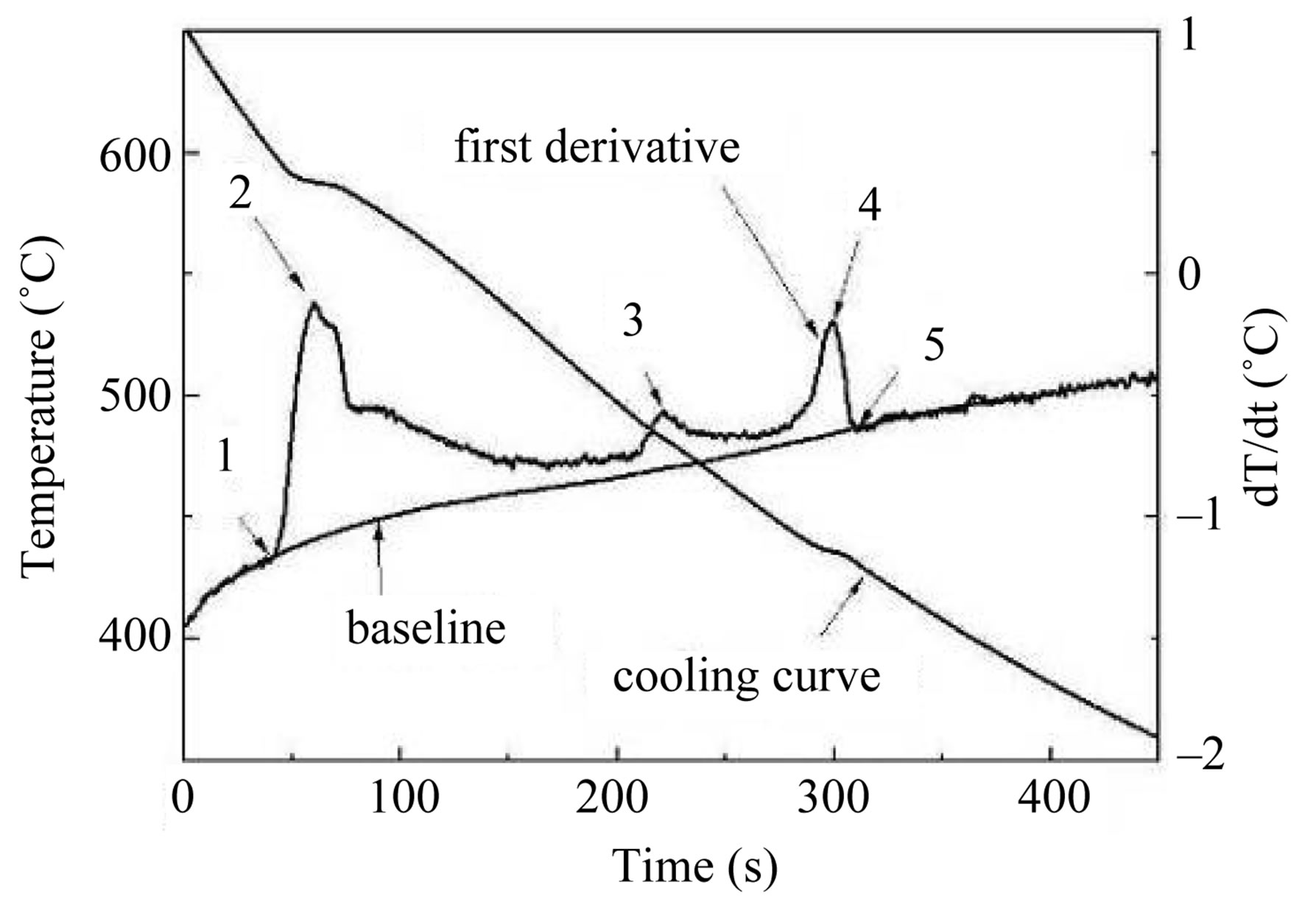
Figure 7. A typical cooling curve and its first derivative curve to determine the critical points during solidification. 1. Liquidus; 2. Maximum growth of primary α-Mg; 3. Ca containing phase formation; 4. Mg17Al12 phase formation; 5. Solidus.
these phases transform from Al2Ca to (Mg, Al)2Ca and Mg2Ca. Moreover, Ca addition decreases the liquidus temperature of Mg-Al alloys, but influences the solidus temperature in a more complex way. The experimentally determined vertical sections of AZX91x and AMX50x system are shown in Figure 8, which show clearly the liquidus, solidus temperature and secondary phase formation association with the calcium content during solidification.
3.2.2. Dendrite Coherency Point
The dendrite coherency point (DCP) defined for both a certain fraction solid fDCP and a certain temperature TDCP corresponds to the point of impingement of the dendrites where strength of the mush begins to develop [29]. The formation of microstructure and casting defects in die castings and permanent mold castings, such as dendrite size and morphology, hot tearing and porosity is suggested to be strongly dependent on dendrite coherency of the alloy which in turn depends on alloy composition and solidification conditions. Therefore, the knowledge of DCP is essential to eliminate hot tearing and to understand microstructure formation during semi-solid forming and conventional casting processes. Two-thermocouple thermal analysis method was applied to determine the dendrite coherency point in the present research [30]. The variation of the solid fraction corresponding to dendrite coherency (fDCP) as a function of Ca concentration is plotted in Figure 9. The fDCP value varies from 18 to 50 pct, and it decreases with increasing Ca addition in both series of alloys.
3.2.3. Deformation Behavior in the Semi-Solid State
The deformation behavior of alloys in the semi-solid state have been widely investigated due to their guidance to semi-solid metal processing and offering better understanding on the formation of hot tear. We carried out the compress test of AZX911 and AZX912 alloy at 515˚C and 530˚C, which are in the mushy zone (i.e. the temperature between dendrite coherency point and solidus temperature) of these two alloys. Figure 10 shows that AZX912 alloy exhibits much higher peak stress than AZX911 alloy both at 515˚C and 530˚C, even though at 530˚C, the solid fraction in AZX911 alloy is higher than that in AZX912 alloy.
The stress-based criteria are widely used to evaluate the hot tearing susceptibility of an alloy [31]. These criteria are based on the viewpoint that a semisolid body will fracture if the applied or induced stress exceeds the strength of the body. According to these criteria, the alloys having higher strength in the semi-solid state should present lower hot tearing susceptibility. In contrast to the stress-based criteria, it is reported that the introduction of Ca addition could increase the hot tearing
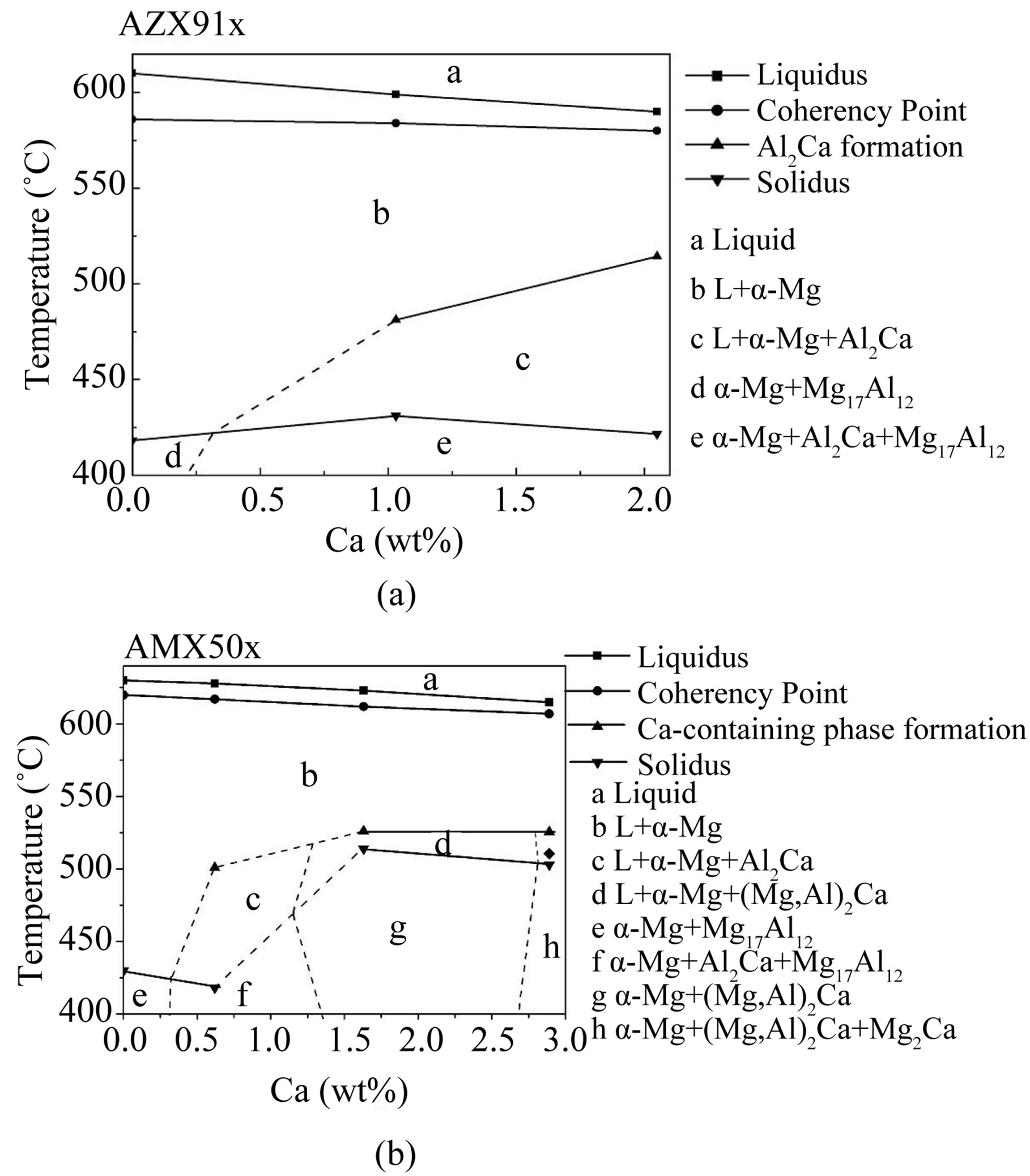
Figure 8. Solidification pathways of Mg-Al-Ca alloys: (a) for AZX91x and (b) for AMX50x. The broken lines mean some uncertainty for the border of the characteristic lines and regions.

Figure 9. The effect of Ca concentration on solid fraction at dendrite coherency point.

Figure 10. Maximum stress vs. strain rate in a log-log diagram.
susceptibility of AZ91 [14] and AM50 [10], but when the Ca level was higher than 2 wt% in AM50, the problem of hot tearing significantly reduced [10]. Based on the feeding mechanisms for casting proposed by Campbell [30] and recently developed by Dahle et al. [32], lower fDCP value means that mass feeding finishes and interdendrite feeding starts to dominate at a higher liquid fraction. Therefore, we proposed that the formation of Al2Ca between the DCP and solidus temperature may block the liquid feeding at the last stage of solidification, thus produce hot tears.
3.2.4. Thermodynamic Prediction of Semi-Solid Formability of Mg-Al-Ca Alloys
To overcome the hot crack problem of Mg-Al-Ca alloys in traditional casting process like diecasting, semi-solid metal (SSM) processing is an alternative. Thermodynamic calculation provides us with a useful tool for alloy composition selection for semi-solid forming. A two-stage thermodynamic model [33] was applied to simulate the solidification of Mg-Al-Ca alloys during SSM processing. The two-stage thermodynamic model assumes that the magnesium alloy slurry should be in the equilibrium state at the barrel before injection, and solidify according to the Scheil equation after being injected into the mold. As SSM processing of magnesium alloys is often performed at relatively high liquid fraction, i.e. relatively high temperature, combining the intensive shearing before injection in thixomolding or/and rheodiecasting, the slurry tends to reach equilibrium. After being injected into the mold, the material cools with a high solidification rate, thus the Scheil equation solidification assumption is also acceptable.
Based on the two-stage thermodynamic model, several parameters, such as Temperature sensitivity of liquid fraction (dfL/dT), Solidification range (TSS-S), The highest “knee” referred to as the point occurring between 30% and 50% liquid on the liquid fraction vs. temperature curve, have been chosen to evaluate the SSM processability of Mg-Al-Ca alloys. Figure 11 shows the potential alloy compositions selected for SSM processing based on two stage thermodynamic calculations in the Mg-rich corner of the Mg-Al-Ca systems. It can be seen that the alloys with composition located inside the dot line satisfy not only the “knee” rule, but also the other two criteria, and thus have potential for semi-solid forming.
4. Conclusions
1) The rolled Mg-Zn-Gd alloys have fine recrystallized microstructures with a large amount of tiny particles homogeneously distributed in the matrix.
2) The Mg-Zn-Gd sheets have an oval-shaped distribution of basal poles at angles of about 30˚ to normal direction (ND) of the sheets, and it seems that the basal
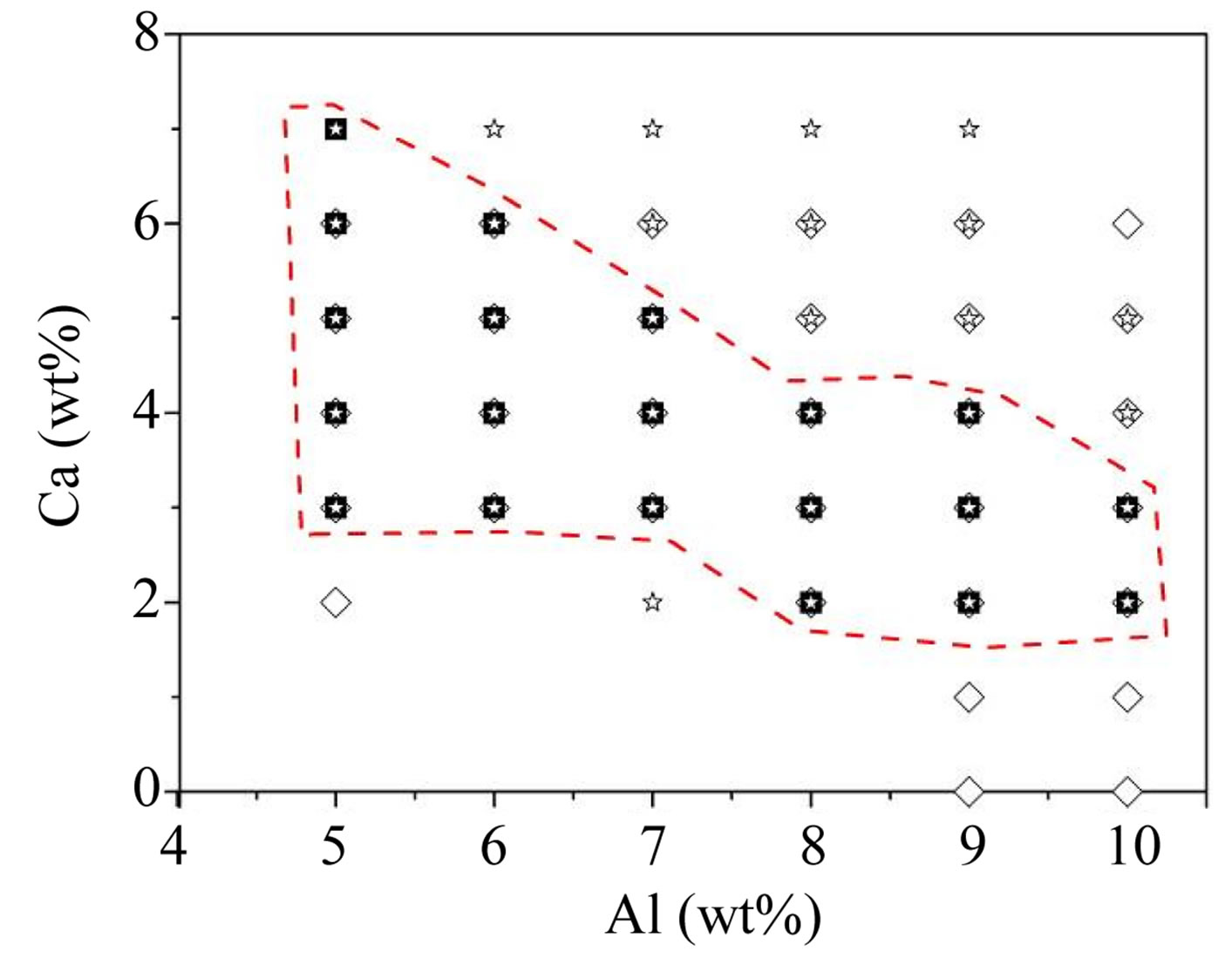
Figure 11. Promising alloy compositions selected for SSM processing (at fL = 0.7) based on the two-stage thermodynamic calculations. ☆ satisfying dfL/dT |fL=0.7 ≤ 0.015, ◇ satisfying 10 ˚C ≤ ΔTSS-S ≤ 150 ˚C, ■ satisfying the “Knee” rule.
texture intensity is effectively weakened by addition of Gd.
3) The sheets exhibit a large elongation-to-failure (nearly 50%), uniform elongation (larger than 30%) and a high Erichsen values (nearly 8) at room temperature, due to the excellent strain hardening capability and low r value.
4) The solidification pathways of Mg-Al-Ca alloys are obtained. The liquidus temperature decreases with increasing Ca content, while the solidus temperature and secondary phases formation are greatly affected by Ca content and Ca/Al ratio.
5) The hot tearing susceptibility of Mg-Al-Ca alloys is associated with the formation of Al2Ca phases after dendrite coherency point.
6) Thermodynamic calculation is a useful tool to evaluate the semisolid formability of alloys. A potential alloy composition range of Mg-Al-Ca alloys amenable to semisolid forming is predicted.
REFERENCES
- T. Mukai, M. Yamanoi, H. Watanabe and K. Higashi, “Ductility Enhancement in AZ31 Magnesium Alloy by Controlling Its Grain Structure,” Scripta Materialia, Vol. 45, No. 1, 2001, pp. 89-94. doi:10.1016/S1359-6462(01)00996-4
- R. Gehrmann, M. M. Frommert and G. Gottstein, “Texture Effects on Plastic Deformation of Magnesium,” Materials Science and Engineering: A, Vol. 395, No. 1-2, 2005, pp. 338-349. doi:10.1016/j.msea.2005.01.002
- Y. Chino, J.-S. Lee, K. Sassa, A. Kamiya and M. Mabuchi, “Press Formability of a Rolled AZ31 Mg Alloy Sheet with Controlled Texture,” Materials Letters, Vol. 60, No. 2, 2006, pp. 173-176. doi:10.1016/j.matlet.2005.08.012
- N. Stanford, D. Atwell and M. R. Barnett, “The Effect of Gd on the Recrystallisation, Texture and Deformation Behaviour of Magnesium-Based Alloys,” Acta Materialia, Vol. 58, No. 20, 2010, pp. 6773-6783. doi:10.1016/j.actamat.2010.09.003
- S. Sandlöbes, S. Zaefferer, I. Schestakow, S. Yi and R. Gonzalez-Martinez, “On the Role of Non-Basal Deformation Mechanisms for the Ductility of Mg and Mg-Y Alloys,” Acta Materialia, Vol. 59, No. 2, 2011, pp. 429-439. doi:10.1016/j.actamat.2010.08.031
- Y. Chino, K. Sassa and M. Mabuchi, “Tensile Properties and Stretch Formability of Mg-1.5 mass%Zn-0.2 mass%Ce Sheet Rolled at 723K,” Materials Transactions, Vol. 49, No. 7, 2008, pp. 1710-1712. doi:10.2320/matertrans.MEP2008136
- Y. Chino, K. Sassa and M. Mabuchi, “Texture and Stretch Formability of Mg-1.5 mass%Zn-0.2 mass%Ce Alloy Rolled at Different Rolling Temperature,” Materials Transactions, Vol. 49, No. 12, 2008, pp. 2916-2918. doi:10.2320/matertrans.MEP2008257
- Y. Chino, K. Sassa and M. Mabuchi, “Texture and Stretch Formability of a Rolled Mg-Zn Alloy Containing Dilute Content of Y,” Materials Science and Engineering: A, Vol. 513-514, No. 1, 2009, pp. 394-400. doi:10.1016/j.msea.2009.01.074
- H. Yan, R. S. Chen and E. H. Han, “Room-Temperature Ductility and Anisotropy of Two Rolled Mg-Zn-Gd Alloys,” Materials Science and Engineering: A, Vol. 527, No. 15, 2010, pp. 3317-3322. doi:10.1016/j.msea.2010.02.038
- A. A. Luo, “Recent Magnesium Alloy Development for Elevated Temperature Applications,” International Materials Reviews, Vol. 49, No. 1, 2004, pp. 13-30. doi:10.1179/095066004225010497
- S.-H. Ha, J.-K. Lee, H.-H. Jo, S.-B. Jung and S. K. Kim, “Behavior of CaO and Calcium in pure Magnesium,” Rare Metals, Vol. 25, No. 6, 2006, pp. 150-154. doi:10.1016/S1001-0521(08)60071-6
- Y. Terada, D. Itoh and T. Sato, “Creep Rupture Properties of Die-Cast Mg-Al-Ca Alloys,” Materials Chemistry and Physics, Vol. 113, No. 2-3, 2009, pp. 503-506. doi:10.1016/j.matchemphys.2008.09.015
- A. A. Luo, B. R. Powell and M. P. Balogh, “Creep and Microstructure of Magnesium-Aluminum-Calcium Based Alloys,” Metallurgical and Materials Transactions A, Vol. 33, No. 3, 2002, pp. 567-574. doi:10.1007/s11661-002-0118-1
- B. Tang, S.-S. Li, X.-S. Wang, D.-B. Zeng and R. Wu, “Effect of Ca/Sr Composite Addition into AZ91D Alloy on Hot-Crack Mechanism,” Scripta Materialia, Vol. 53, No. 9, 2005, pp. 1077-1082. doi:10.1016/j.scriptamat.2005.06.039
- J. O. Andersson, T. Helander, L. Höglund, P. Shi and B. Sundman, “Thermo-Calc & DICTRA, Computational Tools for Materials Science,” Calphad, Vol. 26, No. 2, 2002, pp. 273-312. doi:10.1016/S0364-5916(02)00037-8
- Y. Zhong, “Investigation in Mg-Al-Ca-Sr-Zn System by Computational Thermodynamics Approach Coupled with First-Principles Energetics and Experiments,” Ph.D. Thesis, the Pennsylvania State University, University Park, 2005.
- Y. Liu, G. Yuan, S. Zhang, X. Zhang, C. Lu and W. Ding, “Effects of Zn/Gd Ratio and Content of Zn, Gd on Phase Constitutions of Mg Alloys,” Materials Transactions, Vol. 49, No. 5, 2008, pp. 941-944. doi:10.2320/matertrans.MC200767
- Z. P. Luo and H. Hashimoto, “High-Resolution Electron Microscopy Observation of a New Crystalline Approximant W’ of Mg-Zn-Y Icosahedral Quasicrystal,” Micron, Vol. 31, No. 5, 2000, pp. 487-492. doi:10.1016/S0968-4328(99)00128-6
- N. Stanford and M. R. Barnett, “The Origin of ‘Rare Earth’ Texture Development in Extruded Mg-Based Alloys and Its Effect on Tensile Ductility,” Materials Science and Engineering: A, Vol. 496, No. 1-2, 2008, pp. 399-408. doi:10.1016/j.msea.2008.05.045
- J. Bohlen, M. R. Nurnberg, J. W. Senn, D. Letzig and S. R. Agnew, “The Texture and Anisotropy of MagnesiumZinc-Rare Earth Alloy Sheets,” Acta Materialia, Vol. 57, No. 6, 2007, pp. 2101-2112. doi:10.1016/j.actamat.2006.11.013
- M. R. Barnett, M. D. Naveaa and C. J. Bettles, “Deformation Microstructures and Textures of Some Cold Rolled Mg Alloys,” Materials Science and Engineering: A, Vol. 386, No. 1-2, 2004, pp. 205-211. doi:10.1016/j.msea.2004.07.030
- F. Kaiser, D. Letzig, J. Bohlen, A. Styczynski, Ch. Hartig and K. U. Kainer, “Anisotropic Properties of Magnesium Sheet AZ31,” Materials Science Forum, Vol. 419-422, No. 1, 2003, pp. 315-320. doi:10.4028/www.scientific.net/MSF.419-422.315
- X. Huang, K. Suzuki, A. Watazu, I. Shigematsu and N. Saito, “Mechanical Properties of Mg-Al-Zn Alloy with a Tilted Basal Texture Obtained by Differential Speed Rolling,” Materials Science and Engineering: A, Vol. 488, No. 1-2, 2008, pp. 214-220. doi:10.1016/j.msea.2007.11.029
- Y. Chino and M. Mabuchi, “Enhanced Stretch Formability of Mg-Al-Zn Alloy Sheets Rolled at High Temperature (723 K),” Scripta Materialia, Vol. 60, No. 6, 2009, pp. 447-450. doi:10.1016/j.scriptamat.2008.11.029
- X. Huang, K. Suzuki, A. Watazu, I. Shigematsu and N. Saito, “Improvement of Formability of Mg-Al-Zn Alloy Sheet at Low Temperatures Using Differential Speed Rolling,” Journal of Alloys and Compounds, Vol. 470, No. 1-2, 2009, pp. 263-268. doi:10.1016/j.jallcom.2008.02.029
- Japan Light Metal Association, “Aluminum Handbook,” Japan Light Metal Association, Tokyo, 2000.
- M. Sugamata, J. Kaneko and M. Numa, “Evaluation of Formability of Light Metal Sheets at High Temperatures by Conical Cup and Erichsen Tests,” Journal of the Japan Society for Technology of Plasticity, Vol. 41, No. 470, 2000, pp. 233-238. doi:j-east/article/200011/000020001100A0402883
- Y. Chino, M. Kado and M. Mabuchi, “Enhancement of Tensile Ductility and Stretch Formability of Magnesium by Addition of 0.2 wt%(0.035 at%)Ce,” Materials Science and Engineering: A, Vol. 494, No. 1-2, 2008, pp. 343-349. doi:10.1016/j.msea.2008.04.059
- A. K. Dahle and L. Arnberg, “Development of Strength in Solidifying Aluminium Alloys,” Acta Materialia, Vol. 45, No. 2, 1997, pp. 547-559. doi:10.1016/S1359-6454(96)00203-0
- S. M. Liang, R. S. Chen, J. J. Blandin, M. Suery and E. H. Han, “Thermal Analysis and Solidification Pathways of Mg-Al-Ca System Alloys,” Materials Science and Engineering: A, Vol. 480, No. 1-2, 2008, pp. 365-372. doi:10.1016/j.msea.2007.07.025
- D. G. Eskin, Suyitno and L. Katgerman, “Mechanical Properties in the Semi-Solid State and Hot Tearing of Aluminium Alloys,” Progress in Materials Science, Vol. 49, No. 5, 2004, pp. 629-711. doi:10.1016/S0079-6425(03)00037-9
- A. K. Dahle, Y. C. Lee, M. D. Nave, P. L. Schaffer and D. H. StJohn, “Development of the As-Cast Microstructure in Magnesium-Aluminium Alloys,” Journal of Light Metals, Vol. 1, No. 1, 2001, pp. 61-72. doi:10.1016/S1471-5317(00)00007-9
- M. B. Djurdjevic and R. Schmid-Fetzer, “Thermodynamic Calculation as a Tool For Thixoforming Alloy and Process Development,” Materials Science and Engineering: A, Vol. 417, No. 1-2, 2006, pp. 24-33. doi:10.1016/j.msea.2005.08.227
NOTES
*Corresponding author.

