Open Journal of Inorganic Non-metallic Materials
Vol.4 No.1(2014), Article ID:41183,5 pages DOI:10.4236/ojinm.2014.41002
The Surface Fractal Structure of Fish Scales
Department of Physics, Azerbaijan Technical University, Baku, Azerbaijan
Email: geldar-04@mail.ru
Copyright © 2014 Godzhaev Eldar et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Godzhaev Eldar et al. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received August 23, 2013; revised September 30, 2013; accepted October 7, 2013
Fractals; Scales; Fragments; Aggregation; ChannelsABSTRACT
By atomic force, microscopy studied the morphology of the surface of the scale of the Caspian Kutum. Analysis of the structure of channels of sensory systems showed that the nanostructures are not only fractal, but also self-similar. Fractal trajectories originate from the primary nucleus and extend to the sprawling low-density structure radically outwards scales like Lichtenberg figures. However, in contrast to the figures, Lichtenberg fractal band scales of fish each year are surrounded by concentric threads. The most likely mechanism for the formation of structural self-organization on the surface of the scales can be a model Witten-Sander.
1. Introduction
Similarity of the surface structures, some biological objects with fractals, is a very interesting fact in itself. Language “fractal geometry” can be extremely useful to the description of certain biological objects of living beings. For example, the shape of the lateral line of the fish is very convenient to describe a fractal language according to [1-3]. This approach can be very rewarding. It is known that the bodies of the lateral line of the fish carry a distinct mechanoreceptor function. Actually all known physical and chemical and biotic configurations arising in a reservoir, are accepted by tools of well-developed sensory systems of fish. The essential role in behavior of fishes is played with sense organs—the lateral line, or seismotouch system. It unites all sensitive receptor cells of shift which can be met in various sites of a body and the head [3,4]. The fishes catch earthquake before the most sensitive devices [4]. Live organisms including bodies of fishes look “expedient” (adapted for living conditions) simply because they die of inadaptation [2,3]. Studying morphology scales of fishes by a method of the atomic power microscopy (APM) would bring a certain clarity in distribution of touch channels.
The aim of the work was to identify the nature of the morphological features of the surface structures of the fish scales (for example, Kutum) by optical and atomic force microscopy (AFM).
2. Experiment and Discussion
The technique of research surface scales with AFM images in 2D and 3D is given in work [5]. Kutum’s lateral line represents a certain channel, which passes along all ridge, it begins from the head and comes to the end only at a tail. All surface consists of the weight of sensitive sensors which are connected with external receptors, located on scales and the nervous terminations of the fish. Sensitive cages of receptors of bodies of the studied objects of the lateral line form the isolated clusters in skin, but more often they are found through some intervals in fillets or channels in scales. The channels are completely closed depressions in the skin, or are in the form of open fractal grooves. Scale channels are filled with slime that promoted by porous and fractal character of morphology of this surface. Sensitive cells of the lateral line are collected in kidney-shaped groups and hidden to channels on scales of fishes who are washed by water. Removed on an optical microscope (OP) the morphology of a surface is given in figures 1 and 2. The fragments of year rings on a surface scales from under the first fin, touch channels, pictures with a optic microscope are given in Figures 3 and 4. OP-images of scales under the top fin connected with annual rings are given in Figure 5. AFM fragments of nanodistributions round year rings of fish Kutum were considered in Figures 6-9. During AFM investigations mucus from the surface of scales was washed off with water. Some characteristics of morphology are clearly visible: growth of branching on scale begins with a certain place not being in the scales center, but is closer to its edge watched in Figures 8 and 9. Growth dynamics of the surface areas can be considered as a special case of aggregation model that is suitable for describing the growth surface for biological systems.

Figure 1. Morphology of a surface of scales of the Caspian Kutum. Vertical lines proceeding from the center of scales noted nanogrooves (channels) in which liquids of special structure are shipped. In the depth of these channels pass the nervous terminations on which various signals are transmitted.
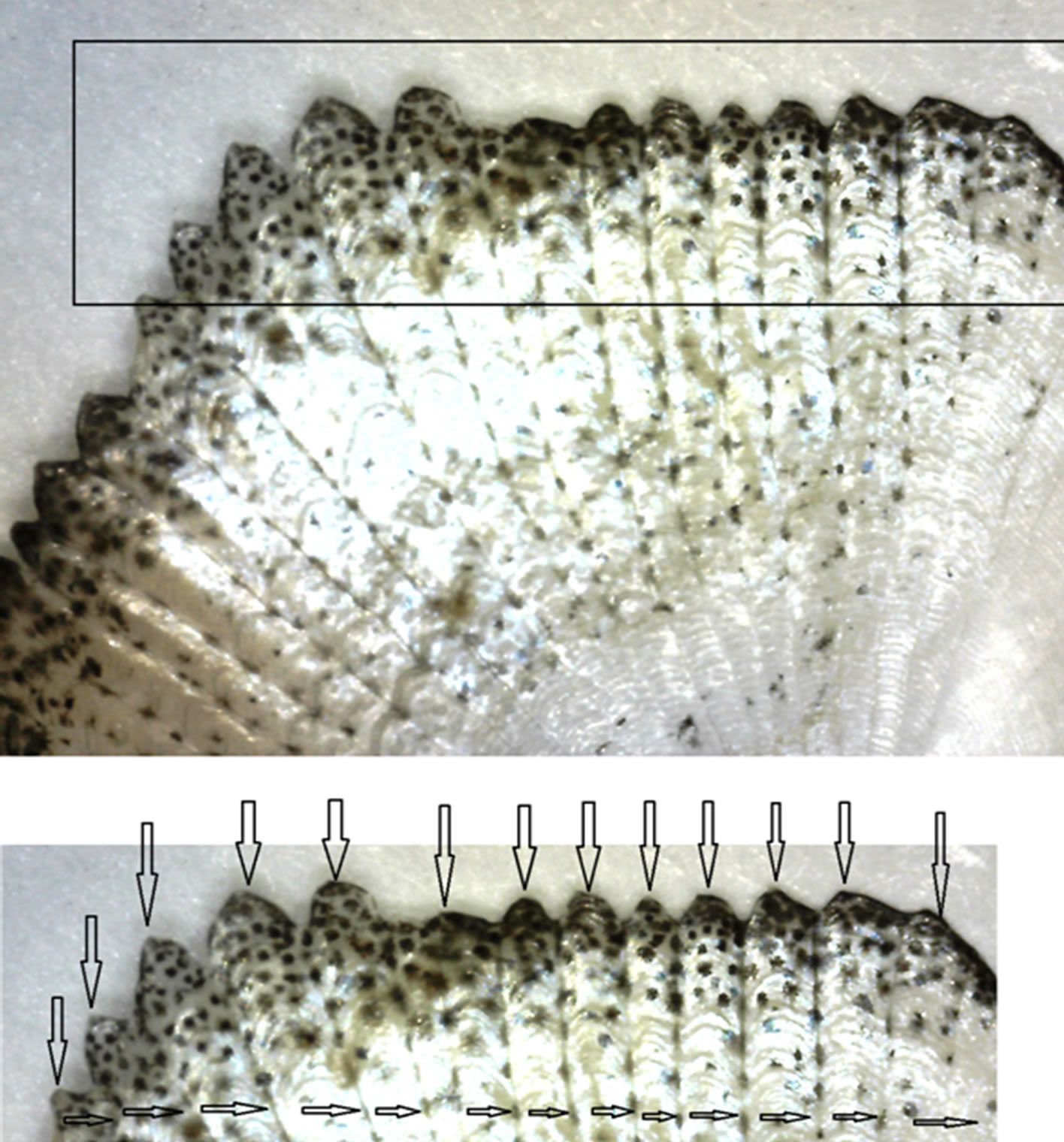
Figure 2. Fragments of the optical images of the scales of Kutum. The upper and lower fragments marked fractal outputs of the individual bands on the surface (the boundary marked by horizontal bands, and the vertical arrows marked zigzag shaped strips, in output).

Figure 3. The photo made by an optical microscope of a surface of scales of Kutum. By the bottom arrow (No. 5) it is specified (an ellipsoidal form) the main channel in the scales center. From this channel in the radial direction strips (2 - 4, 7-creep away 8). From below in skin of fish they are connected with the nervous terminations transmitting certain signals to the think-tank. Thus, the main fragments of the sensory system are special channels on the scales of fish.

Figure 4. Morphology of the central part of a lateral surface of scales of Kutum. The bottom big arrow defines location of the lateral line. In figure 1 they are noticeable as dashed lines). Between two horizontal shooters fragments of the rarefied structures with cross channels above are allocated. The same cross channels (it not annual Rings) are noted by horizontal shooters (on the right drawing). In the left from below the arrow noted thinner small radial structures of the line. They carry out a role of touch systems located on a scales surface.
Lines stretching from grain to edges of scales can be described by model of Witten-Sander [6-8]. Active surface in the course of growth the lines on it similar lightnings at the description across Witten-Sandra has absolutely other structure, than in Eden’s model [7]. This distinction reflects an essential role of diffusion and is shown that clusters in model of Witten-Sander externally look

Figure 5. Morphology of a surface of OP of scales, with Kutum’s allocated annual rings.

Figure 6. AFM fragment—images in 3D—the scale of a surface of scales of Kutum: through channels (they are noted by longitudinal lines) carry out communication from the head to a tail. It also is a fragment of the coherent lateral line on a scales surface. Separate nanoislands are noted by vertical lines. The black line noted the aggregated nanostructures—bioclusters. (Scan size: 7 × 7 mkm).
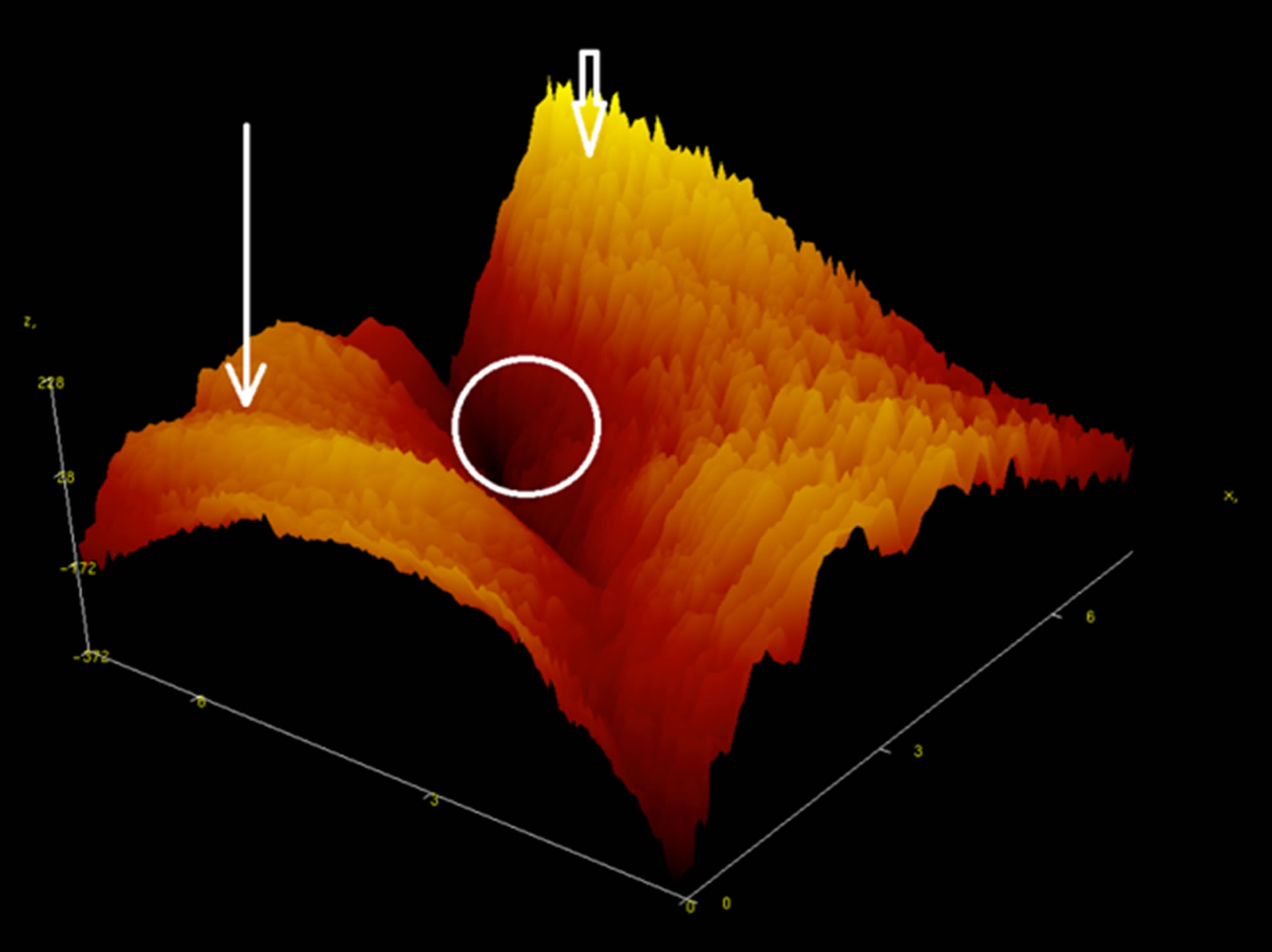
Figure 7. A fragment of the AFM image in 3-D-scale of the surface scales of the Caspian Kutum. In the center of nanopore allocated round the edges of the vertical arrows indicate the nanoprotrusions.
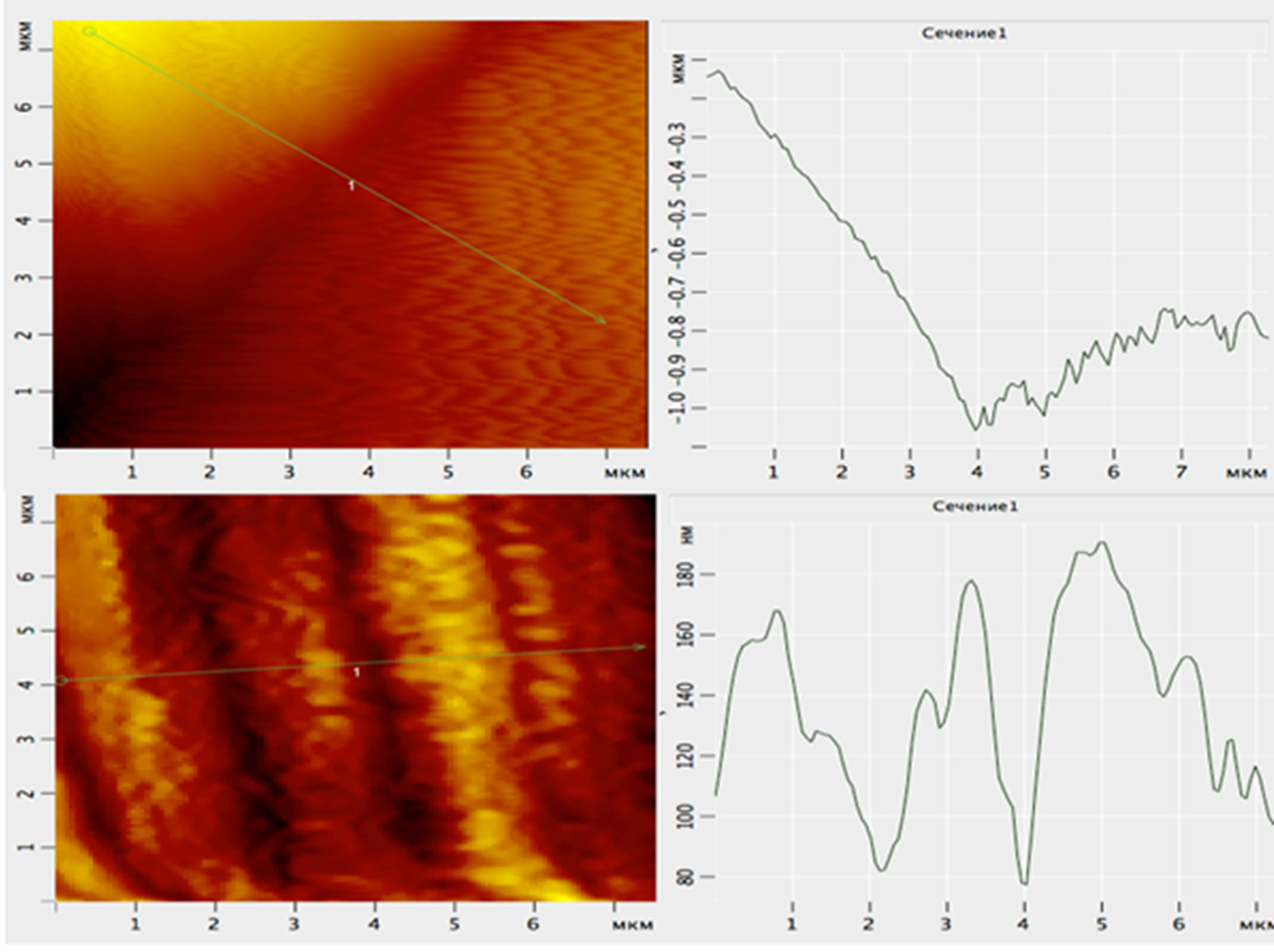
Figure 8. Longitudinal section of AFM—the image in 2D— the scale of a surface of scales of Kutum: pore sizes ranging ≈ 80-nm, the maximum height of structures within ≈ 100 nm.
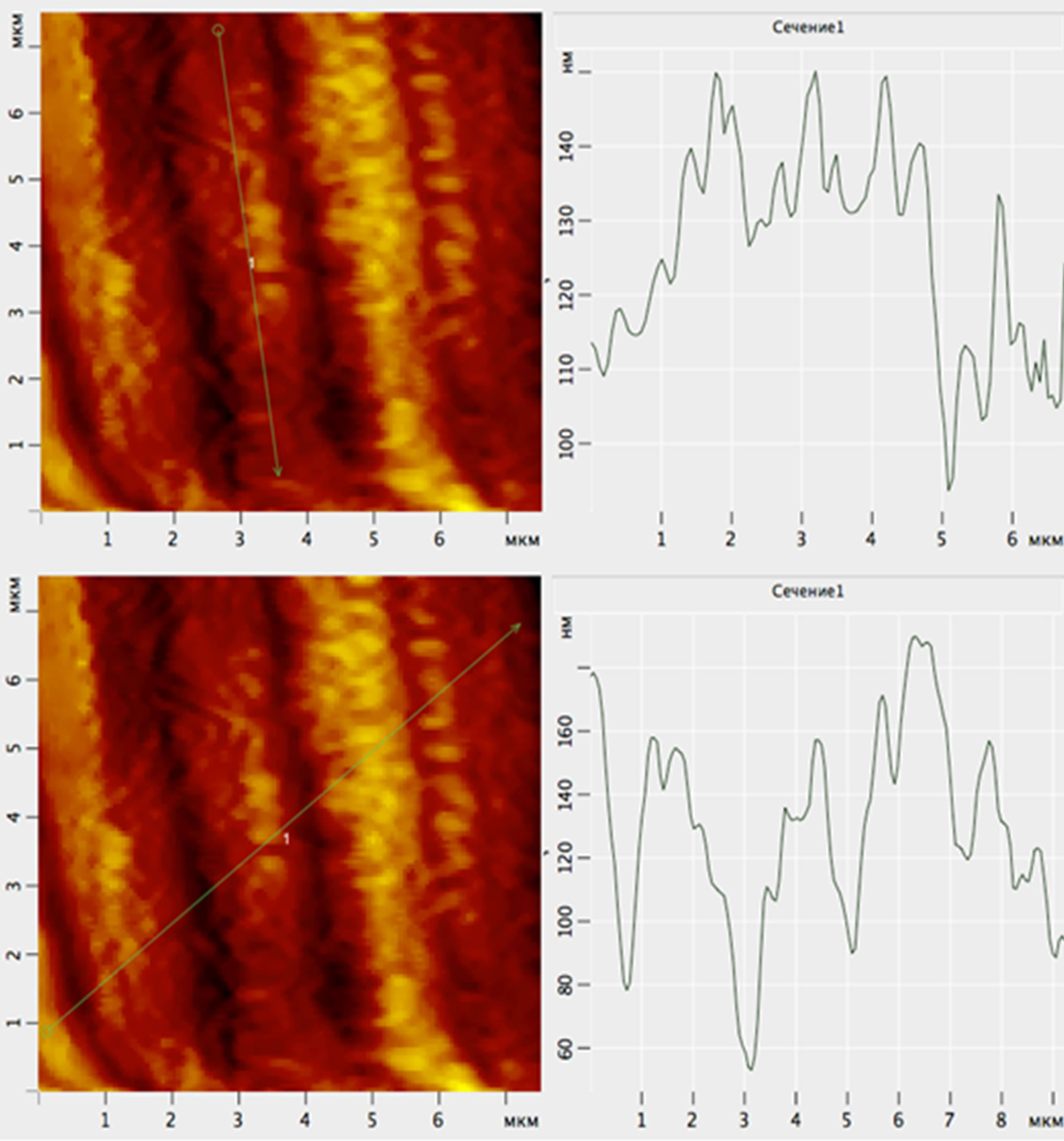
Figure 9. AFM image of the surface of the 2D—scale of the scales of Kutum: profilogram bottom surface of the channel shows its nano dimension: height of the bottom lines of scales ranging from 10 nm to 30 nm.
as fractals (see Figures 1-9). Ensembles of particles aggregating form larger objects with strongly branched rarefied structure, threadlike streams are thus formed, they are well visible in Figure 4. These threads as it is visible from AFM-images are the aggregated fractal clusters of the various sizes (see Figures 6-10).
On a surface of fish in information transfer nanodimensional channels of scales (them it is possible carry to touch sensors) have to play a leading role. In the presented fragments of OP—images in Figures 4 and 5
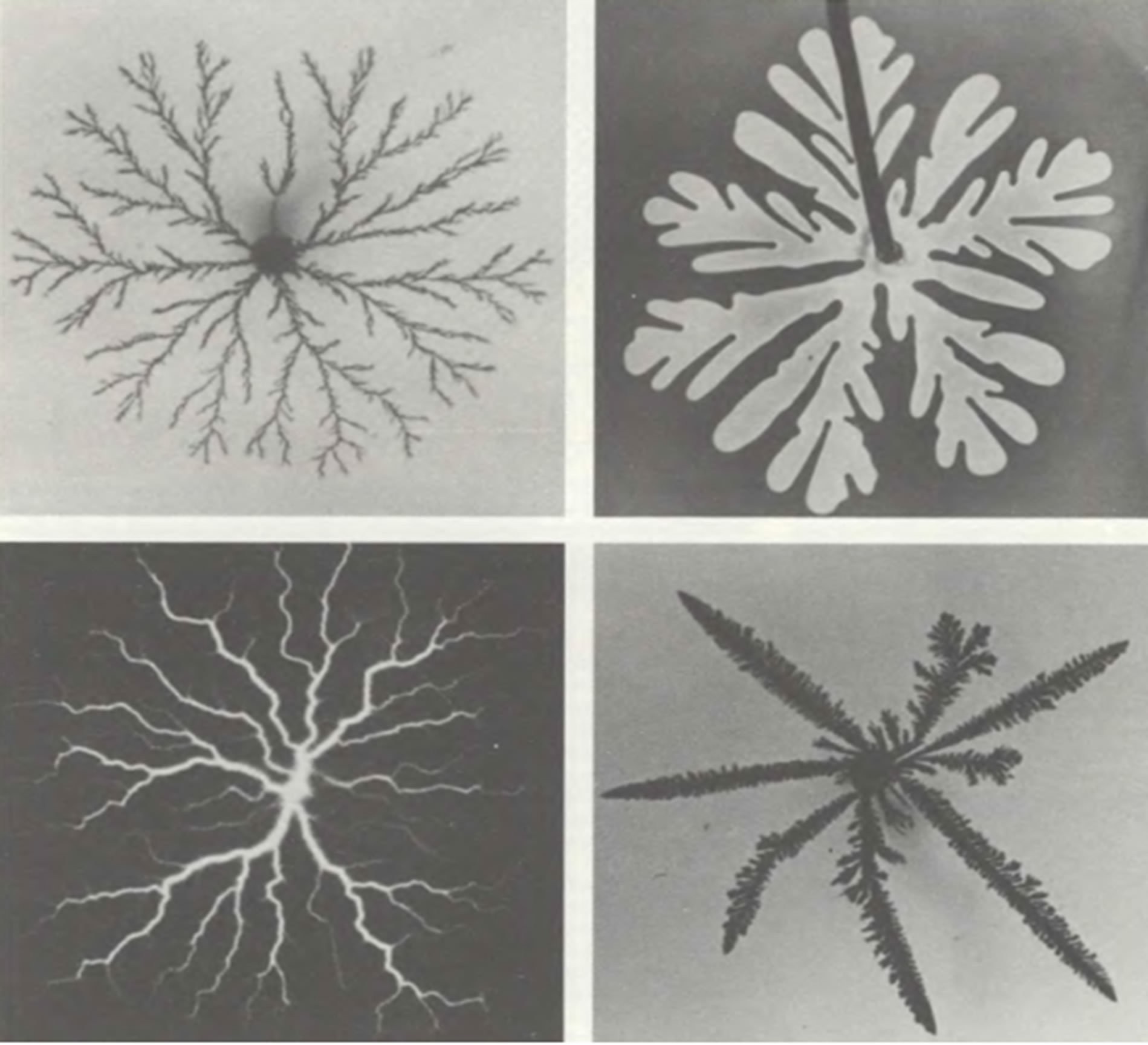
Figure 10. Fractals are generated as a result of the aggregation process of diffusion-limited [7]: the structure of the zinc deposited by electrolysis, the fractal dimension of the cluster is equal to 1.66. (top left), the “fingers” formed by air in glycerol (top right), and trace an electrical discharge, called a Lichtenberg figure (bottom left).
fragments of the lateral line passing on an external surface of scales, it are visible: longitudinal channel (Figures 4 and 5), under them sensitive cages, nerves. Scales containing channels are filled with liquid of specific ionic structure. In walls of channels as noted above pass the nervous terminations on which signals from environment are transmitted. As irritants of receptors water flows and low-frequency fluctuations of the environment serve. These OP-images are an example of observed macrofractal structures in the world of water inhabitants (fishes). It no wonder as dielectric substrates (what is scales of fishes) also possess the porous structural. All OP and AFM— images testify that Kutum possesses difficult system of touch channels which bodies (Figures 1-10) settle down on each side.
Each channel of scales represents, either an open fillet, or closed on all length, but having some separate exits. The structures investigated by us are located in skin and hypodermic bodies therefore they can be carried to touch system. Strips on both sides of a body from the head until the end of a tail fin are visually visible; it is part of touch sensors of fish. Appears more and more the facts of that fractal forms scale can be considered Kutum as the fractal structures known as percolation clusters, not arising when passing liquid through firm porous bodies, and at infiltration of fish through dense water. In works [6,7] the mechanism of fractal growth which called the aggregation limited by diffusion is offered. According to this model, a certain version of fractal objects can be received in the course of disorder irreversible growth. The putforward theory is attractive in two relations. First, it is simple and easily gives in to modeling on the computer. Secondly, and it is more important, it seems to explain how species of creeping-away fractal objects in scales in actual practice in the course of evolution could be formed. Each part of the fractal, shown in (Figures 1-10) consists of identical elements of the smaller size. In turn these parts can be united in even big objects with the same structure etc. Each “generation” comprises openings, on scale corresponding to the sizes of this generation. It is possible to call such drawing invariant in relation to scale. At each level any part of structure with a diameter, smaller diameter whole, looks in the same way, as well as whole. Invariancy in relation to scale is as though property of “symmetry” of fractal objects of fishes. Though process of the aggregation limited by diffusion, easily gives in to the description and modeling, we still insufficiently well understand it at deeper level, especially in relation to biological objects. However in qualitative sense it is possible to understand some important properties of process. Let’s say that process begins with a smooth cluster which then particles join during the aggregation limited by diffusion; when the cluster is still small, some particles can stick purely casually on any one site of its surface. In other words, thanks to “noise”, i.e. existence of a random element in behavior of particles, on a surface of object tiny hillocks and poles [6,7] are formed The obtained optical and AFM images in Figures 1-10 showed long-term natural processes of aggregation, restricted diffusion leading to the formation of fractal structures on the model of Sander-Vitena [8]. This model allowed to describe evolution of a cluster and to track details of its growth, it is applicable and for the description of natural structures. The most probable consideration of superficial structures scales of fishes on model of Witten-Sander called (grating) grid is suitable for an initial stage of their growth. The subsequent growth of particles has to connect circles branching trajectories of lines and answer SSA—model (a cluster—cluster aggregation) [9]. The being formed friable clusters (strips) in certain time (year after year) connect concentric educations (threads). It is a limit case when formation of networks of channels on scales for every year comes to the end. Further, we consider those fractal formations and processes that may be analogs of surface fractal structures on scales of a fish-Kutum. If to put voltage to an electrode concerning a slice of film with a photoemulsion or a plate from an insulating material on which small powder is scattered, there will be the electric discharge leaving a trace in the form of twisting beams, in a form reminding outlines of an atmospheric lightning (see the left bottom fragment of drawing below). The form of such trace is called as “Likhtenberg’s figure”. It is about dielectric breakdown which creates luminescence structure. Being shone areas of dielectric (for example, scales of fish) after which breach current proceeds, it is similar to the fractal cluster which fractal dimension makes 1.7 [7]. On the base of the mechanism of formation of Lichtenberg shapes lies apparently aggregation limited diffusion. [7] The mechanism of formation of channels on the scales of Kutum may be similar to the mechanism of formation of Lichtenberg figures (compare with Figure 10). Within this mechanism of growth offered by Mikin [6] formation of many clusters which can move and unite in larger objects is possible. Aggregation models can appear very useful means for the description and identifications mechanism cluster nanoeducations on a surface about which testify AFM-nanoledges images (Figures 7-9). At the same time it should be noted that fractals, of course, don’t describe all objects meeting in the nature with creepingaway rarefied structure. About fractal nature of objects on a surface of living beings tells also consideration of live organisms as dissipative structures. Details of the description and the fractal characteristics are given in the figure captions.
3. Conclusion
The morphology analysis of almost all parts of a surface of fishes showed that their structure has fractal character. Fractal character is inherent in a skeleton of fishes, muscles, scales and dynamics of movement of all fishes. To estimate this fractality is easy. Almost all morphological features of the ordered superficial channels of fish-Kutum testify it. The aggregations which were formed as a result of process, limited diffusion the creeping-away rarefied fractal structures on scales fishes are similar to Likhtenberg’s figures, formed at an electric discharge and to structures of a layer of the zinc postponed at electrolysis. There are assumptions that sensitive cells of bodies of touch systems can be formed by clusters from nanoobjects of the scales. So, on the surface of the fish found complex non-Euclidean objects, images of which are natural.
REFERENCES
- B. Mandelbrot, “Fractal Geometry of the Nature,” Institute of Computer Researches, 2002, 656 p.
- E. L. Goldberger, “Bend Down of River, West B. Dzh. Chaos and Fractals in Human Physiology,” The Science World, 1990, No. 10.
- B. A. Bagatykh, “Fractal Structures Live and Evolutionary Process,” Magazine of the General Biology, Vol. 67, No. 4, 2006, pp. 243-255.
- V. Ponomarenko, “Fishery, (Russia),” No. 3, 1993, pp. 45- 46.
- A. A. Suslov and S. A. Chizhik, “Scanning Probe Microscopes (Review),” Materials, Technologies, Tools, Vol. 2, No. 3, 1997, pp. 78-79.
- M. Kolb, “Aggregation Processes, Fractals in Physics,” Works VI of the International Symposium on Fractals in Physics, July 1985, pp. 370-373.
- B. M. Smirnov, “Physics of Fractal Clusters,” Science, Moscow, 1991, p. 134.
- T. A. Witter and L. M. Sandar, Physical Review Letters, 1981, Vol. 47, 1981, p. 1400.
- J. F. Fractals, Department of Physics University of Oslo, Oslo, 1990, p. 258.

