Open Journal of Composite Materials
Vol.3 No.2A(2013), Article ID:30678,6 pages DOI:10.4236/ojcm.2013.32A002
Geometrical Modeling of Walls of Multiwall Carbon Nanotube
![]()
Department of Instrumentation and Applied Physics, Indian Institute of Science, Bangalore, India.
Email: *hembram3000@yahoo.com
Copyright © 2013 K. P. S. S. Hembram et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received March 1st, 2013; revised March 30th, 2013; accepted April 16th, 2013
Keywords: Carbon Nanotube; Concentric Walls; Diameter; Hexagons
ABSTRACT
The relationship between the adjacent walls of the multiwall carbon nanotube (MWCNT) has been investigated and geometrical formulations have been derived. We have provided the relative index for each wall, owing to the diameter of the MWCNT. The index is higher for the smaller inner diameter MWCNT, and smaller for the higher inner diameter MWCNT. In the second formulation, we have put an empirical relation between the ratio of number of hexagons in the adjacent walls of two different sub-lattices. One can speculate the properties of inner walls from these relations by obtaining the accurate diameter of the concentric walls of a MWCNT.
1. Introduction
Multiwall carbon nanotubes (MWCNTs) are concentric graphene layers, rolled with nanometer size diameter [1]. The carbon atoms are bonded by s bonds axially due to three superposed sp2 hybrid orbitals. Additionally the p bond results between adjacent layers, by van der Waals force. There are many relations among different parameters of CNT, and a pair of integers, (n,m) are the most important one, governing them. The unit basis vectors along with these integers describes most of the parameters like chiral vector, chiral angle, length and diameter of the CNT [2-4].
Depending on the nanotube chirality and diameter, a CNT can be either metallic or semiconducting. It is theoretically predicted that 1/3 of as prepared CNTs are metallic and 2/3 are semiconducting. Moreover, the band gap of the nanotube is tuned by adjusting the diameter of the nanotube. Hence electronic structure of a CNT depends only on its geometrical dimension without any doping [3]. Attempts have been made to specify the indices for a given diameter, with theoretical refinement [5]. However, it is valid for single wall CNT, and is complex for MWCNT. The diameter of concentric walls of CNT and its relation with the interlayer spacing is also investigated [6].
Aiming to understand the properties of concentric walls of MWCNT, we here derive two relations based on their diameter only. The first relation depicts the CNT wall index, owing to the ratio of diameters of two adjacent walls of the MWCNT. In the second, it relates the ratio of no. of hexagons in two adjacent walls of different sub lattices of MWCNT.
2. Experimental
There are various preparation processes like arc discharge, laser ablation, chemical vapor deposition (CVD), plasma enhance CVD, which are routinely used to synthesize CNTs [7]. In the present case we use two different experimental setup to synthesize MWCNTs.
2.1. Synthesis by Pyrolysis of Benzene in Resistive Heater
In one setup, benzene (5 ml) is pyrolised (at 750˚C) along with ferrocene (50 mg) to obtain carbon and iron species in a closed quartz tube (diameter 10 mm, length 500 mm), by the following reactions.
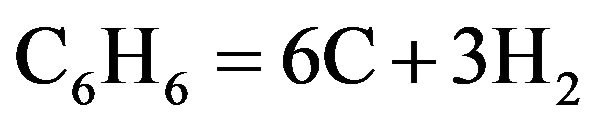 (1)
(1)
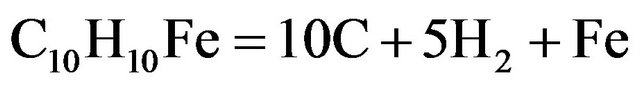 (2)
(2)
The quartz tube which is on the resistive heater, is closed at one end containing precursor and the other end is closed by a rubber bladder (see Figure 1(a)). The fresh catalytic particles formed at higher temperature, acts as
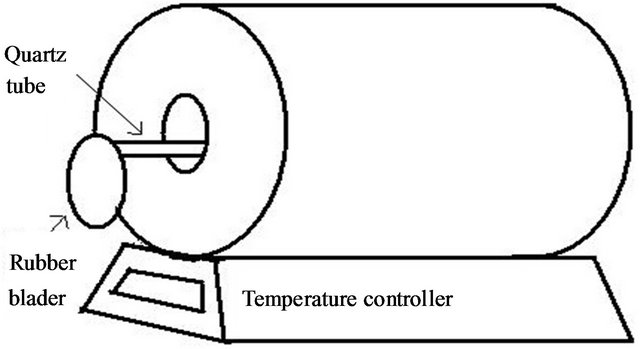 (a)
(a)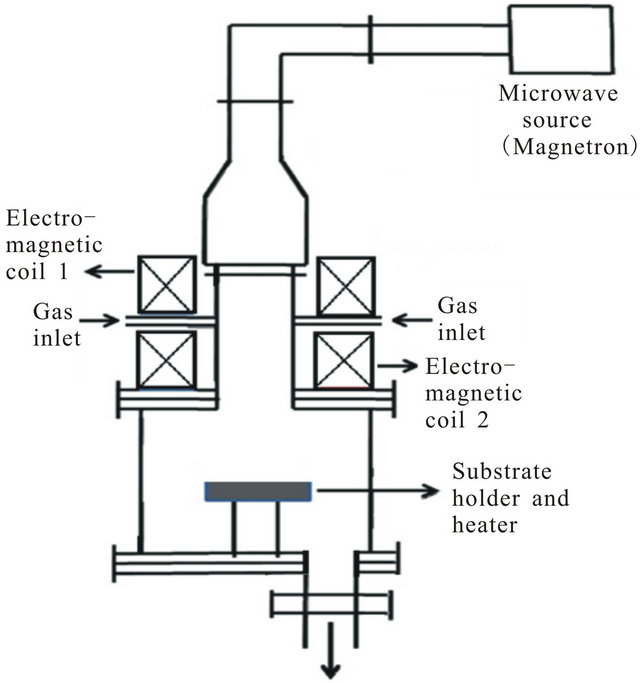 (b)
(b)
Figure 1. CNT preparation methods: (a) Resistive heater setup; and (b) ECRPECVD setup (length not to scale).
seed, and the active carbon species react with it to form CNTs (see ref. [8,9] for details). CNTs formed in this way deposit on the inner wall of the quartz tube. At room temperature the quartz tube is taken out and the bladder is removed to collect CNTs for characterization.
2.2. Synthesis by Decomposing Methane in Electron Cyclotron Resonance Plasma Enhanced Chemical Vapor Deposition (ECRPECVD)
In another setup, methane is pyrolised with ECR plasma (500 W) to obtain carbon species, in a home-built ECRPECVD chamber (see Figure 1(b)) [10], by the following reaction.
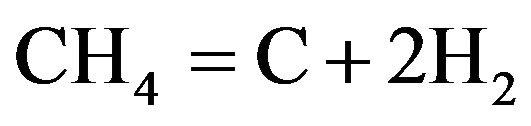 (3)
(3)
Nickel-coated Si substrates (at 500˚C) were used on which CNTS were grown. Initially, a nickel film (~40 nm) was deposited on a Si(111) substrate at room temperature by magnetron sputtering at a working pressure of 5 × 10−3 mbar (argon) while the base pressure of the system was 1 × 10−5 mbar. During CNT preparation, the working gas pressure was maintained at 6 × 10−4 mbar by using a mass-flow controller with a flow rate 10 sccm. Vertically aligned CNTs were grown with −200 V DC substrate bias. The growth time for CNTs was 30 min. The details of the preparation process has been describe elsewhere [9,11].
3. Results and Discussion
3.1. Structural Features
Field emission SEM (FEI SIRION, XL40) was used to study the morphology of the CNTs. Figure 2(a) shows the SEM image of the as grown CNTs prepared by pyrolysis of benzene in resistive heater setup. There are many CNT mats seen in the larger view, and each mat consist of many CNTs. The magnified image is seen in the Figure 2(b). The CNTs are seen to be parallel to each other with length of ~150 µm and diameter of ~10 - 80 nm. Figure 2(c) shows the SEM image of the as grown CNTs prepared by decomposing methane in ECRPECVD setup, on a Si substrate. The magnified image is shown in the Figure 2(d). The CNTs with length ~2 µm and the diameter ~50 to 150 nm are observed.
Field emission TEM (FEI TECNAI, G2 F30) was used to confirm the MWCNT. Figures 3(a) and (b) show the TEM images of the CNTs prepared by pyrolysis of benzene. It is clearly seen that the CNTs are multiwall in nature. Similarly the CNTs are multiwall in nature, which are prepared by decomposing methane in ECRPECVD setup as shown in the Figures 3(c) and (d).
Based on the observation of SEM images from both experimental setup, it is concluded that, the CNTs are grown, parallel to each other. The CNT diameters observed from both SEM and TEM images are consistent, for each experimental growth condition.
3.2. Growth Mechanism
The preparation of CNTs by pyrolysis of benzene is argued to be base growth. Figure 3(a) shows the absence of catalyst particle at the close end of a MWCNT. On the other hand the presence of the catalyst particle is clearly observed at the end of the MWCNT (see Figure 3(b)). In the later figure the catalyst particle is detached from the original catalyst particle, which is present at the base. It is confirmed by the presence of several graphene layers covering the catalyst particle supporting base growth mechanism [12,13].
The synthesis of CNTs by ECRPECVD method is considered to be tip growth. Figure 3(c) shows two MWCNT. The presence of catalyst particle at the tip in one MWCNT and its absence at the base of another CNT confirms tip growth mechanism. Similar features are seen in the Figure 3(d) also [9,11].
In the base growth, the catalyst particle is at the base,
 (a)
(a) (b)
(b) (c)
(c) (d)
(d)
Figure 2. SEM images of CNTs: (a) Prepared by pyrolysis of benzene; (b) Magnified image of (a); (c) Prepared by decomposing methane; (d) Magnified image of (c).
 (a)
(a) (b)
(b) (c)
(c) (d)
(d)
Figure 3. TEM images of CNTs: ((a) and (b)) Prepared by pyrolysis of benzene; ((c) and (d)) Prepared by decomposing methane.
through which carbon atom diffuses from the bottom of the catalyst to the top side where the nucleation of the CNTs happens. The diffused carbon atom joins with the CNTs, pushing it forward (see Figure 4(a)). In the tip growth the catalyst particle is at the tip, where the active carbon atom comes in contact with the catalyst particle and, it diffuses from the top to the bottom side pushing the CNT backward (see Figure 4(b)). The most common feature from both the cases is the decomposition of hydrocarbon on the metal surface and diffusion through it. Hence the vapor-liquid-solid (VLS) mechanism prevails in most of the cases and is verified with many different experimental setup [14,15]. In our both the cases, we also support VLS mechanism owing to both base growth and tip growth. The details of the mechanism is described elsewhere [16,17].
3.3. The Formalism
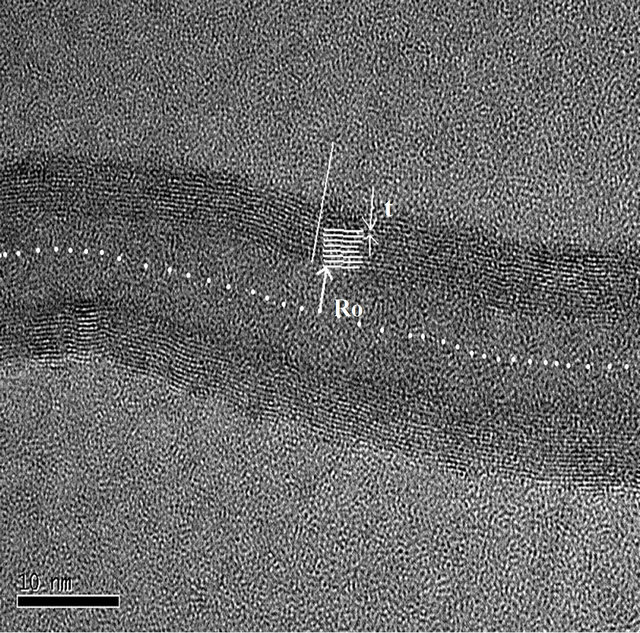
Formulation 1: MWCNT can be modeled as concentric cylinders (see Figure 5). We deduce the formulas based on the HRTEM images of MWCNT, obtained from the pyrolysis of benzene (see Figures 6(a) and (b)). Taking the ratio of two adjacent walls of MWCNT, we obtain the index of the outer wall as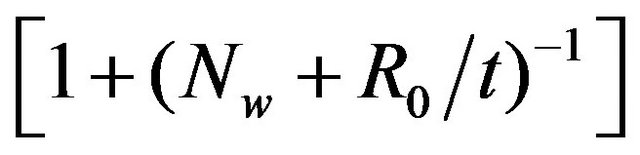 , where
, where

Figure 4. Growth mechanism, describing base and tip growth of MWCNT.
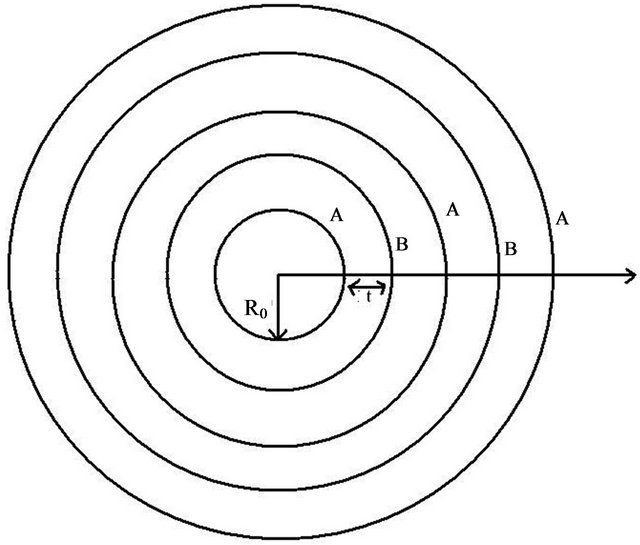
Figure 5. Schematic diagram mimicking a MWCNT showing “A” and “B” sublattices.
(a)

(b)
Figure 6. Modeling of a MWCNT (R0 is the inner radius and t is the inter wall thickness).
“Nw” is the Nth no. of nanotubes from the center, “R0” is the inner radius of the MWCNT and “t” is the average interlayer separation of the MWCNT. Plotting the wall index versus the no. of walls, we obtain the graph as shown in the Figure 7. Higher value of the wall index, indicates that the inner diameter of the MWCNT is less. And the smaller wall index indicates the higher diameter of the MWCNT.
Formulation 2: The no. of hexagons, Nh per unit cell of a chiral nanotube, is given by

Figure 7. CNT wall index as a function of no. of walls in the MWCNT.
where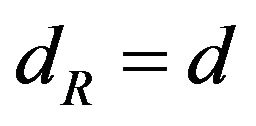 , if
, if 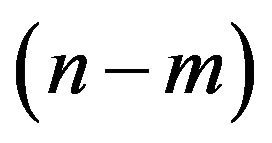 is not a multiple of 3d, or
is not a multiple of 3d, or , if
, if 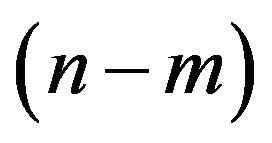 is a multiple of 3d, where d is defined as the largest common divisor of
is a multiple of 3d, where d is defined as the largest common divisor of  [4].
[4].
Let there be a certain no. of unit cells be present in the unit length of the MWCNT. Taking the ratio between the different stacking in CNTs, we obtain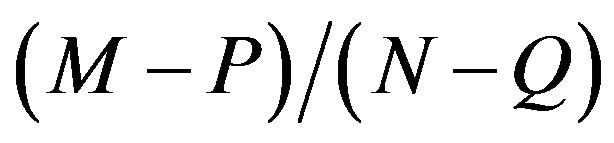 , where M, N are the no. of unit cells in the sub-lattice A and B respectively. P and Q are the excess no. of unit cells in the unit length of the penultimate sub-lattice of A and B respectively. If the excess no. of unit cell in the inner side wall of the A and B sub-lattice of the can be represented as
, where M, N are the no. of unit cells in the sub-lattice A and B respectively. P and Q are the excess no. of unit cells in the unit length of the penultimate sub-lattice of A and B respectively. If the excess no. of unit cell in the inner side wall of the A and B sub-lattice of the can be represented as , and
, and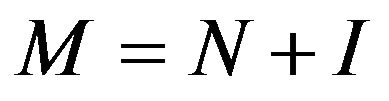 , then we obtain
, then we obtain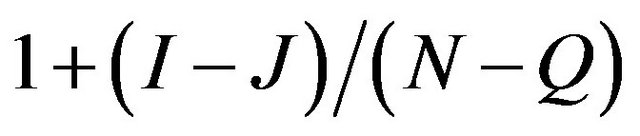 . Hence the ratio of no of hexagons in the adjacent walls is
. Hence the ratio of no of hexagons in the adjacent walls is
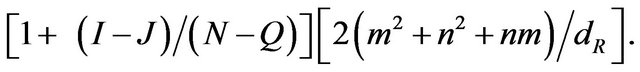 (4)
(4)
Directly taking the ratio of no of hexagons, in the different sub-lattice of MWCNT, one can obtain
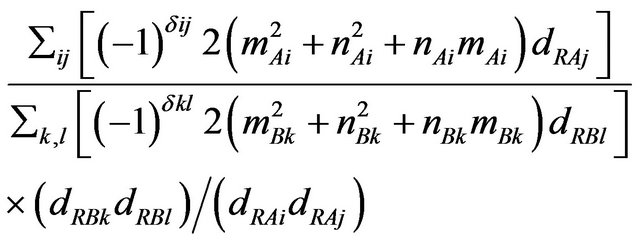 (5)
(5)
In the reality both the Equations (3) and (4) represent the same quantity. Hence putting them equal we obtain
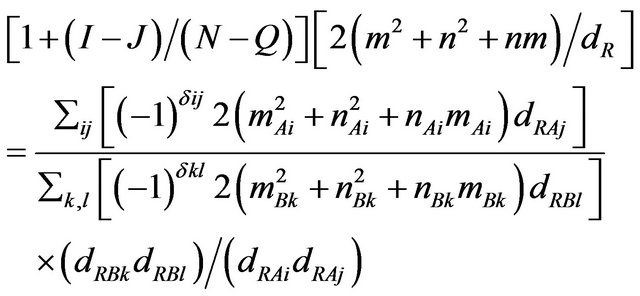 (6)
(6)
The pair of integers 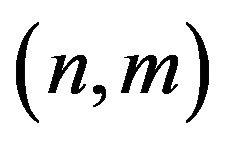 are the two independent parameters of a particular wall of the nanotube. The no. of hexagons in a finite length nanotube is also fixed, for a certain diameter. But the increase in no. of hexagons, moving radially outward of a particular MWCNT, provides the value of P, Q, I and J. In future, (we expect with the development of sophisticated TEM), with careful measurements, one can obtain the accurate value of the diameter nanotube. Hence for a unit length the value of n and m can be predicted. Obtaining the value of n and m, one can estimate the value of no. of unit cells in the sub lattices (i.e. the values of M, N, P, Q, I, J can be calculates), and hence the no. of hexagon in a particular wall.
are the two independent parameters of a particular wall of the nanotube. The no. of hexagons in a finite length nanotube is also fixed, for a certain diameter. But the increase in no. of hexagons, moving radially outward of a particular MWCNT, provides the value of P, Q, I and J. In future, (we expect with the development of sophisticated TEM), with careful measurements, one can obtain the accurate value of the diameter nanotube. Hence for a unit length the value of n and m can be predicted. Obtaining the value of n and m, one can estimate the value of no. of unit cells in the sub lattices (i.e. the values of M, N, P, Q, I, J can be calculates), and hence the no. of hexagon in a particular wall.
3.4. Discussion
The inner diameter of MWCNT is mainly governed by the size of the catalyst particle, and is treated as independent parameter for this modeling. Again in this process, we take the average distance between the adjacent walls of the CNT. However the inter wall spacing can actually range from 0.34 to 0.39 nm, and the inter wall spacing increases with decreasing CNT diameter, and this effect is more pronounced in small diameter nanotubes due to high curvature [6,18]. The interlayer separation is related to the diameter of the CNT with the following relation
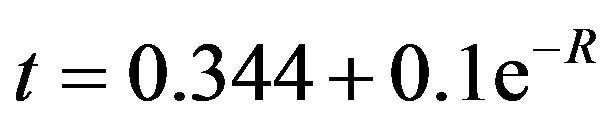 (7)
(7)
where R is the inner radius of the CNT [6]. Hence exact calculation of the wall index of CNT, is cumbersome, but is predictable. As it depends only on the diameter of the wall, (not on its length). Although at present, it is difficult to isolate the single walls from a MWCNT, its individual properties is difficult to predict. In our attempt from Equation (6), one can predict their properties, obtaining only the diameter.
However factors like Peierls distortion [2] also affects the properties of inner wall, and can’t be ruled out. Experimental evidences, with the presence of pentagons/ heptagons at the bent portions of CNT, the spacing between layers increases up to 0.41 nm [19]. With strict “ABAB” stacking, it is very difficult to form curved surface. Turbo static stacking allows the concentric wall to slide, hence easier to bend and twist [20]. So the walls of the MWCNT compromise stacking between “turbo static” to “ABAB”. Hence the properties of hexagons of different walls are different from each other. Owing to Equation (6) the no. of hexagons is not affected by stacking. The limiting point of this relation may be due to factors like presence of 1) non-hexagonal rings, and 2) dangling bonds. Attempts have been made to count the no. of hexagons based on structural imaging through HRTEM. Moving towards the adjacent outer wall, the increases in average excess hexagon is ~9.6. Low helicity of the tube affects little change, while quantifying no. of hexagons and can’t be ruled out fully [21]. With more experimental support, we intend to justify our proposal in future. Hence in this attempt, we only provide the quantitative measure of hexagons, based on a geometrical parameters, as the qualitative nature too complex to explored. Our formulations fail for single wall CNT.
4. Conclusion
In summary, we elucidate two relations between the walls of the MWCNT. In the first relation we have proposed wall index for CNT, based on the ratio of the radius of the concentric walls. The index is higher for the smaller inner diameter MWCNT and smaller for the higher inner diameter MWCNT. In the second formulation, we have put an empirical relation between the ratio of no. of hexagons in the adjacent two different sub lattices. We expect the nature of inner walls can be predicted by calculating the no. of unit cells in the sub lattices that can be obtained from the accurate diameter of the concentric walls of a MWCNT.
5. Acknowledgements
We are thankful to nano-centre, Indian Institute of Science for providing the facilities for characterizing the samples.
REFERENCES
- S. Iijima, “Helical Microtubules of Graphitic Carbon,” Nature, Vol. 354, 1991, pp. 56-58. doi:10.1038/354056a0
- M. S. Dresselhaus, G. Dresselhaus and R. Saito, “Carbon Fibers Based on C60 and Their Symmetry,” Physical Review B, Vol. 45, No. 11, 1992, pp. 6234-6242. doi:10.1103/PhysRevB.45.6234
- R. Saito, M. Fujita, G. Dresselhaus and M. S. Dresselhaus, “Electronic Structure of Chiral Graphene Tubules,” Applied Physics Letters, Vol. 60, No. 18, 1992, pp. 2204- 2206. doi:10.1063/1.107080
- M. S. Dresselhaus, G. Dresselhaus and R. Saito, “Physics of Carbon Nanotubes,” Carbon, Vol. 33, No. 7, 1995, pp. 883-891. doi:10.1016/0008-6223(95)00017-8
- L. Chkhartishvili and T. Berberashvili, “Geometrical Model Based Refinements in Nanotube Chiral Indices,” World Journal of Nano Science and Engineering, Vol. 1, No. 2, 2011, pp. 45-50. doi:10.4236/wjnse.2011.12007
- C. H. Kiang, M. Endo, P. M. Ajayan, G. Dresselhaus and M. S. Dresselhaus, “Size Effects in Carbon Nanotubes,” Physical Review Letters, Vol. 81, No. 9, 1998, pp. 1869- 1872. doi:10.1103/PhysRevLett.81.1869
- R. Saito, G. Dresselhaus and M. S. Dresselhaus, “Physical Properties of Carbon Nanotubes,” World Scientific, Singapore, 1998.
- K. P. S. S. Hembram and G. Mohan Rao, “Structural and Surface Features of Multiwall Carbon Nanotube,” Applied Surface Science, Vol. 257, No. 13, 2011, pp. 5503- 5507. doi:10.1016/j.apsusc.2010.12.132
- K. P. S. S. Hembram, K. Reddappa Reddy and G. Mohan Rao, “Determination of Growth Direction of Carbon Nanotubes from the Shape of the Catalyst Particle,” International Journal of Nanoscience, Vol. 10, No. 4-5, 2011, pp. 1045-1050. doi:10.1142/S0219581X11008575
- K. D. Vargheese and G. Mohan Rao, “Electron Cyclotron Resonance Plasma Source for ion Assisted Deposition of Thin Films,” Review of Scientific Instruments, Vol. 71, No. 2, 2000, pp. 467-472. doi:10.1063/1.1150225
- S. K. Patra and G. Mohan Rao, “Field Emission Current Saturation of Aligned Carbon Nanotube—Effect of Density and Aspect Ratio,” Journal of Applied Physics, Vol. 100, No. 2, 2006, Article ID: 024319. doi:10.1063/1.2219082
- S. Fan, M. G. Chapline, N. R. Franklin, T. W. Tombler, A. M. Cassell and H. Dai, “Self-Oriented Regular Arrays of Carbon Nanotubes and Their Field Emission Properties,” Science, Vol. 283, No. 5401, 1999, pp. 512-514. doi:10.1126/science.283.5401.512
- D. H. Kim, H. S. Jang, C. D. Kim, D. S. Cho, H. S. Yang, H. D. Kang, B. K. Min and H. R. Lee, “Dynamic Growth Rate Behavior of a Carbon Nanotube Forest Characterized by in Situ Optical Growth Monitoring,” Nano Letters, Vol. 3, No. 6, 2003, pp. 863-865. doi:10.1021/nl034212g
- M. M. Shaijumon, A. L. M. Reddy and S. Ramaprabhu, “Single Step Process for the Synthesis of Carbon Nanotubes and Metal/Alloy-Filled Multiwalled Carbon Nanotubes,” Nanoscale Research Letters, Vol. 2, 2007, pp. 75- 80. doi:10.1007/s11671-006-9033-5
- R. K. Sahoo, V. Daramalla and C. Jacob, “Multiwall and Bamboo-Like Carbon Nanotube Growth by CVD Using a Semimetal as a Catalyst,” Materials Science and Engineering: B, Vol. 177, No. 1, 2012, pp. 79-85. doi:10.1016/j.mseb.2011.09.003
- K. P. S. S. Hembram and G. Mohan Rao, “Origin of Structural Defects in Multiwall Carbon Nanotube,” Materials Letters, Vol. 72, 2012, pp. 68-70. doi:10.1016/j.matlet.2011.12.078
- R. T. K. Baker, “Catalytic Growth of Carbon Filaments,” Carbon, Vol. 27, No. 3, 1989, pp. 315-323. doi:10.1016/0008-6223(89)90062-6
- M. Endo, K. Takeuchi, T. Hiraoka, T. Furuta, T. Kasai, X. Sun, C. H. Kiang and M. S. Dresselhaus, “Stacking Nature of Graphene Layers in Carbon Nanotube and Nanofibers”, Journal of Physics and Chemistry of Solids, Vol. 58, No. 11, 1997, pp. 1707-1712. doi:10.1016/S0022-3697(97)00055-3
- M. Liu and J. M. Cowley, “Structures of Carbon Nanotubes Studied by HRTEM and Nanodiffraction,” Ultramicroscopy, Vol. 53, No. 4, 1994, pp. 333-342. doi:10.1016/0304-3991(94)90046-9
- X. Sun, C. H. Kiang, M. Endo, K. Takeuchi, T. Furuta and M. S. Dresselhaus, “Stacking Characteristics of Graphene Shells in Carbon Nanotubes,” Physical Review B, Vol. 54, No. 18, 1996, pp. R12629-R12632. doi:10.1103/PhysRevB.54.R12629
- M. Bretz, B. G. Demczyk and L. Zhang, “Structural Imaging of a Thick Walled Carbon Nanotube,” Journal of Crystal Growth, Vol. 141, No. 1-2, 1994, pp. 304-309. doi:10.1016/0022-0248(94)90124-4
NOTES
*Corresponding author.

