Journal of Power and Energy Engineering
Vol.05 No.10(2017), Article ID:79981,15 pages
10.4236/jpee.2017.510002
Electrical Power Losses in a Photovoltaic Solar Cell Operating under Partial Shading Conditions
Abdouramani Dadjé1,2, Noël Djongyang1, Réné Tchinda3
1Department of Renewable Energy, National Advanced Polytechnic School, University of Maroua, Maroua, Cameroon
2School of Geology and Mining Engineering, University of Ngaoundéré, Ngaoundéré, Cameroon
3LISIE, Fotso Victor University Institute of Technology, University of Dschang, Dschang, Cameroon

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: September 18, 2017; Accepted: October 27, 2017; Published: October 30, 2017
ABSTRACT
The aim of this paper is to determine the power losses recorded by a PV generator operating under partial shading conditions. These losses are evaluated through two distinct methods. The first method is based on mathematical modeling, while the second is based on Simulink’s physical model. The losses recorded are considerable and increase as a function of the increase in the percentage of shading up to a limit value where they become constant in the case where an ideal by-pass diode is connected in parallel with the modules. This limit value is non-existent in the case where the bypass diode is not ideal, which in fact corresponds to the real model. However, it emerges that the power losses are minimized in a PV system comprising bypass diodes, in particular in the case where the partial shading is considerable.
Keywords:
Electrical Power Losses, PV Generator, Partial Shading Conditions, Mathematical Modeling, Simulink’s Physical Model

1. Introduction
Photovoltaic solar cell is a generator able to produce electrical energy when subjected to solar radiation. The characteristics of the photovoltaic generator or module (such as current or voltage) given by the manufacturer are determined under the so-called standard test conditions (Tc = 25˚C, G = 1 kW/m², AM = 1.5). However, in practice several factors can influence these data and negatively impact the electric power produced by the solar generator. Among these factors it is the phenomenon of partial shading which can not only reduce the power of the generator but also can decrease its lifespan due to the hot spot. Among the causes inducing partial shading it is the trees, the clouds, the constructions near that are installed in the photovoltaic generators [1] .
There are several configurations of a photovoltaic solar field. In order to meet the electricity requirement in any application, the solar modules are arranged in series, in parallel, in bridged and in full cross connections to form a photovoltaic array to match the power requirements in terms of voltage and current [2] . When the photovoltaic field is subjected to the phenomenon of partial shading, an uneven distribution of solar radiation is observed on the surface of the field. This situation gives rise to several maxima in the power-voltage characteristic of the PV generator [3] . Furthermore, the effect of shade on the output power of a typical PV system is nonlinear, because a small amount of shade on a part of an array can cause a large reduction in output power [2] . In this case, it becomes very complex to determine the maximum power of a PV generator under partial shading conditions. Solutions to this problem are usually found using a system of control of the maximum power delivered by the solar generator [4] . This control system makes it possible to fix the maximum point by thus improving the power at the output of the generator.
Several theoretical studies have been carried out in order to determine the maximum power produced by a PV generator subjected to the partial shading conditions, thus permitting to evaluate the losses generated by this phenomenon. The determination of the maximum power requests to determine the parameters of the module. The number of these parameters varies according to the solar cell model studied. One distinguishes the photovoltaic solar cell model with one diode (with five parameters) and the photovoltaic solar cell model with two diodes (with seven parameters) [3] - [8] . Generally, in the determination of the parameters of a solar module, it requires to make certain approximations because few equations are available for several parameters to be determined. Moreover, the characteristic equation of the PV generator is a non-linear equation, which makes it more complex to solve the problem.
The aim of this paper is to evaluate the power losses generated by the phenomenon of partial shading in a PV generator. The study is based on the one diode electrical model of the PV solar cell. The mathematical methods used are analytic and iterative. The solar module (made up of several cells) is subdivided into two subgroups or submodules with an equal number of cells. A diode by pass is connected in parallel to each subgroup of the module in order to dampen the influence of partial shading [5] [6] [7] [8] . The implementation of the results is done under the MATLAB Simulink environment. This implementation is applied to three different types of photovoltaic technologies: CIS thin film, Monocrystalline and Polycrystalline.
2. Mathematical Modeling Method
2.1. Parameters Determination
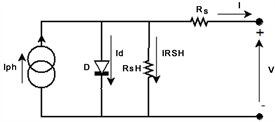
This part is devoted to the determination of the parameters of the PV generator subjected to partial shading conditions. The electrical equivalent circuit of a one diode photovoltaic solar cell is presented in Figure 1. The five parameters of this model include Iph, Io, n, Rs and Rsh.
Applying Kirchhoff’s law to this model permits to obtain the characteristic equation current-voltage of the solar cell defined by [1] [9] [10] :
(1)
Considering the fact that Rsh>>>, thus . Equation (1) turns to [1] [9] [10] :
(2)
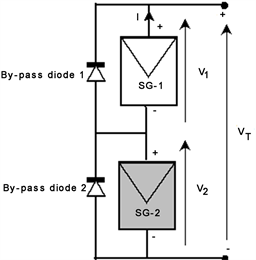
The configuration of the PV module subjected to partial shading conditions is presented in Figure 2. The module is subdivided into two subgroups of 18 cells each. One of the subgroups is not shaded (called SG-1 with Ns1 number of cells) while the other is subjected to partial shading (called SG-2 with Ns2 number of cells).
The total voltage across the module is given by:
(3)
where:
(4)
(5)
Equation (6) gives the photovoltaic current as [9] [11] :
(6)
The saturation current is evaluated through Equation (7) [9] [10] :
(7)
For I = 0, V = Voc, Iph = Isc, thus Equation (1) turns to:
(8)
Then:
(9)
Figure 1. Circuit equivalent to single-diode for a photovoltaic cell.
Figure 2. Configuration of the PV module subdivided into two subgroups of 18 cells each.
Replacing Equation (9) into Equation (7) permits to define the value of the saturation current as:
(10)
At the maximum power point (where I = Imp and V = Vmp), one has:
(11)
In Equation (9) and Equation (11), the exponential term is much greater than the first term (by considering the fact that the value of the reverse saturation current for any diode is in the order of 10−5 and 10−6 A [9] ). Thus by assuming that Iph,ref ≈ Isc, Equation (9) and Equation (11) turn to:
(12)
(13)
Combining Equation (12) and Equation (13) leads to:
(14)
From Equation (2), one gets the partial derivative of V with respect to I as:
(15)
Equation (2) permits to deduce the series resistance at the open circuit point such as:
(16)
One approximates the value of the derivative of V with respect to I by fixing two points (Voc, 0) and (Vmp, Imp) such as:
(17)
Replacing Equation (12) and Equation (17) into Equation (16) permits to get the series resistance of each solar cell as:
(18)
Replacing Equation (18) into Equation (14) leads to:
(19)
The value of the parameter Rsh is calculated by solving the Equation using Newton Raphson method (iterative method).
2.2. Determination of Peak Power Parameters
The power of the PV module is given as follows:
(20)
Using the power-voltage characteristics at the maximum power point implies:
(21)
where
(22)
From Equation (2), the partial derivative of I with respect to V is:
(23)
Let us set
(24)
Replacing Equation (23) and Equation (24) into Equation (22) leads to:
(25)
Equation (25) is solved by the Newton Raphson method.
Principe of Newton-Raphson Method
The Newton-Raphson method finds the tangent line of the function at the current point and uses the zero of tangent line as the next reference point. The process is repeated until the root is found. The function can be expanded in the neighborhood of the root through the Taylor formula:
where x can be seen as a trial value for the root. At the nth step of the approximate value of the next step; can be derived from:
is called the Newton-Raphson method.
The flowchart of Figure 3 details the method of resolution of Newton Rapson.
Combining Equation (3), Equation (4) and Equation (5) leads to the total maximum voltage of the PV module given by:
(26)
Figure 3. Flowchart of Newton-Raphson method.
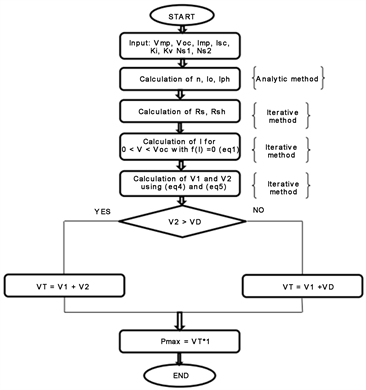
Figure 4 presents the Flowchart describing the process for determining the maximum power of a PV module under partial shading conditions based on mathematical modeling.
3. Simulink Model of the PV Generator
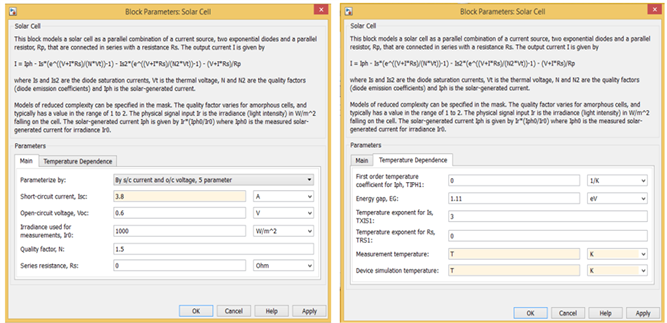
The Simulink models of the used panels are designed from the solar cell of Simulink Library of Matlab. By double-clicking the component of the Figure 5, the window of the Figure 6 opens the essential parameters such as saturation current Isc are modified in accordance to the manufacturer’s datasheet of the PV panel to simulate. As for the temperature, it is preferable to insert the letter T in the relevant field to facilitate change during the simulations. The irradiance (Ir) is simulated from the constant block (Figure 7) which must be connected to the Ir inputs of the interconnected PV cells. The irradiance inputs of the solar cells of the unshaded subgroup are connected to the constant block, so the value is set to G as in Figure 8, whereas for the shaded subgroup they are connected to G* beta where “beta” is the shading coefficient ranging from 0 to 1. The choice of modules to 36 cells for this study allows keeping the same configuration for all the three panels’ technologies used.
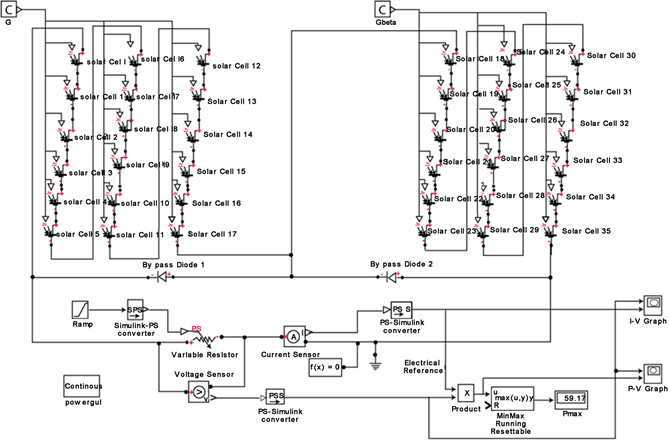
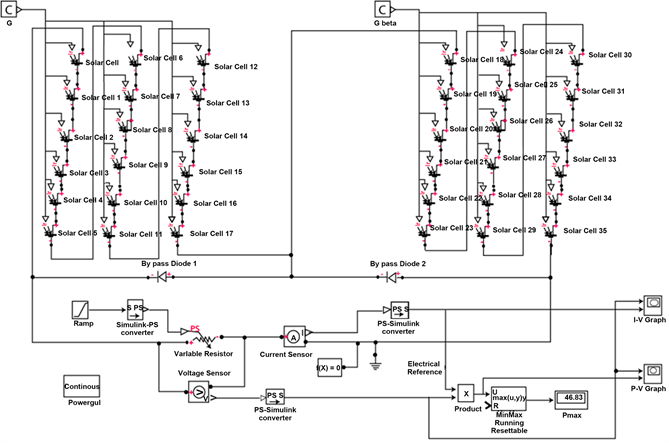
Figure 9 and Figure 10 present the Simulink model of a PV module respectively without shading and with partial shading. The simulation example has been done for MSX-60 multicrystalline module.
4. Results and Discussion
The simulation results are based on the flow chart presented in Figure 4 and on the manufacturer data presented in Table 1 for each solar technologies used. The aim is to extract the maximum power output of the PV module and evaluate the losses. Both analytical and Simulink model are used.
Figure 4. Flowchart describing the process for determining the maximum power of a PV module under partial shading conditions based on mathematical modeling.
Figure 5. Simulink model of solar cell.
Figure 6. Configuration of solar cell parameters.
Figure 7. PS Constant block of Simulink /Matlab.
Figure 8. Configuration of PS constant block parameters.
Figure 9. Simulink PV module model without shading (β = 1).
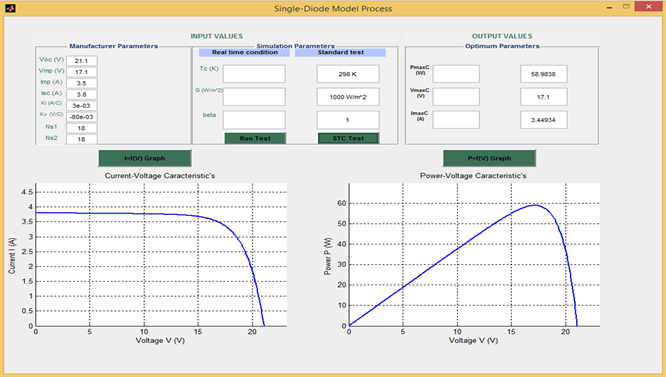
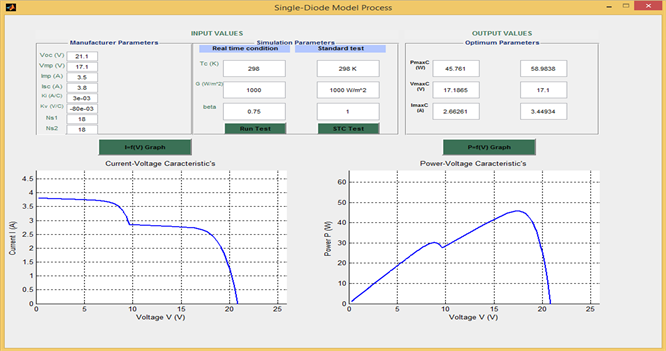
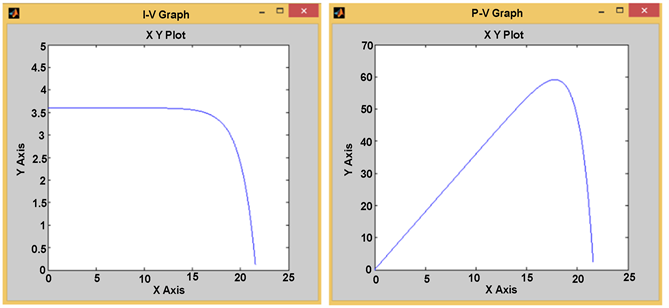
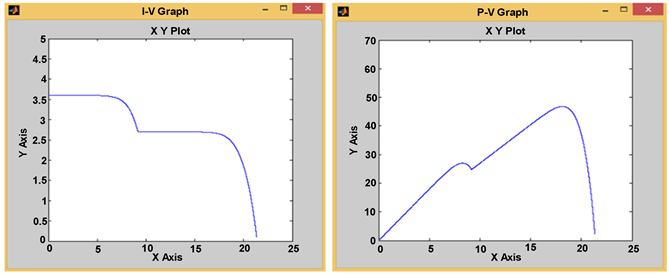
Figure 11 and Figure 12 present the I-V and P-V characteristics of the PV generator respectively without shading and with shading, simulated in MATLAB based on the parameters determined analytically in Section 2. Figure 13 and Figure 14 present the I-V and P-V characteristics of the PV generator based on Simulink model respectively without shading and with shading.
Figure 10. Simulink PV module model with partial shading (case of β = 0.75).
Table 1. Manufacturer data for different solar cell technologies at STC (25˚C, 1.5 AM, 1000 W/m2) [12] [13] [14] .
Table 1 presents the maximum power of different PV solar cell technologies including the manufacturer data, the maximum power based on analytical method calculation and the maximum power obtained through Simulink model. Different percentages of partial shading of the generator have been considered including 0% (for β = 1), 25% (for β = 0.75), 50% (for β = 0.5), 75% (for β = 0.25) and 100% (for β = 0). The losses are evaluated by differentiating between
Figure 11. I-V and P-V characteristics of a PV module without partial shading at Standard test conditions (G = 1000 W/m²; T = 25˚C; β = 1).
Figure 12. I-V and P-V characteristics of a PV module with partial shading at standard test conditions (G = 1000W/m²; T= 25˚C), β = 0.75.
the calculated power in the non-shading conditions and that calculated under the shading conditions.
Figure 13. I-V and P-V characteristics of a PV module without partial shading at Standard test conditions (G = 1000W/m²; T= 25˚C) based on Simulink model.
Figure 14. I-V and P-V characteristics of a PV module with partial shading at Standard test conditions (G = 1000 W/m²; T = 25˚C), β = 0.75 based on Simulink model.
For Monocrystalline, the relative error between the calculated maximum power (under non shading conditions) and that of the constructor is respectively 0.86142% (with the model combining the analytical and iterative methods), and 0.37142% (with the Simulink model). For Polycrystalline, the relative error between the calculated maximum power (under non shading conditions) and that of the manufacturer is respectively 1.69366% (with the model combining the analytical and iterative methods), 1.383333% (with the Simulink model). For the CIS, the relative error between the calculated maximum power (under non shading conditions) and that of the manufacturer is respectively 0.912% (with the model combining the analytical and iterative methods), 1.525% (with the Simulink model). These results permit to validate the reliability of the studied models.
The electrical power losses evaluated with the mathematical modeling method are in the range of 22.2% to 23.74% in the case of partial shading of 25%, depending on the type of photovoltaic technology. These losses are of the order of 21% to 26.2% using the Simulink model. In the case of partial shading at 50%, the losses are in the range of 48.3% to 49.6% with the mathematical method and in the range of 46.9% to 55.6% with the Simulink model.
In the case of partial shading at 75%, losses are in the range of 49.26% to 49.9% with the mathematical method and in the range of 56.5% to 58.3% with the Simulink model.
In the case of partial shading at 100%, the loss range is the same as in the case of partial shading at 75% with the mathematical method (from 49.26% to 49.9%). With the Simulink model, the losses vary from 57.5% to 60% depending on the type of PV module.
When losses approximate the value of 50%, the voltage across the shaded sub-group’s module becomes less than the voltage of the by-pass diode (0.6 V). Therefore, the by-pass diode becomes conductive and blocks the degradation of the power produced by the entire photovoltaic module. In the case of the mathematical model, it can be seen in Table 2 that the power losses are constant as a function of the percentage of shading when the by-pass diode becomes conductive (power losses are constant with the mathematical model from a percentage of partial shading of 75%). Referring to the diagram in Figure 15, it appears that the Simulink model gives losses much higher than the mathematical model for high shading percentages (from 75% partial shading). These two observations
Table 2. Maximum power losses of the PV module based on mathematical modeling and Simulink model for different PV solar cell technologies at standard test conditions.
Figure 15. Comparison between maximum power losses based on mathematical modeling and on Simulink model for different types of PV module.
would be justified by the voltage drop at the terminals of the internal resistance of the by-pass diode in the case of the Simulink model. This voltage drop is a function of the direct current when the diode is conductive and contributes negatively to the power produced by the photovoltaic solar module. Indeed, the internal resistance is considered to be zero in the case of mathematical modeling. An ideal by-pass diode with a zero internal resistance would lead to the same conclusions for both mathematical and Simulink models concerning the role of the by-pass diode connected in parallel with a shaded PV module. The by-pass diode when it is conductive would limit the losses of power (losses become constant) due to partial shading.
The analysis of these results leads to the following conclusions: 1) The influence of partial shading on the electrical energy produced by a PV generator is considerable; 2) The variation of the energy losses calculated according to the type of PV module is lower with the mathematical model compared to the Simulink model; 3) A by-pass diode connected in parallel with the shaded part of a PV module would limit the power losses to a constant threshold value, i.e. a value that will no longer vary with the increase of the percentage of shading.
The Simulink model takes into account certain parameters (such as the internal resistance of the bypass diode) which negatively influence the power produced by the PV module. These parameters are neglected in the mathematical model. The power losses evaluated with the Simulink model would therefore be closer to actual losses than those evaluated with the mathematical model.
5. Conclusion
The objective of this article was to evaluate the electrical energy losses of a PV generator subjected to partial shading conditions. Two methods were used for this purpose: the mathematical method and the method based on the Simulink model. It emerges that the energy losses recorded by a PV generator subjected to partial shading conditions are considerable. Both mathematical and Simulink models are effective method for estimating these losses. However the Simulink model is more close to the real model because it takes into account certain parameters which are ignored in the mathematical model and which nevertheless negatively influence the power produced by the PV module.
Cite this paper
Dadjé, A., Djongyang, N. and Tchinda, R. (2017) Electrical Power Losses in a Photovoltaic Solar Cell Operating under Partial Shading Conditions. Journal of Power and Energy Engineering, 5, 19-33. https://doi.org/10.4236/jpee.2017.510002
References
- 1. Prasanth Ram, J. and Rajasekar, N. (2016) A New Global Maximum Power Point Tracking Technique for Solar Photovoltaic (PV) System under Partial Shading Conditions (PSC). Elsevier, Amsterdam.
- 2. Alsayid, B.A., Alsadi, S.Y., Jallad, J.S. and Dradi, M.H. (2013) Partial Shading of PV System Simulation with Experimental Results. Smart Grid and Renewable Energy, 4, 429-435. https://doi.org/10.4236/sgre.2013.46049
- 3. Dadjé, A., Djongyang, N., Kana, J.D. and Tchinda, R. (2016) Maximum Power Point Tracking Methods for Photovoltaic Systems Operating under Partially Shaded or Rapidly Variable Insolation Conditions: A Review Paper. International Journal of Sustainable Engineering, 9, 1-16. https://doi.org/10.1080/19397038.2016.1149525
- 4. Sandrolini, L., Artioli, M. and Reggiani, U. (2009) Numerical Method for the Extraction of Photovoltaic Module Double-Diode Model Parameters through Cluster Analysis. Elsevier, Amsterdam.
- 5. Srinivasa V., Priyanka, S. and Mohammed, N. (2012) Modeling Impact of Bypass Diodes on Photovoltaic Cell Performance under Partial Shading. 2012 IEEE International Conference on Electro/Information Technology, Indianapolis, 6-8 May 2012.
- 6. Alsayid, B. (2012) Modeling and Simulation of Photovoltaic Cell/Module/Array with Two-Diode Model. International Journal of Computer Technology and Electronics Engineering, 1, 6-11. http://www.ijctee.org/files/VOLUME2ISSUE3/IJCTEE_0612_02.pdf
- 7. Nahla, M.A.A.S., Yahaya, N.Z. and Balbir, S. (2013) Single-Diode Model and Two-Diode Model of PV Modules: A Comparison. 2013 IEEE International Conference on Control System, Computing and Engineering, Penang, 29 November-1 December 2013.
- 8. Silvestre, S., Boronat, A. and Chouder. A. (2009) Study of Bypass Diodes Configuration on PV Modules. Elsevier, Amsterdam.
- 9. Ahmed, N.A. and Miyatake, M. (2008) A Novel Maximum Power Point Tracking for Photovoltaic Applications under Partially Shaded Insolation Conditions. Electric Power Systems Research, 78, 777-784. https://doi.org/10.1016/j.epsr.2007.05.026
- 10. Kouchaki, A., Iman-Eini, H. and Asaei, B. (2013) A New Maximum Power Point Tracking Strategy for PV Arrays under Uniform and Non-Uniform Insolation Conditions. Solar Energy, 91, 221-232. https://doi.org/10.1016/j.epsr.2007.05.026
- 11. Shaiek, M. Smida, B., Sakly, A. and Mimouni, M.F. (2013) Comparison between Conventional Methods and GA Approach for Maximum Power Point Tracking of Shaded Solar PV Generators. Solar Energy, 90, 107-122. https://doi.org/10.1016/j.epsr.2007.05.026
- 12. http://solargis.com/assets/graphic/free-map/DNI/Solargis-Cameroon-DNI-solar-resource-map-en.png
- 13. https://www.solarelectricsupply.com/media/custom/upload/Solarex-MSX64.pdf
- 14. http://www.solenerg.com.br/files/SP70.pdf