Journal of Power and Energy Engineering
Vol.05 No.05(2017), Article ID:76476,14 pages
10.4236/jpee.2017.55002
Performance Investigation of Three Combined Airfoils Bladed Small Scale Horizontal Axis wind Turbine by BEM and CFD Analysis
Mehedi Hasan1, Adel El-Shahat1, Musfequr Rahman2
1Department of Electrical Engineering, Georgia Southern University, Statesboro, GA, USA
2Department of Mechanical Engineering, Georgia Southern University, Statesboro, GA, USA
Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: February 18, 2017; Accepted: May 23, 2017; Published: May 26, 2017
ABSTRACT
The present work is based on the comparative study between “Blade-Element- Momentum” (BEM) analysis and “Computational-Fluid-Dynamics” (CFD) analysis of small-scale horizontal axis wind turbine blade. In this study, the pitch is considered as fixed and rotor speed is variable. Firstly, the aerodynamic characteristics of three different specialized airfoils were analyzed to get optimum design parameters of wind turbine blade. Then BEM was performed with the application of the open source wind turbine design and performance computation software Q-Blade v0.6. After that, CFD simulation was done by Ansys CFX software. Here, k-ω “Shear-Stress-Transport” (SST) model was conducted for three-dimensional visualization of turbine performance. However, the best coefficient of performance was observed at 6˚ angle of attack. At this angle of attack, in the case of BEM, the highest coefficient of performance was 0.47 whereby CFD analysis, it was 0.43. Both studies showed good performance prediction which was a positive step to accelerate the continuous revolution in wind energy sector.
Keywords:
Wind Turbine, Small Scale, Blade Design, Coefficient of Performance, BEM, CFD

1. Introduction
Strenuous exploration is continuously offered for the advancement of wind tur- bine technology. As the part of this revolution, investigation of wind turbine performance related to the aerodynamic characteristics has a significant impact on wind energy sector. Among all the wind technologies, horizontal axis wind turbine is the most efficient and popular one. However, for horizontal axis wind turbine system, performance mainly depends on blade shape and working principle. For lift-type wind turbine blade, the cross-section is made by the airfoil. The airfoil is responsible for creating aerodynamic lift force effect by making pressure difference of air flow between upper and lower surfaces. Due to the lift force, the blade intended to go upward direction resulted into rotation of the blade along the horizontal axis [1] . The main focus of this study is to explore more detailed about the two popular performance evaluation methods: BEM and CFD. Though both approaches have advantages and disadvantages, both meth- ods are mainly established to analyze turbine performance with two different points of view. BEM method can save time for the preliminary research. Moreover, by using this approach, the design decision was made for wind turbine blade. On the other hand, CFD can provide a 3D specific idea of the flow field generated during the operation of a wind turbine. Khchine and Sriti used CFD for calculating aerodynamic characteristics of airfoil S809. Then based on those aerodynamic coefficients, they implemented BEM to predict the performance of HAWT [2] . Amano and Malloy have done their research on CFD analysis of straight spanwise and swept wind turbine blade. Though, the straight commercial blades were found very efficient at lower wind speed, from the pressure con- tour results they concluded that swept edge blade could generate more power than straight span blade [3] . Keerthana et al. have concentrated on the aerody- namic analysis of 3 kW small scale HAWT by CFD. They first configured the turbine rotor by BEM. After that, normal force, torque and power were investigated by varying wind speed at Tip speed ratio 6. From their analysis, the maximum power has been obtained at Tip speed ratio 5.8. Moreover, flow field observation was also done. They concluded that flow separation occurred at wind speed 3 m/s and 4 m/s led the lower values of normal force and torque [4] . Ano- ther investigation on BEM and CFD of HAWT was done by Dimitriadis et al.: Initially, they compared XFOIL values and CFD results for the coefficient of lift and drag. They have got that XFOIL tends to overestimate lift coefficients values. They also proved that the SST turbulence model had better accuracy than RSM turbulence model when compared with the experimental data. Finally, they ended up with the comparison of power coefficient between BEM and CFD. The authors got maximum power coefficient 0.48 by BEM and 0.42 by CFD tip speed ratio 7 [5] . Emam et al. also made a comparison between analytical method and numerical method for performance prediction of HAWT: They also compared the results of these methods with experimental data. Some induction factor correction models in BEM were intro- duced in their work. The comparison was made for power coefficient as well as for thrust coefficient. The CFD results were found to be more agreeable with the experimental values. On the other hand, among all BEM methods, Wilson correction model gave a close match with the measured values. The air velocity streamlines at flow visualization were also investigated in that study [6] . However, this running work investigated the simulated performances of small scale wind turbine blade, which was made by mixed airfoils. Here, the turbine blade was designed for small scale wind energy. The turbine blade design was performed before the performance analysis and flow visualization. Then the comparison between results which were gotten from BEM and CFD methods was made for the further analysis.
2. Wind Turbine Blade Design
Usually, the small scale lift-type wind turbine blade cross-section has single airfoil throughout the whole length. With the progress of interest in wind energy sector, some dedicated airfoils have been introduced for the wind turbine. However, for the small scale wind turbine, the airfoil should be used at a low angle of attack, where the coefficient of drag is much lower as compared to the lift coeffi- cient [7] . The selection of appropriate airfoils depends on the aerodynamic behavior and operating conditions which are related to Reynold number. The relation among the relative wind velocity, airfoil chord length, and kinematic viscosity can be defined by following equation of Reynold number.
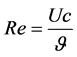 (1)
(1)
where U is relative wind velocity, c airfoil chord length, and 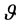 is the viscosity of air. This work focused on small scale, and in the meantime the targeted wind speed was supposed to be low. So, concentration goes to select airfoils for low Reynold number range [8] [9] . The S series airfoils are used because they are specialized for wind turbine blade and suitable for low Reynolds number. According to the suggestion given by NREL, three different parts of the wind turbine blade were designed by three different airfoils from S series [10] . In most cases, wind turbine blades include a circular segment to attach to the hub. Then a smooth, and gradual transition tapered section is located from the root to first airfoil cross-section. In general, The root side airfoil is the thickest airfoil. Then the thickness ratio gets smaller as it approaches the tip. As S823 is one of the thickest S series airfoils, it was selected for root section of the blade [11] . Then, relatively less thick S833 airfoil has been chosen for the middle part, and finally, the S822 Airfoil has been assignedfor the tip of the blade.
is the viscosity of air. This work focused on small scale, and in the meantime the targeted wind speed was supposed to be low. So, concentration goes to select airfoils for low Reynold number range [8] [9] . The S series airfoils are used because they are specialized for wind turbine blade and suitable for low Reynolds number. According to the suggestion given by NREL, three different parts of the wind turbine blade were designed by three different airfoils from S series [10] . In most cases, wind turbine blades include a circular segment to attach to the hub. Then a smooth, and gradual transition tapered section is located from the root to first airfoil cross-section. In general, The root side airfoil is the thickest airfoil. Then the thickness ratio gets smaller as it approaches the tip. As S823 is one of the thickest S series airfoils, it was selected for root section of the blade [11] . Then, relatively less thick S833 airfoil has been chosen for the middle part, and finally, the S822 Airfoil has been assignedfor the tip of the blade.
2.1. Rotor Parameters
The radius of the wind turbine rotor was selected in such a way that it fulfills the small scale criteria and as well as the expected or rated power requirement. The rotor radius was estimated from the following power equation of wind turbine.
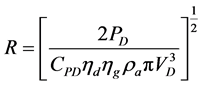 (2)
(2)
Here, 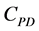 is the design power coefficient of the rotor,
is the design power coefficient of the rotor, 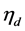 is the drive train efficiency,
is the drive train efficiency, 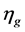 is the generator efficiency,
is the generator efficiency, 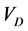 is the design wind velocity. The design power coefficient
is the design wind velocity. The design power coefficient 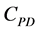 range is 0.4 to 0.5. The combined efficiency of drive train and generator is considered 0.9 [12] . The tip speed ratio is defined by the
range is 0.4 to 0.5. The combined efficiency of drive train and generator is considered 0.9 [12] . The tip speed ratio is defined by the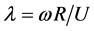 , where
, where 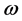 is rotor rotational speed, R is rotor radius and U is relative wind velocity [13] . In case of small scale wind turbine, tip speed ratio range 4 to 10 is recomended to maintain. According to the emperical relation between coefficient of performance and tip speed ratio, introduced by Cetin [14] , the designed tip speed ratio was selected. The proposed wind turbine fundamental design parameters and operating conditions are given in Table 1.
is rotor rotational speed, R is rotor radius and U is relative wind velocity [13] . In case of small scale wind turbine, tip speed ratio range 4 to 10 is recomended to maintain. According to the emperical relation between coefficient of performance and tip speed ratio, introduced by Cetin [14] , the designed tip speed ratio was selected. The proposed wind turbine fundamental design parameters and operating conditions are given in Table 1.
2.1. Aerodynamic Analysis
The aerodynamic behavior mainly depends on the blade design. For lower wind velocity, the blade is always designed to operate at a small angle of attack with- out flow separation. In this study, the potential flow technique was employed by using X foil software application to predict aerodynamic performance [15] . The preliminary goal of this task is to identify the appropriate angle of attack for each airfoil. In alift-type wind turbine, the optimum angle of attack is that angle of attack, when the coefficient of lift is maximum, and the coefficient of drag is the minimum. Here, three NREL S series airfoils were tested by Xfoil at designed wind speed. Figure 1 shows the selection criteria of the angle of attack with respect to the ratio of coefficient of lift and drag.
Table 1. Initial design consideration of investigated wind turbine.
Figure 1. Variation of coefficient lift drag ratio with AOA.
From Figure 1, it is showed that for the angle of attack 6˚ airfoil S833 has a maximum ratio of Coefficient of lift and drag. At another case, for airfoil S822 the coefficient of lift dominates the coefficient of drag is in maximum point at AOA 5.5˚. For the third airfoil S823, the maximum ratio happens at AOA 6.5˚. Considering all values, the optimum angle of attack for whole design blade was selected as 6˚.
2.2. Blade Geometry Criteria
Horizontal axis wind turbine blade cross-sectionsare made by airfoils which are not uniform throughout the length. The chord lengths and twist angles are varied with blade length. Excluding the hub, the total blade length was divided into nine segments. Usually, small scale wind turbine system has no pitch control unit. As the pitch angles were fixed, the twist angles of the blade in all blade segments were determined in such way that every segment has the optimum angle of attack. The following equations are used to get optimum chord length and twist angle.
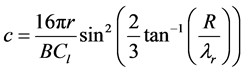 (3)
(3)
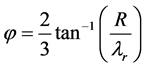 (4)
(4)
where R is rotor radius, r is local rotor radius, B is blade number, 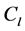 is coefficient of lift, and
is coefficient of lift, and 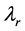 is local tip speed ratio [1] . From the hub to tip direction, the first three blade segments were designed by airfoil S823, then the following three blade segments were designed by airfoil S833 and, last three blades segments at the blade tip are made by airfoil S822. The chord lengths and twist angles with three different airfoils are given in the following Table 2.
is local tip speed ratio [1] . From the hub to tip direction, the first three blade segments were designed by airfoil S823, then the following three blade segments were designed by airfoil S833 and, last three blades segments at the blade tip are made by airfoil S822. The chord lengths and twist angles with three different airfoils are given in the following Table 2.
The above values of chord lengths and twist angles were fixedat the midpoints of the blade segments. Then, a continuous linear loft operation was done between two midpoints of blade segments, next to each other. However, this the-
Table 2. Chord length and twist angles at different sections of designed blade
oretical optimum blade chord and twist distribution sometimes are not viable for manufacturing. Because of the theoretically designed structure, there might be some complexity to manufacture the blade. For this reason, linearization of chord and twist distribution is done by several methods. However, linearization should be done in such a way that the total performance of the wind turbine will remain closer to optimum designed blade performance. Due to simplify the study, this work avoided the linearization of the blade segments parameters. However, a full wind turbine blade was modeled according to the dimensions obtained from Table 1. Figure 2 shows the blade model.
3. Performance Analysis by BEM
Integration of “Momentum-theory” and “Blade-Element-Theory” results in (BEM) analysis. Momentum-theory deals with responsible forces for producing the motion of the fluid by the rotor. On the other hand, blade element theory is related to the forces on turbine blade due to the flow of the fluid. In this method, the wind turbine blade was divided into small blade sections. After that, the conservation of one-dimensional linear momentum was applied to all segments of the blade which lead to forces and power calculation. In BEM there are two main key factors, the induction factor, and airfoil aerodynamic characteristics. The open source software Q-Blade was used to analyze the BEM [16] [17] . Here, the entire blade was divided into 40 small elements for BEM analysis. In the iterative procedure of BEM, for every element of the blade, the lift, and drag coefficients are calculated until the induction factors are expected to converge [18] . Here the axial and radial induction factors are defined as
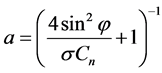 (5)
(5)

where, 
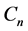


Figure 2. Proposed designed wind turbine blade.

Here, c, B, r represent chord length, blade number and local radius of the turbine blade respectively [16] . The maximum iteration for this study was set at 100. Once the convergence was done, the associated parameters were used to calculate power generated for that specific blade element. This procedure was repeatedly done for all sections of the blade. To ensure the accuracy of BEM several correction models such as new tip loss, new root loss, 3d correction, Reynold drag correction and foil interpolation were also applied in BEM [19] .
4. Performance Analysis by CFD
The CFD analysis is done based on continuity and Navier-Stokes governing equations. In this work k-ω, Shear Stress Transport (SST) turbulence model was executed in Ansys CFX software. The equations are given below
Conservation of mass is defined by

Moreover, Conservation of momentum can be represented as

where 

The blade geometry was imported into a computational fluid domain, which is one-third of a complete circular wind section around the blade. The front side and top side of the domain were defined as the air velocity inlet while rear side was defined as pressure outlet. The other two sides were assignedto the periodic boundary condition. The inlet radius of fluid domain is ten times more than the blade radius. For the outlet radius, the ratio is 20 times. The downstream length of a fluid domain is higher than upstream length which allowsobserving the generated wake in fluid domain. After that, the mesh was generated for the entire domain and as well as for the blade geometry (Figure 3).
The accuracy of the analysis depends on how the meshing is done. It is good practice to do trial and error for fixing the mesh element size, inflation layer thickness, the sphere of influence radius and so on. For better and uniform mashing the match control was applied between two periodic boundaries conditioned face. This is called local mesh control. One of the key factors of meshing is the variation of element sizing throughout the geometry. Here, the maximum and minimum face element sizes of the fluid domain are 7.47 m and 0.00747 m respectively. Besidesthis, the element size of the blade surface was maintained at 0.02 m. An inflation layer was created on the blade surface to give the better resolution of boundary layer flow. The transition ratio was maintained at 0.272 with the growth rate of 1.2. A sphere of influence was also added to fine the mesh around the blade. The sphere radius was 10 m, and element size was 0.4 m [3] [21] [22] . Figure 4 shows the cross-sectional view of imported blade geometry after applying all global and local mesh control.
Figure 3. Computational domain meshing.
Figure 4. Sectional view of blade geometry meshing.
Finally, the fluent pressure based solver was used to get aerodynamics loading, velocity streamlines, and torque generated by the blade. Here, the fluid flow was considered as turbulent. Among all the turbulence model, k-ω “Shear-Stress- Transport” (SST) model is suitable for this analysis, because it can predict the boundary layer separation under the adverse pressure gradient. Menter intro- duced this model. It is a combination of k-ε and k-ω turbulence model [23] .
The governing equations of k-ω SST model are described below


where,
The turbulence stress tensor can be defined as

The turbulence viscosity represented by

where 

The function 

Here, y denotes the distance to nearest surface
From the k-ε and k-ω turbulence model, the coefficients 





where,

Moreover, the coefficient 

However, to observe the rotational of the blade the standard moving reference frame was used. This model allows generating a steady state problem on the moving reference. Along with all standard air parameters and operating conditions, the air velocity was applied at the inlet and the top surface of the fluid domain because air flows not only from the horizontal direction but also from all direction.
5. Results
CFD post was used to observe the results of the simulation. Figure 5 shows the axial velocity of the blade tip speed ratio 6. Here, the wind velocity was main- tained at 7 m/s. Moreover, rotational velocity was maintained at 7.63 rad/s.
From the Figure 5, it is showed that the axial velocity of the blade varied throughout the blade length. The blade velocity increased from the blade root to tip. As expected with the conventional wind turbine theory the velocity of the tip is the highest velocity. It is notable that the axial velocity increased at a uniform pattern which. For this reason wind turbine blade faces centrifugal force. The air flow through the fluid domain was also observed. There is a small drop in air velocity after passing the turbine blade. The reason is the wake formation of the rotor. As compare to the all air streamline of the fluid domain, the wake formation is slight, and that can be on a negligible scale. The less wake formation leads fewer energy losses. So the currently designed wind turbine has given better performance in the point of view of wake formation. On the other hand, a sudden increase of air velocity and turbulence were observed around the tip of the blade. The reason is the blade rotational speed which fulfills the mass momentum criteria of energy conservation. Figure 6 represents the air flow visualization for designed small wind turbine rotor.
The pressure distribution on blade span wise is showed in Figure 7. It is clear that there is a clear pressure difference between upward surface and the downward face of the blade which prevails the wind turbine main aerodynamic principle. The close investigation showed that the pressure difference is higher at
Figure 5. Axial blade velocity distribution.
Figure 6. Air flow visualization.
Figure 7. Pressure distribution on blade surfaces.
outer portion compare to the inner part of the wind turbine blade. In other words, there is a low-pressure area at the tip leading edge of the blade. The reason behind this is the three-dimensional rotation effect of the wind turbine blade tip.
6. Comparison between BEM & CFD Analysis
In current study performance of wind turbine was determined against different
Figure 8. Comparison between BEM and CFD.
Tip Speed Ratio (TSR). From coefficient of performance (COP) vs. Tip Speed Ratio (TSR) curve analysis, it is clear that the performance of wind turbine blade by CFD computation is a little bit less than by BEM. The reason behind that, the CFD method can calculate more accurately with 3D calculation than BEM. Figure 6 shows that initially at low TSR the rotational speed is very low in both cases. After the TSR 3, the COP increased sharply in BEM, whether in CFD the COP increased gradually with TSR up to 5. After that, in the BEM analysis, the COP is more stable than in the CFD within the TSR range 5 to 7. For both cases, the maximum COP has gotten at TSR 6.After that, with the increasing of tip speed ratio, the coefficient of the performance went down. The reason behind this the stall condition of the wind turbine which was described by Betz limit of the windturbine. The highest coefficient of performance in BEM is 47% and in CFD method is 43%. Both of the values are within the Betz limit. The difference between both methods’ results is 4%. One of the reasons for this difference is that, the over prediction xfoil software for obtaining lift and drag coefficients. Though all kind of correction models were applied in BEM, the CFD results provided more details visualization of wind turbine response to get a complete idea about performance. The BEM has the limitation of computation for rotational motion as compared to the CFD. In CFD the predetermined aerodynamic data was not used to predict the performance. Instead of that CFD solver computed governing fluid equations at all direction around the blade by aniterative process. This approach allowed the blade to analyze any spanwise wind speed as well as the three-dimensional fluid body interaction effects including friction losses where BEM method cannot do this kind of analysis. Finally, it is con- cluded that BEM can be used for initial estimation and then the wind turbine’s design can be optimized with the detailed observation by CFD method (Figure 8).
7. Conclusion
Mixed airfoils are not usually used for a small-scale wind turbine. However, this work has shown that mixed airfoil wind turbine could also have satisfactory performance in wind energy sector. The BEM and CFD analyses were done only for the wind turbine blade. The integration of tower, rotor hub, generator housing, and yaw control has much effect on overall efficiency of the wind turbine. Instead of improving design criteria, this work focused on the performance analysis of the turbine. The further improvement of the currently designed wind turbine could be made by FSI analysis and several optimizing techniques.
Acknowledgements
Authors would express the heartiest deep sense of gratitude to reference papers, books, and websites as mentioned below which are necessary for the research.
Cite this paper
Hasan, M., El- Shahat, A. and Rahman, M. (2017) Performance Investigation of Three Combined Airfoils Bladed Small Scale Horizontal Axis wind Turbine by BEM and CFD Analysis. Journal of Power and Energy Engineering, 5, 14-27. https://doi.org/10.4236/jpee.2017.55002
References
- 1. Manwell, J.F., McGowan, J.G. and Rogers, A.L. (2010) Wind Energy Explained: Theory, Design, and Application. John Wiley & Sons, Hoboken.
- 2. Sriti, M. (2016) Performance Prediction of a Horizontal Axis Wind Turbine Using BEM and CFD Methods. In: MATEC Web of Conferences, Vol. 45, EDP Sciences.
- 3. Amano, R.S. and Malloy, R.J. (2009) CFD Analysis on Aerodynamic Design Optimization of Wind Turbine Rotor Blades. World Academy of Science, Engineering, and Technology, 60, 71-75.
- 4. Keerthana, M., Sriramkrishnan, M., Velayutham, T., Abraham, A., Rajan, S.S. and Parammasivam, K.M. (2012) Aerodynamic Analysis of a Small Horizontal Axis wind Turbine Using CFD. Journal of Wind and Engineering, 9, 14-28.
- 5. Dimitriadis, E., Missirlis, D. and Martinopoulos, G. (2014) Investigation of the Performance of a Horizontal Axis Wind Turbine with the Use of Blade Element Momentum Theory and CFD Computations. European Wind Energy Association, Barcelona.
- 6. Emam, M.K., Khalafallah, G.E. and Ahmed, A.M. (2015) A Comparative Study between Analytical and CFD Analysis for Performance Prediction of a Horizontal Axis Wind Turbine. Engineering Research Journal, 145, M1-M14.
- 7. Singh, R.K., Ahmed, M.R., Zullah, M.A. and Lee, Y.H. (2012) Design of a Low Reynolds Number Airfoil for Small Horizontal Axis Wind Turbines. Renewable Energy, 42, 66-76.
- 8. Lissaman, P.B.S. (1983) Low-Reynolds-Number Airfoils. Annual Review of Fluid Mechanics, 15, 223-239. https://doi.org/10.1146/annurev.fl.15.010183.001255
- 9. Miley, S.J. (1982) A Catalog of Low Reynolds Number Airfoil Data for Wind Turbine Applications.
- 10. Tangler, L.J. and Somers, D.M. (1995) NREL Airfoil Families for HAWTs. National Renewable Energy Laboratory.
- 11. Somers, D.M. (2005) The S822 and S823 Airfoils. National Renewable Energy Laboratory, NREL/SR-500-36342.
- 12. Mathew, S. (2006) Wind Energy: Fundamentals, Resource Analysis, and Economics. Vol. 1, Springer, Heidelberg.
- 13. Wang, L., Tang, X. and Liu, X. (2012) Optimized Chord and Twist Angle Distributions of Wind Turbine Blade Considering Reynolds Number Effects. Wind Energy: Materials, Engineering and Policies (WEMEP).
- 14. Yurdusev, M.A., Ata, R. and Cetin, N.S. (2006) Assessment of Optimum Tip Speed Ratio in Wind Turbines Using Artificial Neural Networks. Energy, 31, 2153-2161.
- 15. Drela, M. and Aero, M.I.T. (2001) Astro: XFOIL 6.94 User Guide. Harold Youngren, Aerocraft.
- 16. Marten, D. and Wendler, J. (2013) QBlade Guidelines. Ver. 0.6. Technical University of (TU Berlin), Berlin.
- 17. Marten, D., Wendler, J., Pechlivanoglou, G., Nayeri, C.N. and Paschereit, C.O. (2013) Qblade: An Open Source Tool for Design and Simulation of Horizontal and Vertical Axis Wind Turbines. International Journal of Emerging Technology and Advanced Engineering (IJETAE), 3, 264-269.
- 18. Sorensen, J.N. (2015) General Momentum Theory for Horizontal Axis Wind Turbines. Vol. 4, Springer, Berlin.
- 19. Tenguria, N., Mittal, N.D. and Ahmed, S. (2010) Investigation of Blade Perfor- mance of Horizontal Axis Wind Turbine Based on Blade Element Momentum Theory (BEMT) Using NACA Airfoils. International Journal of Engineering Science, 2, 25-35.
- 20. Fluent, A. (2009) User’s Guide. Fluent Inc., New Hampshire.
- 21. Hartwanger, D. and Horvat, A. (2008) 3D Modeling of a Wind Turbine Using CFD. NAFEMS Conference.
- 22. Wang, L., Quant, R. and Kolios, A. (2016) Fluid-Structure Interaction Modeling of Horizontal-Axis Wind Turbine Blades Based on CFD and FEA. Journal of Wind Engineering and Industrial Aerodynamics, 158, 11-25.
- 23. Douvi, E.C. and Margaris, D.P. (2014) Computational Study of the Flow over a Horizontal Axis Wind Turbine. 6th International Conference from Scientific Computing to Computational Engineering (6th IC-SCCE), Athens.











