Journal of Power and Energy Engineering
Vol.03 No.11(2015), Article ID:61256,15 pages
10.4236/jpee.2015.311002
Toward an Evolutionary Multi-Criteria Model for the Analysis and Estimation of Wind Potential
Fouad Amri, Omar Bouattane, Tajeddine Khalili, Abdelhadi Raihani, Abdelkader Bifadene
Lab SSDIA, ENSET Mohammedia, Hassan II University of Casablanca, Casablanca, Morocco

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 October 2015; accepted 16 November 2015; published 19 November 2015
ABSTRACT
The main objective of this paper is to model, analyze and estimate wind energy at East region of Mohammedia and other Moroccan sites. The basic data were taken from meteorological records of each region. In this context, this work is focused on a methodological approach of a decision sup- port system for optimal choice of wind turbine using multi-criteria model that takes into consi- deration both the accurate Weibull distribution in the area (wind speed-ground roughness) and the technical parameters of the wind turbine. In this approach we realized an adapted modeling of each element of the turbine (rotor-multiplier-generator). This article also offers a way to forecast wind speed in a region where wind data are not accessible using an artificial neural network.
Keywords:
Wind Potential, Meteorological Records, Energy Production, Weibull Statistical Distribution

1. Introduction
The wind is a promising sustainable energy source that can help reduce dependence on fossil fuels. Wind power has a very high world growth rate. In 2013 wind power worldwide grew by 35,572 MW, bringing the global installed capacity to over 318 GW [1] [2] . Although it can’t replace completely the traditional energy sources, this energy can however offer an interesting renewable alternative that would help to reduce the exhaustion of fossil resources. It fits perfectly in the global effort to reduce CO2 emissions and more generally in the context of sustainable development of the energy landscape. Choosing a wind farm in a wind energy production system is the most crucial part because the energy produced depends essentially on the wind resources available at the site. In order to achieve an accurate estimation of these resources, the implementation of a high performance computing tool is required to avoid wind intermittency misguidance [3] . In the first part of this paper we represented the wind speed probability distribution using Weibull distribution to estimate and analyze the energetic wind potential in many Moroccan sites. In the second part, we propose a decision support system model for an optimal choice of wind turbine technology using multi-criteria model that takes into account both the best Weibull distribution in a given location and the appropriate wind turbine. When wind speed data are not available in a given location we elaborated an artificial neural network that predicts wind speed records.
2. The Wind Analysis
In literature many probability density functions may be used to study the wind speed, although the most widespread is the Weibull distribution as it is more accurate in this field. According to Justus et al. [4] , the Weibull distribution with two parameters is given by the following equation [4] [5] :
 (1)
(1)
where c (m/s) is the scale parameter that determinates the position of the curve, based on wind characteristics in the site, and k (unit less) is a shape parameter that indicates the shape of the curve, and v is the wind speed. There are several methods to estimate the c and k parameters of the Weibull distribution: the Standard deviation method (SD), the Method of maximum likelihood (MLH) and the least squares method (LSM). In this study, the two parameters k and c were determined using the SD, given by:
 (2)
(2)
 (3)
(3)
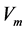 is the average speed, σ the standard deviation and
is the average speed, σ the standard deviation and 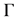 is the usual gamma function.
is the usual gamma function.
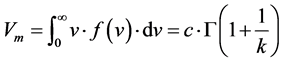 (4)
(4)
In this study the wind speed data was collected at different heights , it is then necessary to extrapolate the measures at a same height H.
, it is then necessary to extrapolate the measures at a same height H.
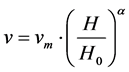 (5)
(5)
where  the surface roughness and v is the wind speed at the desired height.
the surface roughness and v is the wind speed at the desired height.
2.1. Wind Power Density
The wind power flowing at a speed v through the blade sweep area A [m2] is given by the well known expression [6] :
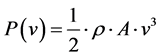 (6)
(6)
The wind power density, for a given theoretical probability distribution , can be calculated by the following integration:
, can be calculated by the following integration:
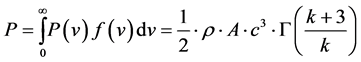 (7)
(7)
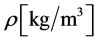 is the air density.
is the air density.
2.2. Available Wind Energy Density Estimation
Likewise, the available energy per year 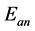 [W×h] is given by:
[W×h] is given by:
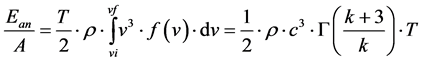 (8)
(8)



2.3. Wind Available Energy Estimation Results
The following results were obtained for the site of the ENSET Mohammedia and many other sites in the Moroccan territory, based on meteorological data. Owing to the fact that Sites in our study can be classified into three different types as explained further, we picked a site from every class to represent the Weibull distribution, as shown in Figures 1-3, while Table 1 summarizes all the results.
The average wind speed, the Weibull parameters c and k, the wind power density and the available wind energy density, represented in Figures 1-3 and Table 1, are the essential factors affecting site choice. As shown in Table 1, the most promising sites in terms of available wind energy density are: El Koudia Al Baida (Teto- uan), Sendouk (Tanger), Cap Sim (Essaouira) Col Touahar (Taza), S. EL Garn (Tantan), Tarfaya, Laayoune,
Figure 1. Histogram and Weibull distribution of wind speeds (Site: Col de Touahar Taza).
Figure 2. Histogram and Weibull distribution of wind speeds (Site: Had hrara Safi).
Figure 3. Histogram and Weibull distribution of wind speeds (station ENSET Mohammedia).
Table 1. Wind available energy estimation results.
Tiniguir (Dakhala), therefore these locations are the most suited for wind farms.
Moulay Bousselham (Kenitra), Had hrara (Safi), Salouane (Nador) have a low average wind potential, which makes these location non suitable for massive wind farms and big wind turbines, however they can be very good spots for the installation of small wind turbines not exceeding 400 KW. The wind turbine installed in ENSET Mohammedia for example is destined to scientific research purpose, and is of domestic size because of the low potential in this region.
2.4. Selecting Best Fit Wind Turbines
The geographic location and wind turbine generator selection affect directly the wind farm economics. Appro- priate wind turbine generators are chosen based on the annual energy production. As a first step we estimate the power production for many wind turbines, in order to choose the best matching one for each site in our study. Figure 4 shows the curves of rated power of the first category of wind turbines: V52-850 KW, V80-2000 KW and V112-3000 KW. This type of wind turbines is destined to sites that are the most qualified for wind farms. For sites with moderate potential we decided to compare more adapted types of wind turbines: E33-335 KW, E40-600KW, and E44-910KW (Figure 5). In the ENSET Mohammedia region which has the lowest potential
Figure 4. Power curves of Vestas wind turbines.
Figure 5. Power curves of Enercon wind turbines.
we used smaller wind turbines. All power curves were obtained from constructor data sheets.
In an attempt to identify the most efficient wind turbine in each site, we were forced to compute a yield factor (



In Table 2, we summarized computed values of the yield factor for each wind turbine. We noticed that efficient choice of the wind turbine is not established only by its annual production. Therefore in the 8 first sites the V80-2MW with an average annual energy production is the most effective investment, because it has the highest yield factor. On the same basis, the E33-335KW is the most adequate wind turbine for sites with average potential. Likewise in the ENSET station, the optimal wind turbine is the Ws-3,2KW.
3. Modeling of the Wind Turbine
In order to enhance the decision support system it is necessary to model the principal wind turbine components, using the V-80 as it appears to be the optimum choice in the windiest sites. In an aim to aggregate our decision system the following models (corresponding to the four main components of a horizontal axis wind turbine) were taken into account in our study for the modeling of the wind turbine.
3.1. Rotor Model
The power that can be produced by a wind turbine at every speed v is given by [3] :
Table 2. Annual energy and Yield factors.

Cp is the power coefficient of the rotor which can be estimated by [8] [9] :








where
B is the number of pales.


3.2. Gearbox Model
Total Gearbox efficiency 






3.3. Generator Model
The total power 

The total efficiency of the generator is given by [11] [12] :

With:



SCS is the stall-constant-speed, PCS is the pitch-constant-speed and PVS is the pitch-variable-speed.
By combining the three component models presented above we get the overall power coefficient:

Once the total power coefficient determined, it is now possible to calculate the annual electric energy production.
3.4. Energy Model
The annual production of electrical energy 


where 


The boundary layer is the energy exchange area between the atmosphere and the land surface. The Weibull parameters c and k depend of the site characteristics. With these parameters and the height of the hub Hhub, it is possible to define the new Weibull parameters 



with:





4. Results and Discussion
Our decision support model aim to select the optimal wind turbine technology at a specific location, in order to minimize cost and maximize benefits by selecting the most homogenous correlation between technical gear and geographic location. To achieve this objective we developed a method including input variables that represent the technical characteristics of the wind turbines, and other input variables representative of the wind energy available in the site computed from the wind model.
The evolution of the power coefficient 
Figure 6 represents a Comparison between the power curve given by the manufacturer and the one computed by the model. The wind power curve shows that between the starting speed and nominal wind speed, the machine extracts the maximum power of wind on the rotor disc, as the two curves are matching. We notice that the two power curves are different for high speeds; this is due to the mechanical constraints that are applied on pales, it is necessary to block the wind turbine running in case of high wind speed.
In Figure 7, we plotted the power coefficient provided by (17).
Knowing the total power coefficient, it is possible to calculate the annual electric energy produced. Thus, we took the site Col de Touahar as an example for detailed study with the wind turbine V80-2MW, and we summarized the rest in the Table 5.
- Site: Col de Touahar
First we carefully realized an extrapolation of Weibull parameters at the Hub height given by the Table 4. The Weibull distribution at the Hub height is plotted in the Figure 8.
According to Equation (18), annual energy produced can be calculated per year for this site:

5. The Artificial Neural Network (ANN) to Forecast Wind Speed in Other Regions in Morocco
Our study took into consideration many sites in Morocco; however our model and the data acquired are not sufficient to provide results in sites where the wind speed data is not available. In an attempt to predict the wind speed in regions where data is missing or not complete, we realized an artificial neural network to forecast monthly wind speed in the region of Boujdour as an example of location where metrological instrumentation is not available [13] . Our ANN Figure 9 establishes a correspondence between longitude, latitude, temperature, elevation and wind speed, based on measures gathered from 21 stations inside the Moroccan territory.
The ANN used is a multilayer Perceptron (MLP) type that provides FeedForward architecture [14] [15] ; the input and output layer are respectively constituted of 4 and 12 neurons respectively, the hidden layer contains 20
Table 3. Wind turbine design variables.
Figure 6. Power, comparison of model results with measured data for wind turbine V-80.
Figure 7. Coefficient of maximum power for wind turbine as obtained by Equation (17).
Figure 8. Weibull distribution of wind speeds at the hub height Site “Col de Touahar”.
Figure 9. Conceptual idea of the built artificial neural network.
Table 4. The site characteristics at the hub height: Col de Touahar.
Table 5. The results of the wind energy available at hub height.
neurons. This configuration is optimal because we can get a minimal error 

Where, 

d and y are successively the target value and the value produced by the perceptron.
Geographical coordinates Table 6: longitude, latitude, altitude, and average temperature monthly observed represent the input for the ANN used in this study.
Temperatures used for this study, displayed in Table 7, are the average monthly recorded degrees token from the NASA: Atmospheric Science Data Center [17] .
The average wind speed recorded monthly from several years of data Table 8 in the 21 sites used for this ANN approach will be in the output layer.
The data collected in the previous table was also collected at different heights, it is then also necessary to extrapolate the measures at a same height too, using the relation (5). We will use the same relation (21) to get the surface roughness. Table 9 summarizes the results obtained after extrapolation to 10 meters.
Normalization is a very important procedure in the training phase and the testing of the artificial neural network, because it guarantees that outputs and inputs are on the same weight scale [18] . Data was normalized linearly in order to values ranging from 0 to 1 using the following relation:

Predicted wind speed results in the unknown site of Boujdour, using the ANN for a height of 10 m like the data used before are displayed in Table 10.
As performed previously we can extrapolate the obtained results to a desired height, we give the following
Table 6. Geographical coordinates of the different sites used for the study [2] .
Figure 10. Plotted wind speed data obtained by the ANN for Boujdour.
Table 7. Temperaturesused for the study [17] .
Table 8. Average wind speed recorded monthly used for the study [2] .
Table 9. Results obtained after extrapolation to 10 meters.
Table 10. Wind speed Results obtained by the ANN at a height of 10 m.
Table 11. Extrapolated wind speed Results obtained by the ANN at a height 20, 30, 40 m.
extrapolated data at different heights (20, 30, 40 m), Table 11 summarizes the results, Figure 10 displays the wind velocity prediction for the four different heights.
In this part we obtained the wind speed data in a region where it was impossible to get wind speed records.
The artificial neural network used has proven its reliability in predicting wind speed for the site of Boujdour. This approach allowed us to get the missing wind data, which is the most important parameter in our decision support system for optimal choice of wind turbine, when obtained; the process of assessing wind potential in order to install the right technology can be continued using the same procedure.
6. Conclusions
In this study, we have modeled and evaluated the available wind energy per year in many Moroccan sites. To achieve this objective, we have modeled the wind speed data using the Weibull probability density function and determined values for both the shape and scale parameters, in order to estimate wind energy potentials for the each studied location. Those parameters were extrapolated at a same height to assess the available wind potential in these sites.
Thus, we can classify the studied areas into three categories: the greatest wind potential regions, the medium potential regions, and the lowest potential regions, like the ENSET Mohammedia station, where the average wind speed and the available energy do not exceed respectively 2.61 (m/s) and 420.3 (KWh/m2).
Through this study, we could choose the appropriate wind turbine for each site. Medium wind potential
regions like Moulay Bousselham (Kenitra), and salouane (Nador) are not suited for the installation of big turbines but can accommodate wind turbine not exceeding 400 KW.
Sites of Al Koudia Al Baida (Tetouan) Sendouk (Tanger), Cap Sim (Essaouira) and Col de Touahar (Taza) have very substantial wind resources with an average annual wind speeds between 8 and 11 (m/s). The energy
that can be produced in these sites using the V80-2MW wind turbine model is between 9935.36 and 13354.7 MWh, which makes them more suited for the installation of wind farms for electricity production connected to the national grid. This study has also shown that when wind speed data are not available in regions like Boujdour, the use of an artificial neural network designed to predict wind speed records can be a very reliable forecasting tool.
In terms of perspectives our prime objective is to propose effective methods to forecast wind speed in real time. This very important wind-related engineering topic is crucial in the right management of a wind farm.
Cite this paper
Fouad Amri,Omar Bouattane,Tajeddine Khalili,Abdelhadi Raihani,Abdelkader Bifadene, (2015) Toward an Evolutionary Multi-Criteria Model for the Analysis and Estimation of Wind Potential. Journal of Power and Energy Engineering,03,14-28. doi: 10.4236/jpee.2015.311002
References
- 1. Wind Energy Barometer. EUROBSERV'ER, February 2014.
http://www.energies-renouvelables.org/observ-er/stat_baro/observ/baro-jde14-gb.pdf - 2. Enzili, M., Affani, F. and Nayssa, A. (2007) Les ressources éoliennes du Maroc.
- 3. Ouammi, A., Ghigliotti, V., Robba, M., et al. (2012) A Decision Support System for the Optimal Exploitation of Wind Energy on Regional Scale. Renewable Energy, 37, 299-309.
http://dx.doi.org/10.1016/j.renene.2011.06.027 - 4. Justus, C.G., Hargraves, W.R. and Yalcin, A. (1976) Nationwide Assessment of Potential Output from Wind-Powered Generators. Journal of Applied Meteorology, 15, 673-678.
http://dx.doi.org/10.1175/1520-0450(1976)015%3C0673:naopof%3E2.0.co;2 - 5. Gualtieri, G. and Secci, S. (2012) Methods to Extrapolate Wind Resource to the Turbine Hub Height Based on Power Law: A 1-h Wind Speed vs. Weibull Distribution Extrapolation Comparison. Renewable Energy, 43, 183-200.
http://dx.doi.org/10.1016/j.renene.2011.12.022 - 6. Diveux, T., Sebastian, P., Bernard, D., et al. (2001) Horizontal Axis Wind Turbine Systems: Optimization Using Genetic Algorithms. Wind Energy, 4, 151-171.
http://dx.doi.org/10.1002/we.51 - 7. Ouammi, A., Dagdougui, H., Sacile, R., et al. (2010) Monthly and Seasonal Assessment of Wind Energy Characteristics at Four Monitored Locations in Liguria Region (Italy). Renewable and Sustainable Energy Reviews, 14, 1959-1968.
http://dx.doi.org/10.1016/j.rser.2010.04.015 - 8. Kiranoudis, C.T. and Maroulis, Z.B. (1997) Effective Short-Cut Modelling of Wind Park Efficiency. Renewable Energy, 11, 439-457.
http://dx.doi.org/10.1016/s0960-1481 (97)00011-6 - 9. Kiranoudis, C.T., Voros, N.G. and Maroulis, Z.B. (2001) Short-Cut Design of Wind Farms. Energy Policy, 29, 567-578.
http://dx.doi.org/10.1016/s0301-4215 (00)00150-6 - 10. Arbaoui, A. (2006) Aide à la décision pour la définition d'un système éolien, adéquation au site et à un réseau faible. Thèse de Doctorat, ENSAM, Paris.
https://tel.archives-ouvertes.fr/pastel-00002722/document - 11. Harrison, R. and Jenkins, G. (1994) Cost Modelling of Horizontal Axis Wind Turbines (Phase 2). ETSU W/34/00170/ REP, University of Sunderland, Sunderland.
http://www.opengrey.eu/item/display/10068/633220 - 12. Harrison, R., Jenkins, G. and Taylor, R.J. (1989) Cost Modelling of Horizontal Axis Wind Turbines—Results and Conclusions. Wind Engineering, 13, 315-323.
http://www.opengrey.eu/item/display/10068/633220 - 13. Ouammi, A., Zejli, D., Dagdougui, H. and Benchrifa, R. (2012) Artificial Neural Network Analysis of Moroccan Solar Potential. Renewable and Sustainable Energy Reviews, 16, 4876-4889.
http://dx.doi.org/10.1016/j.rser.2012.03.071 - 14. Ata, R. (2015) Artificial Neural Networks Applications in Wind Energy Systems: A Review. Renewable and Sustainable Energy Reviews, 49, 534-562.
http://dx.doi.org/10.1016/j.rser.2015.04.166 - 15. Gardner, M.W. and Dorling, S.R. (1998) Artificial Neural Networks (the Multilayer Perceptron)—A Review of Applications in the Atmospheric Sciences. Atmospheric Environment, 32, 2627-2636.
http://dx.doi.org/10.1016/s1352-2310(97)00447-0 - 16. Velo, R., López, P. and Maseda, F. (2014) Wind Speed Estimation Using Multilayer Perceptron. Energy Conversion and Management, 81, 1-9.
http://dx.doi.org/10.1016/j.enconman.2014.02.017 - 17. NASA Atmospheric Science Data Center.
http://eosweb.larc.nasa.gov - 18. Chaturvedi, D.K. (2008) Soft Computing. Studies in Computational Intelligence, 103.
http://dx.doi.org/10.1007/978-3-540-77481-5














