Journal of Power and Energy Engineering
Vol.02 No.11(2014), Article ID:51349,9 pages
10.4236/jpee.2014.211002
Capacitance of Water Tree Modeling in Underground Cables
Qi Chen, Klaehn Burkes, Elham Makram*, Ramtin Hadidi, Xufeng Xu
Department of Electrical Engineering, Clemson University, Clemson, USA
Email: *qic@clemson.edu
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 September 2014; revised 20 October 2014; accepted 3 November 2014
ABSTRACT
Water Tree is a corrosion phenomenon in cross-link polyethylene (XLPE) insulation. It is commonly found in underground cables. Water tree induced fault is difficult to detect due to its high impedance and difficult to model due to its random nature. In recent years, underground cables have become more popular in the power industry. They are resistant to environmental damage and has reduced space requirement. They are suitable to areas with high environment hazard or heavily populated areas where space is a constraining factor. As a result, studying and modeling the structure and effect of water tree become increasingly important. Since majority of the fault inducing water trees are vented trees which originated from the surface of the cable insulation, the mathematical model focuses on this particular type of water tree. To reduce the complexity of the model, the shape of the water tree afflicted region of the insulation is assumed to be ellipsoidal and the permittivity of the region is assumed to be linearly changing. Finite element analysis is used to analyze the water tree affected region. The resultant capacitance is calculated and compared with a physical model from Comsol. The result obtained using the proposed mathematical model and the result obtained using physical simulation through Comsol package agrees with each other. Hence, this method can be used to analyze the effect of water tree fault in large power systems.
Keywords:
Water Tree, Vented Tree, Finite Elemental Analysis, Capacitance

1. Introduction
Traditionally, overhead transmission lines have been the overwhelmingly popular choice in power industry. It is cheap, simple to install and easy to maintain. However, the popularity of underground cables has been on the rise in the recent years. Underground cables offer some important advantages over the overhead lines. In some situations, these advantages are sufficient to offset the inherent higher cost of underground cables. One such advantage is resistance to environmental damage such as hurricane and flood [1] . Other benefits also include space saving in locations with high population density.
However, operating and maintaining underground cable is a complex endeavor, especially during the fault rectification process. During this process, the ground has to be excavated and the associated high cost necessitates alternative fault location methods to visual inspection. To this purpose, a number of methods have been developed in the past. They use voltage and current readings from terminal ends of the cable segment to estimate the fault location. These methods include tan-delta, and traveling wave [2] -[8] .
However, the existing techniques are often unreliable when detecting water tree related faults. Water tree is an erosion phenomenon typically found in the underground cables. When underground cables are subjected to environment with high level of humidity (>65%), the insulation layer may begin to break down [9] . The process is slow and often requires decades to develop. As a result, water tree is generally found in older cables. Many of these old cables are already in hard-to-reach locations. Their repair processes are expensive and time consuming. Therefore, it becomes necessary to develop mathematical models for water trees. So their effect on the system can be better studied. The models can also be used to develop detection techniques for water tree faults and reduce the cost of underground cable maintenance.
Water tree consists of clusters of small tube-shaped water pathways referred as branches. The diameter of these branches is in the range between 5 to 300 micrometers [10] . Due to its small cross section area, the resistance associated with water tree branches is extremely high; due to its overall small area in cable insulation, the capacitance associated with water tree is extremely small. The high resistance and small capacitance of water tree result in higher fault impedance than typical high impedance faults. Since detection techniques rely on observing a response from the fault itself, high impedance significantly reduces the magnitude of the response and renders the traditional methods less effective.
Aside from its high impedance, water tree structure is also highly random. Water tree growth is subjected to a large number of environment factors. Laboratory cable aging experiments under controlled environment have proved that even under identical conditions, the water trees developed still have a wide range of branch numbers and lengths [11] . The randomness in water tree development makes model development a challenge.
Several steps can be taken to reduce the difficulty of water tree modeling. First of all, there are characteristics common to all water trees. By using appropriate assumptions, the randomness in the model can be reduced. Second, by dividing water tree structure into small, individual elements, the property of water tree afflicted insulation becomes uniform. Thus, by applying finite element analysis technique to the water tree structure, a mathematic model can be developed for the capacitance change associated with water tree development.
2. Water Tree Characteristics and Development
2.1. Physical Characteristics of Water Tree
Due to the random nature of water tree development, water trees may develop into a number of different shapes. However, depending on the overall shape, location of origination and specific shape, there are six general types of water tree as shown in Figure 1.
All water trees fall under two overall shapes: vented trees and bow tie trees. Vented Tree will grow from the surface of the insulation and develop only in one direction. Bow-tie tree will grow from inside of the insulation and develop towards two different paths as shown in Figure 2.
Since majority of the bow-tie trees are caused by manufacturing defect within the cable insulation, they are not distinguished by their locations of origination. In comparison, vented trees are separated into two types depending on their locations of origination. The first type of vented trees originates from the inner surface of the cable insulation and grows from the conductor to the outer surface of cable. This type of water tree is often caused by manufacturing defects of the conductor. The second type of vented trees originates from the outer surface of the cable insulation and grows towards the conductor. This type of tree is typically caused by external damage and age. It is the dominant form of water tree in older cables.
The third factor, specific shape, depends on the frequency (more specifically, the number of times which the magnitude of the electric field crosses zero) of the electric field experienced by the water tree during its development process [10] .
Figure 1. General types of water tree.
Figure 2. Overall shape of water tree.
2.2. Water Corrosion Process
The fundamental force behind water tree growth is the electric field. In general, stronger field strength results in longer tree branches. However, water trees are different from electrical trees caused by overvoltage insulation breakdown. The mechanism behind water tree development can be observed from interaction between water and AC electric field found in medical sprays [12] . It is observed that when a water surface is subjected to time varying electric fields, it will produce droplets in the form of micro-jets. Micro-jet is a phenomenon where charge-neutral water droplets are continuously propelled towards a fixed direction as shown in Figure 3.
It is theorized that when a material interface exists (such as water/air or water/XLPE interface), a time varying electric field will generate a frequency dependent Maxwell-Wagner force along a fixed direction.
In the case of cables, if cable insulation is damaged and sufficient amount of water is present, a water/XLPE interface will form and Maxwell-Wagner force may develop along certain directions. This hypothesis is supported by field observations where water tree develops much more rapidly when the cable surface is sanded. Furthermore, laboratory experiments confirmed that water tree will not develop if there is insufficient amount of moisture (less than 60% humidity) [9] .
In the past, researchers have speculated the relationship between the time varying electric field and water tree growth [10] . It is observed that instead of the frequency of the field, the predominant factor in determining the shape of the water tree is the number of zero-crossing of the field. When the applied voltage is a combination of two waves of different frequencies, if the overall electric field has more zero crossings, then the water tree cluster will become spread-out, resulting in a hand shaped tree. In contrast, if there is less zero crossing, then the tree cluster will be more concentrated. This results in a ball shaped tree as shown in Figure 4.
2.3. Characteristic of Water Tree Fault
As stated in the introduction, one of the defining characteristics of a water tree fault is its high impedance. While water tree fault may superficially resemble single line to ground faults (SLGF), its fault impedance is significantly higher than the typical SLGF. As a result, the fault current and voltage drop associated with a water tree is extremely small.
In fact, if weather condition of the area is dry or the service voltage is low, the water tree fault may not occur, even after water tree has already completely breached the insulation [9] . This is because water tree branches exist as strings of ellipsoidal shaped micro-fractures. These fractures can open and close according to Maxwell-Wagner force, thus cutting off the conductive pathways. Alternatively, in dry environment, the water channels may evaporate completely and cut off the fault current flow.
Consequently, the main challenge associated with water tree fault is proper detection and identification of these high impedance faults.
Figure 3. Water surface ejecting micro-jets under AC field.
Figure 4. Specific shape of water tree.
3. Modeling Water Tree Induced Capacitance Change
A major challenge in modeling water tree is that the exact structure of water tree is very difficult to predict. Even under controlled laboratory conditions, individual XLPE cables will develop different water tree structures [11] . However, all water trees structures follow certain patterns. By utilizing these patterns and appropriate assumptions, water tree may be treated as lumped elements in a power system study.
3.1. Basic Structure: Water Tree Afflicted Cable Segment as Cylindrical Capacitor
In order to model water tree appropriately, the following assumptions are made:
1) The water tree develops from outer surface of the insulation from a single point. Under this assumption, the tree will be a vented tree originated from the outer surface of the insulation as shown in Figure 5.
This particular water tree orientation is chosen since this is the most dangerous and difficult to detect type of tree in real world applications. In section II, part B, it is mentioned that the driving force of water tree development is the electric field. The rate of tree development is closely related to the electric field strength. Stronger electric field causes faster growth and tree growth may stagnate if the field strength falls below certain threshold. In the case of bow-tie trees and vented trees originated from the conductor, their branches will grow away from the conductor and experience gradually weakening electric field. In practice, majority of these trees will eventually stop developing. Vented trees originated from the surface, on the other hand, will experience stronger and stronger electric field as it grows. As a result, this type of tree is responsible for majority of water tree related faults.
2) The second assumption is that the water tree cluster is bounded within an ellipsoid shaped area as shown by the dashed lines in Figure 5. This is because in a stable power grid, the power cables will be operating at 60 Hz (alternatively, 50 Hz for European grids) with relatively small amount of harmonics throughout majority of its operational life-span. Experimental results from Maeda et al. [10] shows that at this frequency and low harmonics, the water tree shape is likely to be a ball-shaped tree as shown in Figure 4; therefore, the best way to represent the water tree cluster will be an ellipsoid shaped bounded region.
3) The ellipsoid shaped area is assumed to be a dielectric material with a linearly changing permittivity along its central axis as depicted in Koo et al. [13] . It also has a linear changing permittivity from the edge of the bounded area to the central axis as depicted by Chen and Filippini [14] . At the base of the area, the relative per-
Figure 5. Water tree structure assumption.
mittivity is assumed to be 6.9. At the tip of the area, the relative permittivity is assumed be 2.3. Under assumption 1 and 2, the water tree branches will likely to have a uniform distribution density. The thickest branches will be located at the base of the area and smallest branches at the tip; therefore, the permittivity at the tip of the water tree will be approximately the same as healthy XLPE insulation (which has a relative permittivity of 2.3). The relative permittivity of 6.9 at the base of the area is an empirically value from field observations. Using the same approach, the water tree branches at the edge of the bounded area will be small and their concentration will be low. As a result, the relative permittivity at the edge of the bounded area will also be 2.3. This permittivity will change horizontally from the edge to the central axis.
Under these assumptions, the cable capacitance can be represented as a cylindrical capacitor with multiple dielectrics. Figure 6 shows an example of such capacitor with two dielectric materials. 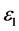 and
and 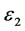 represent permittivity of two different dielectric materials:
represent permittivity of two different dielectric materials:
The capacitance of this capacitor is shown below:
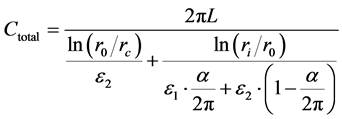 (1)
(1)
where:
L is the length of the segment;
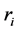 is the radius of the cable;
is the radius of the cable;
 is the radius of the inner ring of insulation;
is the radius of the inner ring of insulation;
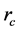 is the radius of the conductor;
is the radius of the conductor;
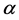 is the angle of the area with permittivity of
is the angle of the area with permittivity of 
3.2. Finite Element Analysis of Water Tree Afflict Region
Since the water tree structure is significantly more complex than a capacitor with multiple dielectric materials, the cylindrical capacitor model needs to be modified to analyze the water tree shown in Figure 5. The dielectric material with permittivity 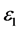 in Figure 6 is used to represent insulation layer afflicted with water tree. The dielectric material with permittivity
in Figure 6 is used to represent insulation layer afflicted with water tree. The dielectric material with permittivity  is used to represent healthy insulation layer.
is used to represent healthy insulation layer.
By using finite element analysis technique, large and complex structures and shapes can be broken down to smaller and simpler to solve elements; therefore, the pie shaped section in Figure 6 can be broken down into smaller piece as shown in Figure 7:
Where:
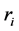 is the radius of the cable;
is the radius of the cable;


In order to break down the ellipsoid shape into concentric pieces that can be calculated using the cylindrical capacitor method, the cable insulation is separated into layers. Each layer is a concentric ring centered at the conductor. With sufficient number of layers, ellipsoid region becomes a component which occupies α_i/2π portion of the concentric ring as shown in Figure 8.
Figure 6. Simple cylindrical capacitor with two dielectric material.
Figure 7. Finite element analysis of the ellipsoid shape.
Figure 8. FEM breakdown of ellipsoid shape.


In this analysis, the solved capacitance will be divided into two portions: capacitance of healthy insulation and capacitance of water tree affected insulation.
4. Work Case Result
4.1. Result from the Mathematical Model
The capacitance of the cable will be divided into two distinct elements as shown in Figure 9.
The capacitor 

Figure 10 shows the simulation result of 
A comparison is drawn in this simulation. The 

According to the simulation, while the two curves are different, the difference in their absolute magnitude is in the range of nF/m. This comparison reflects the fundamental problem associated with water tree detection. The difference between healthy and water afflicted insulation is so small that most instruments are simply not sensitive enough to detect it.
Figure 11 shows the overall capacitance of the insulation at different stages of Corrosion:
From simulation, it can be observed that while there is a change in cable capacitance as water tree grows, the value of capacitance change is relatively small, especially considering the fact that the length of water tree affected cable segment is often on the scale of 1 centimeter or less.
4.2. Comsol Model
In order to verify the accuracy of the mathematical model, a physical simulation is done in Comsol for comparison purpose [15] [16] . The Comsol physical simulation model is shown below in Figure 12. The water affected area is presented as a region of insulation material with linearly changing electric permittivity.
Figure 12 represents the electric field of cable cross section. The water tree affected area is located on the top
Figure 9. Equivalent circuit simulated capacitance.
Figure 10. Capacitance of water affected area.
Figure 11. Overall capacitance.
Figure 12. Comsol simulation result.
of the picture. From Figure 12, it can be observed that the electric field in the region associated with water tree is altered. By measuring the leakage current, capacitance valuesare obtained from the Comsolphysical model. The results from the Comsol simulation match the capacitance of the water affected area results from Figure 10.
5. Conclusions
As underground cables become more prevalent in power grid, the effect of water tree on the power industry becomes more pronounced; therefore, it becomes necessary to establish mathematical models that could be used to analyze the effect of water in the power system.
Since many environmental, operational and manufacturing factors can contribute to water tree development, its structure is highly random and difficult to predict. As a result, assumptions must be made in order to analyze and develop a mathematic model for water tree, such as location of the water, approximate area of the water and tree branch distribution.
Under these assumptions, the mathematical model is developed for balled shaped vented tree originated from surface of cable insulation using finite element analysis. The result from the mathematical model is compared with Comsol simulations using a physical model. The results match each other.
The work case result can be potentially used in system studies such as transient analysis. Due to its slow development rate, water trees can be assumed to act as system components with a fixed resistance and capacitance in short term studies. The Comsol simulation confirms this assumption. In this case, the model can be used to estimate the capacitance value associated with the water tree.
In the future, research should be taken to expand the model to include non-linear electric permittivity distribution of the water tree affected region. In the current model, the permittivity of the region is assumed to be linearly changing. However, the field cases may not follow this assumption. For example, non-uniform distribution of water tree branches may cause the permittivity of the water tree afflicted region to change non-linearly. The scopes of the future studies should include the effects of these irregularities on water tree behaviors in large power systems.
References
- Xu, L. and Brown, R.E. (2009) A Framework of Cost-Benefit Analysis for Overhead-to-Underground Conversions in Florida. Power & Energy Society General Meeting, 2009. PES '09. IEEE, Calgary, 26-30 July 2009, 1-7. http://dx.doi.org/10.1109/PES.2009.5275583
- Park, S.-H., Jung, H.-E., Yun, J.-H., Kim, B.-C., Kang, S.-H. and Lim, K.-J. (2008) Classification of Defects and Evaluation of Electrical Tree Degradation in Cable Insulation Using Pattern Recognition Method and Weibull Process of Partial Discharge. International Conference on Condition Monitoring and Diagnosis, 2008. CMD 2008, 21-24 April 2008, Beijing, 101-104. http://dx.doi.org/10.1109/CMD.2008.4580240
- Lee, J.D., Ryoo, H.S., Choi, S.B., Nam, K.Y., Jeong, S.H. and Kim, D.K. (2006) H/W Desig for Fault Location System on Underground Power Cable. Transmission and Distribution Conference and Exhibition, 2005/2006 IEEE PES, 21-24 May 2006, Dallas, 843-846. http://dx.doi.org/10.1109/TDC.2006.1668607
- Ponniran, A. and Kamarudin, M.S. (2008) Study on the Performance of Underground XLPE Cables in Service Based on Tan Delta and Capacitance Measurements. Power and Energy Conference, 2008. PECon 2008. IEEE 2nd International, 1-3 December 2008, Johor Bahru, 39-43. http://dx.doi.org/10.1109/PECON.2008.4762442
- Livie, J., Gale, P. and Wang, A.D. (2008) The Application of On-Line Travelling Wave Techniques in the Location of Intermittent Faults on Low Voltage Underground Cables. IET 9th International Conference on Developments in Power System Protection, 2008. DPSP 2008, 17-20 March 2008, Glasgow, 714-719.
- Pandey, A. and Younan, N.H. (2010) Underground Cable Fault Detection and Identification via Fourier Analysis. 2010 International Conference on High Voltage Engineering and Application (ICHVE), 11-14 October 2010, New Orleans, 618-621. http://dx.doi.org/10.1109/ICHVE.2010.5640779
- Long, Z.L., Younan, N.H. and Bialek, T.O. (2012) Underground Power Cable Fault Detection Using Complex Wavelet Analysis. 2012 International Conference on High Voltage Engineering and Application (ICHVE), 17-20 September 2012, Shanghai, 59-62. http://dx.doi.org/10.1109/ICHVE.2012.6357058
- Gilany, M., Ibrahim, D.K. and Eldin, E.S.T. (2007) Traveling-Wave-Based Fault-Location Scheme for Multiend-Aged Underground Cable System. IEEE Transactions on Power Delivery, 22, 82-89. http://dx.doi.org/10.1109/TPWRD.2006.881439
- Steennis, E.F. and Kreuger, F.H. (2002) Water Treeing in Polyethylene Cables. IEEE Transactions on Electrical Insulation, 25, 989-1028. http://dx.doi.org/10.1109/TPWRD.2006.881439
- Maeda, T., Kaneko, D., Ohki, Y., Konishi, T., Nakamichi, Y. and Okashita, M. (2004) Effect of the Applied Voltage Frequency on the Water Tree Shape in Polyethylene. Proceedings of the 2004 IEEE International Conference on Solid Dielectrics, 2004. ICSD 2004, 1, 276-279. http://dx.doi.org/10.1109/ICSD.2004.1350344
- Hwang, B.K. (1990) A New Water Tree Retardant XLPE. IEEE Transactions on Power Delivery, 5, 1617-1627. http://dx.doi.org/10.1109/61.58008
- Leslie, Y.Y., Dmitri, L., Shau-Chun, W. and Hsueh-Chia, C. (2004) A New AC Electrospray Mechanism by Maxwell-Wagner Polarization and Capillary Resonance. Physical Review Letters, 92, Article ID: 133902.
- Koo, J.Y., Cross, J.D., El-Kahel, M., Meyer, J.C. and Filippini, J.C. (1983) Annual Report of the Conference on Electrical Insulation and Dielectric Phenomena. 301.
- Filippini, J.C., Koo, J.Y. and Chen, J.L. (1989) Electrode Influence on the Propagation of Water Trees in Polyethylene. IEEE Transactions on Electrical Insulation, 24, 75-82. http://dx.doi.org/10.1109/14.19868
- Burkes, K., Makram, E.B. and Hadidi, R. (2014) Water Tree Detection in Underground Cables Using Time Domain Reflectometry. Department of Electrical and Computer Engineering, Clemson University, Clemson. (Unpublished)
- Burkes, K. (2014) Water Tree Analysis and On-Line Detection Algorithm Using Time Domain Reflectometry. Master’s Thesis, Clemson University, Clemson, 29634.
NOTES
*Corresponding author.














