Open Journal of Social Sciences
Vol.03 No.10(2015), Article ID:60213,7 pages
10.4236/jss.2015.310002
Analyzing the Operational Efficiency of Container Ports in Sub-Saharan Africa
Anguibi China Flora Carine
School of Economics and Management, Shanghai Maritime University, Shanghai, China
Email: anguibicarine@hotmail.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 1 September 2015; accepted 6 October 2015; published 12 October 2015
ABSTRACT
This study presents an evaluation of the relative efficiency of sixteen container ports in Sub-Sa- hara Africa using three DEA models namely CCR, BCC and Super-Efficiency over the year 2012. The CCR and BCC models are used to estimate the technical and scale efficiency while the super-effi- ciency technique provides a ranking of efficient ports. The efficiency results indicate that on average the inefficiency observed in the container ports under evaluation is due to scale rather than technical inefficiency. Further, by investigating the nature of the returns to scale, the study concludes that the majority of the container ports exhibit variable returns to scale while fewer experience constant returns to scale in their operations. In order to improve their overall efficiency, the ports showing increasing and decreasing returns to scale need to increase and decrease their size, respectively. Consequently, for container ports to survive in the competitive environment, port authorities should examine their operational scale to identify whether the production size is appropriate or not before making investment decision in terms of inputs resources enhancement or capacity expansion.
Keywords:
Container Ports, Efficiency, Nature of Returns to Scale, Data Envelopment Analysis, Sub-Saharan Africa

1. Introduction
Standing at the interface of sea and inland transportation, seaport represents major gateway for international trade in Sub-Saharan African (SSA) international trade. 90% of SSA total imports and exports volume is conducted by way of maritime transportation [1] . However, despite recent reforms and new investment made to increase the growth of throughput in many container terminals in Sub-Saharan Africa, many seaports on this part of the continent are by global standard the least productive in the world [2] . The ports suffer from lack of adequate facilities and investment, long delays and dwell time causing congestion affecting import prices and export competitiveness. In order to improve the possibilities of development of SSA ports in the competitive environment, it seems important to examine their relative performance to identify whether they are operating efficiently in the utilization of resources in terms of people, equipment and management process. Accordingly, this paper aims to analyze the relative efficiency of the ports in Sub-Saharan Africa.
Port efficiency evaluation is essential to both the economic theorist and the economic policy maker [3] . Previous research on efficiency studied the concept in terms of technical efficiency related to physical quantities as well as technical relationships and allocative efficiency considering profit and cost [4] . In the literature, the most common efficiency concept is technical efficiency [5] . Technical efficiency has been defined as the degree to which a given set of inputs are converted into output relative to the best practice on the efficiency frontier [4] . In other words, a firm is assumed to be technically efficient if that firm can produce maximum outputs from a given inputs without waste of resources when compared with its competitors. Moreover, scholar [4] suggested mea- suring technical efficiency as the ratio of output to input.
Efficiency measurement has been addressed in port sector by many researchers using two popular methodologies, that is, parametric approaches using econometric tools [6] - [8] and non-parametric approach based on mathematical programming theory [9] - [11] . In the past decades, the non-parametric model namely Data Envelopment Analysis has been given enormous attention in the assessment of efficiency in port sector [12] . Data Envelopment Analysis (DEA) is an efficiency evaluation model used to estimate the technical efficiency of decision making units (DMUs). In the literature pertaining to port efficiency, different DEA methods based on various combinations of inputs and outputs have been employed in many contexts. According to researchers [13] , the efficiency result obtained depend on the type of DEA model used, which in turn is based on an assumption made about the returns to scale properties of port production function as well as the input and output orientation approach.
For instance, a research conducted in China, using cross-sectional data, examined the technical efficiency of 42 container terminals [14] . The researchers applied CCR (Charnes, Cooper, and Rhodes) and BCC (Banker, Charnes, Cooper) DEA models developed by scholars [15] and [16] respectively, as estimation methods. The CCR model provided an aggregate measure of pure technical efficiency calculated through BCC model and scale efficiency. Pure technical efficiency is related to the ability of DMUs in utilizing their resources while scale efficiency represents the degree to which the size of a DMU diverges from optimal scale. In other words, a particular DMU is scale efficient when its operational scale is optimal, indicating that any changes (an increase or decrease) in its size will reduce its efficiency. Researchers [14] found that inefficiency of the coastal container terminals was mainly due to scale inefficiency, that is, on average the production size was not appropriate regarding the activities performed by the ports. The findings also showed an excessive waste in resources utilization in the Chinese container terminals. A similar national level study on the basis of one time period data has evaluated port efficiency in Vietnamese context using DEA approach [17] . The outcome revealed useful information on the ability of the Vietnamese ports in managing their inputs resources to get the desired output. Besides, Stochastic Frontier Analysis (SFA) has also been applied to calculate the efficiency. Comparing the results of the models, the scholars found that the estimations derived from both techniques were significant but different due to their underlying assumptions. In another study performed in Asian region, CCR and BCC techniques have been used to identify the source of inefficiency in the sample ports. The outcome showed that the overall technical inefficiency observed was related to technical rather than scale inefficiency [18] . Further, past study conducted in Northeast Asia, applying three types of DEA especially CCR, BCC and Super-efficiency, demonstrated that Hong Kong was the most efficient port in the Northeast Asia, relative to the efficient frontier [19] . Investigating the operational efficiency of the world’s major container ports, researchers [20] applied DEA models based on constant and variable returns to scale assumptions to determine the source of inefficiency and areas of improvement for the inefficient ports. Moreover, comparing the efficiency of four Australian and twelve other international container ports using DEA technique, scholar [21] found that the ports of Melbourne, Rotterdam, Yokohama and Osaka were the most inefficient in the sample. The researcher indicated that the inefficiency in the sample ports was a result to the waste of inputs such as container berths, terminal area and labor. Similarly, a study investigating the efficiency of 86 ports across the world highlighted that the most inefficient ports had used excessively their resources [22] , meaning that there was a waste of inputs in the production process.
Since the introduction of DEA model in port efficiency evaluation by researchers [9] , many studies have extended the sample data from cross-sectional to panel data in order to identify the possibility of change in port efficiency over time. The change in efficiency has been studied using the DEA method in Latin American Container seaports [23] . The analysis revealed an improvement of the pure technical efficiency of the Latin American seaports over the period 2000 to 2008. In the same way, a research applying DEA method for the period of 2001 to 2010 in Nigeria, demonstrated a continuous enhancement of the efficiency of Onne and Rivers seaports since the year 2006 [24] . In Malaysia, DEA-window analysis based on panel data from 2003 to 2010 has been applied to evaluate the efficiency of six major container ports [25] . Terminal equipment and container throughput have been selected respectively as input and output. The researcher concluded that the cause of inefficiency was due to technical rather than scale efficiency during the period under evaluation. Similarly, Middle Eastern and East African Seaports have been compared using standard DEA and DEA-window models [26] . The outcome highlighted a similarity in average efficiency values obtained from the cross-sectional data and the panel data. In addition, among the African ports selected in the study, Mombasa and Djibouti have experienced an improvement during the period. Conversely, analyzing the technical efficiency of African seaports using a bootstrapped DEA, Nigerian seaports have been found as the most efficient, followed by Mozambique and Angola [27] . According to the researchers, ports efficiency could be affected by the political situation experienced by each country as well as national infrastructure plan.
Based on the literature, we conclude that DEA models have been widely used to determine among similar ports, the efficient DMUs and identify areas of improvement for the inefficient ones. In addition, it is identified that various combinations of inputs and outputs have provided different efficiency results. However, a research investigating the operational efficiency of Sub-Saharan Africa container ports has not been found in the literature. Therefore, this study attempt to examine the efficiency of sixteen ports in Sub-Saharan Africa using three types of DEA models. The remainder of this study is organized in following ways. The data source and DEA models are introduced in Section 2. Section 3 presents and discusses the results of empirical study conducted on the sixteen containers ports and we conclude our study in Section 4.
2. Data and Methodology
2.1. Data and Specification of Variables
This paper selected major container ports in Sub-Saharan Africa. In order to be consistent with the production function framework, proxies have been used to estimate labor and capital inputs in previous studies applying DEA technique to evaluate the efficiency of ports. For instance, handling equipment has been measured as a proxy for labor input; terminal area and quay length have been selected as a proxy for capital [18] . In addition, researcher [21] emphasized the absence of consensus in the choice of inputs and outputs variables. Hence, this paper uses the number of quayside crane and yard equipment as a proxy of labor. On the other hand, terminal area and quay length are considered as a proxy of capital and container throughput is used as the only output. The data was obtained from official websites of the container ports and their related port authorities association for the year 2012.
2.2. Methodology Adopted
Data envelopment analysis is a non-parametric method for estimating the relative performance of decision making units (DMUs). The DEA technique requires no assumption related to the nature of the relation between the inputs and the outputs and can handle multiple inputs and multiple outputs in the computation of efficiency values [28] . Besides, in the absence of precise information on the nature of returns to scale, it is suggested to apply both DEA models [21] . Consequently, to assess the technical and scale efficiency of the container ports, the study applied CCR and BCC assuming constant returns to scale and variable returns to scale, respectively. Based on the previous work on efficiency measurement [4] , researchers [15] developed the CCR model. Considering that efficiency can be measured as the ratio of outputs to inputs, scholars [15] proposed the following mathematical programming problem for estimating the relative efficiency score of a particular DMU j among similar n entities being evaluated:
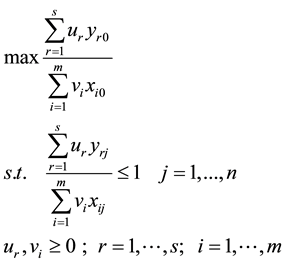 (1)
(1)
where 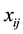 is the amount of inputs i used to obtain
is the amount of inputs i used to obtain  the amount of output r produced by DMU j.
the amount of output r produced by DMU j. 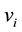 and
and  are the weight assigned to input i and output r respectively.
are the weight assigned to input i and output r respectively.
To solve the fractional mathematical programming problem, Equation (1) has been transformed into a linear programming model (primal formal) written below:
 (2)
(2)
To obtain the solution of Equation (2), the dual form has been considered and presented as follow:
 (3)
(3)
The CCR model given above follows an input-oriented approach that is the minimization of resources for a desired amount of outputs. The present study adopted an output-oriented approach in order to determine how a port could efficiently increase its throughput from a particular quantity of resources. Similar to the input- oriented CCR model formulation, the output-oriented CCR dual form is shown as follows:
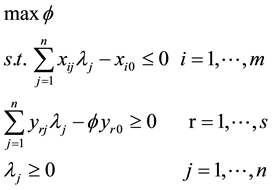 (4)
(4)
where  is the value of the relative efficiency score for each DMU being evaluated.
is the value of the relative efficiency score for each DMU being evaluated.
By assuming that not all the decision making units are operating at an optimal scale, the constraint presented below is added to the CCR also called constant return to scale (CRS) model, to obtain the BCC known as variable returns to scale (VRS) model introduced by [16] .
 (5)
(5)
The inverse of the estimated score of 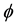 gives the efficiency value for each DMU in both CCR and BCC model. A DMU is considered as efficient in both models when its efficiency score is equal to one. In case, the efficiency value is less than one the DMU is inefficient.
gives the efficiency value for each DMU in both CCR and BCC model. A DMU is considered as efficient in both models when its efficiency score is equal to one. In case, the efficiency value is less than one the DMU is inefficient.
Analyzing the efficiency of the DMUs under VRS assumptions, the scale efficiency (SE) of each DMU has been estimated using the efficiency scores obtained under CCR and BCC models. In fact, the efficiency observed under the CRS model is the overall measure of technical and scale efficiency (TE) while the one deriving from the VRS model is pure technical efficiency (PTE). Hence, scale efficiency is calculated as follows:
 (6)
(6)
where SE equal to 1 indicates scale efficiency and less than one demonstrates scale inefficiency.
After estimation of scale efficiency, the nature of returns to scale has been investigated to determine whether the scale inefficiency is related to either increasing (IRS) or decreasing returns to scale (DRS). In order to find the nature of returns to scale, a comparison is made between the efficiency value given by BCC model and the one calculated under non increasing returns to scale (NIRS) model. According to researchers [29] , if the efficiency value of NIRS model is different to the BCC efficiency score, thus the DMU being assessed exhibit increasing returns to scale. In case, both efficiency indices are equal, then the particular DMU experiences decreasing returns to scale. The NIRS model is obtained by adding the restriction written below instead of the constraint displayed in Equation (5) in the CCR model in Equation (4).
 (7)
(7)
As mentioned above, the standard DEA models CCR and BCC give the same efficiency value of one to all the efficient DMU. Consequently, it is not possible to identify among the efficient DMUs, the best performer. In order to provide ranking among only the efficient ports, the super-efficiency model developed by [30] has been applied. The Super efficiency model formulation is similar to the above mentioned models. However, it excludes the decision making unit being estimated from the reference set and gives a value equal or greater of one to the efficient DMUs, assuming for instance that, the best efficient DMU has a higher score.
3. Empirical Results
The characteristics of the variables used to estimate the relative efficiency of the sample ports are presented in Table 1.
The study used CCR and BCC DEA models under the assumption of output maximization to estimate the overall technical efficiency, pure technical efficiency, scale efficiency and the nature of returns to scale for sixteen container ports. On the other hand, Super-efficiency model which extend the standard DEA models by providing a ranking of the efficient decision making unit based on its super-efficiency scores has been employed as well. The results are summarized in Table 2.
The efficiency estimates of the CCR model of Mombasa, Tema, Lagos, Douala and Luanda are equal to one, revealing that these ports define the best practice frontier. The efficiency scores of the remaining ports are less than one, demonstrating that they are relatively inefficient compared with the efficient ports on the best practice frontier. Considering the efficiency scores derived from BCC model, it is found that, in addition to, the efficient ports identified under the CCR model, Lome, Cotonou, Cape Town, Libreville and Maputo have their efficiency
Table 1. Descriptive statistics for inputs and outputs variables derived from CCR model.
Table 2. Efficency results derived from DEA methods.
score equal to one, indicating that they are efficient in terms of resource utilization. Therefore, among the sixteen ports under evaluation, five are efficient in constant returns to scale model whereas ten are operating efficiently under variable returns to scale model.
Analyzing the source of inefficiency, the overall technical efficiency has been decomposed into pure technical efficiency and scale efficiency in order to determine whether the inefficiency is a consequence of an inefficient utilization of input or an inappropriate production scale or size. Under the assumption of VRS, the average technical efficiency score is 92.2%, suggesting that on average using the same amount of inputs, the ports outputs can be increase by 7.8%. The average efficiency value obtained from the CRS model is 78.3%, which is less than the average efficiency score estimated in VRS model. The average scale efficiency score (value = 85.5%) indicates that on average the ports actual scale of production has deviated from the most productive scale size (MPSS) by 14.5%. On the whole, the results reveal that the source of the overall inefficiency is due to scale rather than pure technical inefficiency. The ports of Mombasa, Tema, Lagos, Douala and Luanda are scale and technically efficient with a score of one. Hence, the ports were operating at the optimal scale. Conversely, Lome, Cotonou, Cape Town, Libreville and Maputo of which the efficiency scores is less than 1 in CCR model, are efficient under BCC model, demonstrating that they are technically efficient but scale inefficient. In other words, the ports were efficient in the utilization of input resources but they are either too small or too large regarding the activities they perform. The remaining ports are both scale and technically inefficient. Therefore, the inefficient ports have to adjust their scale of operations in order to move towards the efficient frontier.
The results derived from the analysis of the nature of returns to scale are summarized in the right-most column of Table 2. The outcome highlighted that five efficient ports exhibit constant returns to scale. In addition, three ports are operating at decreasing returns to scale, revealing that their size is too large regarding the activities performed. As a result, these ports need to reduce their operational scale. However, the remaining ports showing increasing returns to scale due to their small size of production need to enhance their efficiency by selecting a scaling up strategy that is increasing their scale of operations.
As emphasized above, the standard CCR and BCC models classify the decision making unit into best performers and inefficient units but cannot determine the relative ranking of the efficient DMUs. Hence, this study adopted the super-efficiency model to rank the efficient performers in the sample ports. The results indicate that Mombasa has the best performance with a score of 1.434, followed by Tema (score = 1.266), Lagos (score = 1.221), Luanda (score = 1.170) and Douala (score = 1.111). The difference observed in the efficiency scores illustrates that with the same scale, Mombasa port has better management practices compared with the other ports. Conversely, as the efficiency values of the inefficient ports are the same in both the super-efficiency and CCR model, Maputo is considered as the most inefficient with a value of 0.304.
4. Conclusions
This paper evaluates the relative efficiency of sixteen container ports in Sub-Saharan Africa using three DEA models namely CCR, BCC and Super-Efficiency over the year 2012. The DEA technique was performed based on output-oriented approach.
The efficiency scores obtained in CCR and BCC models reveal that 31.25% of the ports are relatively efficient and experience constant returns to scale while the other ports (68.75%) are operating under variable returns to scale. Further, the analysis of the nature of returns to scale indicates that about 18.75% of the ports exhibit decreasing returns to scale while 50% shows increasing returns to scale. It is suggested that the ports observed in the decreasing returns to scale zone should reduce their scale of operation whereas the others ports showing increasing returns to scale should increase their production scale. On the whole, the inefficient ports being assessed suffer from the effect of inappropriate operational scale. Consequently, for container ports to survive in the competitive environment, port authorities should examine their operational scale to identify whether the production size is appropriate or not before making investment decision in terms of inputs resources enhancement or capacity expansion. Finally, the results given by super-efficiency indicate that among the sample ports Mombasa has the best management practices while Maputo is the most inefficient one suffering from scale inefficiency.
In the case of this research, the inefficiency of Abidjan, one of the major ports in West Africa, could be related to the political crisis in Ivory Coast (2010-2011). In fact, the crisis has caused a decline in the numbers of ship call which resulted in the decrease of the throughput. Thus, as pointed out by researchers [27] , port inefficiency can be related to political instability. Accordingly, we recommend using panel data to investigate the efficiency trends of the sample ports. In addition, for enhancing their operational performance, Sub-Saharan Africa ports need a national infrastructure strategy to promote public-private investment in the sector in order to raise adequate capital and acquire the new technology and process.
Cite this paper
Anguibi China FloraCarine, (2015) Analyzing the Operational Efficiency of Container Ports in Sub-Saharan Africa. Open Journal of Social Sciences,03,10-17. doi: 10.4236/jss.2015.310002
References
- 1. Raballand, G., Refas, S., Beuran, M. and Isik, G. (2012) Why Does Cargo Spend Weeks in Sub-Saharan African Ports?: Lessons from Six Countries. World Bank Publications, Washington DC. http://dx.doi.org/10.1596/978-0-8213-9499-1
- 2. United States International Trade Commission (2009) Sub-Saharan Africa: Effects of Infrastructure Conditions on Export Competitiveness, Third Annual Report. US International Trade Commission, Washington DC.
- 3. Wang, T.F., Song, D.W. and Cullinane, K. (2002) The Applicability of Data Envelopment Analysis to Efficiency Measurement of Container Ports. Proceedings of the International Association of Maritime Economists Conference, Panama, 13-15 November 2002, 13-15.
- 4. Farrell, M.J. (1957) The Measurement of Productive Efficiency. Journal of the Royal Statistical Society. Series A (General), 120, 253-290. http://dx.doi.org/10.2307/2343100
- 5. Porcelli, F. (2009) Measurement of Technical Efficiency. A Brief Survey on Parametric and Non-Parametric Techniques. http://www.warwick.ac.uk/fac/soc/economics/staff/phd_students/porcelli/porcelli_dea_sfm.pdf.
- 6. Cullinane, K. and Song, D.W. (2003) A Stochastic Frontier Model of the Productive Efficiency of Korean Container Terminals. Applied Economics, 35, 251-267. http://dx.doi.org/10.1080/00036840210139355
- 7. Wang, T.F. and Cullinane, K. (2006) The Efficiency of European Container Terminals and Implications for Supply Chain Management. Maritime Economics & Logistics, 8, 82-99. http://dx.doi.org/10.1057/palgrave.mel.9100151
- 8. Cullinane, K. and Song, D.W. (2006) Estimating the Relative Efficiency of European Container Ports: A Stochastic Frontier Analysis. Research in Transportation Economics, 16, 85-115. http://dx.doi.org/10.1016/S0739-8859(06)16005-9
- 9. Roll, Y. and Hayuth, Y. (1993) Port Performance Comparison Applying Data Envelopment Analysis (DEA). Maritime Policy and Management, 20, 153-161. http://dx.doi.org/10.1080/03088839300000025
- 10. Pjevcevic, D., Radonjic, A., Hrle, Z. and Colic, V. (2012) DEA Window Analysis for Measuring Port Efficiencies in Serbia. PROMET-Traffic & Transportation, 24, 63-72. http://dx.doi.org/10.7307/ptt.v24i1.269
- 11. Bo, L.U. and Wang, X.L. (2012) Comparative Studies on Efficiency Evaluation of Chinese and Korean Major Container Terminals. Advances in Information Sciences & Service Sciences, 4, 434-442.
- 12. González, M.M. and Trujillo, L. (2009) Efficiency Measurement in the Port Industry: A Survey of the Empirical Evidence. Journal of Transport Economics and Policy (JTEP), 43, 157-192.
- 13. Poitras, G., Tongzon, J. and Li, H. (1996) Measuring Port Efficiency: An Application of Data Envelopment Analysis. Singapur, Department of Economics and Statistics, National University of Singapore, Singapore.
- 14. Dan, L.I., Weixin, L.U.A.N. and Feng, P.I.A.N. (2013) The Efficiency Measurement of Coastal Container Terminals in China. Journal of Transportation Systems Engineering and Information Technology, 13, 10-15. http://dx.doi.org/10.1016/S1570-6672(13)60121-X
- 15. Charnes, A., Cooper, W.W. and Rhodes, E. (1978) Measuring the Efficiency of Decision Making Units. European Journal of Operational Research, 2, 429-444. http://dx.doi.org/10.1016/0377-2217(78)90138-8
- 16. Banker, R.D., Charnes, A. and Cooper, W.W. (1984) Some Models for Estimating Technical and Scale Inefficiencies in Data Envelopment Analysis. Management Science, 30, 1078-1092. http://dx.doi.org/10.1287/mnsc.30.9.1078
- 17. Nguyen, H.O., Nguyen, H.V. and Chin, A.T.H. (2011) Efficiency Measurement Using the Stochastic Frontier Analysis and Data Envelopment Analysis Methods: An Application to the Vietnamese Ports. Singapore Economic Review Conference 2011, Singapore, 4-6 August 2011, 1-13.
- 18. Munisamy, S. and Singh, G. (2011) Benchmarking the Efficiency of Asian Container Ports. African Journal of Business Management, 5, 1397-1407.
- 19. So, S., Kim, J., Cho, G. and Kim, D.K. (2007) Efficiency Analysis and Ranking of Major Container Ports in Northeast Asia: An Application of Data Envelopment Analysis. International Review of Business Research Papers, 3, 486-503.
- 20. Lu, B., Park, N.K. and Huo, Y. (2015) The Evaluation of Operational Efficiency of the World’s Leading Container Seaports. Journal of Coastal Research, 73, 248-254. http://dx.doi.org/10.2112/SI73-044.1
- 21. Tongzon, J. (2001) Efficiency Measurement of Selected Australian and Other International Ports Using Data Envelopment Analysis. Transportation Research Part A: Policy and Practice, 35, 107-122. http://dx.doi.org/10.1016/S0965-8564(99)00049-X
- 22. Herrera, S. and Pang, G. (2008) Efficiency of Infrastructure: The Case of Container Ports. Revista de Economia, 9, 165-194.
- 23. Munisamy, S. and Jun, O.B. (2013) Efficiency of Latin American Container Seaports Using DEA. Proceedings of 3rd Asia-Pacific Business Research Conference, Kuala Lumpur, 25-26 February 2013, 25-26.
- 24. Okeudo, G.N. (2013) Measurement of Efficiency Level in Nigerian Seaport after Reform Policy Implementation. Case Study of Onne and Rivers Seaport, Nigeria. IOSR Journal of Business and Management (IOSR-JBM), 12, 46-55. http://dx.doi.org/10.9790/487X-1254655
- 25. Mokhtar, K. (2013) Technical Efficiency of Container Terminal Operations: A DEA Approach. Journal of Operations and Supply Chain Management, 6, 1-19. http://dx.doi.org/10.12660/joscmv6n2p1-19
- 26. Al-Eraqi, A.S., Mustafa, A., Khader, A.T. and Barros, C.P. (2008) Efficiency of Middle Eastern and East African Seaports: Application of DEA Using Window Analysis. European Journal of Scientific Research, 23, 597-612.
- 27. Barros, C.P., Assaf, A. and Ibiwoye, A. (2010) Bootstrapped Technical Efficiency of African Seaports. In: Coto-Millán, P., Pesquera, M.A. and Castanedo, J., Eds., Essays on Port Economics, Physica-Verlag HD, Heidelberg, 237-250. http://dx.doi.org/10.1007/978-3-7908-2425-4_15
- 28. Cooper, W.W., Seiford, L.M. and Zhu, J. (2011) Data Envelopment Analysis: History, Models, and Interpretations. In: Cooper, W.W., Seiford, L.M. and Zhu, J., Eds., Handbook on Data Envelopment Analysis, Springer US, New York, 1-39. http://dx.doi.org/10.1007/978-1-4419-6151-8_1
- 29. Banker, R.D., Cooper, W.W., Seiford, L.M., Thrall, R.M. and Zhu, J. (2004) Returns to Scale in Different DEA Models. European Journal of Operational Research, 154, 345-362. http://dx.doi.org/10.1016/S0377-2217(03)00174-7
- 30. Andersen, P. and Petersen, N.C. (1993) A Procedure for Ranking Efficient Units in Data Envelopment Analysis. Management Science, 39, 1261-1264. http://dx.doi.org/10.1287/mnsc.39.10.1261


