Journal of Materials Science and Chemical Engineering
Vol.05 No.08(2017), Article ID:78478,15 pages
10.4236/msce.2017.58005
Gas Purification and Quality Control of the End Gas Product
Konstantin Chuntonov1*, Alexey O. Ivanov2, Boris Verbitsky1, Victor L. Kozhevnikov3
1Mechemlab Ltd., Nesher, Israel
2Institute of Mathematics and Computer Sciences, Ural Federal University, Yekaterinburg, Russia
3Institute of Solid State Chemistry, Russian Academy of Sciences, Yekaterinburg, Russia

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: July 19, 2017; Accepted: August 13, 2017; Published: August 16, 2017
ABSTRACT
One of the main problems in the flow-through gas purification technologies is related with continuous control of the outlet gas purity. The information concerning purity of the produced gas is on high demand, e.g., for processing systems integrated with gas purifiers. The positive solution of this problem has become possible only now due to the appearance of reactive getters (reactants) that serve as highly efficient sinks for gas impurities and our sorption model of the processes, which take place in gas purifiers with these reactants. According to the given model the appearance of a single valued functional connection between the purity of the gas product and the duration of the treatment of the gas flow by the sorbing powder is typical for any system Me -Y, where Me is a powder reactant and Y is an impurity gas. This strict correlation provides the mathematical justification to a simple method of determining the concentration of the impurity in the gas flow at the exit from the gas purifier. This method comes down to measuring of the quantity of the purified gas by a gas flow meter, the readings of which are graduated in the units of gas concentration.
Keywords:
Gas Purifier, Reactants, Sorption Model, Quality Control, Purity Indicator

1. Introduction
In the production of high purity gases an important place belongs to gas purifiers, which in the essence are flow-through tubes by themselves with a sink for capturing impurities from the treated gas. The molecular sieves or getter materials are commonly used for this purpose in powder form or in the form of sintered porous bodies [1] [2] [3] . The weak points of today’s purification methods include low sorption capacity and quality control of the end gas product. The practically achieved sorption capacity of the traditional getter materials is rather low at room temperature [4] [5] . The situation is no better with the purity control where the cost of the precision analytical equipment and measurements by many times exceed the cost of gas purifiers and gas production.
Therefore, the progress in this field can be feasible only with drastic impro- vements in the capturing capacity of getters and simplification of the methods for continuous control of impurities in the outlet gas.
The main step in the indicated direction is the development of getters with sorption capacity much larger compared to similar materials on the basis of transition metals [6] [7] . In order to approach the other side of the problem, i.e. purity control, it is worth noticing that for many users of high purity gases it is not particularly important to know exactly the amount of impurities. More vital thing is to have confidence that the impurities content is within the range of the required purity.
The aim of the present paper is to describe the impurity gas capturing with a powder reactant in the flow-through gas purifier. The theory of the process is further used for searching the methods allowing replacing of costly direct measurements with inexpensive indirect ones.
2. Problem Statement
The dynamic sorption of gases by adsorbents is well studied [8] [9] [10] [11] . This cannot be said about gas capturing by reactants (under reactants we will further understand alkali or alkali-earth metals or their alloys [12] ). Unlike adsorbents, reactants (henceforth Me) provide the entire volume of the material for capturing gas Y by forming a non-volatile chemical compound MeY (Figure 1).
While the surface of adsorbents rapidly passivates in gas medium and gas sorption by absorbents is limited at room temperature by diffusion and low values of the ultimate solubility of gases in solids, reactants continuously capture gases till the material is entirely exhausted in the chemical reaction. At the limit sorption capacity of reactants is determined by the ratio Me:Y = 1:1, i.e. for capturing of one gas atom one metal atom is “spent”, which is unique for such application field as gas purification.
The difference between adsorbents and reactants is also significant in respect to the sorption kinetics. At initial stages, when active surface sites are abundant, adsorbents and reactants are similar in their activity. However, the saturation of the surface with impurity adatoms results in practical termination of the sorption process while in the case of reactants it is accompanied only with a change in the intake mechanism. The quantity m of the captured impurity Y at constant concentration in the gas phase may change with time either as 
Figure 1. Three getter classes: adsorbents, absorbents and reactants. Me―metal, Y―gas, MeY―chemical compound, [Y]Me―solid solution of Y in Me;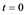 , fresh surface of Me,
, fresh surface of Me, 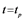 , passivation time of the adsorbent;
, passivation time of the adsorbent;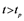 , solubilizing or formation of the com- pounds in the case of absorbents and reactants,
, solubilizing or formation of the com- pounds in the case of absorbents and reactants,  , the state of equilibrium between absorbents and reactants with gas Y.
, the state of equilibrium between absorbents and reactants with gas Y.
or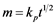 , where
, where 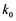 and
and 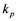 are kinetic constants depending on the reactant nature.
are kinetic constants depending on the reactant nature.
Now we can start solving the problem of gas purification in a flow-through tube with the powder reactant Me. Let’s consider an elementary layer dx containing n particles of the reactant limited by coordinates x1 and 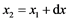 along the tube of the length L and radius R. We suppose that the reactant particles are spheres with radius r0, and the porosity coefficient of the powder mass is ε. Then the layer volume
along the tube of the length L and radius R. We suppose that the reactant particles are spheres with radius r0, and the porosity coefficient of the powder mass is ε. Then the layer volume 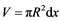 can be presented as a sum
can be presented as a sum , where
, where 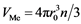 is the volume of the reactant and
is the volume of the reactant and 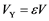 is the volume of voids within the layer, Figure 2.
is the volume of voids within the layer, Figure 2.
Hence, we find that 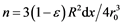 and the total surface of the reactant particles in the elementary layer is
and the total surface of the reactant particles in the elementary layer is .
.
The gas enters the layer with the impurity concentration 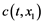 and leaves it with a smaller concentration
and leaves it with a smaller concentration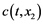 . The decrease in the concentration is due to the intake of the impurity by the reactant Me. Let’s define the concen- tration of the impurity in Me as
. The decrease in the concentration is due to the intake of the impurity by the reactant Me. Let’s define the concen- tration of the impurity in Me as



The material balance for the sink of impurities is

where 


Figure 2. Elementary layer of powder mix in a flow tube.
Me. The right hand part 
Let us assume that we deal with a linear sorption law and a chemical reaction of first order. Then the increment of the amount of gas Y that sank in the layer 



where 
The value

where 



Here, 



Equation (4) is to be supplemented with the obvious boundary conditions


3. The Model
Let us introduce dimensionless parameters:







In this case the mathematical model is transformed to the form:



where

is a functional of the dimensionless concentration
The solution of the problem (7)-(10) was found with the help of an iterative method (see Appendix II). The problem has two controlling parameters: A and B, where A determines the rate of the impurity intake from the gas and B determines the lifespan of the powder reactant. At the stage of the analysis an issue of the time scale of the discussed process arises. As it follows from the model (7)-(10) the solution at the first iteration (formula II.1, Appendix II) describes the steady-state impurity concentration distribution in the conditions of “inexhaustible sink” when function




The calculated time dependent changes for the gas concentration are pre- sented in Figure 3, where curve 
Particularly illustrative is the curve







The plots in Figure 4 illustrate the convergence of the results in the adopted iterative calculation procedure.
Figure 3. Distribution of gas concentration along the tube at different values of τ. u1―the first iteration, u2―the second iteration; the initial data: A = 5, B = 10−1.
Figure 4. Concentration profile of the gas flow of the tube in three interations. 1, 2 and 3―the first, the second and the third iterations accordingly; the initial data: A = 5, B = 10−1.
In fact, it can be seen that curve u3 is clearly closer to curve u2 than the latter is to curve u1. Let us also have in mind that qualitative behavior of curves repeats for all the iterations. That is, there are all the reasons to believe that the presented here approximation is correct and can be used for searching for correlations between the purity of the end gas product and one or another measurable parameter of the sorption process.
The question about the dependence of concentration Y in the flow of gas in the outlet from the gas purifier on time is the question about the behavior of function
The plot for 

As regards the degree of purification of the gas flow, its maximal value according to Appendix II is limited by
Figure 5. Dependence of the purity of gas product on time τ. The initial data: A = 10, B = 2 × 10−6.
the first portions of purified by the reactant gas will have the purity of about 99.9999995%.
For better understanding let us go back to 
In the given figure a chain of situated along axis 

4. Discussion
Function 

Figure 6. Structural―phase evolution of the sorbent particles and concentration of gas impurity. (a) Dependence of gas concentration on ξ at τ = 10 according to the second iteration; (b) The phase structure of the sorbent particles: light areas―Me, dark areas―MeY; the initial data: A = 5, B = 10−1.
under the condition that the characteristics of the system Me-Y as well as the technical data of the equipment and the process parameters retain their values with time, curve 
The total amount of gas that passed through the tube at time τ is 





where 

Then the share of the reactant spent at time τ and coordinate 

while the total share of the reactant that has entered into reaction with impurity Y at time τ (see Figure 6) is

The graphical form of this function (D(τ) henceforth) is given in Figure 7.
On the other hand, the same share D(τ) can be expressed as


Substituting (12) in (11) we finally arrive to dependence of the purity of outlet gas on τ

where 
Formulas (12) and (13) are the contribution of the sorption theory of reactants, which we are developing, in the technology of gas purification. Formula (12) allows estimating in the efficiency of purification according to the cost/quality criterion. For this it is enough to assume in (12) 

and to repeat these estimations, if required, for other purity levels uc of the end product.
Figure 7. Change of share D of sorption waste with time. 1, 2 and 3―the first, the second and the third iterations accordingly; the initial data: A =10, B = 2 × 10−6.
In its turn formula (13) can be considered as a theoretical grounding of the
method of determination of the purity of the outlet gas according to purification time. At engineering level this method is realized by using a timer with a display graduated according to the results of the analysis of the gas samples taken in specified time intervals at the outlet of the flow tube. This supposes organization of a preliminary testing procedure with the involvement of precision analytical equipment according to the data of which experimental curve 

In industrial conditions it is more convenient to use not 
If in expression for N we pass over from τ to real time 





In this case in much the same way as an experimental curve 



The reliability of such an indicator will be very high if in its graduating the results of several tests performed with the help of Atmospheric Pressure Chemical Ionization Mass Spectrometer (APCI-MS) are used. The existing gas analyzers for gas stream monitoring are capable of detecting only a very limited set of gas species. For this reason the indicator, which we are describing here, should be tuned for determining the concentration of the main, i.e. the target gas and in this case the APCI-MS is indispensable.
So, the analysis of the sorption phenomena in powder reactants shows the possibility of solving the problem of economical security of the process systems, which use in their technologies gases fed from gas purifiers. The authors realize the importance of this problem for gas industry and are planning to describe in their next publication how the idea of the indicator of purity of the gas product is modifies depending on the conditions of the sorption process. What is understood here is the substitution in gas purifiers the reactants following the linear sorption law with the reactants following parabolic law as well as the transfer from the sorption processes in motionless powders to the processes with the participation of tribological effects.
5. Conclusions
1) A mathematical model is developed for the process impurity gas capturing by powder reactants in flow tubes targeted for finishing gas purification.
2) The solutions of the model show the existence of the single valued functional connection 
3) The mentioned function provides the theoretical basis for the attempts of creating indirect methods of measuring purity of the gas product.
4) Any attempt of this kind by necessity includes certain practical actions aimed at building experimental curves 



5) The simplest variant of this kind of an indicator is a gas flow meter calibrated for the units of gas concentration.
On the whole, it can be expected that the appearance of gas purifiers with metallic reactants and purity indicators of the outlet gas will considerably improve the efficiency of gas purification and the level of economical security for the customers of high purity gases.
Acknowledgements
A. O. Ivanov gratefully acknowledges research funding from the Ministry of Education and Science of the Russian Federation [Contract no. 02.A03.21.0006, Project no. 3.1438.2017/4.6].
Cite this paper
Chuntonov, K., Ivanov, A.O., Verbitsky, B. and Kozhevnikov, V.L. (2017) Gas Purification and Quality Control of the End Gas Product. Journal of Materials Science and Chemical Engineering, 5, 44-58. https://doi.org/10.4236/msce.2017.58005
References
- 1. Zeller, R. and Vroman, C. (2006) Porous Sintered Composite Materials. US Patent No. 7112237.
- 2. Kerry, F.G. (2007) Industrial Gas Handbook: Gas Separation and Purification. CRC Press, Taylor & Francis Group, New York.
- 3. Rouquerol, J., Rouquerol, F., Llewellyn, P., Maurin, G. and Sing, K.S.W. (2013) Adsorption by Powders and Porous Solids: Principle, Methodology and Applications. 2 nd Edition, Academic Press, New York.
- 4. Chuntonov, K.A. and Yatsenko, S.P. (2013) Getter Films for Small Vacuum Chambers. Recent Patents on Materials Science, 6, 29-39.
https://doi.org/10.2174/1874464811306010029 - 5. Chuntonov, K., Setina, J. and Douglass, G. (2015) The Newest Getter Technologies: Materials, Processes, Equipment. Journal of Material Science and Chemical Engineering, 3, 57-67.
https://doi.org/10.4236/msce.2015.39008 - 6. Chuntonov, K. and Setina, J. (2016) Reactive Getters for MEMS Applications. Vacuum, 123, 42-48.
https://doi.org/10.1016/j.vacuum.2015.10.012 - 7. Chuntonov, K. and Setina, J. (2017) Activationless Gas Purifiers with High Sorption Ca-pacity. US Patent No. 9586173.
- 8. Adamson, A.W. (1982) Physical Chemistry of Surfaces. 4th Edition, John Wiley & Sons, New York.
- 9. Masel, R.L. (1996) Principles of Adsorption and Reaction on Solid Surfaces. John Wiley & Sons, New York.
- 10. Toth, J. (2002) Adsorption: Theory, Modeling, and Analysis (Surfactant Science Series, Volume 107), Marcel Dekker, New York.
- 11. Yang, R.T. (2003) Adsorbents: Fundamentals and Applications. John Wiley & Sons, Hoboken.
https://doi.org/10.1002/047144409X - 12. Chuntonov, K., Atlas, A., Setina, J. and Douglass, G. (2016) Getters: From Classification to Materials Design. Journal of Materials Science and Chemical Engineering, 4, 23-34.
https://doi.org/10.4236/msce.2016.43004
Appendix I
The current radius 



The consumption of the metal Me in an act like this one is measured by a layer of thickness 


If the reactant has a shape of a ball particle of radius r (Figure 8(c)) then during time 



Basing on the above said and taking into account the data of Figure 8 we get that

where 

taking into consideration that 
One more remark. The thickness of the layer 

Figure 8. Linear sorption law. (a) and (b) flat material surface; (с) spherical body.
Figure 9. Movement of front Ξ as a function of time. Ξ1―the first iteration, Ξ2―the second iteration; the initial data: A = 5, B = 10−1.
process is accompanied with volume contraction of the product. The given fact together with the equality 
Appendix II
Equation (7) with boundary conditions (8) and (9) can be solved with the help of an iterative procedure, which in the essence is building up disturbances accord- ing to the small value of parameter B.
The first iteration gives
with the solution

The second iteration
results in the solution

Here 

The third iteration is so bulky that it is presented only in a graphical form.
Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/
Or contact msce@scirp.org
















