Journal of Materials Science and Chemical Engineering
Vol.04 No.07(2016), Article ID:69055,7 pages
10.4236/msce.2016.47011
Artificial Neural Network Model for Friction Factor Prediction
Uchechukwu Herbert Offor, Sunday Boladale Alabi
Department of Chemical and Petroleum Engineering, University of Uyo, Uyo, Nigeria

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 28 June 2016; accepted 9 July 2016; published 26 July 2016
ABSTRACT
Friction factor estimation is essential in fluid flow in pipes calculations. The Colebrook equation, which is a referential standard for its estimation, is implicit in friction factor, f. This implies that f can only be obtained via iterative solution. Sequel to this, explicit approximations of the Colebrook equation developed using analytical approaches have been proposed. A shift in paradigm is the application of artificial intelligence in the area of fluid flow. The use of artificial neural network, an artificial intelligence technique for prediction of friction factor was investigated in this study. The network having a 2-30-30-1 topology was trained using the Levenberg-Marquardt back pro- pagation algorithm. The inputs to the network consisted of 60,000 dataset of Reynolds number and relative roughness which were transformed to logarithmic scales. The performance evaluation of the model gives rise to a mean square error value of 2.456 × 10−15 and a relative error of not more than 0.004%. The error indices are less than those of previously developed neural network models and a vast majority of the non neural networks are based on explicit analytical approximations of the Colebrook equation.
Keywords:
Colebrook Equation, Explicit Models, Artificial Intelligence, Artificial Neural Network

1. Introduction
A fully developed fluid flow in a pipe of circular geometry is usually accompanied by a head or energy loss. This energy loss results from friction or shear resistance between the fluid layers and pipe walls. The Darcy-Weisbach [1] formula given by Equation (1) is commonly used to estimate the head loss based on the velocity of the fluid and the resistance due to friction.
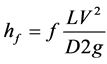 (1)
(1)
The evaluation of Equation (1) requires the friction factor to be known. In the laminar flow regime for both smooth and rough pipes, it is a function of the Reynolds number (Re) only. For turbulent flow in smooth pipes, f is a function of Reynolds only and is evaluated using the Prandtl-Von Karman [1] relation expressed in Equation (2)
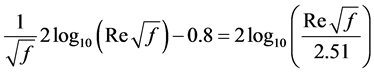 (2)
(2)
while for turbulent flow in rough pipes, Von-Karman relation [1] given in Equation (3) holds
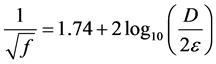 (3)
(3)
Colebrook [2] combined the above equations to arrive at his famous equation given in Equation (4). What he did was reported by Brkić [3] to be in violation of the mathematical laws of logarithm. However, the Colebrook equation has been a reference standard for friction factor prediction.
Friction factor, f, has to be known and can be determined from the Colebrook equation. This equation is, how- ever, implicit in relation to the friction factor. Therefore, its resolution requires an iterative solution.
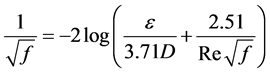 (4)
(4)
For calculations involving small data-sets, the iteratively solved Colebrook equation will generally suffice [4] . In industrial and engineering applications, large flow networks are essential to achieve continuous transport of material from different processing units. For the simulation of long pipes and networks of pipes, the Colebrook equation must be solved a huge number of times [5] . Therefore, an iterative solution to the implicit Colebrook equation is time consuming. The resolution of the implicit Colebrook equation has been of interest to researchers over the past seven decades. The numerous explicit approximations which abound in the literature attest to this fact. These approximations were developed using various conventional analytical approaches. They, however, vary in their accuracy and complexity, with the more complex ones having the capability to predict more accurately [6] . The performances of these approximations in relation to the Colebrook equation are well discussed in the literature [3] [6] - [9] .
Besides the conventional analytical approach to solving engineering problems, artificial intelligence techniques can be applied as they have in recent time matured to a point of offering practical benefits in many of their applications. Artificial intelligence refers to the ability to mimic/replicate the human behavior/reasoning into machines and software using cutting edge techniques. One of such techniques is the artificial neural network (ANN), an intelligent data-driven modeling tool which is able to capture and represent complex and non-linear input/output relationships from a set of examples [10] . Nowadays, artificial neural networks are being applied to a lot of real world problems, such as functional prediction/approximation, system modeling (where physical processes are not well understood or are largely complex), pattern recognition, etc., with the ability to generalize while making decisions about imprecise input data [11] .
The applications of artificial neural network to fluid flow for friction factor prediction have been reported [10] [12] [13] . The performance of the models developed is, however, low when compared with their non ANN based explicit counterparts. Previous studies have used datasets up to a maximum of 3000 for developing these models. This factor may have contributed to the low performances reported for these models. The Colebrook equation is non-linear and has a wide range of application i.e. 4000 ≤ Re ≤ 108, thus a small dataset will be insufficient to learn the input-output relationship across such range and produce a network which is able to predict friction factor with high accuracy. Brkić and Cojbasić [14] have developed an ANN model for predicting friction factor, a total of 90,000 dataset were used for a 2-50-1 network topology, and this gave rise to accuracy of 0.07% which was in close agreement with those of more accurate non ANN-based explicit friction factor models. As relationships between inputs and outputs are enriched, approximation capacity improves [11] .
This paper is aimed at developing an artificial neural network model for predicting friction factor using a multi layer perceptron network. The remaining sections of this paper are organized as follows: Section 2 provides an overview of artificial neural network. In section 3, the development of the proposed model is presented and the performance of the proposed model in comparison with those of the selected ANNs and non ANN-based explicit models is evaluated. In the final section, relevant conclusions are drawn based on the results obtained in this study.
2. Artificial Neural Network: Overview
Artificial neural network is the generalization model of biological nervous system [15] . It is in essence an attempt to simulate the human brain. Thus, it is a modeling tool which is able to learn complex and non-linear input-output relationships and reproduce same from a given set of examples by the use of neurons. It requires no prior knowledge of the mechanism/principles or background underlying the process to be modelled.
Ideally, a neural network consists of three distinct layers: input, hidden and output layers. The ability of an ANN to learn and approximate relationships between input and output is largely dependent on the size and complexity of the problem. The multi layer perceptron (MLP) is the most common amongst the types of ANN in which the data processing extends over more than one hidden layer. The hidden layer in MLP consists of layers of neurons.
The ability of an ANN to learn input-output relationship depends largely on the number of datasets used in training the network. A sufficiently large amount of datasets will enable the network learn accurately the input-output relationship of any given process [9] . The results obtained from the work of Shaya and Sablani [12] , Yazdi and Bardi [13] , Fadare and Ofidhe [10] and Brkić and Cojbasić [14] lend credence to this.
Prior to training of the network, the dataset are brought to the same order of magnitude (pre-processed). There are several normalization techniques but the most common are min-max, z-score and scaling. Min-max and its variant forms have been applied [10] [13] . The friction factor f, in the Colebrook equation has a logarithmic relationship with the Re and (ε/D), thus the adopted practice of taking the logarithmic transforms of the input parameters [12] [14] .
When training neural networks, calculus based search techniques such as back propagation are often used. Such search techniques are possible because the search space have been transformed (normalized) so that it is smooth [16] . When the search has succeeded, the neural network is said to have been trained, i.e. a suitable combination of connecting weights has been found. Details concerning the working of ANN abound in the literature.
3. ANN Model Development
3.1. Generation of Input-Output Dataset
The dataset used for developing the ANN model were obtained from the iterative solution of the implicit Colebrook equation using Microsoft Excel software. The dataset consisted of 60,000 values each of Reynolds number (4000 ≤ Re ≤ 108), relative roughness (10−6 ≤ (ε/D) ≤ 0.05) and friction factor, f. Reynolds number (Re) and ε/D are inputs to the network and f is as the target (the output variable) to be predicted by the network. These sufficiently large amounts of data set were used because the network may not be able to correctly learn the input-output relationship from a few dataset [14] . Although the training time maybe very long for a large data sets but will not affect the speed with which the network will predict.
3.2. Data Pre-Processing
Normalization helps to bring the data sets (input parameter) within the same order of magnitude. Several methods of normalization techniques exist, the z-score, min-max and the scaling. However, the min-max and its variant forms have been applied references [10] and [13] . The normalization approach used in this study is the same as used in [14] . In this approach, the input datasets were brought to a logarithmic scale by taking the logarithm to base 10 of Re, log10 (Re) and negative logarithm to base 10 of (ε/D), −log10 (ε/D), thus bringing the datasets to a range of 1.3 - 8. The friction factor term in the Colebrook equation shows that the Reynolds number and the relative roughness have logarithmic relationships; hence, most researchers have adopted the logarithmic forms of the Reynolds number and relative roughness.
3.3. The Proposed ANN Model
This work used the feed-forward (FF), multi layer perceptron network (MLP). Given the non-linearity in the Colebrook equation, the MLP network with non-linear transform functions could minimize the mean square error as performance determination [13] . The hidden layer consists of 2 layers with a predefined amount of neurons. A typical neural network structure with two hidden layers is as shown in Figure 1. The Re and ε/D are the inputs to the network while f is the output parameter. The “tansig” function was used as a non-linear transfer function in the hidden layers while the “purelin” function was used for the output layer.
3.4. Training the Network
The network was trained using the Levenberg-Marquardt back propagation algorithm. Besides, back propagation algorithms are also suitable for normalized data set because it is smooth and make the training easier [11] . By default, the MATLAB software partitions the data set in to 3 sets: the training data set (75%), test data set (15%) and validation data set (15%). The training dataset was used to do the training. The stopping criteria are usually determined by the preset error indices (such as mean square error, MSE) or when the number of epochs reaches 1000 (default setting). Several network topologies with two hidden layers were trained. However for this study, the number of epochs was set at 3000. The training process was truncated at only 51 epochs for a 2-30-30-1 network topology, having reached an MSE value of 2.456 ×10−15.
3.5. Performance Evaluation of the Model
The default performance index used by MATLAB for training the ANN model is mean square error (MSE).
 (5)
(5)
This index distributes the total error over the data points considered. However, it does not give any information about the performance of each individual data point. Figure 2 shows the performance of the training, testing and validation datasets compared with the Colebrook equation. The curves for these datasets are well superimposed. This is an indication that the ANN model is able to generalize with high accuracy.
To ascertain the robustness of this model, the relative error given in Equation (6) was also determined.
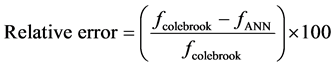 (6)
(6)
Table 1 gives a detailed error index of the ANN friction factor model for this study compared with the existing ANN friction models. The performance of the ANN model for this study based on relative error shows that it has error not exceeding 0.004%. This is a significantly high accuracy and compared with other ANN friction factor models, it ranks best. It can be seen from Table 1 that the models trained with a significantly large amount of dataset out performs those trained with a few datasets. In the study conducted by Brkić and Cojbasić [14] , a total of 90,000 datasets were used to develop a single layer ANN model with 50 neurons in the hidden layer. This resulted in an ANN model with relative error of not more than 0.07%. However, in this study, a total of 60,000 datasets with two hidden layers consisting of 30 neurons each were used. The accuracy of this model is 94% higher than the ANN model developed by Brkić and Cojbasić [14] which compensates for the additional neurons and hidden layers used in the model development for this study.
The performance of the ANN model proposed in this study was also compared with those of the extremely accurate non ANN-based explicit models, based on maximal relative and absolute errors criteria as shown in Table 2. The present ANN model ranks amongst the top four (4) most accurate friction factor models and can therefore conveniently be used in preference to other explicit approximations of the Colebrook equation.
Figure 1. A schematic of a typical ANN topology.
Figure 2. The performance of the training, test ad validation datasets after 56 epochs.
Table 1. Available ANN architectures for approximating the Colebrook equation.
Table 2. ANN Model for this study compared with the most accurate explicit friction factor models.
aEquation (2) in [17] . bEquation (3) in [17] . cEquation (2) in [18] . dEquation (6) in [18] . eEquation (2) in [19] . fEquation (4) in [19] .
4. Conclusion
A new ANN friction factor model is developed. The multi layer perceprton neural network with two hidden layers having 30 neurons each has relative error up to a maximum of 0.004% when compared with the Colebrook equation. When compared with the available non ANN-based explicit and existing ANN friction factor models, it out- performs the existing ANN models and compares well with the most accurate non ANN-based explicit models. Thus, the use of ANN for friction factor prediction has shown to be very successful based on the accuracy level obtained in this study. The accuracy of this model notwithstanding may not have been optimal. The performance of an ANN is sensitive to parameters such as the network topology, learning rate and the weight and bias. The optimal combination of these parameters can be found using evolutionary techniques such as genetic algorithm which have good global search ability. This will give the advantage of memory conservation and reduce the number of unnecessary parameters.
Cite this paper
Uchechukwu Herbert Offor,Sunday Boladale Alabi, (2016) Artificial Neural Network Model for Friction Factor Prediction. Journal of Materials Science and Chemical Engineering,04,77-83. doi: 10.4236/msce.2016.47011
References
- 1. Moody, L.F. (1944) Friction Factors for Pipe Flow. Transactions of the American Society of Mechanical Engineers, 66, 671-681.
- 2. Colebrook, C.F. (1939) Turbulent Flow in Pipes, with Particular Reference to the Transition Region between the Smooth and Rough Pipe Laws. Journal of the Institution of Civil Engineers, 11, 133-156.
http://dx.doi.org/10.1680/ijoti.1939.13150 - 3. Brkic, D. (2011) Review of Explicit Approximations to the Colebrook Relation for Flow Friction. Journal of Petroleum Science and Engineering, 77, 34-48.
http://dx.doi.org/10.1016/j.petrol.2011.02.006 - 4. Besarati, S.M., Myers, P.D., Covey, D.C. and Jamali, A. (2015) Modelling Friction Factor in Pipeline Flow Using a GMDH-Type Neural Network. Cogent Engineering, 2, Article ID: 1056929.
http://dx.doi.org/10.1080/23311916.2015.1056929 - 5. Clamond, D. (2009) Efficient Resolution of the Colebrook Equation. Industrial & Engineering Chemistry Research, 48, 3665-3671.
http://dx.doi.org/10.1021/ie801626g - 6. Asker, M., Turgut, O.E. and Coban, T.M. (2014) A Review of Non Iterative Friction Factor Correlations for the Calculation of Pressure Drops in Pipes. Bitlis Eren University Journal of Science and Technology, 4, 1-8.
- 7. Genic, S., et al. (2011) A Review of Explicit Approximations of Colebrook’s Equation. FME Transactions, 39, 67-71.
- 8. Winning, H.K. and Coole, T. (2013) Explicit Friction Factor Accuracy and Computational Efficiency for Turbulent Flows in Pipes. Flow, Turbulence and Combustion, 90, 1-27.
http://dx.doi.org/10.1007/s10494-012-9419-7 - 9. Yildirim, G. (2009) Computer-Based Analysis of Explicit Approximations to the Implicit Colebrook-White Equations in Turbulent Flow Friction Calculation. Advances in Engineering Software, 40, 1183-1190.
http://dx.doi.org/10.1016/j.advengsoft.2009.04.004 - 10. Fadare, D. and Ofidhe, U. (2009) Artificial Neural Network Model for Prediction of Friction Factor in Pipe Flow. Journal of Applied Science Research, 5, 662-670.
- 11. Magali, R.G., Meireles, P.E.M. and Marcelo, G.S. (2003) A Comprehensive Review for Industrial Applicability of Artificial Neural Networks. IEEE Transactions on Industrial Electronics, 50, 585-601.
http://dx.doi.org/10.1109/TIE.2003.812470 - 12. Shayya, W.H. and Sablani, S. (1998) An Artificial Neural Network for Non-Iterative Calculation of the Friction Factor in Pipeline Flow. Computer and Electronics in Agriculture, 21, 219-228.
http://dx.doi.org/10.1016/S0168-1699(98)00032-5 - 13. Yazdi, M. and Bardi, A. (2011) Estimation of Friction Factor in Pipe Flow Using Artificial Neural Network. Canadian Journal on Automation, Control and Intelligent Systems, 2, 52-56.
- 14. Brkic, D. and Cojbasic, Z. (2016) Intelligent Flow Friction Estimation. Computer Intelligence and Neuroscience, 2016, Article ID: 5242596.
http://dx.doi.org/10.1155/2016/5242596 - 15. Alabi, S.B. and Williamson, C.J. (2015) Neural Network-Based Model for Joint Prediction of the Newtonian and Non-Newtonian Viscosities of Black Liquor. International Journal of Chemical Engineering and Applications, 6, 195-200.
http://dx.doi.org/10.7763/IJCEA.2015.V6.480 - 16. Langdon, W.B. (1998) Genetic Programming and Data Structures. Volume 1, Springer Publishing, New York.
http://dx.doi.org/10.1007/978-1-4615-5731-9 - 17. Goudar, C.T. and Sonnad, J.R. (2008) Comparison of the Iterative Approximations of the Colebrook-White Equation. Hydrocarbon Processing: Fluid and Rotating Equipment, Special Report, 79-83.
- 18. Cojbasic, Z. and Brkic, D. (2013) Very Accurate Explicit Approximations for Calculation of the Colebrook Friction Factor. International Journal of Mechanical Sciences, 67, 10-13.
http://dx.doi.org/10.1016/j.ijmecsci.2012.11.017 - 19. Vantankhah, A.R. and Kouchakzadeh, S. (2008) Discussion of “Turbulent Flow Friction Factor Calculation Using a Mathematically Exact Alternative to Colebrook-White Equation” by Jagadeesh R. Sonnad and Chetan T. Goudar. Journal of Hydraulic Engineering, 134, 1187.
http://dx.doi.org/10.1061/(ASCE)0733-9429(2008)134:8(1187) - 20. Offor, U.H. and Alabi, S.B. (2016) An Accurate and Computationally Efficient Friction Factor Model. Advances in Chemical Engineering Science, 6, 237-245.
http://dx.doi.org/10.4236/aces.2016.63024
Nomenclature
f: Darcy friction factor [dimensionless].
D: Internal pipe diameter [m].
ε: Pipe absolute roughness [m].
ε/D: Relative roughness [dimensionless].
Re: Reynolds number [dimensionless].
L: Pipe length [m].
V: Flow velocity [m/s2].
g: Acceleration due to gravity.

Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/




