ABSTRACT

A large number of sparse signal reconstruction algorithms have been continuously proposed, but almost all greedy algorithms add a fixed number of indices to the support set in each iteration. Although the mechanism of selecting the fixed number of indexes improves the reconstruction efficiency, it also brings the problem of low index selection accuracy. Based on the full study of the theory of compressed sensing, we propose a dynamic indexes selection strategy based on residual update to improve the performance of the compressed sampling matching pursuit algorithm (CoSaMP). As an extension of CoSaMP algorithm, the proposed algorithm adopts a residual comparison strategy to improve the accuracy of backtracking selected indexes. This backtracking strategy can efficiently select backtracking indexes. And without increasing the computational complexity, the proposed improvement algorithm has a higher exact reconstruction rate and peak signal to noise ratio (PSNR). Simulation results demonstrate the proposed algorithm significantly outperforms the CoSaMP for image recovery and one-dimensional signal.

Keywords:

Compressed Sensing, Residual Descent, Reconstruction Algorithm, Backtracking

1. Introduction

Compressed Sensing (CS) is a new theory of signal processing, proposed by [1] [2] . If the sampled signal has sparsity or compressibility, the original signal can be recovered well by sampling only a small number of data points and selecting the reconstruction algorithm reasonably. There are a variety of sparse signals in nature, which brings broad prospects for the use of compressed sensing [3] [4] [5] . In order to efficiently reconstruct the original signal, a lot of algorithms have been proposed to solve this problem. They are mainly divided into three categories: greedy pursuit, convex optimization and combination algorithm. Greedy pursuit has been widely used owing to its low computing complexity and high reconstruction speed. Tropp and Gilbert propose Orthogonal Matching Pursuit (OMP) in 2006. Later, some modified algorithms are proposed, such as Stagewise Orthogonal Matching Pursuit (StOMP) [6] , Stagewise Weak Orthogonal Matching Pursuit (SWOMP) [7] ; these algorithms have low reconstruction complexity but require more measurements to perfect reconstruction. Subspace Pursuit (SP) [8] [9] [10] [11] introduced the idea of backtracking which can offer better reconstruction quality and low reconstruction complexity, but it needs the sparsity level K as a prior information. Bayesian Group Matching Pursuit (GMP) [12] [13] , whose group coefficients are modeled by a multivariate Gaussian distribution, and solved by a maximum a posteriori probability estimate, has a better reconstruction in solving the reconstruction problem.

The reconstruction algorithm is the core of CS theory. How to efficiently recover low-dimensional signals to high-dimensional signals is the goal pursued by many researchers. The difficulty with this problem is that reconstruction of high-dimensional signals requires solving an underdetermined equation. So the problem can be solved by the l₀ norm minimization, which is an NP-hard problem [14] that requires exhaustively listing all possibilities of the original signal and is difficult to achieve by the traditional algorithm.

In this paper, the improved CoSaMP reconstruction algorithm based on residual update was proposed, which is an improved algorithm in view of the CoSaMP. We propose a dynamic indexes selection strategy based on residual update to improve the performance of the compressed sampling matching pursuit algorithm (CoSaMP). This backtracking strategy which is based on this residual descent can flexibly select backtracking indexes. And this improvement can improve the reconstruction performance. Different simulation results show that the improved algorithm has better reconstruction performance for both one-dimensional signals and two-dimensional signals compared with other classical algorithms.

The rest of this paper is organized as follows. Section 2 introduces the background and the improved algorithm. We discuss the performance of proposed algorithm in Section 3 and conclude the paper in Section 4.

2. Compressive Sensing Model and Greedy Algorithm

2.1. Compressive Sensing Model

We suppose that x is an $N\times 1$ sparse signal. CS suggests that one can recover certain signal from far fewer samplings or measurements than traditional methods via the following optimization problem:

$\underset{x}{\min }{\Vert x\Vert }_0\text{s}\text{.t}\text{.}y=\Phi x.$ (1)

where ${\Vert x\Vert }_0$ indicates the number of nonzero elements in x. The $\Phi$ denotes the random measurement matrix $\left(\Phi \in R^{M\times N},M\ll N\right)$ . But, zero-norm minimization problem is NP-hard. The solution to the one-norm problem is convex relaxation of zero-norm. As the computational intractability, this problem could be replaced by one-norm optimization problem:

$\underset{x}{\min }{\Vert x\Vert }_1\text{s}\text{.t}\text{.}y=\Phi x.$ (2)

where ${\Vert x\Vert }_1$ represents the sum of absolute value of non-zeros components of x. And linear programming methods have shown to be effective in solving such problems (2) with high accuracy. Such as BP. Theoretically, Candes also proved that when the random measurement matrix satisfies the restricted isometry property (RIP) [15] [16] , Equation (2) is equivalent to Equation (1). The following definition of restricted isometry property (RIP) of sensing matrix $\Phi$ plays an important role on the analysis of recovery algorithm in CS.

Definition 1. For the sensing matrix $\Phi$ , each integer $s=1,2,\cdots$ , the $\Phi$ satisfies the restricted isometry property of order s if

$\left(1-{\delta }_s\right){\Vert x\Vert }_2^2\le {\Vert \Phi x\Vert }_2^2\le \left(1+{\delta }_s\right){\Vert x\Vert }_2^2$ (3)

holds for all s-sparse vectors $x\in R^N$ and some $0\le {\delta }_s<1$ . The restricted isometry constant (RIC) ${\delta }_s$ is the smallest value.

But minimizing the l₁ norm is very complicated and requires a lot of calculations. However, the greedy reconstruction algorithm has a simple geometry and a very low computational complexity. So, greedy algorithm is widely used for sparse reconstruction.

2.2. Compressed Sampling Matching Pursuit Algorithm

As we all know, the OMP algorithm first proposed the idea of orthogonality. Many subsequent algorithms follow this idea. OMP algorithm selects only one index which is corresponding to the largest magnitude. Through this method, index selection is inefficient. And OMP does not adopt backtracking mechanism. Once an error occurs in the support set selection process, it will result in poor reconstruction. For CoSaMP algorithm, it selects multi-indexes in each iteration, which can promote the reconstruction speed. However, if the selected indexes is not appropriate for signal reconstruction, it would remove fixed indexes from temporary support sets to get high reconstruction quality and accuracy. The CoSaMP algorithm is summarized in Table 1.

2.3. The Proposed Algorithm

Since the CoSaMP algorithm returns a fixed number of indexes in the backtracking phase, it is added to the support set. These indexes may be errors with a high probability. Once a high probability error occurs, it will have a great impact on the reconstruction results. We propose a backtracking index dynamic selection strategy based on residual descent. We can dynamically adjust the number of backtracking indexes based on changes in the residuals. The proposed algorithm is summarized in Table 2.

3. Simulations and Analysis

In this part, we verify the performance of the proposed sparse signal reconstruction algorithm based on residual update and compare it with several most advanced reconstruction algorithms. We comprehensively verify and contrast the proposed algorithm from one-dimensional random sparse signals and two-dimensional image signals. And we have detailed each experiment.

3.1. One-Dimensional Signal

In this section, in order to demonstrate the superiority of the proposed algorithm, we compare the proposed algorithm with other similar classical algorithms for signals with nonzero elements drawn from the Gaussian and uniform distributions. Gaussian sparse signals are used with length N = 256 and sparsity level K = (5, 20). The sensing matrix $\Phi$ , which is different for each test signal, is drawn from the Gaussian distribution with mean 0 and standard deviation 1/N. Then, we normalize each column norm to unity. Experimental platform was MATLAB R2013b.

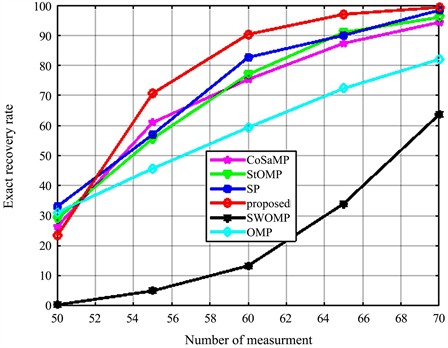
As shown in Figure 1, we provide the rate of exact reconstruction performance as a function of the measurement number M. Figure 1 shows the curves of the probability of exact recovery signal with the proposed algorithm. 500s simulations were conducted for the different number of measurements M. The exact recovery rate of the proposed algorithm at M = 60 increases by 90%. And overall, the algorithm proposed in this paper is also superior to other classical algorithms in Figure 1.

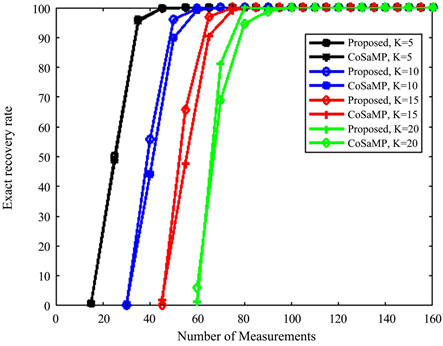
Figure 2 shows the curves of the probability of exact recovery signal with the proposed algorithm. It shows the comparison of the exact reconstruction rate of the proposed algorithm and CoSaMP algorithm under different sparsity level (i.e., 5, 10, 15, 20 non-zero entries). 500 simulations were conducted for each pair of sparsity k and the number of measurements M. Figure 2 also shows the proposed algorithm has higher probability of exact recovery signal.

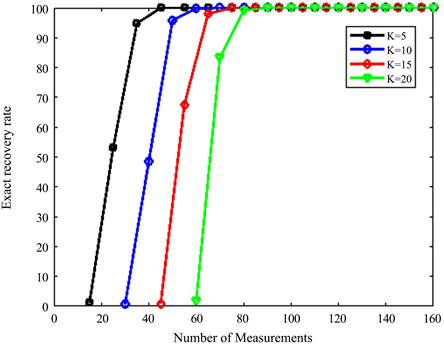
Figure 3 shows the curves of the probability of exact recovery signal with proposed algorithm. The number of measurements (M), given a fixed signal sparsity K. 500 simulations were conducted for each pair of sparsity K and the number of measurements M. Figure 3 shows that the proposed algorithm has higher stability and reliability in terms of exact recovery of the signal.

3.2. Two-Dimensional Signal

In the two-dimensional image experiment, the wavelet base is used as the sparse basis and the random Gauss matrix is used as the measurement matrix $\Phi$ . We use three international standard, i.e. Lena image, Camera image and Barche image, as the input to conduct the comparison analysis of different algorithms. And the peak signal-to-noise ratio (PSNR) is used to evaluate the performance of the improved algorithm and the original algorithm, which is defined as follows

$\text{PSNR}=10{\log }_{10}\left(\frac{M\times N\times {255}^2}{{\Vert x-\tilde{x}\Vert }_2}\right)$ (4)

where x is the original image, $\tilde{x}$ is the reconstruction image. Sampling ratio is M/N. The size of each image is 256 × 256.

From Figure 4, we can know that the proposed algorithm is superior to the original algorithms CoSaMP. And we can see that the proposed algorithm has a better visual effect for different types of images. The improved algorithm can accurately recover the original signal.

4. Conclusion

Based on a comprehensive study of the sparse signal reconstruction algorithm, we find that CoSaMP cannot dynamically select the support set to efficiently reconstruct the original signal. To solve this problem, we use the residual update strategy to improve the backtracking index selection. Thereby the number of backtracking indexes is adjusted according to the direction in which the residual is decreasing. The proposed algorithm can significantly improve the performance of CoSaMP by adjusting dynamically the number of indexes which are added to the support set in each iteration. Different simulation results show that the improved algorithm has better reconstruction performance for both one-dimensional signals and two-dimensional signals compared with other classical algorithms.

Acknowledgements

This research has been supported by National Natural Science Foundation of China under Grant No. 61771262, and Science and Technology Major Project and Engineering of Tianjin China under Grant No. 2017ZXHLNC00100.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

Cite this paper

Lu, D.X., Sun, G.L., Li, Z.Z. and Wang, S.J. (2019) Improved CoSaMP Reconstruction Algorithm Based on Residual Update. Journal of Computer and Communications, 7, 6-14. https://doi.org/10.4236/jcc.2019.76002

References