Received 19 June 2016; accepted 18 July 2016; published 21 July 2016

ABSTRACT

Soft computing is a combination of methods that complement each other when dealing with ambiguous real life decision systems. Rough Set Theory (RST) is a technique used in soft computing that enhances the idea of classical sets to deal with incomplete knowledge and provides a mechanism for concept approximation. It uses reducts to isolate key attributes affecting outcomes in decision systems. The paper summarizes two algorithms for reduct calculation. Moreover, to automate the application of RST, different software packages are available. The paper provides a survey of packages that are most frequently used to perform data analysis based on Rough Sets. For benefit of researchers, a comparison of based on functionalities of those software is also provided.

Keywords:

Rough Set Theory, Soft Computing, Reducts, Rosetta, Rough Sets, Decision Table, RSES, Rose2, WEKA

1. Introduction

One common aspect among the fields of machine learning, decision analysis, data mining and pattern recognition is that all of them deal with imprecise or incomplete knowledge. As a result, it is imperative that appropriate data processing tools must be employed when researching computational intelligence and reasoning systems [1] . Soft computing provides a blend of such data processing mechanism that masters the art of processing vague or imprecise knowledge encountered in real life problems [2] [3] . Fuzzy logic by Zadeh [4] is the technique at the forefront of soft computing. It adds the idea of degree association (membership functions) to the classical set theory. Rough Set Theory (RST), put forth by Pawlak [5] offers another approach of dealing with imprecise knowledge that is quite different from fuzzy logic.

Since its development Rough Set Theory has been able to devise computationally efficient and mathematically sound techniques for addressing the issues of pattern discovery from databases, formulation of decision rules, reduction of data, principal component analysis, and inference interpretation based on available data [6] [7] . The paper explores different algorithms of calculating key attributes in a decision system and reviews the most common software packages used to automate the application of analysis based on RST.

The rest of the paper is organized as follows: Section 2 presents a brief review of rough sets, reducts and several algorithms used to compute reducts. Section 3 presents survey of a number of software packages used to automate application of RST. These include Rosetta, RSES, Rose2, Rough Sets, and WEKA. Section 4 shows a comparison of the different components of the packages surveyed in section 3. Conclusion, future work and references are presented at the end.

2. Rough Sets

The Rough Set Theory has had a significant impact in the field of data analysis and as a result has attracted the attention of researchers worldwide. Owing to this research, various extensions to the original theory have been proposed and areas of application continue to widen [8] . As Jensen [1] observes, many rough set based clinical decision models are available to assist physicians, in particular the inexperienced ones, to recognize patterns in symptoms and allow for quick and efficient diagnosis. Results available support the premise that systems based on RST give accuracy and reliability that is comparable to Physicians though accurate input data is required. Such systems, in conjunction with other ICT facilities, can be particularly helpful in remote areas of developing countries where healthcare infrastructure is patchy [9] . Detailed discussion on Rough Sets has been presented by the authors in [10] .

2.1. Reduction of Attributes (Reducts)

While studying decision systems, all researches confront the question of dropping some (superfluous) condition attributes without altering the basic properties of the system [7] . Rough Set Theory provides a sound mechanism of carrying out this task. The process is referred as attribute reduction or feature selection [1] [11] . The reduct thus obtained retains the minimal set of attributes that preserves the information of interest. Decision rules are then deduced based on these reducts [12] . The procedure adopted may be represented as shown in Figure 1.

The idea can be more precisely stated as: Let C, 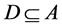be subsets of condition and decision attributes. We can say that 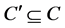is a D-reduct (reduct with respect to D) of C, if 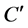is a minimal subset of C such that

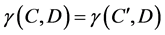(1)

where 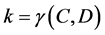is the Consistency Factor. If k = 1 we say that decision D depends totally on C, and if k < 1, we say that D is partially dependent on C. Therefore, removing the condition attribute doesn’t alter the consistency factor.

Any given information system may have a number of reduct sets. The collection of all reducts is denoted as

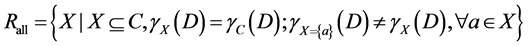(2)

For many tasks, such as feature selection, it is necessary to search for the reduct that has the minimum cardinality () i.e.. 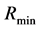can be represented as

(3)

2.2. Calculation of Reducts

As Komorowski [13] has stated, it can be shown that the number of reducts of an information system with m

attributes may be equal to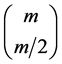. This means that calculation of reducts can a tedious task and is, in fact, one

of the bottleneck of the rough set methodology. For tunately, several algorithms have been developed to calculate reducts particularly in cases when the information system is large and involves a number of attributes [11] [13] [14] . An algorithm referred as Quick Reduct Algorithm adapted from [15] has been shown in Figure 2. The algorithm attempts to calculate reducts by starting with an empty set and continue to add attributes with greatest increase in rough dependency metric, one by one, until the maximum possible value for the set is reached.

2.3. Johnson Algorithm for Reducts

Johnson Algorithm is a famous approach to calculate reducts and extract decision rules from a decision system [16] . It is a heuristic algorithm that uses a greedy approach for calculation of reducts. It always selects the most frequent attribute in decision function or a row of decision matrix and continues till the reducts are obtained. The algorithm is represented in Figure 3.

This algorithm considers attribute occurring most frequently as most significant. Although, this is not true in all cases, but it generally finds out an optimal solution. Application of both the algorithms presented here onto the decision systems can be automated. The software used for the said purpose are stated consequently.

3. Software Packages for Rough Sets

To apply RST on datasets, a number of software systems have been developed by computer scientists across the globe. This development can be attributed to the successful application of rough sets to data mining and knowledge discovery. A brief review of most commonly used software is presented. Details of the software can be obtained by referring existing literature or contacting respective authors [17] - [19] .

3.1. Rough Sets [20]

It is a free package for R language that facilitates data analysis using techniques put forth by Rough Set and Fuzzy Rough Set Theories. It does not only provide implementations for basic concepts of RST and FRST but also popular algorithms that derive from those theories.

The development of the package involved Lala Septem Riza and Andrzej Janusz as Authors; Dominik Ślęzak, Chris Cornelis, Francisco Herrera, Jose Manuel Benitez and Sebastian Stawicki as Contributors; and Christoph Bergmeir as Maintainer. The functionalities provided by the package include Discretization, Feature selection, Instance selection, Rule induction, and Classification based on nearest neighbors. The main functionalities are summarized in Figure 4.

3.2. Rough Set Exploration System (RSES)

RSES is a toolset used for analysis of data using concept of the Rough Set Theory. It has a user friendly Graphical User Interface (GUI) that run under MS Windows^® environment. The interface provides access to the methods that have been provided by RSES lib library, the core computational kernel of RSES [21] . The library as well as the GUI has been designed and implemented by the Group of Logic at Institute of Mathematics, Warsaw University and Group of Computer Science at Institute of Mathematics, University of Rzeszów, Poland [22] . The sequence of steps followed by RSES to perform analysis based on RST is shown in Figure 5.

As stated on their website, the system was designed and implemented as a result of research on Rough Set led by Andrzej Skowron (Project Supervisor) and team involving Jan Bazan, Nguyen Hung Son, Marcin zczuka, Rafał Latkowski, Nguyen SinhHoa, Piotr Synak, Arkadiusz Wojna, Marcin Wojnarski and Jakub Wróblewski. RSESlib is a library that provides functionalities for performing a number of data exploration tasks including:

Ÿ Decomposition of large data sets into fragments that have the same properties.

Ÿ Manipulation of data.

Ÿ Discretization of numerical attributes.

Ÿ Calculation of reducts.

Ÿ Generation of decision rules.

Ÿ Search for hidden patterns in data.

The library has been implemented in C++ and Java. The development took place between 1994 and 2005. First version of library, after several extensions was included in the computational kernel of the Rosetta system.

3.3. Rosetta

The Rosetta system (Rough Set Toolkit for Analysis of Data) is a toolkit for analyzing datasets in tabular form using Rough Set Theory [17] [21] . It implements rough-set based rule induction as well as a number of additional features such as discretization algorithms, clustering techniques, reduct computation, classifiers, rule pruning and classifier evaluation [23] . It has been designed to support the overall procedure of data mining and knowledge discovery i.e. from initial pre-processing of data to finding the minimal set of attributes (reducts), generation of IF-THEN rules, partition of data for training and testing purpose, and validation as well as analysis of induced rules and patterns. If also provides facility to generate tables, graphs and comparison matrices [24] .

Rosetta has been developed as a general purpose tool for modelling based on discernibility and not geared towards any particular application domain. This is the reason why it has been used by a large community of scientists [23] working in different areas of application. It offers a highly user friendly GUI environment that offers data navigation. All the objects that can be manipulated are shown as individual GUI items with dedicated context menus to further resolve the task further. Moreover, the computational kernel is available as a command line program invokable from common scripting languages such as Perl or Python.

Rosetta has been developed by two groups: Knowledge Systems Group Norwegian University of Science and Technology, Trondheim, Norway and the Group of Logic, Inst. of Mathematics, University of Warsaw, Poland under the guidance of Jan Komorowski and Andrzej Skowron [25] . Main design and programming of GUI was accomplished by the group in Norway under Aleksander Øhrn while library of rough set algorithms (RSES) was developed in Poland. The notable features of the kernel are shown in Figure 6. A brief description of functionalities follows:

1) Data import/export.

a) Ability to integrate with other DBMS using ODBC.

b) To export tables, graphs, induced rules, and reducts etc. to a variety of formats, including plain text, XML,

Matlab and Prolog.

2) Pre-processing.

a) Discretization of numerical attributes.

b) Completion of missing values in decision tables using different algorithms.

c) Partition of data into training and testing groups using random number generators.

3) Computation.

a) Efficient computation of reducts.

b) Provides support for supervised and unsupervised learning.

c) Generation of IF-THEN rules using reducts.

d) Execution of script files.

e) Support for cross validation.

4) Post processing.

a) Advanced filtering of sets of reducts and rules.

5) Validation and analysis.

a) Application of induced rules on testing data.

b) Generation of confusion matrices and ROC curves.

c) Supports statistical hypothesis testing.

6) Miscellaneous.

a) Performs clustering using tolerance relations.

b) Computes variable precision rough set approximations.

c) Support for random sampling of observations.

3.4. Rose2

ROSE (Rough Sets Data Explorer) is another software that implements Rough Set Theory and other techniques for rule discovery [26] . The Rose2 system is a successor of Rough DAS and Rough Class systems which is regarded as one of the first successful implementation of the Rough Set Theory. It has also been used in many real life applications [18] . It has been developed at Laboratory of Intelligent Decision Support Systems of the Institute of Computing Science in Poznan, Poland after years of research on rough set based knowledge discovery and decision support [27] .

Rose2 provides number of tools for knowledge discovery based on rough set (shown in Figure 7). These include processing of data, discretization of numerical attributes, carrying out data reduction by searching core and

reducts of attributes, inducing sets of decision rules from rough approximations of decision classes and using them as classifiers, and evaluating sets of rules on testing data in classification experiments.

3.5. Waikato Environment for Knowledge Analysis (WEKA) [28]

The project WEKA, Waikato Environment for Knowledge Analysis [28] , is a machine learning software suite developed at the University of Waikato, New Zealand. It provides tasks such as data processing, classification, clustering, association, regression and visualization (shown in Figure 8). It is also suited for making new schemes in machine learning. It is a GUI based software that provides menus to carry out the functions stated above. The analysis can be applied to dataset as well integrated with JAVA code.

4. Comparison of Software

A comparison of different components offered by the Rough Sets, Rose2, Rosetta, RSES, and WEKA is provided in Table 1. A more detailed comparison can be referred in [20] .

The components listed include:

Ÿ Technique used in the package.

Ÿ Programming language used to develop the package.

Ÿ The Operating System that the package supports.

Ÿ The type of user interface provided.

Ÿ Whether or not package provides calculation of basic concepts of rough sets such lower, upper approximation, boundary sets etc.

Ÿ Whether the package provide the facility of feature/instance selection.

Ÿ Can the package divide the data into training and test sets as per requirement of the user?

Ÿ Can the package induce decision rules based on reducts?

Ÿ Can data be classified on the basis of nearest neighbor based algorithms?

Ÿ Does package provide the facility of cross validation to determine the accuracy and reliability of classification?

5. Conclusions and Future Work

Soft Computing lies at the foundation of computational and conceptual intelligence. It exploits the tolerance of imprecision, uncertainty and partial information to mimic human mind like thinking ability and calculating decisions. Rough Set Theory is an adaptable technique that uses approximation sets to represent a vague concept. The calculations of RST can be cumbersome for large datasets but many existing software can be effectively used to automate them. A number of software has been briefly presented together with the main functionalities provided.

Our future work will explore application of RST on real datasets using some of the software presented and formulation of a step-by-step guide for other researchers to explore and adapt.

Cite this paper

Zain Abbas,Aqil Burney, (2016) A Survey of Software Packages Used for Rough Set Analysis. Journal of Computer and Communications,04,10-18. doi: 10.4236/jcc.2016.49002

References

NOTES

^*Corresponding author.