Journal of Computer and Communications
Vol.03 No.10(2015), Article ID:60533,8 pages
10.4236/jcc.2015.310002
Apply AHP for Resource Allocation Problem in Cloud
Avtar Singh, Kamlesh Dutta
Department Computer Science Engineering, National Institute of Technology, Hamirpur, India
Email: avtarz@gmail.com, Kd@nith.ac.in
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 31 August 2015; accepted 20 October 2015; published 23 October 2015
ABSTRACT
Cloud computing is an emerging paradigm with many applications that are integrated with IT organization having the freedom to migrate services between different physical servers. Analytic Hierarchy Process (AHP) with a pairwise comparison matrix technique for applications has been used for serving resources. AHP is a mathematical technique for multi-criteria decision-making used in cloud computing. The growth in cloud computing for resource allocation is sudden and raises complex issues with quality of services for selecting applications. Finally, based on the selected criteria, applications are ranked using the pairwise comparison matrix of AHP to determine the most effective scheme. The presented AHP technique represents a well-balanced multi criteria priorities synthesis of various applications effect factors that must be taken into consideration when making complex decisions of this nature. Keeping in view wide range of applications of cloud computing an attempt has been made to develop multiple criteria decision making model.
Keywords:
Cloud Computing, Analytic Hierarchy Process, Consistency Ratio (CR), Consistency Index (CI)

1. Introduction
Cloud computing is becoming an increasingly popular computing model in which computing resources are made available on-demand to the user as needed [1] -[4] . Cloud computing provides many opportunities for enterprises by offering a range of computing services [5] [6] . The benefits of cloud computing include services on low costs and capital expenditures, increased operational efficiencies, scalability, flexibility and so on. Cloud computing provides different types of services, which are categories in three main layers such as I) SaaS (Software as a Service); II) PaaS (Platform as a Service); III) IaaS (Infrastructure as a Service) and provides many chances for enterprises by offering a range of computing services. These chances, still, don’t come without challenges. Dynamic resource allocation is also a challenge in cloud computing. A complex mathematical decision model associated with the selection of cloud computing services in a multi-source scenario is presented [7] . PaaS by evaluating ranking framework solutions according to the needs is required and also proposed a set of benchmarking algorithms that can help determine the suitable PaaS provider based on different resources and applications requirement [8] . When many users make requests for cloud resources at the same time, then how these requested and other resources will be allocated to users to get resources. This is a challenging task in cloud computing. Consider the following (hypothetical) example: an application that needs to define technical specifications for its cloud applications with various criteria that are important to them. When several applications are offered by different vendors, the selection of particular application becomes a key issue [9] . It involves analysis of selection parameters and attributes of applications. As multiple criteria are involved in decision making, it is a multi- criteria decision-making (MCDM) problem. Being a problem involving multi-criteria and different application, it can’t be solved with mere assessment. The assessment may work fine, only when the selected parameters and attributes of applications are few. During the selection process, generally the characteristics are ranked or prioritized. The prioritization includes deciding the weights of parameters. While considering the weights of parameters, it is quite likely that the user’s assessment may be based towards the key factors only. This may lead to improper priority and incorrect weights being assigned to the parameters. To make an appropriate decision, it is necessary to have a quantifiable value rather than subjective opinions. To deal with this problem we have proposed analytical hierarchy process which is widely accepted by the experts. AHP brings an ability to judge the consistency in the analysis process and helps to reduce deviations. Continuation of this paper includes AHP selection parameters based on literature study, methodology adopted and application of AHP to the problem followed by a conclusion.
2. AHP Methodology
AHP is a mathematical technique used for multi-criteria decision-making. This is better than other multi-criteria techniques. It's designed to incorporate tangible as well as non-tangible factors, especially where the subjective judgments of different individuals constitute an important part of decision making [10] [11] . The pros of AHP over other multi criteria, methods are its flexibility, intuitive call to the decision makers and its ability to check inconsistencies. Normally, users find the pairwise comparison form of data input straightforward and convenient. The following (Table 1) shows the values and their description used for the comparison of relevant values of the elements of a typical AHP model.
This technique proposed on weight priorities and ranking mechanism of task based on correctness of consistency ratio is proved mathematically and multi criteria evaluation hierarchy [12] . A suggested framework for ranking of cloud computing services [13] . The drawbacks of AHP in its invariable weight system and improved ranking approach [14] . This scenario is proposed where you need to prioritize two requirements having different weight at different time and the limitations of AHP in a practical environment [15] . SaaS products are made
Table 1. Fundamental scales 1 to 9.
available in a cloud computing environment that uses AHP to prioritize product characteristic based on an expert scoring system [16] . The following method for calculating inconsistency [11] . The cons of the AHP technique are the limitation scale that uses 9-point. Sometimes, the decision maker might find difficult to differentiate among them and express for example, whether one alternative is 7 or 8 times more important than another. Given k tasks, e.g. attributes or alternatives, author supposed the decision makers are able to compare any two of them.
2.1. Consistency
Saaty TL has proposed a consistency index CI which is related to the Eigen value method.
 (1)
(1)
where n = dimension of the matrix, 𝜆max = maximum Eigen value.
The consistency ratio, the ratio of CI and RI, is given by:
CR = CI/RI (2)
where RI is the random index (the average CI of 500 randomly filled matrices).
If CR is less than 10%, then the matrix can be considered as having an acceptable consistency [10] [17] [18] calculated the random indices shown in (Table 2) which gives the average inconsistency. Mathematically, inconsistency is not, but a rescaling of the largest eigenvalue. Since 𝜆max ≥ n and CIn is always non-negative. The inconsistency index in its own has no meaning, unless we compare it with some benchmark to determine the magnitude of the deviation from consistency. However, the revision process stops at the requirement that consistency ratio CR ≤ 0.1, which may not obtain a superior CR. Decision theory helps the decision maker in selecting the best course of action from the available courses of action. The decision model is classified such that the type of information which is given about the state occurrence of the various state nature as well as depending upon the decision environment. There are four different states of decision environments: certainty, uncertainty, risk and conflict. AHP uses a five-step process to solve decision problems are as follows:
I. Create a decision hierarchy by breaking down the problem into a hierarchy of decision elements.
II. Collect input by a pairwise comparison of decision elements.
III. Determine whether the input data satisfies a consistency test. If it does not, go back to Step II and redo the pairwise comparisons.
IV. Calculate the relative weights of the decision elements.
V. Aggregate the relative weights to obtain scores and hence rankings for the decision alternatives.
The first two steps are related to the popularity of AHP, which are decision maker involved in the model that does not require advanced knowledge of either mathematics or decision analysis to perform [19] . The rest of the three steps are computed and can be performed manually or by using software. AHP has a reference architec- ture with self-contained tightly integrated design with reliable, flexible and automated. Cloud computing provides numerous types of users with different services. In the cloud computing, the following four parameters of QoS need to be considered as input for our case but not restricted to this because there are other parameters too [20] .
2.2. The Completion Time
The correctness of QoS comprises start time, the latest completion time, total completion time, finish time and so on. We select the total completion time (the time interval that a task is submitted to the completion) as the assessment index. TF represents the execution time of task Ti, it can be depicted as (3).
TF = Twait + Texec + Ttrans (3)
Table 2. Random indices (RI).
Twait represents the waiting times, Texec stands for the task execution time, Ttrans means the task transmission time. For customers of real time necessity, it expects the tasks should be completed in as little time as possible.
2.3. Bandwidth
Bandwidth needs for adjustment to the application of regular communication, which customers demand higher communication bandwidth. For multimedia traffic demand, it needs to study bandwidth first. Usually, bandwidth depends on the bandwidth value of ISP that provides cloud computing services. Simultaneously, it is related to the customer's local host configuration. Commonly, in the cloud computing services, bandwidth is a fixed quantitative value. It can be depicted as (4).
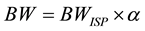 (4)
(4)
BW represents the actual bandwidth value, BWISP means the service bandwidth that ISP provided, α is the line factor that access to the services. For example, the same service provides customer’s bandwidth is not same for all the services such as LAN and ADSL, because the quality of the lines.
2.4. Reliability
Customers with lengthy tasks, cloud computing must deliver a stable and reliable performance, such as cloud storage service. Customers with lengthy tasks, may fail because resource lost its strength. Selecting high reliability of the resources in cloud computing can improve the quality of its services significantly. Generally, reliability of network can be measured by MTBF (Mean Time Between Failures) and MTTR (Mean Time To Repair). They can be depicted as (5) and (6).
MTBF = 1/λ (5)
𝜆 stands for the average fault cycle
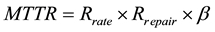 (6)
(6)
Rrate denotes the fault response speed, R repair means the fault repair speed, β is the failure treatment factor.
2.5. Cost
Cloud computing pays a fee as essential. The usage charges are an element that customers are concerned about. Customers who want the low cost service will set the cost as a measurable standard of the cloud computing. We can depict the costs of the virtual machines as (7):
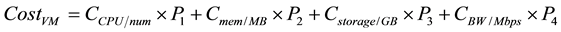 (7)
(7)
Pi represents the amount of resources, C is the resource costs of units.
2.6. Problem Modeling
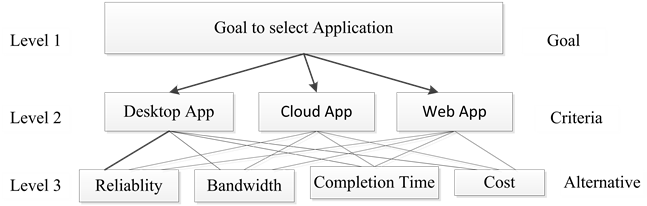
Unpredicted growth in cloud computing for resource allocation raises complex issues with quality of services for selecting applications to minimum cost, migration by balancing work where and when needed. Three criteria were considered while designing the components. They are Desktop app (DA), Cloud app (CA) and Web app (WA). CA is an application program that function in the cloud with some characteristics of pure web app. DA occupies totally on a single device at the user’s location. WA is stored totally on remote server and is delivered over the internet through browser interface. The structures of these components (reliability, bandwidth, cost, completion time etc) are given in the (Figure 1) AHP is selected as the method of decision process. The priorities will be derived from a sequence of size: pairwise comparisons involving all the components. The comparisons will start by comparing the alternatives with respect to their strengths to meet each of the criteria. The next step will be to compare the criteria with their importance to the goal. Since we have three alternatives and need to compare with each other, we will make three pairwise comparisons with respect to each criterion: DA vs.CA, CA vs. WA, and WA vs. DA.
To solve the hierarchy following steps are needed and discussed below.
Figure 1. Hierarchy of selection process.
2.7. Formation of Hierarchy
In the real world, decision-making problems are filled with uncertainty. The decision hierarchy formulated by breaking down the problem into a hierarchy of decision components. Systematic step to find the requirement for selective application. The application can be Desktop app (DA), cloud app (CA) and Web app (WA). In offline the desktop app and cloud app will respond faster. While in online cloud app and web app need not permanently engaged on the local device. Cloud app is user control of storage. The user has a reasonably fast Internet connection, a good code cloud app extends all the interactivity of a desktop app by with the portability of a Web app.
2.8. Collection of Inputs
AHP is used as a tool for systematically analysis the subjective judgments of several experts belonging to the various fields in this step. To avoid bias that can be presented on judgments are considered from single expert user needs more expert consulting. Hence, for selection three different states an expert for decision making. The nominal ratio scale of 1 to 9 is adopted for pairwise comparison [11] .
2.9. Consistency Tests
The results of pair wise comparisons are filled in positive reciprocal matrices to calculate the eigenvector and eigen value. The consistency of the judgments is determined by a measure called consistency ratio (CR). The consistency ratio is obtained to filter out the inconsistent judgments, when the value of the consistency index (CI) < 0.1. All the judgments are found to be consistent and accepted for analysis.
2.10. Calculation of Relative Weights & Ranking of Alternatives
The geometric mean method has been the most widely applied methods in AHP for aggregation of individual preferences when more than one expert is involved in the decision-making. All the expert opinions are consistent, but entirely different from other. Geometric mean of individual opinions is calculated and entered in the final judgmental matrix for finding out the ranks of the alternatives.
3. Result and Analysis
The framework uses an AHP technique for prioritization
For using AHP
{
Create total of all attribute such as reliability, bandwidth, completion time and cost with consistency
}
Calculate the weight by GM
Find the weight associated with each application. The propose framework will select an application by the relative weight level value associated with each application. For the sake of better understanding of the benefit of proposed scheme, we have investigated the priority vectors (PV) that are acceptable to a different user for data collection. The next level 2 will be to compare pairs of alternatives with respect to Reliability. The decision taken will decide for each comparison which alternative is the lower with respect to Reliability, giving its reliability a weight of 1. Using the AHP Fundamental Scale (Table 1). the Decision Makers will assign a weight to the reliability of the other alternative. The comparisons are summarized below in (Table 3).
The next level is to weight matrix, by using the method AHP method. The AHP method had pros to support group decision making through accord by calculating the geometric mean of the individual pairwise comparisons depicts in Table 4. Criteria having negative impact, uses reciprocal value.
The consistency ratio (CR) for the pairwise comparisons was calculated to be 0.0332.
This matrix can be processed mathematically, the AHP derives priorities for the alternatives with respect to reliability. Priorities are sized by their relative strengths, derived from the judgment of the judgment makers as entered into the matrix. These can also be calculated by hand, or with a spreadsheet, or by using specialized AHP software. The same procedure can be used to calculate the weight to the matrices for Bandwidth, Completion time and Cost by the judgment maker for comparisons as shown in (Tables 5-7).
The consistency ratio (CR) for the pairwise comparisons was calculated to be 0.0739.
The consistency ratio (CR) for the pairwise comparisons was calculated to be 0.074.
The consistency ratio (CR) for the pairwise comparisons was calculated to be 0.0559.
3.1. Criteria versus the Goal
As the judgement makers have evaluated the alternatives to their strength in satisfying the criteria, they will now evaluate the criteria with their importance to reach goal. In this case, the judgment makers have agreed on the following relative weights for the various pairs of Criteria are depicted in (Table 8).
The consistency ratio (CR) for the pairwise comparisons was calculated to be 0.0078.
Table 3. Reliability comparison.
Table 4. Reliability.
Table 5. Bandwidth.
Table 6. Completion time.
Table 7. Cost.
Table 8. Priorities of all criteria goal.
From this decision, Reliability, the highest ranked Criterion to Goal, is about twice as important to the goal as the second highest ranked Criterion, Bandwidth. Similarly, Bandwidth is about twice as important as Cost, which in turn is about twice as important as Completion time as depicts in (Table 9).
Pairwise comparison of four components requires six separate comparisons, while for three components require three. The above refers pairwise comparisons of the four components require a larger matrix. This method has a cons in a cloud computing environment as the number of pairwise comparisons to be made, may become very large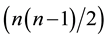
3.2. Final Multi Criteria Priorities Synthesis (MPS)
As we have known the priorities of Criteria to Goal, and the priorities of Alternatives Criteria, we can conveniently calculate the priorities of Alternatives Goal as depicts in (Table 10).
Column X depicts priorities of alternatives Criteria. Column Y depict priority criteria to goal. Column Z depict product of two, which is global priority of each alternative to goal. Overall priorities for all alternatives.
Consequent upon the AHP result, the Cloud app (CA) that can process two or more kinds has the highest overall priority of 0.59 in reaching the goal. The Desktop app with an overall priority of 0.25 is second while the Web app at 0.15 overall priority is third. However, results from (Table 11) depict that the WA has the highest priority of 0.012 in terms of Scalability. The CA has the highest priorities of 0.32, 0.10, and 0.009 in terms of reliability, completion time, and cost respectively to emerge the most applications.
Table 9. Criteria to goal.
Table 10. Calculation of alternative goal.
Table 11. Overall priorities for all alternatives.
4. Conclusion
This paper discusses the result to identify an achievable automation application, and the content should break down to task level. We have added attributes such as the reliability, bandwidth, completion time and cost level analysis during the application prioritization but still other attributes are not included. This analysis can help to re-prioritize for new attributes that are not considered. The proposed framework for the AHP approach will serve as a useful tool for judgment makers to value the range of performance issues that need to be considered when making complex decisions concerning applications. Moreover, the AHP hierarchical structure in this paper presents the well-balanced multi criteria priorities synthesis of various applications factors that must be judged by users for more competition. The AHP is an excellent approach for evaluation intangible concerns. Above case study depicts that CA is better in terms of reliability, completion time and cost with respect to WA which is better for scalability. In future these applications will play a vital role in terms of above mention agile resources at data centers.
Cite this paper
AvtarSingh,KamleshDutta, (2015) Apply AHP for Resource Allocation Problem in Cloud. Journal of Computer and Communications,03,13-21. doi: 10.4236/jcc.2015.310002
References
- 1. Mell, P. and Grance, T. (2011) The NIST Definition of Cloud Computing. Special Publication 800-145.
- 2. Hayes, B. (2008) Cloud Computing. Communications of the ACM, 51, 9-11.
http://dx.doi.org/10.1145/1364782.1364786 - 3. Buyya, R., Yeo, C.S., Srikumar, V., James, B. and Ivona, B. (2009) Cloud Computing and Emerging IT Platforms: Vision, Hype, and Reality for Delivering Computing as the 5th Utility. Future Generation Computer Systems, 25, 599-616.
http://dx.doi.org/10.1016/j.future.2008.12.001 - 4. Buyya, R., Broberg, J. and Goscinski, A. (2011) Cloud Computing: Principle and Paradigm. John Wiley& Sons, Hoboken.
- 5. Armbrust, M., Fox, A., Griffith, R., Joseph, A., Katz, R., Konwinski, A. and Zaharia, M. (2009) Above the Clouds: A Berkeley View of Cloud Computing. Technical Report, University of California at Berkeley.
- 6. Chieu, T.C., Mohindra, A., Alexei, A., Karve, A.A. and Segal, A.A. (2009) Dynamic Scaling of Web Applications in a Virtualized Cloud Computing Environment. Proceedings of the IEEE International Conference on e-Business Engineering, Macau, 21-23 October 2009, 281-286.
http://dx.doi.org/10.1109/icebe.2009.45 - 7. Martens, B. and Teuteberg, F. (2012) Decision-Making in Cloud Computing Environments: A Cost and Risk Based Approach. Information Systems Frontiers, 14, 871-893.
http://dx.doi.org/10.1007/s10796-011-9317-x - 8. Atas, G. and Gungor, V.C. (2014) Performance Evaluation of Cloud Computing Platforms Using Statistical Methods. Computers and Electrical Engineering, 40, 1636-1649.
http://dx.doi.org/10.1016/j.compeleceng.2014.03.017 - 9. Triantaphyllou, E. and Mann, S.H. (1995) Using the Analytic Hierarchy Process for Decision Making in Engineering Applications: Some Challenges. International Journal of Industrial Engineering: Applications and Practice, 2, 35-44.
- 10. Saaty, T.L. (1990) How to Make a Decision: The Analytic Hierarchy Process. European Journal of Operational Research, 48, 9-26.
http://dx.doi.org/10.1016/0377-2217(90)90057-I - 11. Saaty, T.L. (2003) Decision-Making with the AHP: Why Is the Principal Eigenvector Necessary. European Journal of Operational Research, 145, 85-89.
http://dx.doi.org/10.1016/S0377-2217(02)00227-8 - 12. Ergu, D., Kou, G., Peng, Y., Shi, Y. and Shi, Y. (2011) The Analytic Hierarchy Process: Task Scheduling and Resource Allocation in Cloud Computing Environment. The Journal of Supercomputing, 213, 246-259.
- 13. Garg, S.K., Versteeg, S. and Buyya, R. (2013) A Framework for Ranking of Cloud Computing Services. Future Generation Computer Systems, 29, 1012-1023.
http://dx.doi.org/10.1016/j.future.2012.06.006 - 14. Cao, D., Leung, L.C. and Law, J.S. (2008) Modifying Inconsistent Comparison Matrix in Analytic Hierarchy Process: A Heuristic Approach. Journal of Decision Support System, 44, 944-953.
http://dx.doi.org/10.1016/j.dss.2007.11.002 - 15. Carlucci, D. and Schiuma, G. (2007) Knowledge Assets Value Creation Map Assessing Knowledge Assets Value Drivers Using AHP. Expert Systems with Applications, 32, 814-821.
http://dx.doi.org/10.1016/j.eswa.2006.01.046 - 16. Godse, M. and Mulik, S. (2009) An Approach for Selecting Software-as-a-Service (SaaS) Product. Proceedings of the IEEE International Conference on Cloud Computing, Bangalore, 21-25 September 2009, 155-158.
http://dx.doi.org/10.1109/cloud.2009.74 - 17. Saaty, T.L. (1977) A Scaling Method for Priorities in Hierarchical Structures. Journal of Mathematical Psychology, 15, 234-281.
http://dx.doi.org/10.1016/0022-2496(77)90033-5 - 18. Rao, R.V. (2013) Decision Making in the Manufacturing Environment Using Graph Theory and Fuzzy Multiple Attribute Decision Making Methods. Springer Series in Advanced Manufacturing, Springer Verlag, London.
- 19. Karapetrovic, S. and Rosenbloom, E.S. (1999) A Quality Control Approach to Consistency Paradoxes in AHP. European Journal of Operational Research, 119, 704-718.
- 20. Gao, W. and Kang, F. (2012) Cloud Simulation Resource Scheduling Algorithm Based on Multi-Dimension Quality of Service. Information Technology Journal, 11, 94-101.
http://dx.doi.org/10.3923/itj.2012.94.101