Journal of Computer and Communications
Vol.2 No.10(2014), Article
ID:48815,8
pages
DOI:10.4236/jcc.2014.210002
The Solution of Nonlinear Equations via the Method of Hurwitz-Radon Matrices
Dariusz Jacek Jakóbczak
Department of Electronics and Computer Science, Technical University of Koszalin, Koszalin, Poland
Email: djakob@ie.tu.koszalin.pl
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 May 2014; revised 10 June 2014; accepted 5 July 2014
ABSTRACT
Image analysis and computer vision are interested in suitable methods to solve the nonlinear equations. Coordinate  for
for  is crucial because each equation can be transformed into
is crucial because each equation can be transformed into . A novel method of Hurwitz-Radon Matrices (MHR) can be used in approximation of a root of function in the plane. The paper contains a way of data approximation via MHR method to solve any equation. Proposed method is based on the family of Hurwitz-Radon (HR) matrices. The matrices are skew-symmetric and possess columns composed of orthogonal vectors. The operator of Hurwitz-Radon (OHR), built from these matrices, is described. Two-dimensional data are represented by discrete set of curve
. A novel method of Hurwitz-Radon Matrices (MHR) can be used in approximation of a root of function in the plane. The paper contains a way of data approximation via MHR method to solve any equation. Proposed method is based on the family of Hurwitz-Radon (HR) matrices. The matrices are skew-symmetric and possess columns composed of orthogonal vectors. The operator of Hurwitz-Radon (OHR), built from these matrices, is described. Two-dimensional data are represented by discrete set of curve 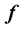 points. It is shown how to create the orthogonal OHR operator and how to use it in a process of data interpolation. MHR method is interpolating the curve point by point without using any formula or function.
points. It is shown how to create the orthogonal OHR operator and how to use it in a process of data interpolation. MHR method is interpolating the curve point by point without using any formula or function.
Keywords:Image Analysis, Nonlinear Equation, Root of Function, Curve Interpolation, Hurwitz-Radon Matrices

1. Introduction
A significant problem in computer vision and image analysis [1] is to solve any nonlinear equation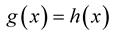 . This means the issue of approximation
. This means the issue of approximation  in equation
in equation  where
where . Two-dimensional data can be treated as points on the curve. Many numerical methods for nonlinear equations are known as iterative methods: bisection, regula falsi, Newton’s method (also called as the Newton-Raphson method), Steffensen’s method, Brent’s method, Broyden’s method, fixed-point iterations, inverse interpolation and the secant method [2] . These methods can be used for any function, but sometimes there are troubles. For example in Newton’s method we may found difficulties in calculating derivative of a function or troubles with bad starting point of iteration. Generally iterative methods need many assumptions about function (monotonicity, convexity, derivative, starting point). Some methods are used only for polynomials (Muller’s, Laguerre’s, Bairstow’s, Jenkins-Traub’s methods). Nonlinear systems are still opened for researchers [3] .
. Two-dimensional data can be treated as points on the curve. Many numerical methods for nonlinear equations are known as iterative methods: bisection, regula falsi, Newton’s method (also called as the Newton-Raphson method), Steffensen’s method, Brent’s method, Broyden’s method, fixed-point iterations, inverse interpolation and the secant method [2] . These methods can be used for any function, but sometimes there are troubles. For example in Newton’s method we may found difficulties in calculating derivative of a function or troubles with bad starting point of iteration. Generally iterative methods need many assumptions about function (monotonicity, convexity, derivative, starting point). Some methods are used only for polynomials (Muller’s, Laguerre’s, Bairstow’s, Jenkins-Traub’s methods). Nonlinear systems are still opened for researchers [3] .
This paper is dealing with novel method of root’s approximation by using a family of Hurwitz-Radon matrices. Method of Hurwitz-Radon Matrices (MHR) does not need any assumption about function. The only information about curve is the set of at least five interpolation nodes and a zero of the function between two of them. Proposed method of Hurwitz-Radon Matrices (MHR) is used in data interpolation and then calculations to solve the nonlinear equation are introduced. MHR connects two significant problems in mathematics and computer sciences: interpolation of the function and the solution of nonlinear equation [4] . MHR method uses two-dimensional data for knowledge representation [5] and computational foundations [6] . Also medicine [7] , industry and manufacturing are looking for the methods connected with geometry of the curves [8] . So suitable data representation and precise solving of any equation [9] are the key factors in many applications of artificial intelligence and numerical methods [10] .
2. Assumptions for the Solution
Each nonlinear equation is represented by  and succeeding points
and succeeding points  of function
of function 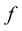 (interpolation nodes) as follows in proposed MHR method:
(interpolation nodes) as follows in proposed MHR method:
1. first node 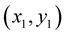 and last node
and last node 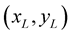 must fulfill a condition
must fulfill a condition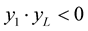 ;
;
2. at least three nodes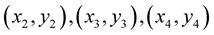 , for example equidistant between first and last node, have to be calculated (for
, for example equidistant between first and last node, have to be calculated (for![]() ) if MHR method is used with matrices of dimension
) if MHR method is used with matrices of dimension![]() .
.
Condition 1 is well known in numerical methods for existing a zero of the function. Condition 2 is connected with important features of MHR method: MHR version with matrices of dimension ![]() (called MHR-2) needs at least five nodes (for
(called MHR-2) needs at least five nodes (for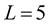 ), MHR version with matrices of dimension
), MHR version with matrices of dimension ![]() (called MHR-4) needs at least nine nodes (for
(called MHR-4) needs at least nine nodes (for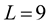 ) and MHR version with matrices of dimension
) and MHR version with matrices of dimension ![]() (called MHR-8) needs at least 17 nodes (for
(called MHR-8) needs at least 17 nodes (for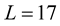 ).
).
Figure 1 presents the graph of function 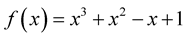 with nodes: first
with nodes: first 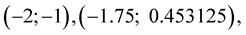
 and last
and last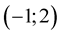 . All five nodes are applied in MHR calculations, but a root of function is searched only between nodes
. All five nodes are applied in MHR calculations, but a root of function is searched only between nodes  and
and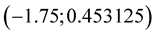 . The approximation of a zero point of the function is possible using novel MHR method.
. The approximation of a zero point of the function is possible using novel MHR method.
3. Reconstruction of the Graph Points
The key question exists in many branches of science: is it possible to find a method of nonlinear equation solution without iterations of numerical methods [11] ? This paper aims at giving the positive answer to this question. Method of Hurwitz-Radon Matrices (MHR), described in this paper, is computing points between two successive nodes for searching a root of the function. The curve or function in MHR method is parameterized for real number 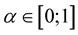 in the range of two successive interpolation nodes.
in the range of two successive interpolation nodes.
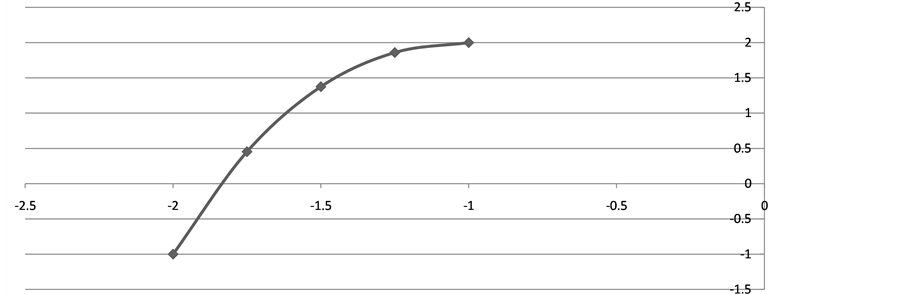
Figure 1. Five nodes of function and a root between first and second node (MS Excel graph).
3.1. The Operator of Hurwitz-Radon
Adolf Hurwitz (1859-1919) and Johann Radon (1887-1956) published the papers about specific class of matrices in 1923, working on the problem of quadratic forms. Matrices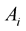 ,
,  satisfying
satisfying

are called a family of Hurwitz-Radon matrices. A family of Hurwitz-Radon (HR) matrices has important features [12] : HR matrices are skew-symmetric 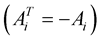 and reverse matrices are easy to find
and reverse matrices are easy to find . Only for dimension
. Only for dimension 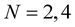 or 8 the family of HR matrices consists of
or 8 the family of HR matrices consists of 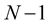 matrices. For
matrices. For 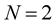 there is one matrix:
there is one matrix:
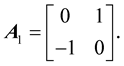
For 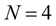 there are three HR matrices with integer entries:
there are three HR matrices with integer entries:
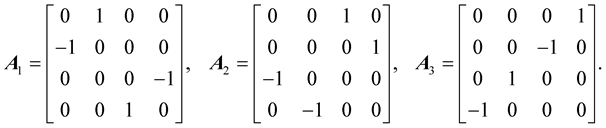
For  we have seven HR matrices with elements 0, ±1. So far HR matrices are applied in electronics [13] : in Space-Time Block Coding (STBC) and orthogonal design [14] , also in signal processing [15] and Hamiltonian Neural Nets [16] .
we have seven HR matrices with elements 0, ±1. So far HR matrices are applied in electronics [13] : in Space-Time Block Coding (STBC) and orthogonal design [14] , also in signal processing [15] and Hamiltonian Neural Nets [16] .
If one curve is described by a set of following points  then HR matrices combined with the identity matrix IN are used to build the orthogonal and discrete Hurwitz-Radon Operator (OHR). For nodes
then HR matrices combined with the identity matrix IN are used to build the orthogonal and discrete Hurwitz-Radon Operator (OHR). For nodes  and
and  OHR
OHR 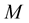 of dimension
of dimension  is constructed:
is constructed:
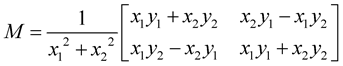 . (1)
. (1)
For nodes  and
and 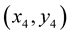 OHR of dimension
OHR of dimension  is constructed:
is constructed:
 (2)
(2)
where
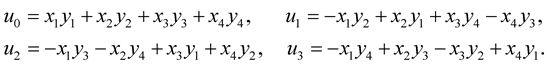
For nodes 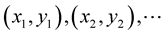 and
and 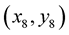 OHR of dimension
OHR of dimension 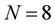 is built [17] similarly as (1) and (2):
is built [17] similarly as (1) and (2):
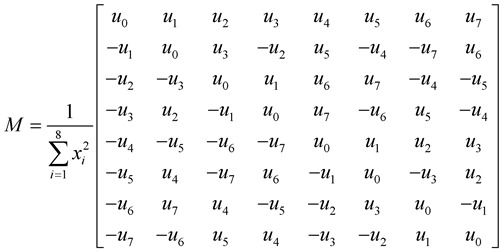 (3)
(3)
where
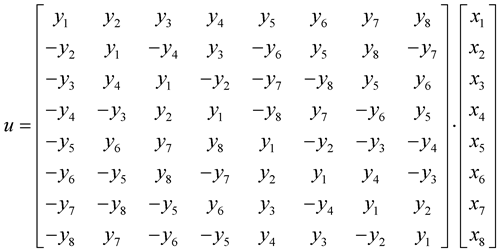 (4)
(4)
The components of the vector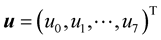 , appearing in the matrix
, appearing in the matrix 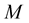 (3), are defined by (4) in the similar way to (1) and (2) but in terms of the coordinates of the above 8 nodes. Note that OHR operators
(3), are defined by (4) in the similar way to (1) and (2) but in terms of the coordinates of the above 8 nodes. Note that OHR operators 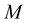 (1)-(3) satisfy the condition of interpolation
(1)-(3) satisfy the condition of interpolation
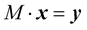 (5)
(5)
For 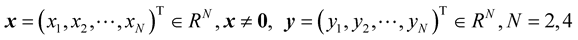 or 8.
or 8.
3.2. Points Interpolation by MHR
Key question looks as follows: how can we compute coordinates of points settled between the interpolation nodes [18] ? The answer is connected with novel MHR method [19] . On a segment of a line every number “ ” situated between “
” situated between “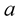 ” and “
” and “ ” is described by a linear (convex) combination
” is described by a linear (convex) combination 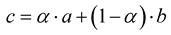 for
for
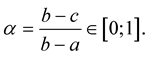 (6)
(6)
The average OHR operator 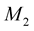 of dimension
of dimension 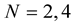 or 8 is constructed as follows:
or 8 is constructed as follows:
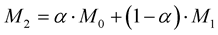 (7)
(7)
with the operator 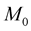 built (1)-(3) by “odd” nodes
built (1)-(3) by “odd” nodes 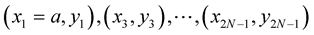 and
and  built (1)-(3) by “even” nodes
built (1)-(3) by “even” nodes . Having the operator
. Having the operator 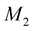 it is possible to reconstruct the second coordinates of points
it is possible to reconstruct the second coordinates of points  in terms of the vector
in terms of the vector  defined with
defined with
 (8)
(8)
as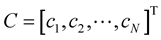 . The required formula is similar to (5):
. The required formula is similar to (5):
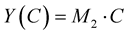 (9)
(9)
in which components of vector  give the second coordinate of the points
give the second coordinate of the points 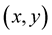 corresponding to the first coordinate, given in terms of components of the vector
corresponding to the first coordinate, given in terms of components of the vector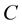 .
.
Calculations of unknown coordinates for curve points using (6)-(9) are called by author the method of Hurwitz-Radon Matrices (MHR) [20] . Here is the application of MHR method (Figure 2) for function 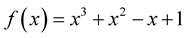 with nodes as Figure 1 and computed 99 points between each pair of nodes
with nodes as Figure 1 and computed 99 points between each pair of nodes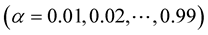 .
.
Solving the equation 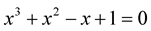 via MHR interpolation, as it was said under Figure 1, we search a root of the function only between nodes
via MHR interpolation, as it was said under Figure 1, we search a root of the function only between nodes 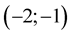 and
and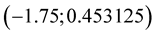 . Points calculated between other pairs of nodes are useless in the process of root approximation and they don’t have to be computed. Considering calculated points between nodes
. Points calculated between other pairs of nodes are useless in the process of root approximation and they don’t have to be computed. Considering calculated points between nodes 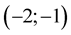 and
and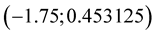 , second coordinate is near zero at
, second coordinate is near zero at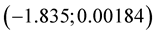 . Solution of equation
. Solution of equation 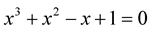 via MHR-2 method is approximated by
via MHR-2 method is approximated by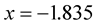 . True value is
. True value is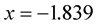 .
.
The same equation for nodes  and
and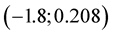 , solved by MHR-2, gives better result
, solved by MHR-2, gives better result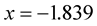 . So shorter distance between first and last node is of course
. So shorter distance between first and last node is of course
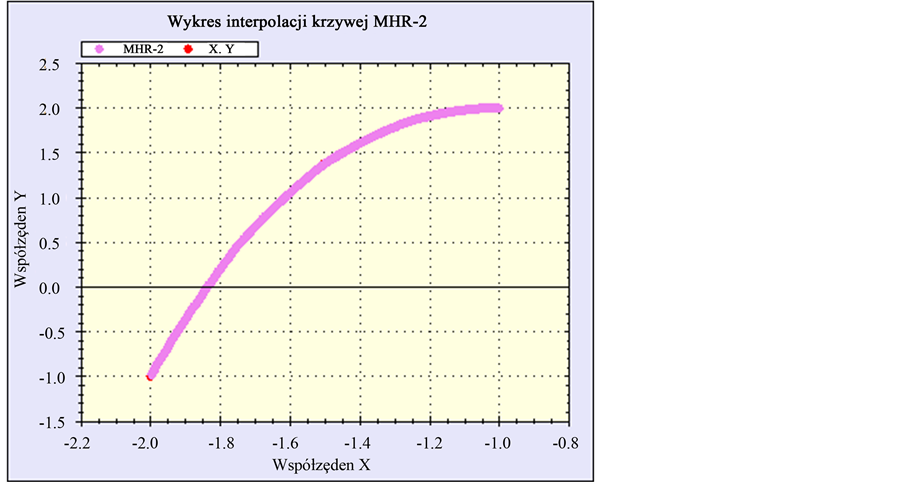
Figure 2. Function 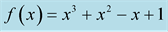 with 396 interpolated points using MHR-2 method.
with 396 interpolated points using MHR-2 method.
very important feature.
4. Nonlinear Equations Solved via MHR
Example 1 MHR calculations are done for function  with nodes:
with nodes: 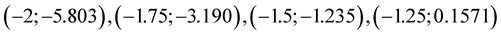 and
and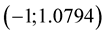 . So a root of this function is situated between 3rd and 4th node. MHR-2 interpolation gives the graph of function (Figure 3):
. So a root of this function is situated between 3rd and 4th node. MHR-2 interpolation gives the graph of function (Figure 3):
Considering points between nodes  and
and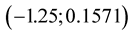 , coordinate y is near zero at
, coordinate y is near zero at . Solution of equation
. Solution of equation 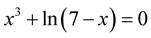 via MHR method is approximated by
via MHR method is approximated by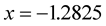 . True value is hardly approximated (even for MathCad) by
. True value is hardly approximated (even for MathCad) by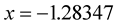 .
.
Example 2 MHR calculations are completed for function 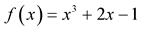 with nodes:
with nodes: 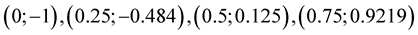 and
and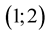 . So a zero of this function is situated between 2nd and 3rd node. MHR-2 computes the graph of function (Figure 4).
. So a zero of this function is situated between 2nd and 3rd node. MHR-2 computes the graph of function (Figure 4).
Considering points between nodes 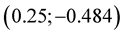 and
and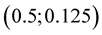 , coordinate y is near zero at
, coordinate y is near zero at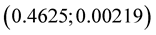 . Solution of equation
. Solution of equation 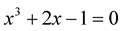 via MHR-2 is approximated by
via MHR-2 is approximated by . The only one real solution of this equation is
. The only one real solution of this equation is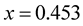 .
.
Now MHR calculations are done for the same equation 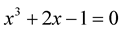 with seven nodes between
with seven nodes between  and
and 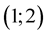 for
for 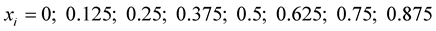 and 1. The solution is approximated by MHR-4 method with nine nodes. MHR-4 interpolation gives the graph of function (Figure 5).
and 1. The solution is approximated by MHR-4 method with nine nodes. MHR-4 interpolation gives the graph of function (Figure 5).
Considering points between nodes and
and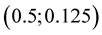 , coordinate y is near zero at
, coordinate y is near zero at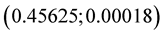 . Solution of equation
. Solution of equation 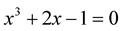 via MHR-4 is approximated by
via MHR-4 is approximated by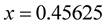 . This is better result than MHR-2: greater number of nodes (with the same distance between first and last) means better approximation. And seventeen nodes in MHR-8 guarantee more precise results then MHR-4.
. This is better result than MHR-2: greater number of nodes (with the same distance between first and last) means better approximation. And seventeen nodes in MHR-8 guarantee more precise results then MHR-4.
Example 3 MHR calculations are done for equation  with nodes:
with nodes: 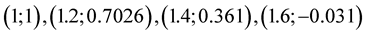 and
and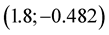 . MHR-2 gives the graph of function (Figure 6).
. MHR-2 gives the graph of function (Figure 6).
Considering points between nodes 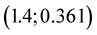 and
and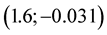 , second coordinate is near zero at
, second coordinate is near zero at . Solution of equation
. Solution of equation 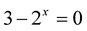 via MHR-2 method is approximated by
via MHR-2 method is approximated by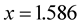 . Pre-
. Pre-

Figure 3. Function 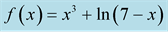 with 396 interpolated points using MHR-2.
with 396 interpolated points using MHR-2.
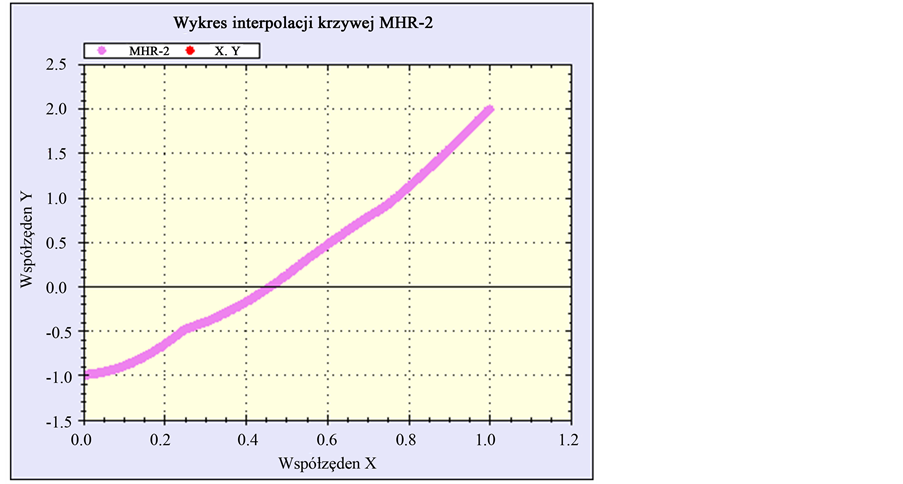
Figure 4. Function  with 396 interpolated points using MHR-2.
with 396 interpolated points using MHR-2.
cise solution  is approximated by 1.585.
is approximated by 1.585.
Interpolated values, calculated by MHR method, are applied in the process of solving the nonlinear equations. Shorter distance between first and last node or greater number of nodes guarantee better approximation. Approximated solutions of nonlinear equations are used in many branches of computer sciences. MHR joins two important problems: interpolation of the function with the solution of nonlinear equation.
5. Conclusions
The method of Hurwitz-Radon Matrices leads to curve interpolation [21] and approximation of nonlinear equation solution depending on the number and location of nodes. No characteristic features of function is important
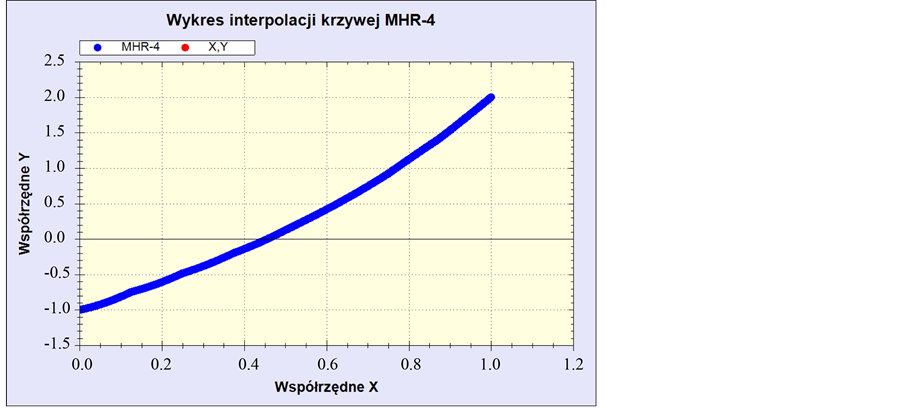
Figure 5. Function 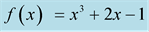 with interpolated points using MHR- 4 method with 9 nodes.
with interpolated points using MHR- 4 method with 9 nodes.
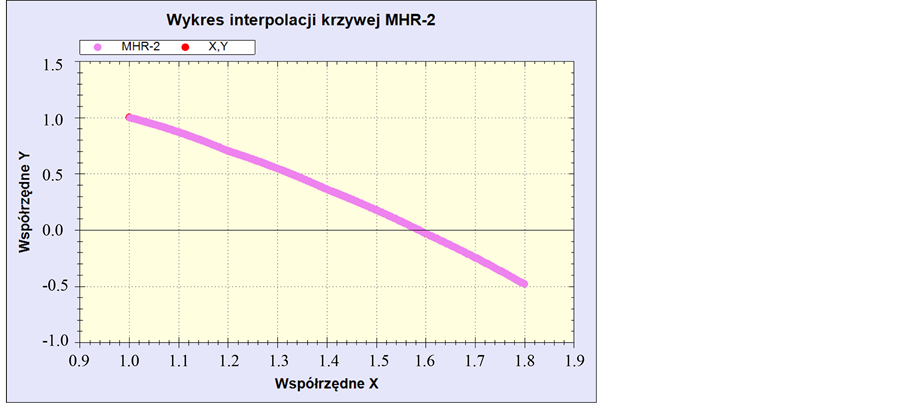
Figure 6. Function 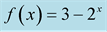 with 396 interpolated points using MHR- 2 method with 5 nodes.
with 396 interpolated points using MHR- 2 method with 5 nodes.
in MHR method: polynomial or not, monotonicity, convexity, derivative, starting point. These features are very significant for iterative numerical methods. MHR method gives the possibility of reconstruction a curve and searching for a root of the function. The only condition is to have a set of nodes according to assumptions in MHR method. The features of MHR method: accuracy of the equation solution depends on the number of nodes and the distance between first and last node (MHR-4 is more precise than MHR-2 and MHR-8 is more precise than MHR-4); interpolation of a curve consists of 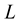 points is connected with the computational cost of rank
points is connected with the computational cost of rank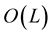 ; MHR is a well-conditioned method (orthogonal matrices); MHR is not an affine interpolation [22] .
; MHR is a well-conditioned method (orthogonal matrices); MHR is not an affine interpolation [22] .
Future works are connected with: computing the interpolation error, implementation of MHR in object recognition [23] , MHR extrapolation method [24] and curve parameterization [25] .
References
- Ballard, D.H. (1982) Computer Vision. Prentice Hall, New York.
- Yang, W.Y., Cao, W., Chung, T.-S. and Morris, J. (2005) Applied Numerical Methods Using MATLAB®. John Wiley & Sons, New York. http://dx.doi.org/10.1002/0471705195
- Khalil, H.K. (2001) Nonlinear Systems. Prentice Hall, New York.
- Kelley, C.T. (1995) Iterative Methods for Linear and Nonlinear Equations. Society for Industrial and Applied Mathematics, Philadelphia.
http://dx.doi.org/10.1137/1.9781611970944 - Markman, A.B. (1998) Knowledge Representation. Lawrence Erlbaum Associates, Mahwah.
- Sowa, J.F. (2000) Knowledge Representation: Logical, Philosophical and Computational Foundations. Brooks/Cole, New York.
- Soussen, C. and Mohammad-Djafari, A. (2004) Polygonal and Polyhedral Contour Reconstruction in Computed Tomography. IEEE Transactions on Image Processing, 11, 1507-1523.
http://dx.doi.org/10.1109/TIP.2004.836159 - Tang, K. (2005) Geometric Optimization Algorithms in Manufacturing. Computer-Aided Design & Applications, 2, 747-757. http://dx.doi.org/10.1080/16864360.2005.10738338
- Kozera, R. (2004) Curve Modeling via Interpolation Based on Multidimensional Reduced Data. Silesian University of Technology Press, Gliwice.
- Dahlquist, G. and Bjoerck, A. (1974) Numerical Methods. Prentice Hall, New York.
- Ralston, A. (1965) A First Course in Numerical Analysis. McGraw-Hill Book Company, New York.
- Eckmann, B. (1999) Topology, Algebra, Analysis-Relations and Missing Links. Notices of the American Mathematical Society, 5, 520-527.
- Citko, W., Jakóbczak, D. and Sieńko, W. (2005) On Hurwitz-Radon Matrices Based Signal Processing. Workshop Signal Processing at Poznan University of Technology, Poznan.
- Tarokh, V., Jafarkhani, H. and Calderbank, R. (1999) Space-Time Block Codes from Orthogonal Designs. IEEE Transactions on Information Theory, 5, 1456-1467.
http://dx.doi.org/10.1109/18.771146 - Sieńko, W., Citko, W. and Wilamowski, B. (2002) Hamiltonian Neural Nets as a Universal Signal Processor. 28th Annual Conference of the IEEE Industrial Electronics Society IECON, Sevilla.
- Sieńko, W. and Citko, W. (2002) Hamiltonian Neural Net Based Signal Processing. The International Conference on Signal and Electronic System ICSES, Wroclaw.
- Jakóbczak, D. (2007) 2D and 3D Image Modeling Using Hurwitz-Radon Matrices. Polish Journal of Environmental Studies, 16, 104-107.
- Jakóbczak, D. (2010) Shape Representation and Shape Coefficients via Method of Hurwitz-Radon Matrices. In: Computer Vision and Graphics, in: Lecture Notes in Computer Science, 6374, 411-419.
- Jakóbczak, D. (2009) Curve Interpolation Using Hurwitz-Radon Matrices. Polish Journal of Environmental Studies, 18, 126-130.
- Jakóbczak, D. (2010) Application of Hurwitz-Radon Matrices in Shape Representation. In: Banaszak, Z. and Swic, A., Eds., Applied Computer Science: Modelling of Production Processes, Lublin University of Technology Press, Lublin, 63-74.
- Jakóbczak, D. (2010) Object Modeling Using Method of Hurwitz-Radon Matrices of Rank k. In: Wolski, W. and Borawski, M., Eds., Computer Graphics: Selected Issues, University of Szczecin Press, Szczecin, 79-90.
- Jakóbczak, D. (2010) Implementation of Hurwitz-Radon Matrices in Shape Representation. In: Choras, R.S., Ed., Advances in Intelligent and Soft Computing, Vol. 84, Image Processing and Communications Challenges, 39-50.
- Jakóbczak, D. (2011) Object Recognition via Contour Points Reconstruction Using Hurwitz-Radon Matrices. In: Józefczyk, J. and Orski, D., Eds., Knowledge-Based Intelligent System Advancements: Systemic and Cybernetic Approaches, IGI Global, Hershey, 87-107.
- Jakóbczak, D. (2011) Data Extrapolation and Decision Making via Method of Hurwitz-Radon Matrices. In: Jedrzejowicz, P., Thanh Nguyen, N. and Hoang, K., Eds., Computational Collective Intelligence, Technologies and Applications, Lecture Notes in Computer Science, Vol. 6922, 173-182.
- Jakóbczak, D. (2011) Curve Parameterization and Curvature via Method of Hurwitz-Radon Matrices. Image Processing & Communications, 16, 49-56.

