Journal of Applied Mathematics and Physics
Vol.07 No.01(2019), Article ID:89766,10 pages
10.4236/jamp.2019.71002
New Soliton Solutions to the Initial Value Problem for the Two-Component Short Pulse Equation
Yan Luo
College of Science, University of Shanghai for Science and Technology, Shanghai, China

Copyright © 2019 by author(s) and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: December 5, 2018; Accepted: January 6, 2019; Published: January 9, 2019
ABSTRACT
We formulate a matrix Riemann-Hilbert problem to the initial value problem for the two-component system proposed by Matsuno. By solving the associated Riemann-Hilbert problem, we can get the soliton solutions of the two-component system. One and two soliton solutions are investigated in detail.
Keywords:
Riemann-Hilbert Problem, Two-Component Short Pulse Equation, Soliton Solutions

1. Introduction
The SP (short pulse) equation
(1)
where represents the magnitude of the electric field and subscripts x and t appended to u denote partial differentiation, has been proposed as a model equation describing the propagation of ultrashort optical pulses in nonlinear media [1] . A numerical analysis shows that as the pulse length shortens, the SP equation becomes a better approximation to the solution of the Maxwell equation when compared with the prediction of the NLS equation [2] . Then Matsuno proposed a novel multi-component generalization of the SP equation [3] , which generalizes the SP equation describing the propagation of ultra-short pulses in optical fibers. Here we consider the multi-component system [3] .
(2)
with reduced two-component short pulse system if letting n = 2, which given by
(3)
where and . Then we make the transformation and this system can be written as
(4)
We named Equation (4) as 2SPE (two-component system). Obviously if we put , then 2SPE reduces to the SP equation. The integrability, soliton solutions, and other features of Equation (1) and Equation (4) common to the completely integrable PDEs (partial differential equations) have been studied from various points of view [3] [4] [5] [6] . And the semi-discretization of a multi-component SP equation was studied in [7] , super extensions in [8] .
Here, in this paper, we consider the initial value problem for the 2SPE (4) with the initial value data , and denotes the Schwartz space. The present paper is devoted to analyze the IVP (initial value problem) for the Equation (4) by Riemann-Hilbert approach.
Organization of the paper: In Section 2, we formulate the associated Riemann-Hilbert problem by performing the similar spectral analysis to the Equation (4) as [9] . In Section 3, to obtain the soliton solutions of the Equation (4), we need analyze the residue conditions of the Riemann-Hilbert problem. Especially, the one and two soliton solutions are investigated in detail.
2. Riemann-Hilbert Problem for the Two-Component System
The 2SPE admits a WKI (Wadati-Konno-Ichikawa)-type Lax pair as follow:
(5)
where
(6)
with
(7)
2.1. Spectral Analysis for k = 0
Introducing
(8)
Then we can get the Lax pair of
(9)
where
(10)
We define two eigenfunctions of
(11)
Proposition 1: The functions are bounded and analytic as:
(12)
where means that the 1-th column and 2-th column of are bounded and analytic in and , respectively, and
Proposition 2: The functions have the expansions as:
(13)
2.2. Spectral Analysis for k = ∞
Define
(14)
(15)
where .
Introduce the following transformation:
(16)
where
(17)
(18)
(19)
We find the Lax pair equation of
(20)
where
(21)
(22)
Then, define two eigenfunctions of :
(23)
Proposition 3: The functions are bounded and analytic as:
(24)
Proposition 4: The functions also satisfies
(25)
Proposition 5: (Symmetry property) In this paper, we consider the function and are real-value functions. Then, the eigenfunctions satisfy the following symmetry property:
(26)
2.3. Spectral Function s(k)
The eigenfunctions and are related
(27)
where the matrix is independent of and has the form
(28)
The function and can be computed by
(29)
where means the determinate of matrix X.
Hence, form the analytic properties of the functions , we know that and are analytic in and , respectively.
2.4. The Relation between and
Proposition 6: The functions and are related
(30)
where and .
Proposition 7: The spectral functions and have the following asymptotic behaviors as :
(31)
where .
2.5. The Riemann-Hilbert Problem
Let us define
(32)
Making coordinate transformation
(33)
and defining
(34)
Then, satisfies the Riemann-Hilbert problem as follows:
(35)
(36)
where
(37)
To obtain the solution and of the Equation (4), we need the asymptotic behavior of as ,
(38)
Hence, we can get the solution of Equation (4)
(39)
where
(40)
3. Solitons
In order to get the soliton solutions of 2SPE, we assume that has N simple zero points and has N simple zero points . Then, there exist some constant and such that,
(41)
Thus, according to the above formula we have
(42)
3.1. One Soliton Solution
Take into Equation (42), evaluating at and of the 1-th and 2-th column of , then solving the algebra system for and , we can get
(43)
By the symmetry condition, . And for simplify choosing and , ; b, c and are real constants; denoting , and , then we get one soliton solution
(44)
3.2. Two-Soliton Solutions
Take into Equation (42), we can get
(45)
1)
Letting , and choosing , and denoting and , where , repeating the process of one soliton solution, then we can get the two soliton solutions.
Parameter selection case one: Choosing , , , , where c is an arbitrary constant, we have
(46)
Remark 8: The Result (46) is coincide with the breather-solution of SP equation as [6] , since the parameter chosen satisfies the symmetry condition of SP equation as [9] .
Parameter selection case two: Choosing , , , , then, we can get
(47)
2) Two pure image zeros
If choosing , , , , where , , and denoting , , then letting the parameter be , , , , we have
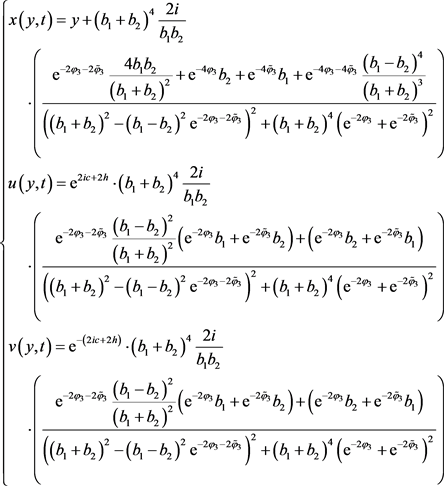 (48)
(48)
Remark 9: To our knowledge, the result (47) and result (48) are new.
4. Conclusion
In this article, we consider IVP for the 2SPE with initial value in Schwartz space. We begin with the Lax pair of 2SPE and then we formulate a Riemann-Hilbert problem in new coordinate (y, t), which implies that we can get the parametric form of soliton solutions in terms of the solution of the associated Riemann-Hilbert problem. After that, we can get the soliton solution by analyzing the residue condition of the Riemann-Hilbert problem. Last we obtain the soliton solutions, in particular the new breather-solution (47) and two soliton solution (48) were obtained.
Conflicts of Interest
The author declares no conflicts of interest regarding the publication of this paper.
Cite this paper
Luo, Y. (2019) New Soliton Solutions to the Initial Value Problem for the Two-Component Short Pulse Equation. Journal of Applied Mathematics and Physics, 7, 13-22. https://doi.org/10.4236/jamp.2019.71002
References
- 1. Schafer, T. and Wayne, C.E. (2004) Propagation of Ultra-Short Optical Pulses in Cubic Nonlinear Media. Physica D: Nonlinear Phenomena, 196, 90-105.https://doi.org/10.1016/j.physd.2004.04.007
- 2. Chung, Y., Jones, C.K.R.T., Schafer, T. and Wayne, C.E. (2004) Ultra-Short Pulses in Linear and Nonlinear Media. Nonlinearity, 18, 1351-1374. https://doi.org/10.1088/0951-7715/18/3/021
- 3. Matsuno, Y. (2011) A Novel Multi-Component Generalization of the Short Pulse Equation and Its Multisoliton Solutions. Journal of Mathematical Physics, 52, Article ID: 123702. https://doi.org/10.1063/1.3664904
- 4. Sakovich, A. and Sakovich, S. (2005) The Short Pulse Equation Is Integrable. Journal of the Physical Society of Japan, 74, 239-241. https://doi.org/10.1143/JPSJ.74.239
- 5. Brunelli, J.C. (2006) The Bi-Hamiltonian Structure of the Short Pulse Equation. Physics Letters A, 353, 475-478. https://doi.org/10.1016/j.physleta.2006.01.009
- 6. Sakovich, A. and Sakovich, S. (2006) Solitary Wave Solutions of the Short Pulse Equation. Journal of Physics A General Physics, 39, L361-L367.
- 7. Feng, B.F., Maruno, K.I. and Ohta, Y. (2010) Integrable Discretizations of the Short Pulse Equation. Journal of Physics A: Mathematical & Theoretical, 43, 555-557.
- 8. Brunelli, J.C. (2018) Super Extensions of the Short Pulse Equation. Communications in Nonlinear Science & Numerical Simulation, 63, 356-364. https://doi.org/10.1016/j.cnsns.2018.04.001
- 9. Xu, J. (2018) Long-Time Asymptotics for the Short Pulse Equation. Journal of Differential Equations, 265, 3494-3532. https://doi.org/10.1016/j.jde.2018.05.009

