Journal of Applied Mathematics and Physics
Vol.06 No.07(2018), Article ID:85890,7 pages
10.4236/jamp.2018.67118
The Nonexistence of Global Solutions for a Time Fractional Schrödinger Equation with Nonlinear Memory
Yaning Li1*, Quanguo Zhang2
1College of Mathematics & Statistics, Nanjing University of Information Science & Technology, Nanjing, China
2Department of Mathematics, Luoyang Normal University, Luoyang, Henan, China

Copyright © 2018 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: June 7, 2018; Accepted: July 7, 2018; Published: July 10, 2018
ABSTRACT
In this paper, we study the nonexistence of solutions of the following time fractional nonlinear Schrödinger equations with nonlinear memory
where , denotes the principal value of , , , , is a complex-value function, denotes left Riemann-Liouville fractional integrals of order and is the Caputo fractional derivative of order . We obtain that the problem admits no global weak solution when and under different conditions for initial data.
Keywords:
Fractional Schrödinger Equation, Nonexistence, Cauchy Problems, Nonlinear Memory

1. Introduction
This paper is concerned with the nonexistence of solutions to the Cauchy problem for the time fractional nonlinear Schrödinger equations with nonlinear memory
(1)
where , denotes principal value of , , , , is a complex-valued function, , and are real-valued functions. denotes left Riemann-Liouville fractional integrals of order and
.
For the nonlinear Schrödinger equations without gauge invariance (i.e. ),
(2)
Ikeda and Wakasugi [1] and Ikeda and Inui [2] [3] proved blow-up results of solutions for (2) under different conditions for
and .
The main tool they used is test function method. This method is based on rescalings of a compactly support test function to prove blow-up results which is first used by Mitidieri and Pohozaev [4] to show the blow-up results.
Recently, it has been seen that fractional differential equations have better effects in many realistic applications than the classical ones. So, considerable attention has been attracted to time fractional diffusion equation which arises in electromagnetic, acoustic and mechanical phenomena etc. [5] , and is derived from classical diffusion equation by replacing the first-order time derivative by a fractional derivative of order with . Fractional diffusion equation was explicitly applied to physics by Nigmatullin [6] to describe diffusion in media with fractal geometry (special types of porous media). There are many papers about the existence and properties of solutions for fractional differential equation, see for example [7] [8] [9] [10] [11] and the references therein.
For nonlinear time fractional Schrödinger equations (i.e., (1) with ), Zhang, Sun and Li [12] studied the nonexistence of this problem in and proved that the problem admits no global weak solution with suitable initial
data when by using test function method, and also give some
conditions which imply the problem has no global weak solution for every .
In [13] , Cazenave, Dickstein and Weissler considered a class of heat equation with nonlinear memory. They obtained that the solution blows up in finite time and under suitable conditions the solution exists globally. In [14] , using test function method, the authors considered a heat equation with nonlinear memory, they determined Fujita critical exponent of the problem.
Motivated by above results, in present paper, our purpose is to study the nonexistence of global weak solutions of (1) with a condition related to the sign of initial data when
and .
This paper is organized as follows. In Section 2, some preliminaries and the main results are presented. In Section 3, we give proof of the main results.
2. Preliminaries and the Main Results
For convenience of statement, let us present some preliminaries that will be used in next sections.
If , and , then we have the following formula of integration by parts
(3)
We need calculate Caputo fractional derivative of the following function, which will be used in next sections. For given and , if we let
then
(see for example [15] ).
Now, we present the definition of weak solution of (1).
Definition 2.1. Let , and , we call is a weak solution of (1) if
for every with and . Moreover, if can be arbitrarily chosen, then we call u is a global weak solution for of (1).
Denote
,
and .
The following theorems show main result of this paper.
Theorem 2.2. Let . If and satisfies
then problem (1) admits no global weak solution.
Theorem 2.3. If , let . If and satisfies
then problem (1) admits no global weak solution.
3. Proofs of Main Result
In this section, we prove blow-up results and global existence of mild solutions of (1).
Proof of Theorem 2.2. If
,
for the case , we may as well suppose that and . Let such that for , for and . For , we define
Let . Assuming that u is a weak solution of (1), and since , we have
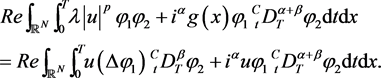
that is
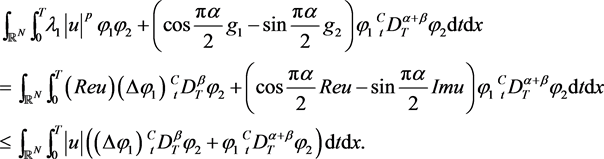 (4)
(4)
Note that
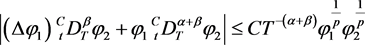 (5)
(5)
for some positive constant C independent of T. Then, by (4), (5) and Hölder inequality, we have

Hence
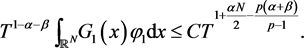
Since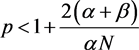 , we have
, we have . Therefore, if the solution of (1) exists globally, then taking
. Therefore, if the solution of (1) exists globally, then taking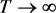 , we obtain
, we obtain
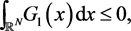
which contradicts with the assumption.
For case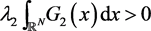 , we have
, we have
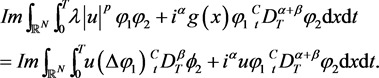
Then by a similar proof as above, we can also obtain a contradiction.
Proof of Theorem 2.3. We only consider the case 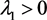 and
and , since other cases can be proved by a similar method. Take
, since other cases can be proved by a similar method. Take 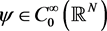 such that
such that
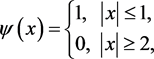
and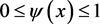 ,
,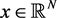 . Let
. Let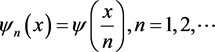 . Suppose that u is a bounded weak solution of (1), taking
. Suppose that u is a bounded weak solution of (1), taking
and define


Since
and
by (6) and dominated convergence theorem, let

Hence, by Jensen’s inequality and (7), we have
Denoting

Thus,
So,

since


assumption. Therefore, if 

Supported
Supported by NSF of China (11626132, 11601216).
Cite this paper
Li, Y.N. and Zhang, Q.G. (2018) The Nonexistence of Global Solutions for a Time Fractional Schrödinger Equation with Nonlinear Memory. Journal of Applied Mathematics and Physics, 6, 1418-1424. https://doi.org/10.4236/jamp.2018.67118
References
- 1. Ikeda, M. and Wakasugi, Y. (2013) Small Data Blow-Up of L2-Solution for the Nonlinear Schrödinger Equation without Gauge Invariance. Differential Integral Equations, 26, 1275-1285.
- 2. Ikeda, M. and Inui, T. (2015) Small Data Blow-Up of L2 or H1-Solution for the Semilinear Schrodinger Equation without Gauge Invariance. Journal of Evolution Equations, 15, 1-11. https://doi.org/10.1007/s00028-015-0273-7
- 3. Ikeda, M. and Inui, T. (2015) Some Non-Existence Results for the Semilinear Schrödinger Equation without Gauge Invariance. Journal of Mathematical Analysis and Applications, 425, 758-773. https://doi.org/10.1016/j.jmaa.2015.01.003
- 4. Mitidieri, E. and Pohozaev, S.I. (2001) A Priori Estimates and Blow-Up of Solutions to Nonlinear Partial Differential Equations and Inequalities. Proceedings of the Steklov Institute of Mathematics, 234, 1-383.
- 5. Mainardi, F. (1994) On the Initial Value Problem for the Fractional Diffusion-Wave Equation. In Rionero, S. and Ruggeri, T., Eds., Waves and Stability in Continuous Media, World Scientific, Singapore, 246-251.
- 6. Nigmatullin, R.R. (1986) The Realization of the Generalized Transfer Equation in a Medium with Fractal Geometry. Physica Status Solidi, 133, 425-430. https://doi.org/10.1002/pssb.2221330150
- 7. Andrade, B. and Viana, A. (2017) On a Fractional Reaction-Diffusion Equation. Zeitschrift für angewandte Mathematik und Physik, 68, 59. https://doi.org/10.1007/s00033-017-0801-0
- 8. Li, Y.N. (2015) Regularity of Mild Solutions for Fractional Abstract Cauchy Problem with Order . Zeitschrift für angewandte Mathematik und Physik, 66, 3283-3298. https://doi.org/10.1007/s00033-015-0577-z
- 9. Li, Y.N., Sun, H.R. and Feng, Z.S. (2016) Fractional Abstract Cauchy Problem with Order . Dynamics of PDE, 13, 155-177.
- 10. Vergara, V. and Zacher, R. (2017) Stability, Instability, and Blowup for Time Fractional and Other Nonlocal in Time Semilinear Subdiffusion Equations. Journal of Evolution Equations, 17, 599-626. https://doi.org/10.1007/s00028-016-0370-2
- 11. Zhang, Q.G. and Sun, H.R. (2015) The Blow-Up and Global Existence of Solutions of Cauchy Problems for a Time Fractional Diffusion Equation. Topological Methods in Nonlinear Analysis, 46, 69-92. https://doi.org/10.12775/TMNA.2015.038
- 12. Zhang, Q.G., Sun, H.R. and Li, Y.N. (2017) The Nonexistence of Global Solutions for a Time Fractional Nonlinear Schrödinger Equation without Gauge Invariance. Applied Mathematics Letters, No. 64, 119-124. https://doi.org/10.1016/j.aml.2016.08.017
- 13. Cazenave, T., Dickstein, F. and Weissler, F.B. (2008) An Equation Whose Fujita Critical Exponent Is Not Given by Scaling. Nonlinear Analysis, 68, 862-874. https://doi.org/10.1016/j.na.2006.11.042
- 14. Fino, A.Z. and Kirane, M. (2012) Qualitative Properties of Solutions to a Time-Space Fractional Evolution Equation. Quarterly of Applied Mathematics, 70, 133-157. https://doi.org/10.1090/S0033-569X-2011-01246-9
- 15. Kilbas, A.A., Srivastava, H.M. and Trujillo, J.J. (2006) Theory and Applications of Fractional Differential Equations, Vol 204. Elsevier Science B.V., Amsterdam. https://doi.org/10.1016/S0304-0208(06)80001-0








