Journal of Applied Mathematics and Physics
Vol.04 No.12(2016), Article ID:72551,9 pages
10.4236/jamp.2016.412210
The Advection Wave-in-Secondary Saturation Movement Equation and Its Application to Concentration Tension-Driven Saturation Kinetic Flow
Tafireyi Nemaura1,2
1Department of Clinical Pharmacology, University of Zimbabwe, Harare, Zimbabwe
2Department of Applied Mathematics, National University of Science and Technology, Bulawayo, Zimbabwe
Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: November 14, 2016; Accepted: December 3, 2016; Published: December 6, 2016
ABSTRACT
The deterministic description of a wave of solution particle of efavirenz is given. Simulated pharmacokinetic data points from patients on efavirenz are used. The one dimensional wave equation is used to infer on transfer of vibrations due to tension between solution particles. The work investigates movement using wave analogy, but in a different variable space. Two important movement fluxes of a wave are derived an attracting one identified as tension conductivity and a dispersing one identified as tension diffusivity. The Wave Equation can be used to describe another spin-off movement flux formed induced by vibrations in solution particle.
Keywords:
Partial Differential Equations, Wave, Movement Flux

1. Introduction
There is a rich history of quantum mechanics that investigates wave-particle duality using light [1] [2] . We derive a one dimensional wave equation in the context of particle movement [3] . This equation has extensively been studied beginning with work proposed by D’Alembert [4] . Furthermore, this work supports the hypothesis advanced by Louis de Broglie that all matter manifests a wave like nature. An idea further developed by David Bohm, who postulated that every material particle is accompanied by a field which guides the motion of the particle. This field evolves according to the Schrödinger’s equation [2] . In this work we retain the conventional wave equation. It models the advective entity of a wave and proposes an extension to other components of movement flux which are passive, convective and saturation.
This work derives characterisation of a wave and shows it as a spin-off movement flux that is derived from tension in the vibrations of the solution particle. It is described as a spin-off of a solution particle or the pilot wave [2] . Furthermore, this spin-off flux is deterministic. However, other researchers consider a probabilistic view of the quantum state [2] [5] . The secondary saturation movement in the concentration-time space is used to investigate the behaviour of the wave [6] . The mathematical formulation brings to light an understanding of the wave part of a solution particle. Waves in location and time space have been studied by other researchers [1] [7] . The wave is studied in a different space (concentration-time) and analogies are proposed. A relationship of a wave is derived, with the aid of simulated pharmacokinetic data in-vivo.
In addition, this work shows that a wave is a system with four primary movement components of flux. The total flux at any given concentration is zero. The system formed is similar to that obtained for the one that facilitates exchange of concentration through gradient [8] . The system evolves with time. There are two forms of flux the conductivity and diffusivity.
2. Methods
Simulated projected data on secondary saturation movement, time and concentration was obtained from pharmacokinetic projections made on patients on 600 mg dose of efavirenz considered in Nemaura (2015, 2016). Partial and Ordinary Differential equations are used in the development of models that characterizes wave motion. A statistical Package R, is used to develop nonlinear regression models.
Derivation of Advection Kinetic Flow for the Secondary Saturation Movement Due to Tension
Consider 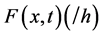 the secondary saturation movement at time t and concentration x-(tension-driven transportation inducing measure) in the blood. The variable
the secondary saturation movement at time t and concentration x-(tension-driven transportation inducing measure) in the blood. The variable  is also a measurement of tension density of movement. In addition, the variable
is also a measurement of tension density of movement. In addition, the variable 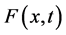 is taken to denote the (vertical) displacement at time t of the concentration
is taken to denote the (vertical) displacement at time t of the concentration 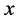 on the advection string component. The rate at which saturation movement crosses a solution particle is proportional to concentration, time and secondary saturation move- ment of solution particle [8] . The following proposition is made that the amount of
on the advection string component. The rate at which saturation movement crosses a solution particle is proportional to concentration, time and secondary saturation move- ment of solution particle [8] . The following proposition is made that the amount of
tension advective conductivity flux of solution particle 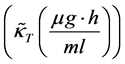 is the difference
is the difference
between 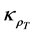 (that amount of tension advective conductivity flux which is generated by movement density
(that amount of tension advective conductivity flux which is generated by movement density 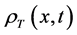 (obtaining in the process of solution formation)) and
(obtaining in the process of solution formation)) and 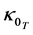 (an already existing constant (base) amount of tension advective conductivity flux (primarily obtaining in the independent of solute of x, solvent state)). The function of proportionality is called the amount of tension advective conductivity flux and is de- noted by
(an already existing constant (base) amount of tension advective conductivity flux (primarily obtaining in the independent of solute of x, solvent state)). The function of proportionality is called the amount of tension advective conductivity flux and is de- noted by 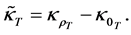 The functions
The functions 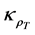 and
and 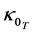 are such that
are such that 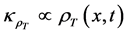 and
and 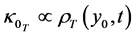 where
where 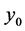 is the homogenous concentration mix in the base solvent without solute
is the homogenous concentration mix in the base solvent without solute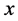 , thus
, thus 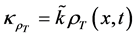
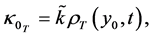 and where
and where 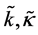 are constants of direct proportionality associated with the tension,
are constants of direct proportionality associated with the tension,

In a homogenous mix, 
[tension advective conductivity flux in the solvent of a solute of


Consider a small element of the string (bridge) between the two concentration points 




Let 







The total vertical tension advective flux acting on the element is

where 






and

From Equations (1)-(5) and the approximation formulas for 

The concentration-time amount of form movement due to tension in the solution
particle bridge is 
place 

where,
Thus,

At the limit

The following result is immediate,

where,
is the secondary saturation tension advective conductivity flux 

where,
The terms,
are secondary saturation tension base-advection diffusivity flux
turation tension advection diffusivity
rest tension advection conductivity flux 
The following relation from Equations (10) and (11) is established between tension advection conductivity and diffusivity fluxes,

where
It is important to note that 
3. Results
Applications to Deteministic Saturation Tension Advection Kinetic Flow of Concentration of Efavirenz and Numerical Analysis
We consider the secondary saturation 

where, 


Following from Equation (13), Equation (10) assume the form of,

and Equation (11) becomes,

The following conditions holds for secondary saturation tension advective diffusivity 
Table 1.Parameter estimates in modelling saturation movement rate with respect to t (Model 13(i)).
Table 2.Parameter estimates in modelling saturation movement rate with respect to x (Model 13(ii)).
It is noted that for 

The reference spin-off advective flux is investigated and the constituent behaviour is suggested by Equation (16) (Table 3),

Figure 1. Time matched plot of the spin-off advection diffusivity of saturation movement in relation to concentration.
Table 3. Parameter estimates in modelling saturation movement spin-off diffusivity fluxes in Equation (16).







The characterisation of the four main spin-off diffusivity flux entities are shown and magnitudes of effects (Figure 2).

where, 


4. Conclusions
A wave in this work has been shown to be a spin-off movement flux of a solution particle. It also has the same component characterisation as a solution particle at primary level. It consists of the advective, passive, saturation and convective components [6] [8] . A wave has generally slower movement flux components relative to gradient driven
Figure 2. Components of the spin-off diffusivity flux in time.
Figure 3. Summary scatter time-matched plot of the relationship between the following variables 

movement flux components [8] . There have been several experiments that support De Broglie’s assertions [2] . This work removes the notion of tracking the wave using location with the aid of a probability distribution derived from Schrödinger [5] . It proposes a different space related to kinetic solubility of a solution particle to track it’s wave [6] .
Considering a different unique space, we obtain similar characterisation of flux of a wave to that of gradient-driven diffusion. These two are system flux movements in time. A conclusion is reached that these two forms are characterised similar pattern of move- ment [8] . The heat (diffusion) and wave equations are two fundamental equations [3] [9] . They describe two forms of advective movements. The heat and wave equations are derived from gradient and tension forms of movement respectively.
Acknowledgements
The author would like to thank the following; C. Nhachi, C. Masimirembwa, and G. Kadzirange, AIBST and The College of Health Sciences, University of Zimbabwe.
Cite this paper
Nemaura, T. (2016) The Advection Wave-in-Secondary Saturation Movement Equation and Its Application to Concentration Tension-Driven Saturation Kinetic Flow. Journal of Applied Mathematics and Physics, 4, 2126-2134. http://dx.doi.org/10.4236/jamp.2016.412210
References
- 1. Tsaparlis, G. (2001) Towards a Meaningful Introduction to the Schrödinger Equation through Historical and Heuristic Approaches. Chemistry Education, Research and Practice, 2, 203-213.
https://doi.org/10.1039/B1RP90023D - 2. Jagielski, B. (2009) Elements of the Wave-Particle Duality of Light. Master Thesis, University of Oslo, Oslo.
- 3. Meziani, A. (2016) The Wave Equation.
http://www2.fiu.edu/meziani/NOTE2.pdf - 4. Cannon, J.T. and Dostrovsky, S. (1981) The Evolution of Dynamics: Vibration Theory from 1687 to 1742. Springer-Verlag, New York.
https://doi.org/10.1007/978-1-4613-9461-7 - 5. Halliday, D., Resnik, R. and Walker, J. (2001) Fundamentals of Physics. 6th Edition, John Wiley and Sons, New York.
- 6. Nemaura, T. (2015) Modeling Transportation of Efavirenz: Inference on Possibility of Mixed Modes of Transportation and Kinetic Solubility. Frontiers in Pharmacology, 6, 121.
https://doi.org/10.3389/fphar.2015.00121 - 7. Sengupta, D.L. and Sarkar, T.K. (2003). Maxwell, Hertz, the Maxwellians, and the Early History of Electromagnetic Waves. IEEE Antennas and Propagation Magazine, 45, 13-19.
https://doi.org/10.1109/MAP.2003.1203114 - 8. Nemaura, T. (2016) The Advection Diffusion-in-Secondary Saturation Movement Equation and Its Application to Concentration Gradient-Driven Saturation Kinetic Flow. Journal of Applied Mathematics and Physics, 4, 1998-2010.
- 9. Narasimhan, T.N. (1999) Fourier’s Heat Conduction Equation: History, Influence, and Connections. Reviews of Geophysics, 37, 151-172.
https://doi.org/10.1029/1998RG900006
















