Journal of Applied Mathematics and Physics
Vol.04 No.01(2016), Article ID:62663,5 pages
10.4236/jamp.2016.41008
The Scaling of Entanglement Entropy for One Spatial XXZ Spin Chain
Honglei Wang1, Chunhuan Xiang2*
1College of Medical Informatics, Chongqing Medical University, Chongqing, China
2School of Public Health and Management, Chongqing Medical University, Chongqing, China

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 6 December 2015; accepted 10 January 2016; published 13 January 2016
ABSTRACT
We investigate the scaling of entanglement entropy for one spatial XXZ spin chain by using matrix product states to approximate ground states. The entanglement entropy scales logarithmically with a coefficient that is determined by the associated conformal field theory, the quantum phase transitions occurred between Large-D and Halde phase, Halde phase and Neel phase. The scaling relation-ship is given in this paper.
Keywords:
Entanglement Entropy, Quantum Phase Transitions, Scaling, Numerical Simulation

1. Introduction
The study of quantum condensed matter systems is benefiting from an infusion of ideas related to quantum information and quantum entanglement. Quantum entanglement plays an important role in distinguishing the nature between the quantum systems and classical systems. It also connects quantum information theory to the traditional quantum many-body systems. More recently, entanglement has emerged on the nearby stage of quantum many-body physics, especially for systems that exhibit quantum phase transitions [1] -[6] , where it can play the role of a diagnostic of quantum correlations. Quantum phase transitions [7] are transitions between qualitatively distinct phases of quantum many-body systems, driven by quantum fluctuations. However, quantum many body systems are very hard to study due to the exponential growth of their Hilbert space with the number of constituents. By employing the matrix product states to approximate ground states [8] [9] , the entanglement entropy for one dimensional spin system is obtained. It is thus obvious that the matrix product states with matrices of finite size cannot describe exactly the behavior of an infinite system at the critical point but we may try to find the exact amount of entanglement which is captured.
The important information is embeded in the way a state approaches the thermodynamic limit and one can extract it by using the celebrated finite size scaling technique [10] . This technique amounts to study even larger systems in a gapless phase and extract universal properties through the dependence of the physical observables on the truncation dimension of the matrix.
The rest of this paper is organised as follows. In Section 2, we recall the physics of spin-1 models with long- range interactions. Section 3 discusses the entanglement entropy and the scaling relationship of the spin-1 model and shows our simulation results for the one-dimensional spin-1 model. Finally, Section 4 contains our conclusions.
2. The One Dimensional Spin-1 XXZ Model with Uniaxial Single-Ion-Type Anisotropy
One-dimensional antiferromagnetic spin chains have been the subject of recent investigations by numerous groups. The Hamiltonian for spin-1 XXZ model with uniaxial single-ion-type anisotropy [11] is given as
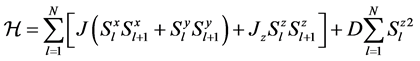
where J = 1 to fix the energy scale, 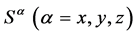 spin-1 operator, D represents uniaxial single-ion anisotropy, Jz is the controlable parameter. The ground-state phase diagram of the spin-1 model consists of the Haldane phase, the large-D phase, XY phases, the ferromagnetic phase, and the Neel phase [12] [13] . For the integer spin, there is a gap between the first excited state and the ground state.
spin-1 operator, D represents uniaxial single-ion anisotropy, Jz is the controlable parameter. The ground-state phase diagram of the spin-1 model consists of the Haldane phase, the large-D phase, XY phases, the ferromagnetic phase, and the Neel phase [12] [13] . For the integer spin, there is a gap between the first excited state and the ground state.
A gapful phase to gapful phase transition happened between the Haldane phase and large-D phase; the type of the quantum phase transition between the Neel phase and Haldane phase is the Ising transition. The central charge, which is associated with the universality class of the quantum phase transition, for the Ising transition is 0.5. Employing invariance under translations and parallelizability of local updates, matrix product states can simulate infinite systems directly, without resorting to costly, less accurate extrapolations. We obtain the approximate ground states of different truncation dimension for the spin-1 model by using matrix product states.
3. The Entanglement Entropy and Scaling Relationship for One Dimensional Spin-1 XXZ Model
The entanglement entropy is a measure of a bipartite entanglement present in a quantum state, whose behavior is, in many occasions, universal [14] . For a bipartite system AB that consists of the system A and the environment B. The reduced density matrix of the system A is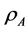 . The entanglement entropy
. The entanglement entropy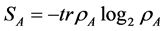 , which is used to measure the bipartite entanglement between A and B.
, which is used to measure the bipartite entanglement between A and B. 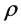 is become the
is become the 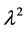 in the representation of ground state by the matrix product state,
in the representation of ground state by the matrix product state,  is a diagonal matrix. For all one-dimensional gapped quantum spin systems, the entanglement entropy saturates to a constant independently of the size of the block [15] . The entanglement obeys the scaling law
is a diagonal matrix. For all one-dimensional gapped quantum spin systems, the entanglement entropy saturates to a constant independently of the size of the block [15] . The entanglement obeys the scaling law 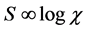 [16] [17] ,
[16] [17] , 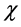 is the truncation dimension of the matrix product state. It is clear that the entanglement entropy of half of the infinite chain with the other half will diverge as
is the truncation dimension of the matrix product state. It is clear that the entanglement entropy of half of the infinite chain with the other half will diverge as 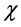 goes to infinity. The known results [16] - [18] shown that it can be used to characterize both quantum criticality and topological phases in a variety of quantum many-body systems.
goes to infinity. The known results [16] - [18] shown that it can be used to characterize both quantum criticality and topological phases in a variety of quantum many-body systems.
For the spin-1 model, the parameter Jz = 1, the quantum phase transitions between the Large-D phase and the Haldane phase are investigated by the entanglement entropy, which is shown in Figure 1. The critical points given by the truncation dimension are shown as: c = 20, 30, 40, 50, 60; D = 1.119, 1.073, 1.056, 1.039, 1.026, respectively. The entanglement entropy between the Haldane phase and the Neel phase is shown in Figure 2. The critical points given by the truncation dimension are shown as: c = 20, 30, 40, 50, 60; D = 0.810, 0.849, 0.876, 0.891, 0.900, respectively. The peak given by different truncation dimension is the pseudo-critical point, which is drawing near the critical point of the system.
The entanglement entropy scales logarithmically when the system becomes quantum-critical. The scaling relationship [19] -[22] between the entanglement and the correlation length is given as

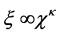 ,
, 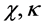 is the truncation dimension of the matrix product state and the free parameter, respectively. The scaling relationship is given as
is the truncation dimension of the matrix product state and the free parameter, respectively. The scaling relationship is given as
Figure 1. The entanglement entropy between the Large-D phase and the Haldane phase with Jz = 1. The critical points given by the truncation dimension are shown as: c = 20, 30, 40, 50, 60; D = 1.119, 1.073, 1.056, 1.039, 1.026, respectively.
Figure 2. The entanglement entropy between the Haldane phase and the Neel phase with Jz = 1. The critical points given by the truncation dimension are shown as: c = 20, 30, 40, 50, 60; D = 0.810, 0.849, 0.876, 0.891, 0.900, respectively.
The free parameters a and b can be obtained by fitting the entanglement entropy of the critical point given by the matrix product state and the corresponding truncation dimension. The fitting results for the quantum phase transitions between the Large-D phase and the Haldane phase and the quantum phase transition between the Haldane phase and the Neel phase are shown in Figure 3 and Figure 4. The scaling relationship between entanglement entropy S and truncation dimension c for the quantum phase transition between the Large-D phase and the Haldane phase is given with a = 0.226, b = 0.509. The scaling relationship between entanglement entropy S and truncation dimension c for the quantum phase transition between the Haldane phase and the Neel phase is given with a = 0.185, b = 0.753.
4. Conclusion
We investigate the scaling of entanglement entropy for one spatial XXZ spin chain by using matrix product states to approximate ground states. The entanglement entropy scales logarithmically with a coefficient that is determined by the associated conformal field theory, the quantum phase transitions occurred between Large-D
Figure 3. The scaling relationship between entanglement entropy S and truncation dimension c is shown with a = 0.226, b = 0.509.
Figure 4. The scaling relationship between entanglement entropy S and truncation dimension c is shown with a = 0.185, b = 0.753.
and Halde phase, Halde phase and Neel phase. We have shown that the entanglement entropy is an efficient quantity in characterizing the Ising transitions and the Gaussian transitions in one dimension. The scaling plays crucial roles on identifying a quantum system with a physically different classical system. We hope that our results will be useful in studying the quantum spin system in one dimension.
Acknowledgements
This work was financially supported by the National Natural Science Foundation of China (Grant No. 11447115) and the Science Foundation of Chongqing City Board of Education (KJ121206).
Cite this paper
HongleiWang,ChunhuanXiang, (2016) The Scaling of Entanglement Entropy for One Spatial XXZ Spin Chain. Journal of Applied Mathematics and Physics,04,48-52. doi: 10.4236/jamp.2016.41008
References
- 1. Osborne, T.J. and Nielsen, M.A. (2002) Entanglement in a Simple Quantum Phase Transition. Physical Review A, 66, 032110-4.
http://dx.doi.org/10.1103/PhysRevA.66.032110 - 2. Osterloh, A., Amico, L. Falei, G. and Fazio, R. (2002) Scaling of Entanglement Close to a Quantum Phase Transition. Nature (London), 416, 608-611.
http://dx.doi.org/10.1038/416608a - 3. Vidal, G., Latorre, J.I., Rico, E. and Kitaev, A. (2003) Entanglement in Quantum Critical Phenomena. Physical Review Letters, 90, 227902-4.
http://dx.doi.org/10.1103/PhysRevLett.90.227902 - 4. Barnum, H., Russek, S.E. and Silva, T.J. (2004) A Subsystem-Independent Generalization of Entanglement. Physical Review Letters, 92, 107902-4.
http://dx.doi.org/10.1103/PhysRevLett.92.107902 - 5. Lambert, N., Emary, C. and Brandes, T. (2004) Entanglement and the Phase Transition in Single-Mode Superradiance. Physical Review Letters, 92, 073602-4.
http://dx.doi.org/10.1103/PhysRevLett.92.073602 - 6. Gu, S.-J., Deng, S.-S., Li, Y.-Q. and Lin, H.-Q. (2004) Entanglement and Quantum Phase Transition in the Extended Hubbard Model. Physical Review Letters, 93, 086402-4.
http://dx.doi.org/10.1103/PhysRevLett.93.086402 - 7. Sachdev, S. (1999) Quantum Phase Transitions. Cambridge University Press, Cambridge.
- 8. Vidal, G. (2007) Classical Simulation of Infinite-Size Quantum Lattice Systems in One Spatial Dimension. Physical Review Letters, 98, 070201.
http://dx.doi.org/10.1103/PhysRevLett.98.070201 - 9. Vidal, G. (2004) Efficient Simulation of One-Dimensional Quantum Many-Body Systems. Physical Review Letters, 93, 040502.
http://dx.doi.org/10.1103/PhysRevLett.93.040502 - 10. Barber, M.N. (1983) Phase Transitions and Critical Phenomena Edited by Domb, C. and Lebowitz, J.L., Vol. 8. Academic, New York.
- 11. Chen, W., Hida, K. and Sanctuary, B.C. (2003) Ground-State Phase Diagram of S = 1 XXZ Chains with Uniaxial Single-Ion-Type Anisotropy. Physical Review B, 67, Article ID: 104401.
http://dx.doi.org/10.1103/PhysRevB.67.104401 - 12. Schulz, H.-J. (1986) Phase Diagrams and Correlation Exponents for Quantum Spin Chains of Arbitrary Spin Quantum Number. Physical Review B, 34, 6372.
http://dx.doi.org/10.1103/PhysRevB.67.104401 - 13. Nijs, M. and Rommelse, K. (1989) Preroughening Transitions in Crystal Surfaces and Valence-Bond Phases in Quantum Spin Chains. Physical Review B, 40, 4709-4734.
http://dx.doi.org/10.1103/PhysRevB.40.4709 - 14. Amico, L., Fazio, R., Osterloh, A. and Vedral, V. (2008) Entanglement in Many-Body Systems. Review Modern Physical, 80, 517-576.
http://dx.doi.org/10.1103/RevModPhys.80.517 - 15. Hastings, M.B. (2007) An Area Law for One-Dimensional Quantum Systems. Journal of Statistics and Mechanics, 2007, Article ID: P08024.
http://dx.doi.org/10.1088/1742-5468/2007/08/p08024 - 16. Wang, H.L. and Xiong, X.L. (2014) The Finite Scaling for S = 1 XXZ Chains with Uniaxial Single-Ion-Type Anisotropy. The European Physical Journal D, 68, 54.
http://dx.doi.org/10.1140/epjd/e2014-40426-y - 17. Calabrese, P. and Cardy, J. (2004) Entanglement Entropy and Quantum Field Theory. Journal of Statistics and Mechanics, 2004, Article ID: P06002.
http://dx.doi.org/10.1088/1742-5468/2004/06/p06002 - 18. Ryu, S. and Hatsugai, Y. (2006) Entanglement Entropy and the Berry Phase in the Solid State. Physical Review B, 73, Article ID: 245115.
http://dx.doi.org/10.1103/PhysRevB.73.245115 - 19. Lepori, L., De Chiara, G. and Sanpera, A. (2013) Scaling of the Entanglement Spectrum near Quantum Phase Transitions. Physical Review B, 87, Article ID: 235107.
http://dx.doi.org/10.1103/physrevb.87.235107 - 20. Nagy, A. (2011) Exploring Phase Transitions by Finite-Entanglement Scaling of MPS in the 1D ANNNI Model. New Journal of Physics, 13, Article ID: 023015.
http://dx.doi.org/10.1088/1367-2630/13/2/023015 - 21. Matsueda, H. (2011) Scaling of Entanglement Entropy and Hyperbolic Geometry. arXiv: 1112.5566.
- 22. Pirvu, B., Vidal, G., Verstraete, F. and Tagliacozzo, L. (2012) Matrix Product States for Critical Spin Chains: Finite Size Scaling versus Finite Entanglement Scaling. Physical Review B, 86, Article ID: 075117.
http://dx.doi.org/10.1103/physrevb.86.075117
NOTES
*Corresponding author.







