Journal of Applied Mathematics and Physics
Vol.03 No.12(2015), Article ID:61765,9 pages
10.4236/jamp.2015.312181
Analytical Treatment of the Evolutionary (1 + 1)-Dimensional Combined KdV-mKdV Equation via the Novel (G'/G)-Expansion Method
Md. Nur Alam1*, Fethi Bin Muhammad Belgacem2, M. Ali Akbar3
1Department of Mathematics, Pabna University of Science & Technology, Pabna, Bangladesh
2Department of Mathematics, Faculty of Basic Education, PAAET, Al-Ardhiya, Kuwait
3Department of Applied Mathematics, University of Rajshahi, Rajshahi, Bangladesh

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 24 October 2015; accepted 5 December 2015; published 8 December 2015

ABSTRACT
The novel (G'/G)-expansion method is a powerful and simple technique for finding exact traveling wave solutions to nonlinear evolution equations (NLEEs). In this article, we study explicit exact traveling wave solutions for the (1 + 1)-dimensional combined KdV-mKdV equation by using the novel (G'/G)-expansion method. Consequently, various traveling wave solutions patterns including solitary wave solutions, periodic solutions, and kinks are detected and exhibited.
Keywords:
Novel (G'/G)-Expansion Method, (1 + 1)-Dimensional Combined KdV-mKdV Equation, Kink Patterns, Nonlinear Evolution Equation, Solitary Wave Solutions, Traveling Wave Solutions

1. Introduction
NLEEs arise in a wide variety of disciplines physical problems such as in physics, biology, fluid mechanics, solid-state physics, biophysics, solid mechanics, condensed matter physics, plasma physics, quantum mechanics, optical fibers, elastic media, reaction-diffusion models, and quantum field theory. Recently, many kinds of powerful methods have been proposed to find exact traveling wave solutions of NLEEs e.g., the 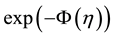 - expansion [1] -[3] , the (G'/G)-expansion method [4] -[7] , the wave translation method [8] , the Ansatz method [9] [10] , the Darboux transformation method [11] , the Hopf-Coletrans formation [12] , the Miura transformation [13] , the Jacobi elliptic function method [14] , the A domian decomposition method [15] [16] , the method of bifurcation of planar dynamical systems [17] [18] , the inverse scattering transform method [19] , the multiple- expansion method [20] , Homotopy analysis method [21] [22] , three-wave method [23] , extended homoclinic test approach [24] , the improved F-expansion method [25] , the projective Riccati equation method [26] , and the Weirstrass elliptic function method [27] to name a few. The novel (G'/G)-expansion method is beginning to find a pragmatic ever increasing use as can be seen in [28] -[33] . Worthy is it to note perhaps that rudiments of the (G'/G)-expansion method was used by Eckstein and Belgacem, as early as the late 80’s, to describe the platelet transport behavior in blood vessels, [34] -[36] . Recently, Alam and Belgacem in their study appearing in the Waves, Wavelets and Fractals-Abstract Analysis Journal, applied the novel method to the long wave equation, [37] . The aim of this paper is to find exact and solitary wave solutions of the (1 + 1)-dimensional combined KdV-mKdV equation by the novel (G'/G)-expansion method.
- expansion [1] -[3] , the (G'/G)-expansion method [4] -[7] , the wave translation method [8] , the Ansatz method [9] [10] , the Darboux transformation method [11] , the Hopf-Coletrans formation [12] , the Miura transformation [13] , the Jacobi elliptic function method [14] , the A domian decomposition method [15] [16] , the method of bifurcation of planar dynamical systems [17] [18] , the inverse scattering transform method [19] , the multiple- expansion method [20] , Homotopy analysis method [21] [22] , three-wave method [23] , extended homoclinic test approach [24] , the improved F-expansion method [25] , the projective Riccati equation method [26] , and the Weirstrass elliptic function method [27] to name a few. The novel (G'/G)-expansion method is beginning to find a pragmatic ever increasing use as can be seen in [28] -[33] . Worthy is it to note perhaps that rudiments of the (G'/G)-expansion method was used by Eckstein and Belgacem, as early as the late 80’s, to describe the platelet transport behavior in blood vessels, [34] -[36] . Recently, Alam and Belgacem in their study appearing in the Waves, Wavelets and Fractals-Abstract Analysis Journal, applied the novel method to the long wave equation, [37] . The aim of this paper is to find exact and solitary wave solutions of the (1 + 1)-dimensional combined KdV-mKdV equation by the novel (G'/G)-expansion method.
2. Description of the Method
For a given nonlinear wave equation with one physical field 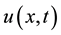 in two variables x and t
in two variables x and t
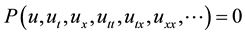 (1)
(1)
where 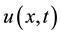 and P is a polynomial about u in and its derivatives.
and P is a polynomial about u in and its derivatives.
Let us consider that the traveling wave variable is
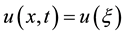 ,. (2)
,. (2)
The traveling wave variable (2), transforms (1) into a nonlinear ODE for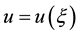 :
:
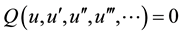 . (3)
. (3)
We seek for the solution of Equation (3) in the following generalized ansatze
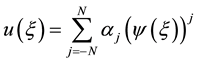 , (4)
, (4)
where
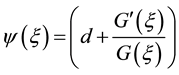 . (5)
. (5)
Herein 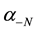 or αN might be zero, but both of them could not be zero simultaneously. αj
or αN might be zero, but both of them could not be zero simultaneously. αj 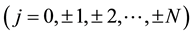 and d are constants to be determined later and
and d are constants to be determined later and 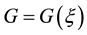 satisfies the second order nonlinear ODE:
satisfies the second order nonlinear ODE:
 (6)
(6)
where prime denotes the derivative with respect to  and
and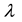 ,
, 

The Cole-Hopf transformation 

Equation (7) has individual twenty five solutions (see Zhu, [38] for details).
The value of the positive integer N can be determined by balancing the highest order linear terms with the nonlinear terms of the highest order come out in Equation (3). If the degree of 


Substituting Equation (4) including Equations (5) and (6) into Equation (3), we obtain polynomials in



sulted polynomials to zero, yields an over-determined set of algebraic equations for
Suppose the value of the constants can be obtained by solving the algebraic equations obtained in Step 4. Substituting the values of the constants together with the solutions of Equation (6), we will obtain some new and comprehensive exact traveling wave solutions to the nonlinear evolution Equation (1).
3. The (1 + 1)-Dimensional Combined KdV-mKdV Equation
In this section, we will employ the novel (G'/G)-expansion method to get several novel and further wide-ranging exact traveling wave solutions to the famous (1 + 1)-dimensional combined KdV-mKdV equation.
Let us consider the (1 + 1)-dimensional combined KdV-mKdV equation

Using the traveling wave transformation

Integrating Equation (9), we obtain

where C is a constant of integration. Inserting Equation (4) into Equation (10) and balancing the highest order derivative 


Therefore, the solution of Equation (10) takes the form,

Substituting Equation (11) into Equation (10), the left hand side is transformed into polynomials of



nomials to zero, we obtain an over-determine set of algebraic equations (for simplicity we leave out to display the equations) for



where d, 


For Set, substituting Equation (12) and the values of 
When 



where









where A and B are real constants.




When 









where A and B are arbitrary constants such that




When 



where k is an arbitrary constant.
When 


where 
4. Conclusion
In this letter, the novel (G'/G)-expansion method has been successfully applied to find the exact solution for the (1 + 1)-dimensional combined KdV-mKdV equation. The novel (G'/G)-expansion method is used to find a new exact traveling wave solution. The results show that the novel (G'/G)-expansion method is reliable and effective tool to solve the (1 + 1)-dimensional combined KdV-mKdV equation. Thus the novel (G'/G)-expansion method could be a powerful mathematical tool for solving NLEEs.
Acknowledgements
The Authors offer sincere thanks to the referees and editorial board of JAMP for their helpful and kind support. Furthermore, Fethi Bin Muhammad Belgacem is pleased to acknowledge the continued support of the Public Authority for Applied Education and Training (PAAET RD) for their continued support.
Cite this paper
Md. NurAlam,Fethi Bin MuhammadBelgacem,M. AliAkbar, (2015) Analytical Treatment of the Evolutionary (1 + 1)-Dimensional Combined KdV-mKdV Equation via the Novel (G'/G)-Expansion Method. Journal of Applied Mathematics and Physics,03,1571-1579. doi: 10.4236/jamp.2015.312181
References
- 1. Hafez, M.G., Alam, Md.N. and Akbar, M.A. (2015) Traveling Wave Solutions for Some Important Coupled Nonlinear Physical Models via the Coupled Higgs Equation and the Maccari System. Journal of King Saud University—Science, 27, 105-112.
http://dx.doi.org/10.1016/j.jksus.2014.09.001 - 2. Alam, Md.N., Hafez, M.G., Akbar, M.A. and Roshid, H.O. (2015) Exact Traveling Wave Solutions to the (3 + 1)-Dimensional mKdV-ZK and the (2 + 1)-Dimensional Burgers Equations via Exp(-Eta)-Expansion Method. Alexandria Engineering Journal, 54, 635-644.
http://dx.doi.org/10.1016/j.aej.2015.05.005 - 3. Roshid, H.O., Alam, Md.N. and Akbar, M.A. (2015) Traveling Wave Solutions for Fifth Order (1 + 1)-Dimensional Kaup-Keperschmidt Equation with the Help of Exp(-Phi)-Expansion Method. Walailak Journal of Science and Technology, 12, 1063-1073.
- 4. Wang, M., Li, X. and Zhang, J. (2008) The (G'/G)-Expansion Method and Traveling Wave Solutions of Nonlinear Evolution Equations in Mathematical Physics. Physics Letters A, 372, 417-423.
http://dx.doi.org/10.1016/j.physleta.2007.07.051 - 5. Alam, Md.N., Akbar, M.A. and Hoque, M.F. (2014) Exact Traveling Wave Solutions of the (3 + 1)-Dimensional mKdV-ZK Equation and the (1 + 1)-Dimensional Compound KdVB Equation Using New Approach of the Generalized (G'/G)-Expansion Method. Pramana Journal of Physics, 83, 317-329.
http://dx.doi.org/10.1007/s12043-014-0776-8 - 6. Alam, Md.N. and Akbar, M.A. (2015) Some New Exact Traveling Wave Solutions to the Simplified MCH Equation and the (1 + 1)-Dimensional Combined KdV-mKdV Equations. Journal of the Association of Arab Universities for Basic and Applied Sciences, 17, 6-13.
http://dx.doi.org/10.1016/j.jaubas.2013.12.001 - 7. Alam, Md.N. and Akbar, M.A. (2014) Traveling Wave Solutions for the mKdV Equation and the Gardner Equation by New Approach of the Generalized (G'/G)-Expansion Method. Journal of the Egyptian Mathematical Society, 22, 402-406.
http://dx.doi.org/10.1016/j.joems.2014.01.001 - 8. Russell, J.S. (1844) Report on Waves. Proceedings of the 14th Meeting of the British Association for the Advancement of Science.
- 9. Hu, J.L. (2001) Explicit Solutions to Three Nonlinear Physical Models. Physics Letters A, 287, 81-89.
http://dx.doi.org/10.1016/S0375-9601(01)00461-3 - 10. Hu, J.L. (2001) A New Method for Finding Exact Traveling Wave Solutions to Nonlinear Partial Differential Equations. Physics Letters A, 286, 175-179.
http://dx.doi.org/10.1016/S0375-9601(01)00291-2 - 11. Matveev, V.B. and Salle, M.A. (1991) Darboux Transformation and Solitons. Springer, Berlin.
http://dx.doi.org/10.1007/978-3-662-00922-2 - 12. Salas, A.H. and Gomez, C.A. (2010) Application of the Cole-Hopf Transformation for Finding Exact Solutions to Several Forms of the Seventh-Order KdV Equation. Mathematical Problems in Engineering, 2010, Article ID: 194329.
http://dx.doi.org/10.1155/2010/194329 - 13. Bock, T.L. and Kruskal, M.D. (1979) A Two-Parameter Miura Transformation of the Benjamin-Ono Equation. Physics Letters A, 74, 173-176.
http://dx.doi.org/10.1016/0375-9601(79)90762-X - 14. Chen, Y. and Wang, Q. (2005) Extended Jacobi Elliptic Function Rational Expansion Method and Abundant Families of Jacobi Elliptic Functions Solutions to (1 + 1)-Dimensional Dispersive Long Wave Equation. Chaos, Solitons & Fractals, 24, 745-757.
http://dx.doi.org/10.1016/j.chaos.2004.09.014 - 15. Adomian, G. (1994) Solving Frontier Problems of Physics: The Decomposition Method. Kluwer Academic Publishers, Boston.
http://dx.doi.org/10.1007/978-94-015-8289-6 - 16. Wazwaz, A.M. (2002) Partial Differential Equations: Method and Applications. Taylor and Francis, London.
- 17. Li, J.B. and Liu, Z.R. (2000) Smooth and Non-Smooth Traveling Waves in a Nonlinearly Dispersive Equation. Applied Mathematical Modelling, 25, 41-56.
http://dx.doi.org/10.1016/S0307-904X(00)00031-7 - 18. Liu, Z.R. and Qian, T.F. (2001) Peakons and Their Bifurcation in a Generalized Camassa-Holm Equation. International Journal of Bifurcation and Chaos, 11, 781-792.
http://dx.doi.org/10.1142/S0218127401002420 - 19. Ablowitz, M.J. and Clarkson, P.A. (1991) Soliton, Nonlinear Evolution Equations and Inverse Scattering Method. Cambridge University Press, New York.
http://dx.doi.org/10.1017/CBO9780511623998 - 20. Malik, A., Chand, F., Kumar, H. and Mishra, S.C. (2012) Exact Solutions of the Bogoyavlenskii Equation Using the Multiple-Expansion Method. Computers & Mathematics with Applications, 64, 2850-2859.
http://dx.doi.org/10.1016/j.camwa.2012.04.018 - 21. Liao, S.J. (2005) A New Branch of Solutions of Boundary-Layer Flows over an Impermeable Stretched Plate. International Journal of Heat and Mass Transfer, 48, 2529-2539.
http://dx.doi.org/10.1016/j.ijheatmasstransfer.2005.01.005 - 22. Liao, S.J. (2009) A General Approach to Get Series Solution of Non-Similarity Boundary-Layer Flows. Communications in Nonlinear Science and Numerical Simulation, 14, 2144-2159.
http://dx.doi.org/10.1016/j.cnsns.2008.06.013 - 23. Darvishi, M.T. and Najafi, M. (2012) Some Exact Solutions of the (2 + 1)-Dimensional Breaking Soliton Equation Using the Three-Wave Method. World Academy of Science, Engineering and Technology, 87, 31-34.
- 24. Darvishi, M.T. and Najafi, M. (2012) Some Complexiton Type Solutions of the (3 + 1)-Dimensional Jimbo-Miwa Equation. World Academy of Science, Engineering and Technology, 87, 42-44.
- 25. Wang, D. and Zhang, H.Q. (2005) Further Improved F-Expansion Method and New Exact Solutions of Konopelchenko-Dubrovsky Equation. Chaos, Solitons & Fractals, 25, 601-610.
http://dx.doi.org/10.1016/j.chaos.2004.11.026 - 26. Yan, Z. (2003) Generalized Method and Its Application in the Higher-Order Nonlinear Schrodinger Equation in Nonlinear Optical Fibres. Chaos, Solitons & Fractals, 16,759-766.
http://dx.doi.org/10.1016/S0960-0779(02)00435-6 - 27. Kudryashov, N.A. (1990) Exact Solutions of the Generalized Kuramoto-Sivashinsky Equation. Physics Letters A, 147, 287-291.
http://dx.doi.org/10.1016/0375-9601(90)90449-X - 28. Alam, Md.N., Akbar, M.A. and Mohyud-Din, S.T. (2014) A Novel (G'/G)-Expansion Method and Its Application to the Boussinesq Equation. Chinese Physics B, 23, Article ID: 020203.
http://dx.doi.org/10.1088/1674-1056/23/2/020203 - 29. Alam, Md.N. and Akbar, M.A. (2014) Traveling Wave Solutions of the Nonlinear (1 + 1)-Dimensional Modified Benjamin-Bona-Mahony Equation by Using Novel (G'/G)-Expansion Method. Physical Review & Research International, 4, 147-165.
- 30. Alam, Md.N. (2015) Exact Solutions to the Foam Drainage Equation by Using the New Generalized (G'/G)-Expansion Method. Results in Physics, 5, 168-177.
http://dx.doi.org/10.1016/j.rinp.2015.07.001 - 31. Alam, Md.N., Hafez, M.G., Belgacem, F.B.M. and Akbar, M.A. (2015) Applications of the Novel (G'/G)-Expansion Method to Find New Exact Traveling Wave Solutions of the Nonlinear Coupled Higgs Field Equation. Nonlinear Studies, 22, 613-633.
- 32. Hafez, M.G., Alam, Md.N. and Akbar, M.A. (2014) Exact Traveling Wave Solutions to the Klein-Gordon Equation Using the Novel (G'/G)-Expansion Method. Results in Physics, 4, 177-184.
http://dx.doi.org/10.1016/j.rinp.2014.09.001 - 33. Alam, Md.N. and Akbar, M.A. (2015) A Novel (G'/G)-Expansion Method for Solving the (3 + 1)-Dimensional Modified KdV-Zakharov-Kuznetsov Equation in Mathematical Physics. International Journal of Computing Science and Mathematics, 6, 404-415.
- 34. Belgacem, F.B.M. and Smaoui, N. (2001) Interactions of Parabolic Convective Diffusion Equations and Navier-Stokes Equations Connected with Population Dispersal. Comm. Applied Nonlinear Anal, 8, 47-67.
- 35. Smaoui, N. and Belgacem, F.B.M. (2002) Connections between the Convective Diffusion Equation and the Forced Burgers Equation. Journal of Applied Mathematics and Stochastic Analysis, 15, 57-75.
http://dx.doi.org/10.1155/S1048953302000060 - 36. Eckstein, E. and Belgacem, F.B.M. (1991) Model of Platelet Transport in Flowing Blood with Drift and Diffusion Terms. Biophysical Journal, 60, 53-69.
http://dx.doi.org/10.1016/S0006-3495(91)82030-6 - 37. Alam, Md.N. and Belgacem, F.B.M. (2015) Application of the Novel (G'/G)-Expansion Method to the Regularized Long Wave Equation. Waves, Wavelets and Fractals—Advanced Analysis, 1, 20-36.
- 38. Zhu, S. (2008) The Generalized Riccati Equation Mapping Method in Non-Linear Evolution Equation: Application to (2 + 1)-Dimensional Boiti-Leon-Pempinelle Equation. Chaos, Solitons & Fractals, 37, 1335-1342.
http://dx.doi.org/10.1016/j.chaos.2006.10.015
NOTES
*Corresponding author.


