Received 5 June 2015; accepted 4 September 2015; published 7 September 2015

ABSTRACT

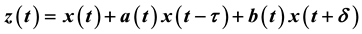In this paper, we obtained some sufficient conditions for the oscillation of all solutions of the second order neutral differential equation of the form where, and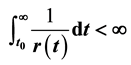. Examples are provided to ill- ustrate the main results.

Keywords:

Second Order, Nonlinear Differential Equation, Mixed Neutral Term, Oscillation

1. Introduction

In this paper, we are concerned with the oscillatory behavior of solutions of the second order nonlinear neutral differential equation of the form

(1)

where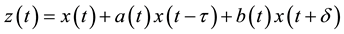, subject to the following conditions:

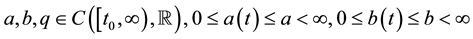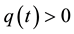(C₁), and for all;

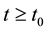(C₂)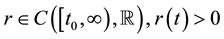, and;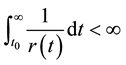

(C₃) 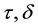are nonnegative constants, , , 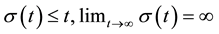and 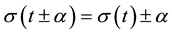for any;

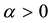(C₄) for, k is a constant.

By a solution of Equation (1), we mean a continuous function x defined on an interval such that is continuously differentiable and x satisfies Equation (1) for all. We consider only solu-

tions satisfying condition, and tacitly assume that Equation (1) possess such solu-

tions. As usual, a solution of Equation (1) is called oscillatory if it is neither eventually positive nor eventually negative; otherwise we call it nonosicllatory.

From the literature, it is known that second order neutral functional differential equations have applications in problems dealing with vibrating masses attached to an elastic bar and in some variational problems. For further applications and questions regarding existence and uniqueness of solutions of neutral functional differential equations, see [1] -[3] .

In recent years, there has been an increasing interest in establishing conditions for the oscillation or nonoscilla- tion of solution of neutral functional differential equations, see [4] -[20] for example, and the references cited therein.

In [21] , Xu and Meng obtained some sufficient conditions which guarantees that every solution x of equation (1) when, oscillates or.

Ye and Xu [22] studied equation when, and established some new oscillation criteria for Equation (1).

In [23] , Han et al. considered Equation (1) with and, and obtained some sufficient conditions which ensure that every solution of Equation (1) is oscillatory.

In [24] , the present authors established some sufficient conditions for the oscillation of all solutions of

Equation (1) when. Therefore in this paper we try to obtain some new oscillation criteria for

Equation (1). In Section 2, we use Riccati transformation technique to obtain some sufficient conditions for the oscillation of all solutions of Equation (1). Examples are provided in Section 3 to illustrate the main results.

2. Oscillation Results

In this section, we obtain some new oscillation criteria for the Equation (1). We begin with the following theorem.

Theorem 2.1 If

(2)

and

(3)

where, , and then every solution of Equation (1)

is oscillatory.

Proof. Suppose that is a nonsocillatory solution of Equation (1). Without loss of generality, we may assume that there exists such that. and for all. From the definition of, we have, and from Equation (1), is nonincreasing eventually. Hence, it is easy to conclude that there exist two possible cases of the sign of, that is, or for all.

First assume that for all. From the Equation (1), we have

or

(4)

Integrating (4) from to and using the fact for, we obtain

a contradiction to (2.1).

If, then we define the function by

(5)

Clearly. Nothing that is nonincreasing, we obtain

Dividing the last inequality by and integrating it from to, we obtain

Letting in the last inequality, we see that

Therefore,

(6)

From (5), we have

(7)

Next, we introduce another function by

(8)

Clearly. Noting that is nonincreasing, we have. Then,. From (6), we obtain

(9)

Similarly, we introduce another function by

(10)

Clearly. Since is nonincreasing, we have

Dividing the last inequality by and integrating it from to, we obtain

Letting, we see that

(11)

Differentiating (5), we obtain

(12)

Differentiating (8), we have

(13)

Differentiating (10), we have

(14)

Inview of (12), (13) and (14), we can obtain

(15)

From (4) and (15), we obtain

(16)

Multiplying (16) by and integrating from to, we have

From the above inequality, we obtain

Thus, it follows that

By (7), (9) and (11), we obtain that

which contradicts (3). The proof is now complete.

Corollary 2.1. Assume that with for. Further assume that (2.1) and (3) hold. Then every solution of Equation (1) is oscillatory.

Proof. The proof follows from Theorem 2.1.

Theorem 2.2. Assume that for. If condition (2.1) holds and

(17)

then every solution of Equation (1) is oscillatory.

Proof. Let be a nonsocillatory solution of Equation (1). Without loss of generality, we may assume that there exists such that and for all. By equation (1), is nonincreasing eventually. Hence, it is easy to conclude that there exist two possible cases of the sign of, that is, or for all. If, then we are back to the case of Theorem 2.1, and we can obtain a contradiction to (2.1). If, then we define and as in Theorem 2.1. Then proceed as in the proof of Theorem 2.1, we obtain (7), (9), (11) and (16) for. Multiplying (16) by and integrating from to yields

(18)

It follows from (C₂) and (7) that

Inview of (9), we have

From (11), we obtain

Therefore from (18), we obtain

which is a contradiction with (17). The proof is now complete.

Corollary 2.2. Assume that for. In condition (2.1) and (17) hold, then every solution of Equation (1) is oscillatory.

Proof. The proof follows from Theorem 2.2.

To prove our next theorem, we need a class of function and the operator T defined as follows:

Following [16] , we say that a function belongs to the function class, denoted by if, where, which satisfies and

for, and has the partial derivative on such that is locally integrable with

respect to in.

Define the operator by

(19)

for and. The function is defined by

(20)

then, it is easy to see that is a linear operator and

(21)

Theorem 2.3. Assume that, and there exist functions and such that

(22)

and

(23)

where is defined as in Theorem 2.1, the operator defined by (19), and is defined by (20). Then every solution of Equation (1) is oscillatory.

Proof. Let be a nonoscillatory solution of Equation (1). Then there exists a such that for all. Without loss of generality, we may assume that and for all. Then proceeding as in the proof of Theorem 2.1 we have

or and for all.

First assume that and for all. Define

(24)

Then, and

(25)

Since is nonincreasing and is increasing. Next, define

(26)

Then, and

(27)

Since is nonincreasing, is increasing and. Again, define

(28)

Then, and

(29)

Since is nonincreasing, is increasing and. Combining (25) and (29), and then using (4), we obtain

(30)

Now applying the operator to (30) and then using (21), we have

From the last inequality, we obtain

or

Taking the sup limit in the last inequality, we obtain a contradiction with (22).

Next consider the case and for all. From the proof of Theorem 2.1, we have the inequality (16). Now apply the operator to (16) and then using (21), we have

From the last inequality, we obtain

or

Taking the sup limit in the last inequality, we obtain a contradiction with (23). The proof is now completed.

Remark 2.1. With different choices of functions and, Theorem 2.3 can be stated with different con- ditions for oscillations of Equation (1).

For example, if we take for, then

From Theorem 2.3, we obtain the following oscillation criteria for Equation (1).

Corollary 2.3. Assume that, and there exists a function such that

and

where and. Then every solution of Equation (1) is oscillatory.

3. Examples

In this section, we provide three examples to illustrate the main results.

Example 3.1. Consider the neutral differential equation

(31)

Here, and. By taking and, it

is easy to see that all conditions of Theorem 2.1 are satisfied and hence every solution of Equation (31) is oscillatory.

Example 3.2. Consider the neutral differential equation

(32)

Here, and. By taking and

, it is easy to see that all conditions of Corollary 2.3 are satisfied and hence every solution of Equation (32) is oscillatory.

We conclude this paper with the following remark.

Remark 3.1. The results presented in [24] are not applicable to Equations (31) and (32) since in these

equations and the neutral term contains advanced arguments. Therefore, our results com-

plement and generalize some of the known results in the literature.

Cite this paper

RamalingamArul,Venkatachalam SubramaniyamShobha, (2015) Oscillation of Second Order Nonlinear Neutral Differential Equations with Mixed Neutral Term. Journal of Applied Mathematics and Physics,03,1080-1089. doi: 10.4236/jamp.2015.39134

References

NOTES

^*Corresponding author.