Journal of Applied Mathematics and Physics
Vol.03 No.07(2015), Article ID:57960,11 pages
10.4236/jamp.2015.37107
New Algorithms for Solving Bordered k-Tridiagonal Linear Systems
Moawwad El-Mikkawy*, Faiz Atlan
Mathematics Department, Faculty of Science, Mansoura University, Mansoura, Egypt
Email: *m_elmikkawy@yahoo.com, faizatlan11@yahoo.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 24 May 2015; accepted 12 July 2015; published 15 July 2015
ABSTRACT
The present article is mainly devoted for solving bordered k-tridiagonal linear systems of equations. Two efficient and reliable symbolic algorithms for solving such systems are constructed. The computational cost of the algorithms is obtained. Some illustrative examples are given.
Keywords:
Bordered k-Tridiagonal Matrices, Partitioned Matrices, Algorithm, LU Factorization, MAPLE

1. Introduction
In many scientific and engineering applications, different special linear systems of equations arise. For such systems the coefficient matrix has special structure. Sparse matrices which contain a majority of zeros occur are often encountered. It is usually more efficient to solve these systems using tailor-made algorithms, much faster and with less storage than a full matrix. This can be achieved by taking advantage of the special structure of the coefficient matrix. Important examples are tridiagonal matrices. Tridiagonal systems of linear equations take the form:
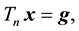 (1)
(1)
where
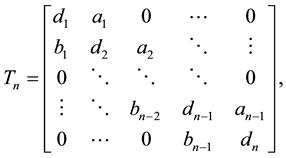 (2)
(2)
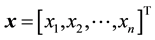 and
and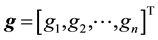 . The superscript T corresponds to the transpose operation. This type of matrices frequently appears in many applications, for example in parallel computing, telecommunication system analysis, solving differential equations using finite differences, heat conduction and fluid flow problems. A general
. The superscript T corresponds to the transpose operation. This type of matrices frequently appears in many applications, for example in parallel computing, telecommunication system analysis, solving differential equations using finite differences, heat conduction and fluid flow problems. A general
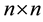 tridiagonal matrix of the form (2) can be stored in
tridiagonal matrix of the form (2) can be stored in
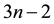 memory locations, rather than
memory locations, rather than
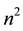 memory locations for a full matrix, by using three vectors
memory locations for a full matrix, by using three vectors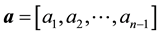 ,
,
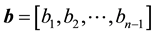 , and
, and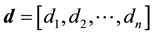 . This is always a good habit in computation in order to save memory space. To study tridiagonal matrices it is convenient to introduce a vector e defined by [1] [2] :
. This is always a good habit in computation in order to save memory space. To study tridiagonal matrices it is convenient to introduce a vector e defined by [1] [2] :
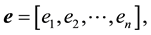 (3)
(3)
where
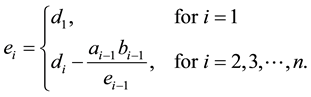 (4)
(4)
For some important results concerning tridiagonal matrix the reader may refer to [2] -[18] . The motivation of the current paper is to derive algorithms for solving bordered k-tridiagonal linear systems of the form:
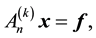 (5)
(5)
with
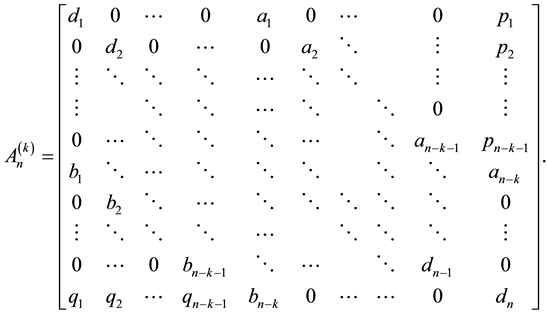 (6)
(6)
where ,
,
 and
and
The linear systems (5) for
Throughout this paper,

The organization of the paper is as follows: The main results are given in Section 2 and Section 3. Some illustrative examples are given in Section 4. A conclusion is given in Section 5.
2. Solving the System (5) via k-Tridiagonal Solvers
In this section, we are going to formulate a new symbolic algorithm, based on the Sherman-Morrison-Woodbury formula [29] , for solving bordered k-tridiagonal linear system of the form (5). By doing this, the solution of the system (5) reduces to solving three k-tridiagonal linear systems by using k-tridiagonal solvers such as these presented in [12] [30] .
Let us first note that the coefficient matrix,


where


and

By applying the Sherman-Morrison-Woodbury formula to


and

provided that the matrix

By making use of (7)-(12), we see that the solution of the bordered k-tridiagonal system (5) reduces to solving three k-tridiagonal linear systems by using k-tridiagonal solvers. Consequently, we may formulate the following symbolic algorithm for solving the linear system (5).
Algorithm 2.1. An algorithm for solving bordered k-tridiagonal linear systems.
To solve bordered k-tridiagonal linear systems of the form (5), we may proceed as follows:
INPUT: The entries of the matrix

OUTPUT: The solution vector
Step 1: Use the k-DETGTRI algorithm [12] to check the non-singularity of the matrix

Step 2: If

Step 3: Solve the three linear systems of k-tridiagonal type:



by using, for example, the k-Thomas solver in [12] then construct
Step 4: Compute the


If

Step 5: Compute

The computational cost of the algorithm is
It should be noted that the algorithm presented in [28] is a special case of the DB-kTRI1 algorithm when
3. Solving the System (5) Using the LU Factorization and Partition
In this section, we are going to consider the construction of a new algorithm for solving linear systems of equations of bordered k-tridiagonal type (5) by using partition. For this purpose it is convenient to introduce a vector



where


Consider the Doolittle LU factorization [31] of the coefficient matrix


where





Equation (14) can be rewritten in the form:

where
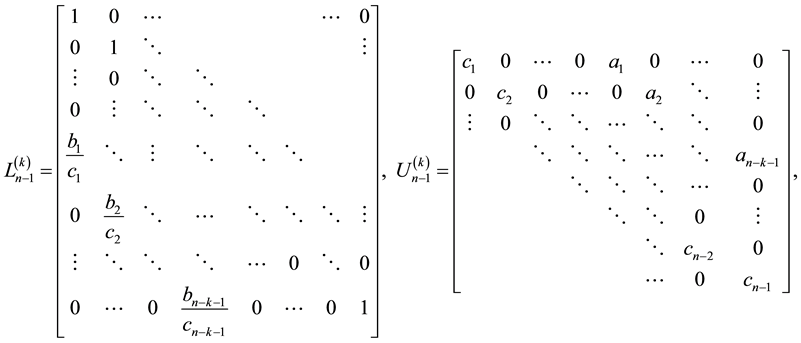



From (15), we see that the following four matrix equations must be satisfied.



and

Two cases will be considered:
CASE(I):
In this case, solving (18) and (19) for h and v respectively, yields:


CASE(II):
In this case, solving (18) and (19) for h and v respectively, gives:


In both cases, we have from (20),

At this stage, the determinant of the coefficient matrix in (6) can be computed using the following computational symbolic algorithm.
Algorithm 3.1. An algorithm for computing the determinant of bordered k-tridiagonal matrices.
To compute the determinant of a bordered k-tridiagonal matrix in (6), we may proceed as follows:
INPUT: Order of the matrix n, the value of k and the components,
OUTPUT: The determinant of the matrix

Step 1: Compute

If




Step 2: Compute

Step 3: Simplify


The Algorithm 3.1, will be referred to as DB-kDETGTRI algorithm.
Remarks:
1) The DETGTRI algorithm in [1] is a special case of DB-kDETGTRI algorithm when


2) The k-DETGTRI algorithm in [12] is a special case of DB-kDETGTRI algorithm when



3) The PERTRI algorithm in [8] is a special case of DB-kDETGTRI algorithm when




4) The DETSGCM algorithm in [32] is a special case of DB-kDETGTRI algorithm when











Now the linear system in (5), can be rewritten in partitioned form as:

where



To solve the linear system (26) it is equivalent to solve the two standard linear systems:

and

where


In conclusion, we may now formulate a second symbolic algorithm for solving the bordered k-tridiagonal linear system (5) as follows:
Algorithm 3.2. A symbolic algorithm for solving bordered k-tridiagonal linear systems using partition.
To solve a general bordered k-tridiagonal linear system of the form (5), we may proceed as follows:
INPUT: Order of the matrix n, the value of k and the components,


OUTPUT: The determinant of the matrix


Step 1: If

For

Set






End do
For

Compute and simplify:



End do.
For

Compute and simplify:



End do.
For

Compute and simplify:
End do.
Else
For

Set


End do
For

Compute and simplify:



End do.
For

Compute and simplify:
End do.
For

Compute and simplify:
End do.
For

Compute and simplify:
End do.
End if
Step 2: Compute and simplify:
Step 3: Use the DB-kDETGTRI algorithm to check the non-singularity of the coefficient matrix of the system (5).
Step 4: If the determinant of the coefficient matrix in (5) equals zero, then Exiterror (“No solutions”) End if.
Step 5: Compute the solution vector

For

Compute and simplify:
End do.
Step 6: For

Compute and simplify:
End do.
For

Compute and simplify:
End do.
Step 7: Substitute

Concerning the computational cost of Algorithm 3.2, we have: For






Remarks:
・ The DB-kTRI2 algorithm is a natural generalization of the algorithms in [30] and [34] .
・ The last component,

・ The last component,

A MAPLE procedure, based on the algorithm DB-kDETGTRI and DB-kTRI2, is available upon request from the authors.
4. Illustrative Examples
Example 4.1. Solve the bordered k-tridiagonal linear system
Solution: We have:







By applying the DB-kTRI1 algorithm, we get
・
・


・


・

・ The solution vector is

Example 4.2. Solve the bordered k-tridiagonal linear system
Solution: We have:






By applying the DB-kTRI2 algorithm, we have
・
・


・ The solution vector is
Example 4.3. Solve the bordered k-tridiagonal linear system
Solution: We have:







By applying the DB-kTRI1 algorithm, we get
・
・


・


・

・ The solution vector is

By applying the DB-kTRI2 algorithm, we have
・
・


・ The solution vector is

5. Conclusion
In this paper we have derived two symbolic algorithms (DB-kTRI1 and DB-kTRI2) for solving bordered k- tridiagonal linear systems. The cost of each algorithm is
Cite this paper
MoawwadEl-Mikkawy,FaizAtlan, (2015) New Algorithms for Solving Bordered k-Tridiagonal Linear Systems. Journal of Applied Mathematics and Physics,03,862-873. doi: 10.4236/jamp.2015.37107
References
- 1. El-Mikkawy, M.E.A. (2004) A Fast Algorithm for Evaluating nth Order Tri-Diagonal Determinants. Journal of Computational and Applied Mathematics, 166, 581-584.
http://dx.doi.org/10.1016/j.cam.2003.08.044 - 2. El-Mikkawy, M.E.A. and Karawia, A. (2006) Inversion of General Tridiagonal Matrices. Applied Mathematics Letters, 19, 712-720. http://dx.doi.org/10.1016/j.aml.2005.11.012
- 3. Akin, H. (2012) On 1D Reversible Cellular Automata with Reflective Boundary over the Prime Field of Order p. International Journal of Modern Physics C, 23, 1-13.
http://dx.doi.org/10.1142/s0129183111017020 - 4. Chant, T.F. and Resascot, D.C. (1986) Generalized Deflated Block-Elimination. SIAM Journal on Numerical Analysis, 23, 913-924. http://dx.doi.org/10.1137/0723059
- 5. El-Mikkawy, M.E.A. (1991) An Algorithm for Solving Tridiagonal Systems. Journal of Institute of Mathematics and Computer Sciences. Computer Sciences Series, 4, 205-210.
- 6. El-Mikkawy, M.E.A. (2003) A Note on a Three-Term Recurrence for a Tridiagonal Matrix. Applied Mathematics and Computation, 139, 503-511. http://dx.doi.org/10.1016/S0096-3003(02)00212-6
- 7. El-Mikkawy, M.E.A. (2004) On the Inverse of a General Tridiagonal Matrix. Applied Mathematics and Computation, 150, 669-679. http://dx.doi.org/10.1016/S0096-3003(03)00298-4
- 8. El-Mikkawy, M.E.A. (2005) A New Computational Algorithm for Solving Periodic Tri-Diagonal Linear Systems. Applied Mathematics and Computation, 161, 691-696.
http://dx.doi.org/10.1016/j.amc.2003.12.114 - 9. El-Mikkawy, M.E.A. and Rahmo, E.-D. (2008) A New Recursive Algorithm for Inverting General Tridiagonal and Anti-Tridiagonal Matrices. Applied Mathematics and Computation, 204, 368-372.
http://dx.doi.org/10.1016/j.amc.2008.06.053 - 10. El-Mikkawy, M.E.A. and Rahmo, E.-D. (2009) A New Recursive Algorithm for Inverting General Periodic Pentadiagonal and Anti-Pentadiagonal Matrices. Applied Mathematics and Computation, 207, 164-170.
http://dx.doi.org/10.1016/j.amc.2008.10.010 - 11. El-Mikkawy, M.E.A. and Rahmo, E. (2010) Symbolic Algorithm for Inverting Cyclic Pentadiagonal Matrices Recursively—Derivation and Implementation. Computers & Mathematics with Applications, 59, 1386-1396. http://dx.doi.org/10.1016/j.camwa.2009.12.020
- 12. El-Mikkawy, M.E.A. (2012) A Generalized Symbolic Thomas Algorithm. Applied Mathematics, 3, 342-345.
http://dx.doi.org/10.4236/am.2012.34052 - 13. Kavcic, A. and Moura, J.M.F. (2000) Matrices with Banded Inverses: Inversion Algorithms and Factorization of Gauss-Markov Processes. IEEE Transactions on Information Theory, 46, 1495-1509.
http://dx.doi.org/10.1109/18.954748 - 14. Li, H.B., Huang, T.Z., Liu X.P. and Li, H. (2010) On the Inverses of General Tridiagonal Matrices. Linear Algebra and Its Applications, 433, 965-983. http://dx.doi.org/10.1016/j.laa.2010.04.042
- 15. Shapiro, L.W. (1984) Positive Definite Matrices and Catalan Numbers, Revisited. Proceedings of the American Mathematical Society, 90, 488-496. http://dx.doi.org/10.1090/S0002-9939-1984-0728375-5
- 16. Sogabe, T. (2007) On a Two-Term Recurrence for the Determinant of a General Matrix. Applied Mathematics and Computation, 187, 785-788. http://dx.doi.org/10.1016/j.amc.2006.08.156
- 17. Sugimoto, T. (2012) On an Inverse Formula of a Tridiagonal Matrix. Operators and Matrices, 6, 465-480.
http://dx.doi.org/10.7153/oam-06-30 - 18. Usmani, R. (1994) Inversion of a Tridiagonal Jacobi Matrix. Linear Algebra and Its Applications, 212/213, 413-414. http://dx.doi.org/10.1016/0024-3795(94)90414-6
- 19. Akbudak, K., Kayaaslan, E. and Aykanat, C. (2012) Analyzing and Enhancing OSKI for Sparse Matrix-Vector Multiplication. www.prace-ri.eu
- 20. Amodio, P., Gladwelly, I. and Romanazzi, G. (2006) Numerical Solution of General Bordered ABD Linear Systems by Cyclic Reduction. Journal of Numerical Analysis, Industrial and Applied Mathematics, 1, 5-12.
- 21. Doedel, E. (1991) Numerical Analysis and Control of Bifurcation Problems (I): Bifurcation in Finite Dimensions. International Journal of Bifurcation and Chaos in Applied Sciences and Engineering, 1, 493-520. http://dx.doi.org/10.1142/S0218127491000397
- 22. Duff, I.S. and Scott, J.A. (2004) Stabilized Bordered Block Diagonal Forms for Parallel Sparse Solvers, RAL-TR-2004-006. http://www.numerical.rl.ac.uk/reports/reports.html
- 23. da Fonseca, C.M. (2006) A Note on the Inversion of Acyclic Matrices. International Journal of Pure and Applied Mathematics, 31, 307-317.
- 24. Martin, A. and Boyd, I.D. (2010) Variant of the Thomas Algorithm for Opposite-Bordered Tridiagonal Systems of Equations. International Journal for Numerical Methods in Biomedical Engineering, 26, 752-759. http://dx.doi.org/10.1002/cnm.1172
- 25. Pajic, S. (2007) Power System State Estimation and Contingency Constrained Optimal Power Flow a Numerically Robust Implementation. PhD Thesis, Worcester-Polytechnic Institute, Worcester.
- 26. Rashidinia, J. and Jalilian, R. (2009) Non-Polynomial Spline Solution of Fourth-Order Obstacle Boundary-Value Problems. World Academy of Science, Engineering and Technology. International Scholarly and Scientific Research & Innovation, 3, 167-173.
- 27. Udala, A., Reedera, R., Velmrea, E. and Harrisonb, P. (2006) Comparison of Methods for Solving the Schrodinger Equation for Multiquantum Well Heterostructure Applications. Proceedings of the Estonian Academy of Sciences, Engineering, 12, 246-261.
- 28. Wang, X.B. (2009) A New Algorithm with Its Scilab Implementation for Solution of Bordered Tridiagonal Linear Equations. 2009 IEEE International Workshop on Open-Source Software for Scientific Computation (OSSC), Guiyang, 18-20 September 2009, 11-14.
- 29. Golub, G. and Van Loan, C. (1996) Matrix Computations. Third Edition, The Johns Hopkins University Press, Baltimore and London.
- 30. El-Mikkawy, M.E.A. and Atlan, F. (2014) Algorithms for Solving Doubly Bordered Tridiagonal Linear Systems. British Journal of Mathematics & Computer Science, 4, 1246-1267.
http://dx.doi.org/10.9734/BJMCS/2014/8835 - 31. Burden, R.L. and Faires, J.D. (2001) Numerical Analysis. Seventh Edition, Books & Cole Publishing, Pacific Grove.
- 32. Karawia, A.A. (2013) Symbolic Algorithm for Solving Comrade Linear Systems Based on a Modified Stair-Diagonal Approach. Applied Mathematics Letters, 26, 913-918.
http://dx.doi.org/10.1016/j.aml.2012.10.019 - 33. Karawia, A.A. (2012) A New Recursive Algorithm for Inverting a General Comrade Matrix. CoRR abs/1210.4662.
- 34. Karawia, A.A. and Rizvi, Q.M. (2013) On Solving a General Bordered Tridiagonal Linear System. International Journal of Mathematics and Mathematical Sciences, 33, 1160-1163.
NOTES
*Corresponding author.





































