Journal of Applied Mathematics and Physics
Vol.02 No.09(2014), Article ID:49147,5 pages
10.4236/jamp.2014.29100
A Numerical Method for Singular Boundary-Value Problems
Abdalkaleg Hamad1, M. Tadi1, Miloje Radenkovic2
1Department of Mechanical Engineering, University of Colorado at Denver, Denver, USA
2Department of Electrical Engineering, University of Colorado at Denver, Denver, USA
Email: mohsen.tadi@ucdenver.edu, Miloje.Radenkovic@ucdenver.edu
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 June 2014; revised 10 July 2014; accepted 23 July 2014
ABSTRACT
This note is concerned with an iterative method for the solution of singular boundary value problems. It can be considered as a predictor-corrector method. Sufficient conditions for the convergence of the method are introduced. A number of numerical examples are used to study the applicability of the method.
Keywords:
Singular Boundary-Value Problem, Singularly Perturbed Boundary Value Problem

1. Introduction
In this note we consider a numerical method for singular linear boundary value problems. Such problems arise very naturally in various applications including gas dynamics, chemical reactions, and structural mechanics. Traditional methods fail to produce good approximations for such equations. As a result, a number of investigators have considered various non-classical methods, including Chebyshev polynomials, B-splines, and cubic splines [1] -[3] . Recent results also include methods based on reproducing kernel space [4] [5] , and Sinc collocation method [6] .
The purpose of this note is to develop an iterative method for singular and singularly perturbed boundary value problems. The method is explicit in nature, and can be considered to be an iterative predictor-corrector method. Section 2 introduces the method in details. Section 3 provides sufficient conditions for the convergence of the method. Section 4 uses a number of examples to investigate the applicability of the method, and compares the results to exact solutions.
2. An Iterative Method for a Singular Boundary Value Problem
Consider a second-order singular differential equation given by
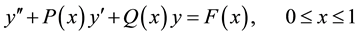 (1)
(1)
With Dirichlet-type boundary condition
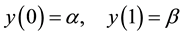 (2)
(2)
where, the functions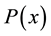 ,
, 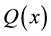 and
and 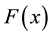 are analytic in
are analytic in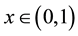 . The functions
. The functions 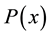 and
and 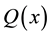 can vanish at the boundary points. Assume that the domain is divided into
can vanish at the boundary points. Assume that the domain is divided into 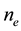 equal intervals
equal intervals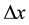 , which leads to
, which leads to 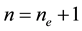 nodes with
nodes with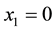 ,
, 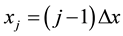 , for
, for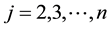 . The boundary conditions provide the values for
. The boundary conditions provide the values for 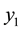 and
and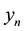 . Consider a finite difference approximation of the above equation given by
. Consider a finite difference approximation of the above equation given by
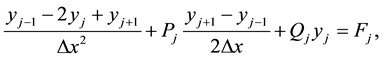
where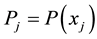
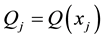
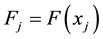
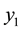
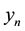
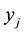

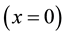
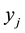
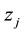
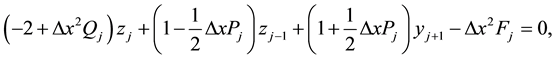
for
Note that, marching from the left to right, the above equation is explicit for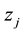
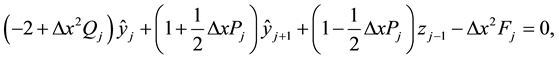
For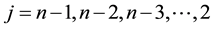
The variable 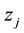
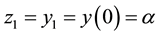
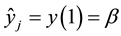
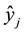
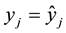
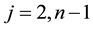
3. Convergence of the Method
For simplicity, consider a second-order singular differential equation given by
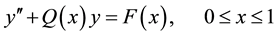
The same analysis can be performed for a non-zero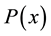
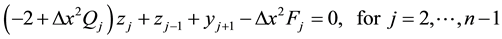
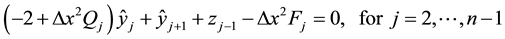
In a matrix form, the first step can be written as
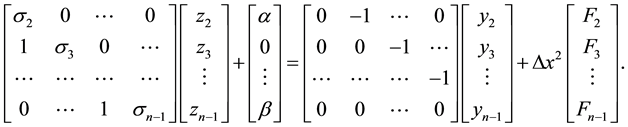
where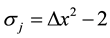
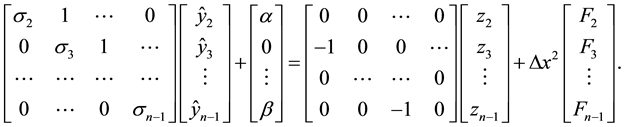
The above equations can be written in a more compact form according to
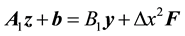
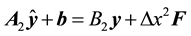
where, the bold lower case letters indicate vectors corresponding to the above terms. After eliminating the intermediate term 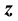
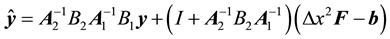
For convergence of the above iteration, it is sufficient that all eigenvalues of the coefficient matrix, i.e.,
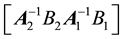
explicit expressions for the inverses. For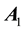
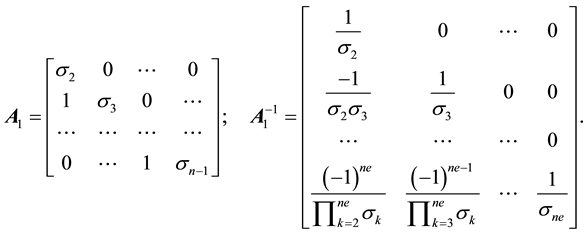
Note that matrix 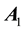
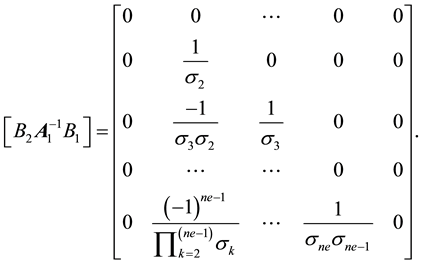
The matrix 
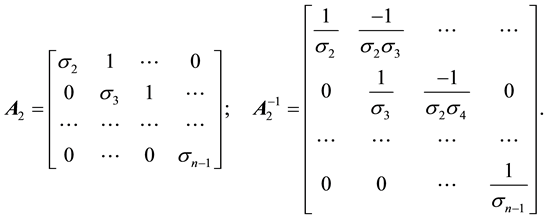
Writing the coefficient matrix in Equation (13) as a product of two matrices according to
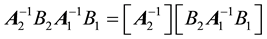
The first matrix on the right hand side is upper triangular, and the second matrix is lower triangular. The diagonal entries are the eigenvalues and using the spectral radius, it is sufficient to have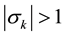
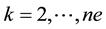
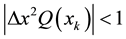
of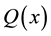
4. Numerical Examples
Example 1: Consider a singular boundary value problem [4] given by
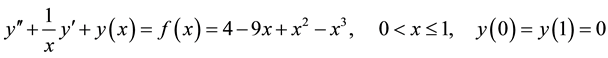
The exact solution is given by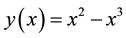
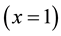
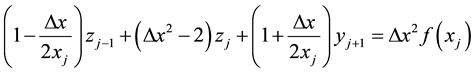
The second step is to march back from 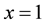
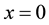
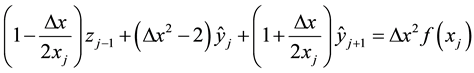
Both steps involve the explicit calculations only. After dividing the domain into equal intervals, Table 1 presents the results at selected points inside the domain and compares their values to the exact solution. The iterations are continued until the results do not change. In all the cases, the error is within the order of the approximation of the finite difference scheme. The relative error in the table is computed according to
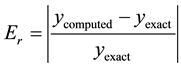
Example 2: Consider another singular boundary value problem [7] given by
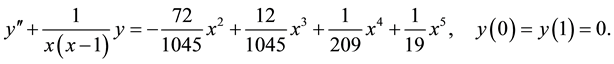
The exact solution is given by
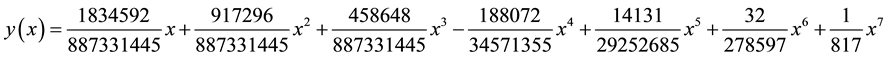
Dividing the domain into equal intervals and using the above method, Table 2 compares the computed solution with the exact solution at different points in the domain. The computed values are after 90,000 iterations. But the calculations are explicit and pose little burden.
Example 3: Consider a singularly perturbed boundary-value problem [7] given by
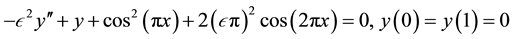
for which the exact solution is given by
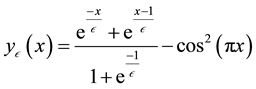
This problem is singularly perturbed, and large gradients exist close to the boundaries. The present method can still be used to obtain an accurate solution. Table 3 presents the convergence of the solution close to the left 
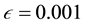
The above results are for finite difference approximation with equal intervals. The accuracy of the results can be improved by using a smaller mesh sizes close to the boundaries. However, the calculations are explicit and using equal intervals does not pose a computational burden.
5. Conclusions
In this note we presented a numerical method for obtaining the solution of linear singular boundary value prob-
Table 1. Computed value and the relative error at different values of x.
Table 2. Computed value and the relative error at different values of x for Example 2.
Table 3. Computed values and comparison to the exact solution close to x = 0.
Table 4. Computed values and comparison to the exact solution close to x = 1.
lems. The method can be considered as an iterative predictor-corrector method. Sufficient conditions for the convergence of the iteration was also presented. The proposed method is fully explicit and requires little computational time. It can also be applied to singularly perturbed boundary value problems.
Three numerical examples were used to study the applicability of the method.
References
- Kadalbajoo, M. and Agarwal, V. (2004) Cubic Spline for Solving Singular Two-Point Boundary Value Problems. Applied Mathematics and Computation, 156, 249-259. http://dx.doi.org/10.1016/j.amc.2003.07.020
- Ravi Kanth, A. and Reddy, Y. (2005) Cubic Spline for a Class of Singular Two Point Boundary Value Problems. Applied Mathematics and Computation, 170, 733-740. http://dx.doi.org/10.1016/j.amc.2004.12.049
- Mohanty, R.K., Sachder, P.L. and Jha, N. (2004) An o(h4) Accurate Cubic Spline TAGE Method for Nonlinear Singu- lar Two Point Boundary Value Problem. Applied Mathematics and Computation, 158, 853-868. http://dx.doi.org/10.1016/j.amc.2003.08.145
- Geng, F.Z. and Cui, M.G. (2007) Solving Singular Nonlinear Second-Order Periodic Boundary Value Problems in the Reproducing Kernel Space. Applied Mathematics and Computation, 192, 389-398. http://dx.doi.org/10.1016/j.amc.2007.03.016
- Li, Z.Y., Wang, Y.L., Tan, F.G., Wan, X.H. and Nie, T.F. (2012) The Solution of a Class of Singularly Perturbed Two-Point Boundary Value Problems by the Iterative Reproducing Kernel Method. Abstract and Applied Analysis, 1-7.
- Mohsen, A. and El-Gamel, M. (2008) On the Galerkin and Collocation Methods for Two-Point Boundary Value Prob- lems Using Sinc Bases. Computers and Mathematics with Allications, 56, 930-941. http://dx.doi.org/10.1016/j.camwa.2008.01.023
- Secer, A. and Kurulay, M. (2012) The Sinc-Galerkin Method and Its Applications on Singular Dirichlet-Type Boun- dary Value Problems. Boundary Value Problems, 126, 1-14.