Journal of Applied Mathematics and Physics
Vol.2 No.8(2014), Article
ID:47409,8
pages
DOI:10.4236/jamp.2014.28082
Proximity Effect in Normal-Superconductor Hybrids at the Nanoscale
Henning Soller
Institut für Theoretische Physik, Universität Heidelberg, Heidelberg, Germany
Email: hsoller@googlemail.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 April 2014; revised 22 May 2014; accepted 3 June 2014
ABSTRACT
We analyse the proximity effect in hybrid nanoscale junctions involving superconducting leads. We develop a general framework for the analysis of the proximity effect using the same theoretical methods typically employed for the analysis of conductance properties. We apply our method to a normal-superconductor tunnel contact and compare our results to previous results.
Keywords:Superconductors, Proximity Effect, Hybrid Nanoscale Junctions, Conductance

1. Introduction
Recently there has been significant progress both experimentally and theoretically in the study of hybrid nanoscale junctions involving superconductors [1] -[3] due to the possibility of transfer of electron pairs from superconductors to differently ordered materials. If the superconductor is attached to two (e.g. normal conducting) leading the Cooper pairs from the superconductor may split and form an entangled electron pair via the process of crossed Andreev reflection [4] .
The possibility of generating entanglement by such transfers is the building block for future quantum computational applications of superconductor hybrids and has been successfully demonstrated experimentally [5] [6] . However, the underlying physical details are still not completely understood since many experimental setups involve complicated setups not using superconductors directly but using the proximity effect of superconducting correlations [5] [6] . So far the focus of most theoretical studies has been transport properties of such structures in non-equilibrium [7] . However, apart from the current also the induced gaps in the attached materials are measurable and provide valuable information about the transfer of electron pairs [8] .
In this work, we provide first steps towards understanding the proximity effect in superconductor hybrid structures by studying the proximity effect in a normal-superconductor junction at low transparency using the same technical formalism as for typical studies of transport properties [9] [10] . A typical setup of a normal-superconductor quantum point contact (NS QPC) is illustrated in Figure 1.
We compute the full spatial development of the induced gaps close to the superconductor-normal conductor interface and compare them to other studies of similar junctions using a different approach.
The paper is structured as follows: in Chapter 2 we describe the similarity of BCS-theory and induced superconductivity in order to derive a gap equation for the anomalous Green’s functions. We calculate the latter in Chapter 3 and derive the gaps in the superconductor and in the normal conductor. In Chapter 4 we perform the calculation of the spatial development of the gap and compare our results to a different approach in Chapter 5. We conclude in Chapter 6.
2. Correspondence to Strongly Coupling Theory
We study a one-dimensional contact between a superconductor and a normal conductor, meaning that we assume that the contact area between both materials is small enough and the spatial restrictions such that the system can be effectively considered one-dimensional as far as the interface is concerned.
This description can be easily enhanced to systems with larger extension along the direction normal to the interface, since these would correspond to several instances of the below mentioned system with the assumption that these transport channels do not interact [11] [12] . If the transport channels interact the result will be different, e.g. fractal scaling in the spectrum of such structures has been observed [13] .
In the case of the present work the system can be described by the following Hamiltonian
 (1)
(1)
H1 refers to the normal metal which is modelled as a non-interacting fermionic continuum at a chemical potential μ1, written in terms of electron field operators 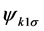 with density of states at the Fermi level
with density of states at the Fermi level![]() . H2 refers to the superconductor that is described by the BCS Hamiltonian with the gap Δ assumed to be real
. H2 refers to the superconductor that is described by the BCS Hamiltonian with the gap Δ assumed to be real
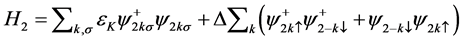 (2)
(2)
As in typical treatments of superconductor-hybrid structures we keep the superconductor at 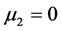 so that the bias voltage
so that the bias voltage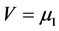 . The superconducting energy gap leads to an energy dependent gap in the density of states close to the Fermi level which is given by
. The superconducting energy gap leads to an energy dependent gap in the density of states close to the Fermi level which is given by
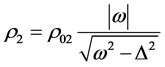 (3)
(3)
Tunneling between the two electrodes is assumed to occur locally (at x = 0) and the corresponding Hamiltonian is given by [14]
 (4)
(4)
We solve the corresponding Dyson equations using the Hamiltonian approach [10] , meaning that we calculate the full Green’s functions characterizing the Hamiltonian using units such that .
.
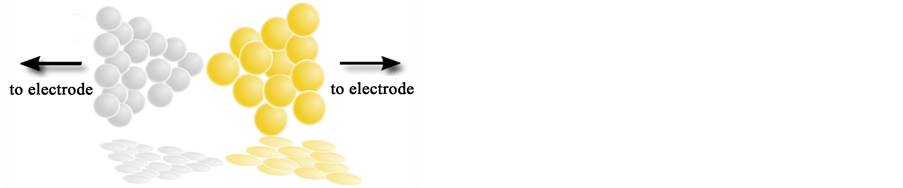
Figure 1. Illustration of a typical point-contact geometry. The superconductor (light grey) is contacted to a normal metal such that the contact area is on the nanoscale and the spatial restrictions are such that the system can be considered one-dimensional.
The emerging Feynman Dyson equations for the full Green’s functions for the normal conducting electrode include 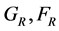 and
and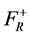 , meaning the normal and the two anomalous Green’s functions.
, meaning the normal and the two anomalous Green’s functions.
In the presence of external magnetic fields the treatment will be different. In this case we would have to include the effect of a magnetic field via the Usadel equation and obtain the necessary Green’s functions from it [15] . In this work we will not include external fields.
Their corresponding Dyson equations have been illustrated in Figure 2.
The structure of the Green’s function can now be compared to the Green’s functions of strong coupling theory [16] .
The strong coupling theory is applicable to superconductors for which the electron-phonon coupling is quite strong and hence the BCS theory is not a good description. Instead the starting point for the strong coupling theory is an effective interaction including a screened Coulomb interaction as well as a screened phonon interaction. The Matsubara GFs are calculated self-consistently including the phonon-interaction by an effective potential. The Dyson equations are illustrated in Figure 3 where the effective interaction is drawn as an arc with an arrow underneath. The self-energies are named S and W. The normal GF is drawn as a dashed arrow and the full GFs are again indicated by a doubled line.
The Dyson equations look very similar to those obtained for the NS QPC. Indeed the Dyson equations are of the above type for all typical normal-superconductor hybrids (e.g. involving quantum dots [4] [17] [18] , ferromagnets [19] [20] [21] or Majorana fermions [22] ). The self-energies S and W, respectively correspond to the self-energies by the normal and the anomalous GF of the superconducting electrode in the case of NS QPCs. This correspondence allows us to derive a gap equation for both sides of the normal-superconductor junction and to derive the local value of the pairing gap.
3. Gap Equation
Due to the strong similarity between strong coupling theory and the theory of NSQPCs as obtained from the comparison of the corresponding Dyson equations it is also be possible to derive the gap structure at x = 0 like in strong coupling theory.
The superconducting gap may be derived from the retarded anomalous equal time Green’s function (mind the appropriate normalization of the Fourier transform)

Figure 2. Illustration of the Feynman diagrams corresponding to the Dyson equation for the normal-superconductor, point contact. The single solid lines represent the superconducting normal and anomalous Green’s functions and the dotted lines represent the normal conducting Green’s function. The double lines represent the exact-in-tunneling Green’s functions for the normal electrode. An anomalous Green’s function emerges due to the presence of the superconductor.
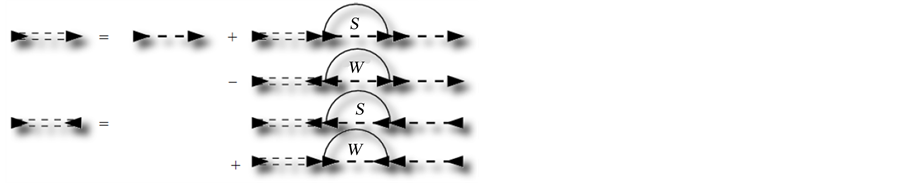
Figure 3. Sketch of the emerging Green’s functions in strong coupling theory.
 (5)
(5)
We only evaluated the retarded anomalous GF for the normal and superconducting side using the approximation of small interface transparency illustrated in [18] in order to simplify the emerging expressions. The full expressions can also be used but analytical progress is limited to numerical evaluations.
The corresponding simplified retarded GFs without coupling are given in [23] [24] . From them we calculate the GFs including the tunnel coupling to the other lead and acquire the following expression for the superconducting gap induced on the normal side (energies measured in units of ∆)
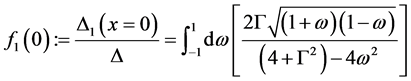 (6)
(6)
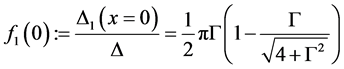 (7)
(7)
The abbreviation 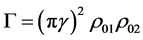 can be regarded as the transparency of the tunneling contact. The appearing superconducting gap on the normal side is often referred to as the minigap [25] . For the superconducting side the expression becomes
can be regarded as the transparency of the tunneling contact. The appearing superconducting gap on the normal side is often referred to as the minigap [25] . For the superconducting side the expression becomes
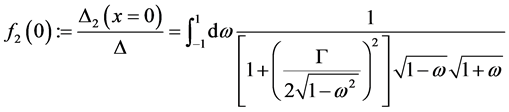 (8)
(8)
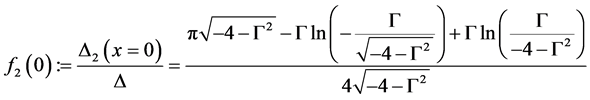 (9)
(9)
The expressions f1(0) and f2(0) are therefore obtained directly from the corresponding GFs including tunneling. They correspond to the pairing potential (or energy gap) close to the interface in the normal conducting side and the superconducting side. One observes that the pairing potential at the interface in the superconductor is reduced due to the presence of the normal conductor.
It can be seen from Equation (7) and Equation (9) that the superconducting gaps do not depend on voltage and temperature explicitely. Both gaps are fixed around the chemical potential of the superconductor at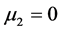 . This means that, if the voltage on the normal side is driven above or below the minigap, no minigap will be observed.
. This means that, if the voltage on the normal side is driven above or below the minigap, no minigap will be observed.
The only temperature dependence originates from the temperature dependence of the bulk gap value ∆. So far this temperature dependence was not discussed as energies were only considered when normalized to the gap. The dependence of ∆ on temperature is given by the Thouless formula [26]
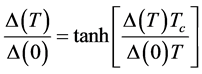 (10)
(10)
where T refers to the temperature of the experiment in question and Tc refers to the critical temperature of the bulk superconductor.
Equation (10) in turn also means that the critical temperature for the observation of the proximity effect is the same as for the observation of superconductivity in the bulk superconductor.
4. Induced Superconductivity
From Equation (7) and Equation (9) it is obvious that the superconducting order parameter at an NS interface extends into the normal metal. This behavior is well-known [27] and the spatial extension of the minigap into the normal conductor as well as the spatial extension of the suppression of the gap in the superconductor have been the subject of intense research [28] .
Changes of the order parameter can be described by the Ginzburg-Landau equation [29] that reads at zero magnetic field and in one dimension
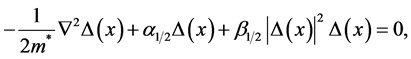 (11)
(11)
where the phenomenological parameters α and β can take two different values depending on whether we are in the normal conducting or the superconducting side. The solution for a constant order parameter is either 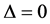
(normal conductor) or 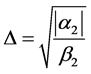 for
for 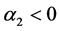 and
and 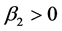 as it must be for a non-vanishing order parameter in the superconductor. We introduce a dimensionless function
as it must be for a non-vanishing order parameter in the superconductor. We introduce a dimensionless function 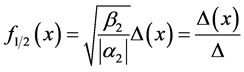 (again depending on which side of the junction is considered) so that Equation (11) can be rewritten as
(again depending on which side of the junction is considered) so that Equation (11) can be rewritten as
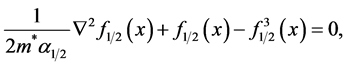 (12)
(12)
The emerging characteristic length scale for the problem is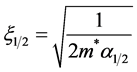 , also known as the GinzburgLandau length.
, also known as the GinzburgLandau length.
We solve the Ginzburg-Landau equation in the superconductor and in the normal metal using boundary conditions at x = 0 derived before (see Equation (7) and Equation (9)) and the obvious boundary conditions that
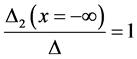 ,
, .
.
The solution for the superconducting side is
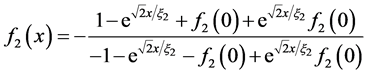 (13)
(13)
For the normal conducting side we obtain
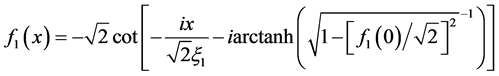 (14)
(14)
Both solutions taken together allow the gap to be calculated as a function of x and the parameters ξ1/2. Mind that the above solution is fully analytic not involving numerical calculations.
5. Comparison with Known Results
The gap equation in infinite NS double layer systems (not quantum point contacts) has been considered [30] using a quasi classical GF theory [31] . However, the derivation in [30] uses an energy independent reflection coefficient and a self-consistent pair potential to describe the spatial development and the boundary conditions for at the interface.
In [30] the gap is calculated numerically as a function of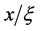 , where ξ is the coherence length of the superconductor and ξ1/2 are expressed as multiples of this value. The calculation is done for a fixed value of the reflection coefficient. We use the results in Equation (13) and Equation (14) and fit in order to obtain the same result. Both results are shown in Figure 4.
, where ξ is the coherence length of the superconductor and ξ1/2 are expressed as multiples of this value. The calculation is done for a fixed value of the reflection coefficient. We use the results in Equation (13) and Equation (14) and fit in order to obtain the same result. Both results are shown in Figure 4.
A small discrepancy is observed for the normal conducting side. This can be attributed to the fact that the two systems in question are different leading to slightly different behaviors in the decay of the superconducting amplitude on the normal side.
However, the agreement between the theoretical calculation in [30] and the results from Equation (13) and Equation (14) is quite good. Especially the order parameter has a jump at the interface as predicted in [32] . Thus it seems legitimate to make a prediction for the evolution of the gap as a function of  and x by using Equation (13) and Equation (14) as shown in Figure 5.
and x by using Equation (13) and Equation (14) as shown in Figure 5.
We observe the typical jump of the order parameter at the interface and the reduction of the superconducting order parameter at the interface to the normal conductor. The normal conductor acquires an order parameter over a considerable length scale via the proximity effect.
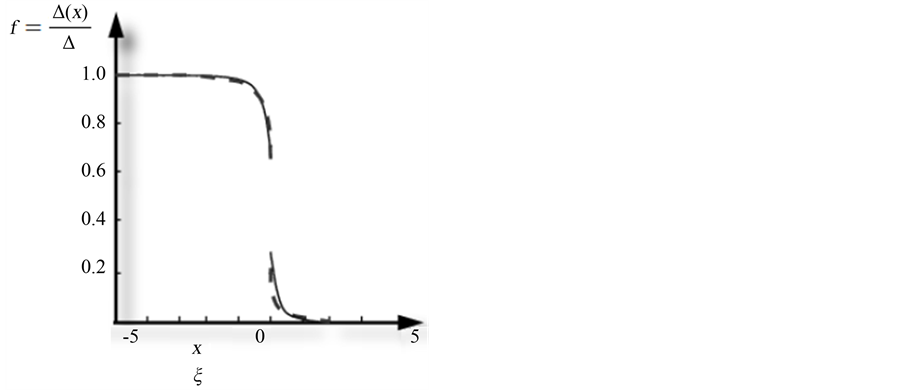
Figure 4. The result from Equation (13) and Equation (14) is shown as the solid line using parameters![]() ,
, ![]() and
and . The result is compared to the result from [26] for R = 0.5 shown as the dashed curve.
. The result is compared to the result from [26] for R = 0.5 shown as the dashed curve.
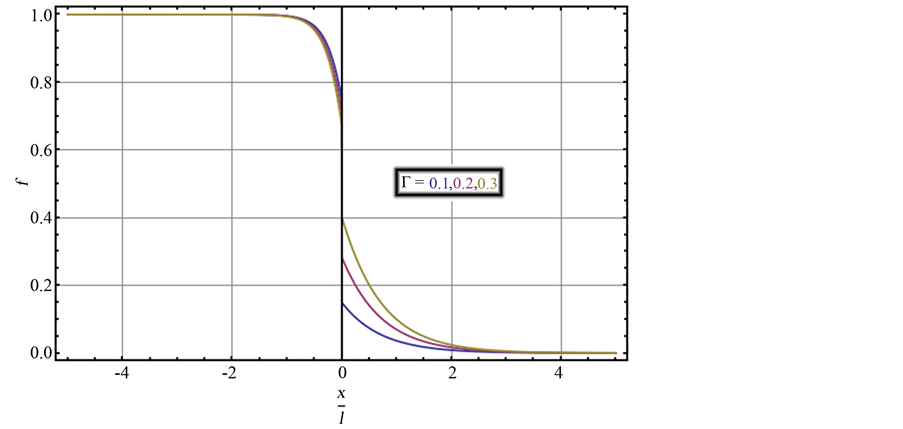
Figure 5. Superconducting gap in the superconducting (left) and normal conducting (right) electrode as a function of 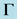 and x/l for coherence lengths
and x/l for coherence lengths![]() ,
, ![]() with a characteristic length scale l for different values of Γ corresponding to the lower, middle and upper curve.
with a characteristic length scale l for different values of Γ corresponding to the lower, middle and upper curve.
6. Conclusion
To conclude, we have calculated the Green’s functions at the interface in a normal-superconductor hybrid setup and obtained the resulting gap equation that can be applied for general hybrid superconductor junctions. We calculated the gap for a typical normal-superconductor tunnel junction and analysed the spatial gap dependence using the Ginzburg-Landau formalism. We compared our results to previous results and obtained good agreement.
Acknowledgements
The author would like to thank A. Komnik, S. Maier and J. Dahlhaus for numerous discussions.
References
- Hofstetter, L., Csonka, S., Nygard, J. and Schonenberger, C. (2009) Cooper Pair Splitter Realized in a Two-QuantumDot Y-Junction. Nature, 461, 960-963. http://dx.doi.org/10.1038/nature08432
- Machon, P., Eschrig, M. and Belzig, W. (2013) Nonlocal Thermoelectric Effects and Nonlocal Onsager Relations in a Three-Terminal Proximity-Coupled Superconductor-Ferromagnet Device. Physical Review Letters, 110, 047002. http://dx.doi.org/10.1103/PhysRevLett.110.047002
- Das, A., Ronen, Y., Heiblum, M., Mahalu, D., Kretinin, A.V. and Shtrikman, H. (2012) High-Efficiency Cooper Pair Splitting Demonstrated by Two-Particle Conductance Resonance and Positive Noise Cross-Correlation. Nature Communication, 3, 1165.
- Borlin, J., Belzig, W. and Bruder, C. (2002) Full Counting Statistics of a Superconducting Beam Splitter. Physical Review Letters, 88, 197001. http://dx.doi.org/10.1103/PhysRevLett.88.197001
- Schindele, J., Baumgartner, A. and Schonenberger, C. (2012) Near-Unity Cooper Pair Splitting Efficiency. Physical Review Letters, 109, 157002. http://dx.doi.org/10.1103/PhysRevLett.109.157002
- Hofstetter, L., Csonka, S., Baumgartner, A., Fülop, G., d’Hollosy, S., Nygard, J. and Schonenberger, C. (2011) FiniteBias Cooper Pair Splitting. Physical Review Letters, 107, 136801. http://dx.doi.org/10.1103/PhysRevLett.107.136801
- Muzykantskii, B.A. and Khmelnitskii, D.E. (1994) Quantum Shot Noise in a Normal-Metal-Superconductor Point Contact. Physical Review B, 50, 3982-3987. http://dx.doi.org/10.1103/PhysRevB.50.3982
- De Franceschi, S., Kouwenhoven, L., Schonenberger, C. and Wernsdorfer, W. (2010) Hybrid Superconductor-Quantum Dot Devices. Nature Nanotechnology, 5, 703-711. http://dx.doi.org/10.1038/nnano.2010.173
- Soller, H. and Komnik, A. (2011) Hamiltonian Approach to the Charge Transfer Statistics of Kondo Quantum Dots Contacted by a Normal Metal and a Superconductor. Physica E, 44, 425-429. http://dx.doi.org/10.1016/j.physe.2011.09.014
- Cuevas, J.C., Martin-Rodero, A. and Levy Yeyati, A. (1996) Hamiltonian Approach to the Transport Properties of Superconducting Quantum Point Contacts. Physical Review B, 54, 7366. http://dx.doi.org/10.1103/PhysRevB.54.7366
- Zawadowski, A. (1967) General Theory of Tunneling in Oxide Diodes. Physical Review, 163, 341. http://dx.doi.org/10.1103/PhysRev.163.341
- Cluckie, J. and Barker, J.R. (1994) Two-Body Quantum Transport Theory of Interacting Electrons in Laterally Patterned Semiconductor 2DEG Structures. Semiconductor Science Technology, 9, 911. http://dx.doi.org/10.1088/0268-1242/9/5S/142
- Ossipov, A. and Kottos, T. (2004) Superconductor-Proximity Effect in Hybrid Structures: Fractality versus Chaos. Physical Review Letters, 92, 017004. http://dx.doi.org/10.1103/PhysRevLett.92.017004
- Cohen, M.H., Falicov, L.M. and Phillips, J.C. (1962) Superconductive Tunneling. Physical Review Letters, 8, 316-318. http://dx.doi.org/10.1103/PhysRevLett.8.316
- Pérez-Willard, F., Cuevas, J.C., Sürgers, C., Pfundstein, P., Kopu, J., Eschrig, M. and Lohneysen, H.V. (2004) Determining the Current Polarization in Al/Co Nanostructured Point Contacts. Physical Review B, 69, 140502(R). http://dx.doi.org/10.1103/PhysRevB.69.140502
- Eilenberger, G. (1968) Transformation of Gorkov’s Equation for Type II Superconductors into Transport-Like Equations. Z. Physics, 214, 195-213. http://dx.doi.org/10.1007/BF01379803
- Governale, M., Pala, M.G. and Konig, J. (2008) Real-Time Diagrammatic Approach to Transport through Interacting Quantum Dots with Normal and Superconducting Leads. Physical Review B, 77, 134513. http://dx.doi.org/10.1103/PhysRevB.77.134513
- Soller, H. and Komnik, A. (2011) Charge Transfer Statistics and Entanglement in Normal-Quantum Dot-Superconductor Hybrid Structures. European Physical Journal D, 63, 3-8. http://dx.doi.org/10.1140/epjd/e2010-00256-7
- Soller, H., Hofstetter, L., Csonka, S., Levy Yeyati, A., Schonenberger, C. and Komnik, A. (2012) Kondo Effect and Spin-Active Scattering in Ferromagnet-Superconductor Junctions. Physical Review B, 85, 174512. http://dx.doi.org/10.1103/PhysRevB.85.174512
- Benjamin, C. (2006) Crossed Andreev Reflection as a Probe for the Pairing Symmetry of Ferromagnetic Superconductors. Physical Review B, 74, 180503. http://dx.doi.org/10.1103/PhysRevB.74.180503
- Soller, H. and Komnik, A. (2012) P-Wave Cooper Pair Splitting. Beilstein Journal of Nanotechnology, 3, 493-500. http://dx.doi.org/10.3762/bjnano.3.56
- Nilsson, J., Akhmerov, A.R. and Beenakker, C.W.J. (2008) Splitting of a Cooper Pair by a Pair of Majorana Bound States. Physical Review Letters, 101, 120403. http://dx.doi.org/10.1103/PhysRevLett.101.120403
- Fazio, R. and Raimondi, R. (1998) Resonant Andreev Tunneling in Strongly Interacting Quantum Dots. Physical Review Letters, 80, 2913. http://dx.doi.org/10.1103/PhysRevLett.80.2913
- Soller, H. (2013) Non-Linear Transport Properties of Hybrid Nanoelectronic Devices. Logos Verlag Berlin GmbH, Berlin.
- Martin, T. (1996) Wave Packet Approach to Noise in NS Junctions. Physical Letters A, 220, 137-142. http://dx.doi.org/10.1016/0375-9601(96)00484-7
- Thouless, D.J. (1960) Strong-Coupling Limit in the Theory of Superconductivity. Physical Review, 117, 1256. http://dx.doi.org/10.1103/PhysRev.117.1256
- Smith, H.G. and Wilhelm, J.O. (1935) Superconductivity. Reviews of Modern Physics, 7, 237. http://dx.doi.org/10.1103/RevModPhys.7.237
- Hilsch, P. And Hilsch, R. (1961) Zum Verhalten von Supraleitern im Kontakt mit Normalleitern. Naturwissenschaften, 48, 549. http://dx.doi.org/10.1007/BF00639157
- Ketterson, J.B. and Song, S.N. (1999) Superconductivity. Cambridge University Press, Cambridge.http://dx.doi.org/10.1017/CBO9781139171090
- Nagato, Y., Nagai, K. and Hara, J.I. (1993) Theory of the Andreev Reflection and the Density of States in Proximity Contact Normal-Superconducting Infinite Double-Layer. Journal of Low Temperature Physics, 93, 33-56. http://dx.doi.org/10.1007/BF00682280
- Ashida, M., Hara, J.I. and Nagai, K. (1992) Superconducting Transition Temperature of Proximity-Contact Superconducting-Normal Double Layers. Physical Review B, 45, 828. http://dx.doi.org/10.1103/PhysRevB.45.828
- Zaitsev, A.V. (1984) Quasiclassical Equations of the Theory of Superconductivity for Contiguous Metals and the Properties of Constricted Microcontacts. Journal of Experimental and Theoretical Physics, 86, 1742-1758.

