Journal of Applied Mathematics and Physics
Vol.2 No.3(2014), Article ID:42743,11 pages DOI:10.4236/jamp.2014.23002
Determination of the Structural Constant of the Atom
Milan Perkovac*
The First Technical School TESLA, Zagreb, Croatia
Email: *milan@drivesc.com
Copyright © 2014 Milan Perkovac. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Milan Perkovac. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received December 11, 2013; revised January 10, 2014; accepted January 17, 2014
ABSTRACT
The equations for energy, momentum, frequency, wavelength and also Schrödinger equation of the electromagnetic wave in the atom are derived using the model of atom by analogy with the transmission line. The action constant A0 = (μ0/ε0)1/2s02e2 is a key term in the above mentioned equations. Besides the other well-known quantities, the only one unknown quantity in the last expression is a structural constant s0. Therefore, this article is dedicated to the calculation of the structural constant of the atoms on the basis of the above mentioned model. The structural constant of the atoms s0 = 8.277 56 shows up as a link between macroscopic and atomic world. After calculating this constant we get the theory of atoms based on Maxwell’s and Lorentz equations only. This theory does not require Planck constant h, which once was introduced empirically. Replacement for h is the action constant A0, which is here theoretically derived, while the replacement for fine structure constant α is 1/(2s02). In this way, the structural constant s0 replaces both constants, h and α. This paper also defines the stationary states of atoms and shows that the maximal atomic number is equal to 2s02 = 137.036, i.e., as integer should be Zmax=137. The presented model of the atoms covers three of the four fundamental interactions, namely the electromagnetic, weak and strong interactions.
Keywords: Action Constant; Fine Structure Constant; Lecher’s Line; Phase Velocity; Planck’s Constant; Stability of Atoms; Stationary States; Structural Coefficient; Structural Constant; Transmission Line
1. Introduction
Although for a long time classical physics and Maxwell’s equations were pushed out of research in the field of atomic phenomena, the article [1] showed that the equations of atom theory can be derived with the help of Maxwell’s and Lorentz equations in the classical way. Thus, we derived equations for energy, momentum, frequency and wavelength of an electromagnetic wave in an atom, which coincide with the corresponding equations in quantum mechanics. Moreover, we can derive Schrödinger wave equation as well. To achieve that, a new approach based on the classical theory is used. In that approach, an analogy between the electromagnetic wave in the atom and the wave of voltage and electric current in the transmission line plays a crucial role. The basic novelty of this approach is the introduction of a new concept of the so-called structural constant s0, which brings together both the parameters of transmission line (macro world) and the charge of the atoms (micro world). This article focuses on the calculation of a structural constant of the atom s0.
2. Model of an Atom
2.1. Atom and Transmission Line
According to [1], using Maxwell equations, electromagnetic wave in an atom is described by two partial differential equations of second order, the so-called wave equations [2]:
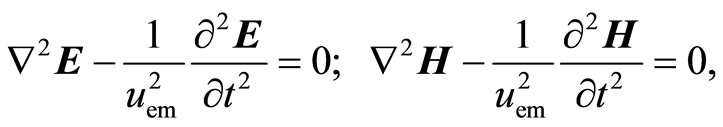 (1)
(1)
where vector E is the electric field strength, vector H is the magnetic field strength, 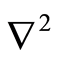 is del-squared (i.e., Laplace operator), t is time, and uem = λν is phase velocity of the electromagnetic wave in the atom, where λ is the wavelength and ν is the frequency of electromagnetic wave in the atom.
is del-squared (i.e., Laplace operator), t is time, and uem = λν is phase velocity of the electromagnetic wave in the atom, where λ is the wavelength and ν is the frequency of electromagnetic wave in the atom.
The same form of wave equations as (1), but only in one dimension, is also present on the parallel-wire transmission line (Lecher's line), consisting of a pair of ideal conductive nonmagnetic parallel wires of radius ρ, separated by δ, where the ratio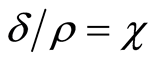 , [3]:
, [3]:
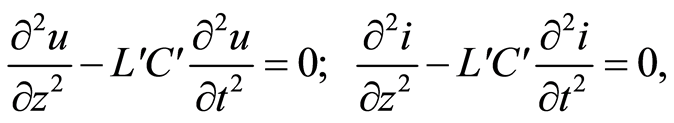 (2)
(2)
where u is voltage at the entrance of the element dz of Lecher's line, i is electric current at the entrance of the element dz of Lecher’s line, 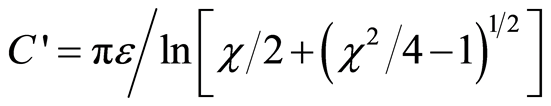 is capacitance of Lecher’s line per unit length,
is capacitance of Lecher’s line per unit length,
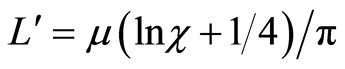 is inductance of Lecher's line per unit length, [4], ε is the permittivity of space in the atom, or in space of Lecher's line, and μ is the permeability of the space in the atom, or in the space of Lecher's line.
is inductance of Lecher's line per unit length, [4], ε is the permittivity of space in the atom, or in space of Lecher's line, and μ is the permeability of the space in the atom, or in the space of Lecher's line.
Systems with the same differential equations behave equally. Hence, in [1] it was concluded that the electric field in the atom behaves as the voltage on Lecher’s line, and the magnetic field in the atom behaves as the current in Lecher's line. Furthermore, [1] shows that the Lecher’s line may be represented as the inductive-capacitive network (so-called LC network), which finally makes the oscillatory circuit (LC circuit). The natural frequency of LC circuit , where C is the sum of all small capacitors of the LC network on the open end of the network, and L is sum of all small inductances of the LC network on the shortcircuited of the network [5].
, where C is the sum of all small capacitors of the LC network on the open end of the network, and L is sum of all small inductances of the LC network on the shortcircuited of the network [5].
2.2. Electromagnetic Energy in the Atom
According to the model presented in [1], electromagnetic energy in the atom Eem can be described as the electromagnetic energy of LC circuit, i.e.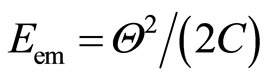 , where Θ is maximal charge on the said capacitor C, [6]. On the other hand, from the balance of forces in the atom follows [6]:
, where Θ is maximal charge on the said capacitor C, [6]. On the other hand, from the balance of forces in the atom follows [6]:
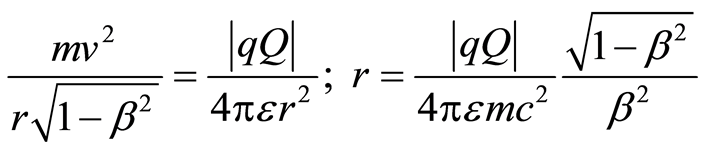 , (3)
, (3)
where r is the radius of the circular orbit of the electron, q is the charge of the electron (q = –e), e is elementary charge, Q is the charge of the nucleus (Q = Ze), Z is atomic number (which theoretically is not in integral domain), m is the electron rest mass, 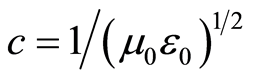 is the speed of light in vacuum,
is the speed of light in vacuum,  , where
, where 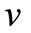 is the velocity of the electron, ε = εrε0, as stated above is permittivity, εr is relative permittivity, ε0 is permittivity of free space, μ = μrμ0, as stated above, is permeability, μr is relative permeability, μ0 is permeability of free space, the transverse mass of the electron is m/(1–β2)1/2, [7]. Increase of transverse mass of the electron is
is the velocity of the electron, ε = εrε0, as stated above is permittivity, εr is relative permittivity, ε0 is permittivity of free space, μ = μrμ0, as stated above, is permeability, μr is relative permeability, μ0 is permeability of free space, the transverse mass of the electron is m/(1–β2)1/2, [7]. Increase of transverse mass of the electron is
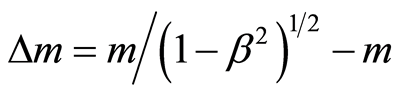 .
.
The kinetic energy of the electron, [6], is K = Dmc2, Figure 1. Using Equation (3) and noting that an electron holds an opposite charge to the nucleus, the potential energy of electron, [3,6], is
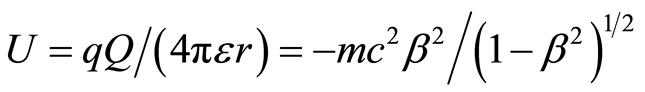 . The total mechanical energy of an electron, [6], is the sum of its kinetic and potential energies,
. The total mechanical energy of an electron, [6], is the sum of its kinetic and potential energies,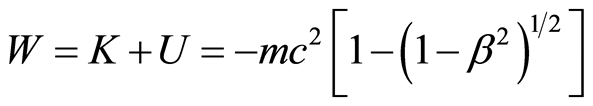 . According to the law of conservation of energy, this energy is equal to the negative emitted electromagnetic energy of the atom, Eem = –W = eV, where V is the potential difference through which the electron passes to get an equal energy as electromagnetic energy Eem. Out of the equation
. According to the law of conservation of energy, this energy is equal to the negative emitted electromagnetic energy of the atom, Eem = –W = eV, where V is the potential difference through which the electron passes to get an equal energy as electromagnetic energy Eem. Out of the equation  comes
comes 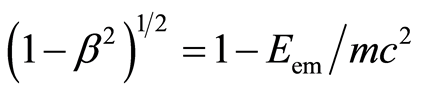 and
and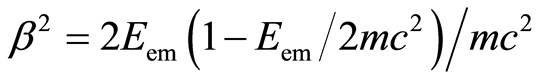 so the radius r in Equation (3) through arranging leads to:
so the radius r in Equation (3) through arranging leads to:
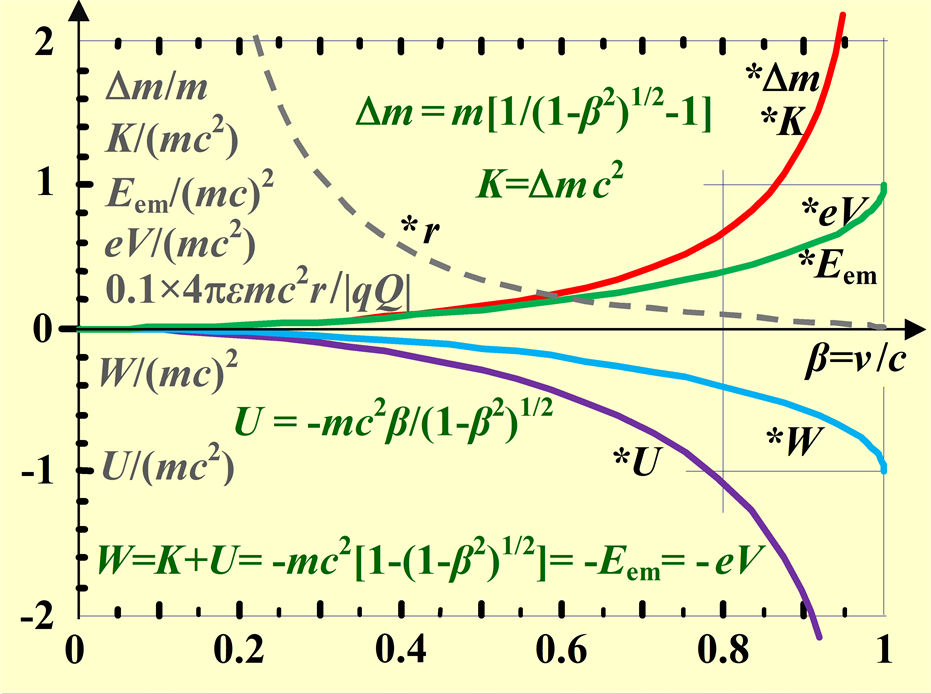
Figure 1. Energy relations in an atom (these relationships are valid for both classical and quantum physics; please note that the normalized quantities are marked with *). Radius of the circular orbit of the electron *r = r/[10|qQ|/(4pεmc2)], kinetic energy of the electron *K = K/(mc2), potential energy of the electron *U = U/(mc2), total mechanical energy of the electron *W = *K + *U, electromagnetic energy of the atom *Eem = –*W = *eV; all versus normalized velocity of the electron β = v/c.
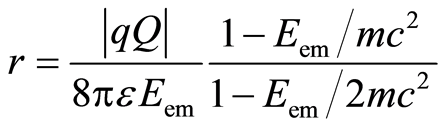 , (4)
, (4)
or
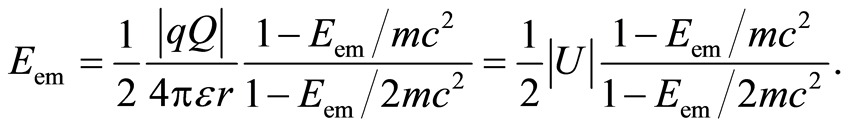 (5)
(5)
On the other hand, electromagnetic energy is , which means that Equation (5) we can write as:
, which means that Equation (5) we can write as:
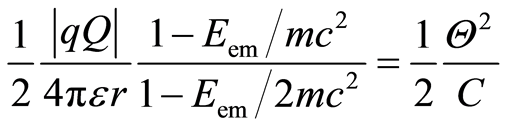 . (6)
. (6)
The single Equation (6) has two unknowns, i.e., parameter C and variable Θ. By using Diophantine equations we get one of the many solutions: C = 4πεr, and 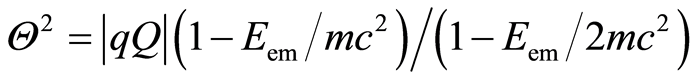 [8].
[8].
2.3. Natural Frequency of the Electromagnetic Wave in the Atom
Equation (6), which represents the electromagnetic energy in an atom, can be written like this [1]:
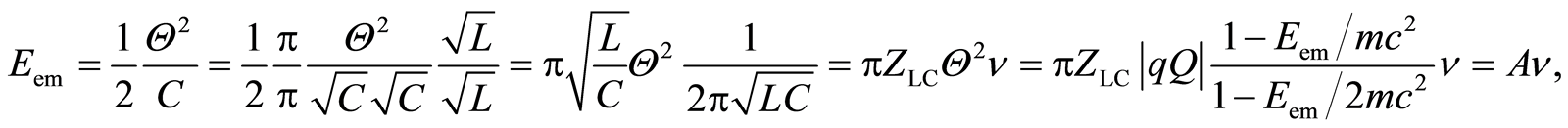 (7)
(7)
where
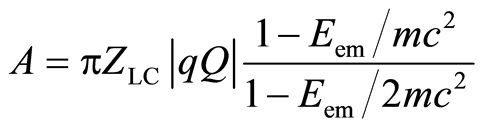 (8)
(8)
is the action of the electromagnetic oscillator, and
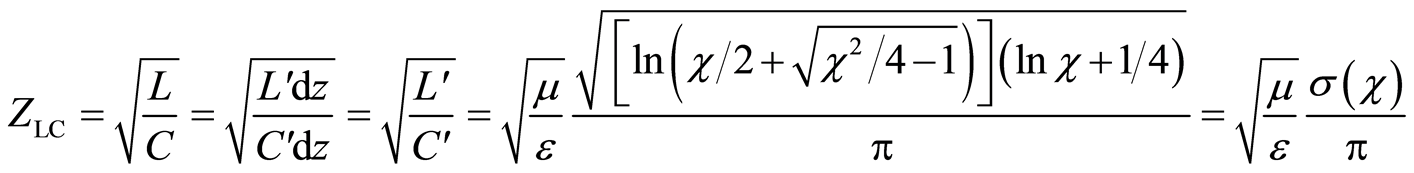 (9)
(9)
is the characteristic impedance of Lecher’s line, while
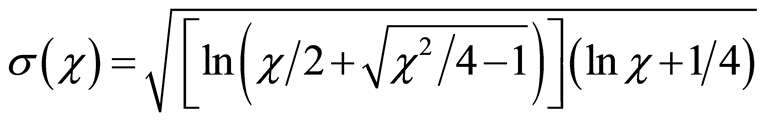 (10)
(10)
is the structural coefficient of Lecher’s line.
From Equation (7), in fact from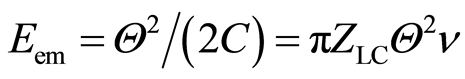 , furthermore from Equations (9) and C = 4πεr, follows the natural frequency of Lecher's line, i.e., follows the natural frequency of electromagnetic wave in an atom connected with an electron which is located on the orbit of radius r:
, furthermore from Equations (9) and C = 4πεr, follows the natural frequency of Lecher's line, i.e., follows the natural frequency of electromagnetic wave in an atom connected with an electron which is located on the orbit of radius r:
 . (11)
. (11)
Therefore in an atom with multiple electrons there are multiple natural frequencies ν. It should be noted that the same expression as (11) came from simultaneously multiplying and dividing the right side of the original expression  with
with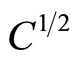 , and then using the expression C = 4πεr and Equation (9).
, and then using the expression C = 4πεr and Equation (9).
Equation (11) shows that the natural frequency ν does not depend on the amount of charge in the atom, but depends on the properties of the space (μ, ε), structural coefficient of Lecher's line σ(χ), (which for its part depends only on the parameters of Lecher's line d and r), and the radius r of the circular orbit. Indeed, electromagnetic oscillations in the atom require a charge, but amount of the charge does not affect the amount of the frequency ν.
If Equation (4) is inserted in Equation (11) we obtain natural frequency of electromagnetic wave in an atom:
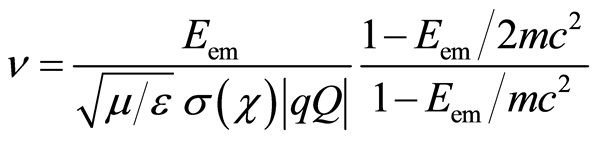 . (12)
. (12)
2.4. Structural Constant of the Atom
In the Equation (12) charges q and Q appear in the form of the product |qQ|. In order to satisfy the condition that the frequency ν is independent of the charge, and to avoid direct or indirect involvement of the charge, the total product 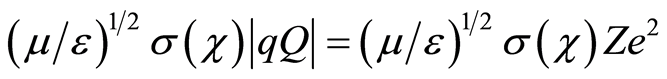 in Equation (12) must be a constant, i.e., only a product σ(χ)Z must be constant, because
in Equation (12) must be a constant, i.e., only a product σ(χ)Z must be constant, because 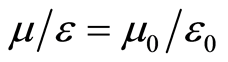 and e are already considered as constants. This product, in the form
and e are already considered as constants. This product, in the form
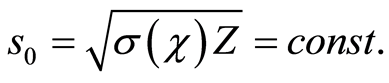 , (13)
, (13)
is called the structural constant of the atom. In the article [1] the value of structural constant has already been estimated (s0 = 8.277 56). However, the present paper shows accurate procedure for calculating this constant.
2.5. Action Constant of the Atom
From Equations (8), (9) and (13) follows
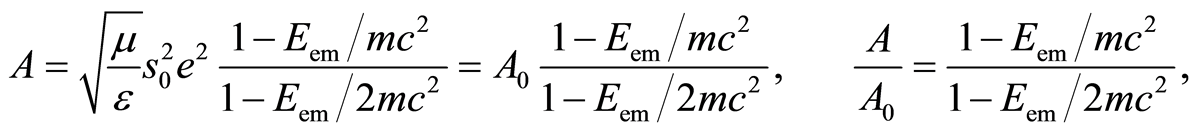 (14)
(14)
where
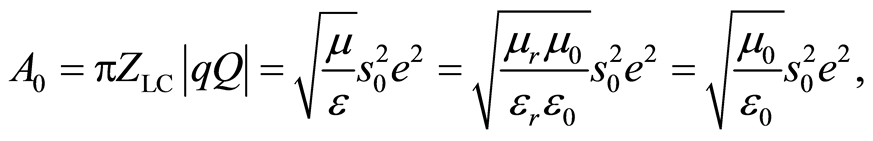 (15)
(15)
is action constant, which implies that μr = εr. Electromagnetic energy in Equation (7), i.e., Eem = Aν, using Equation (14), we can now write as:
 . (16)
. (16)
By solving this equation we obtain:
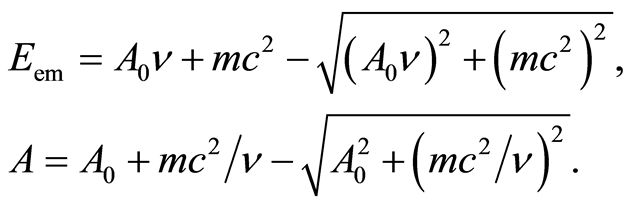 (17)
(17)
Taking into account that Eem = eV it is as follows:
 . (18)
. (18)
The extended Duane–Hunt's law we get from Equations (14) and (16) using Eem=eV [8], and using
 and
and 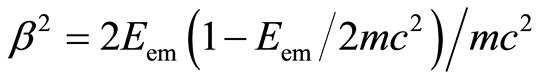 we get also a portion A0ν:
we get also a portion A0ν:
 (19)
(19)
From Equations (5) and (16) follows:
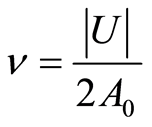 . (20)
. (20)
2.6. Phase Velocity of the Electromagnetic Wave in the Atom
Thanks to the analogy between the electromagnetic wave in the atom and the wave of voltage and current at the Lecher's line, according to Equations (1) and (2), and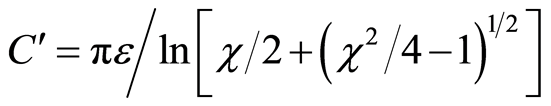 ,
, 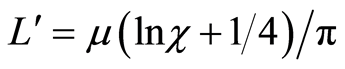 the phase velocity is, [3]:
the phase velocity is, [3]:
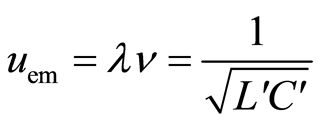 , (21)
, (21)
i.e., in normalized form [9]:
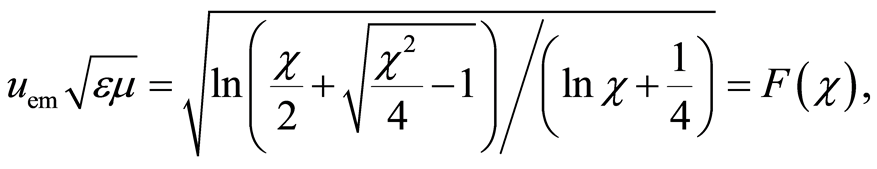 (22)
(22)
where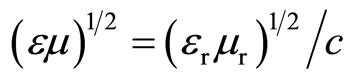 . In case
. In case 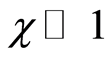 expression under the square root in Equation (22) then it is approximately equal to one as described in [1]. In this paper, however, we use the integral Equation (22) and analyze it in the area around χ=2, which is suitable for calculating the structural constant s0. Now we have a system of two equations with two unknowns, ε and μ,
expression under the square root in Equation (22) then it is approximately equal to one as described in [1]. In this paper, however, we use the integral Equation (22) and analyze it in the area around χ=2, which is suitable for calculating the structural constant s0. Now we have a system of two equations with two unknowns, ε and μ,
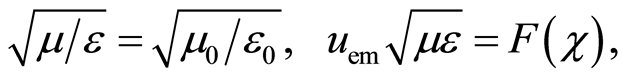 (23)
(23)
for which the solutions are (Figure 2):
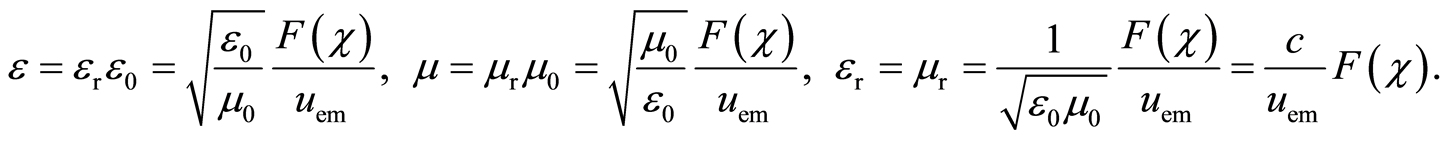 (24)
(24)
2.7. Wavelength and Momentum of Electromagnetic Wave in the Atom
The momentum of the electromagnetic wave in the atom is equal to the momentum of a photon [1], 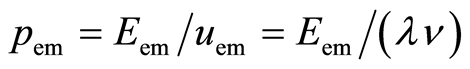 , Figure 2,
, Figure 2,
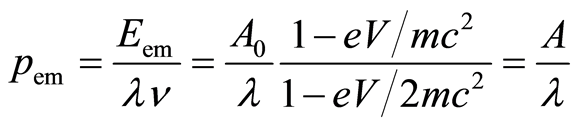 . (25)
. (25)
In accordance to the law of conservation of momentum, this momentum is equal to the linear momentum of the electron, [1],
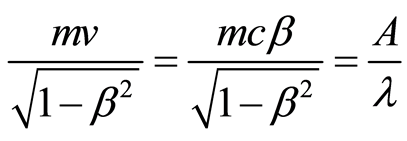 . (26)
. (26)
By applying the expressions 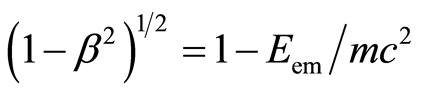 and
and 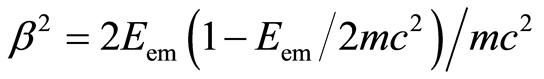 to Equation (26) we obtain
to Equation (26) we obtain
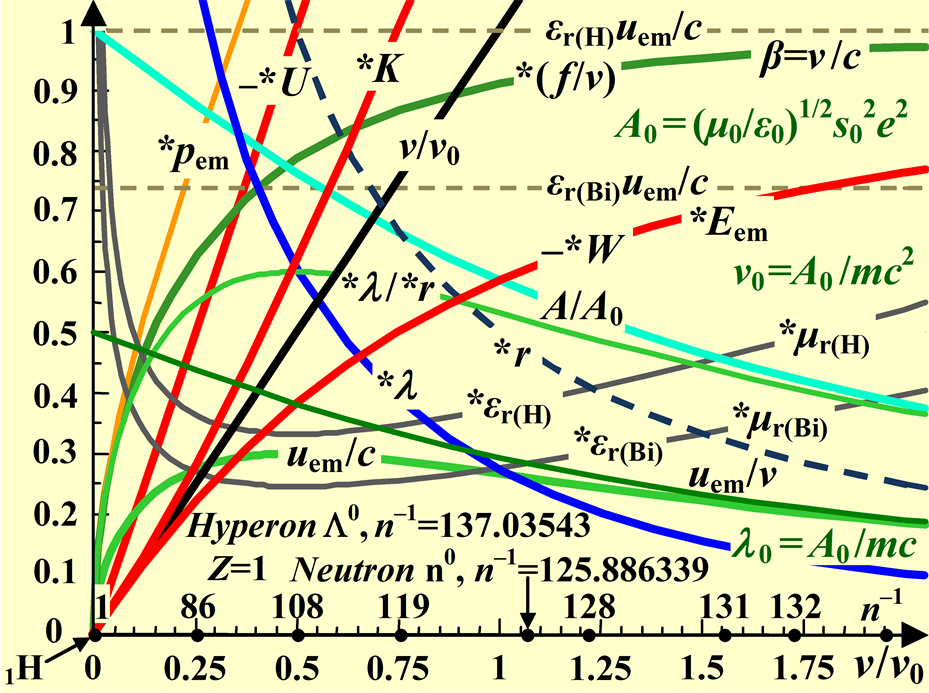
Figure 2. (Please note that the normalized quantities are marked with *). Radius of the circular orbit of the electron *r
= r/[|qQ|/(4pεmc2)], normalized velocity of the electron β = v/c, kinetic energy of the electron *K = K/(mc2), potential energy of the electron *U = U/(mc2), total mechanical energy of the electron *W = *K + *U, electromagnetic energy of the atom *Eem = –*W, momentum of electromagnetic wave in the atom *pem = pem/(mc), wavelength of the electromagnetic wave in the atom *l = l/[A0/(mc2)], normalized phase velocity of the electromagnetic wave in the atom uem/c and uem/v, normalized action of the electromagnetic oscillator A/A0, relative permittivity and relative permeability of the space in the hydrogen atom *εr(H) = *μr(H) = εr(H)/10 = μr(H)/10 and also relative permeability and relative permeability of the space within atom of bismuth *εr(Bi) = *μr(Bi) = εr(Bi)/10 = μr(Bi)/10, product of relative permittivity and normalized phase velocity εr(H)uem/c = μr(H)uem/c in the case of hydrogen, product of relative permittivity and normalized phase velocity εr(Bi)uem/c = μr(Bi)uem/c in the case of bismuth, the ratio of wavelength and radius *l/*r = (l/r)/(4pεcA0/|qQ|) = 2uem/c, the ratio of the frequency f of rotation of the electron orbiting atom and the frequency ν of the electromagnetic wave *(f/ν) = (f/ν)/(4εcA0/|qQ|), all versus normalized frequency of the electromagnetic wave in the atom ν/ν0, where ν0 = A0/mc2; n+1 = 1, 2, 3, … is ordinal number of stationary orbits in the atom, n–1 = 1/1, 1/2, 1/3, … 1/n, for hyperon X0 n–1 = 137.03587.
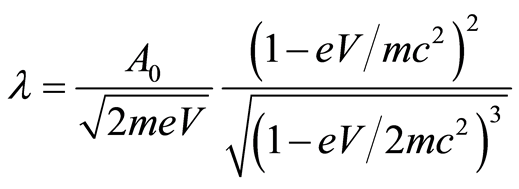 , (27)
, (27)
and using Equation (19) it becomes
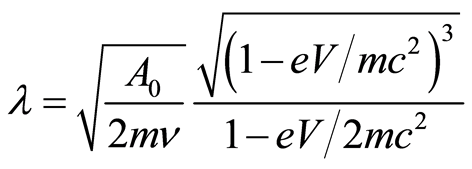 . (28)
. (28)
Phase velocity of the electromagnetic wave in an atom is obtained by multiplying Equations (19) and (27):
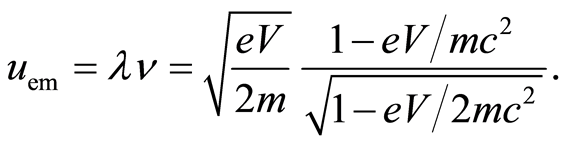 (29)
(29)
From (25) and (27) follows
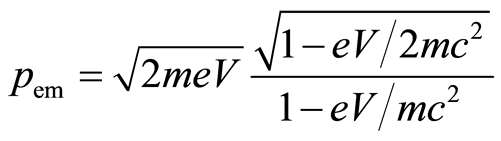 . (30)
. (30)
The ratio of the wavelength of the electromagnetic wave in the atom and the atom radius are obtained from Equations (4) and (27) using Eem=eV and Equation (29), Figure 2:
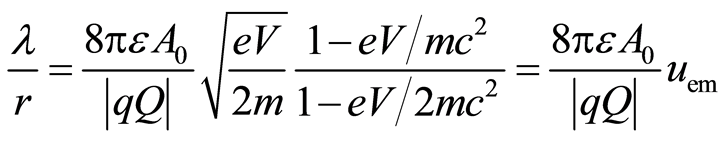 . (31)
. (31)
This expression, with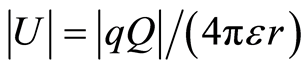 , leads to:
, leads to:
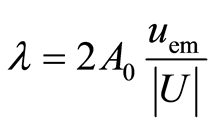 . (32)
. (32)
A minimum of two separate oscillating processes are performed simultaneously within an atom, i.e., the circular motion of electrons around the nucleus and oscillation of electromagnetic wave energy [10]. The time period of one circular tour of electrons around the nucleus is Te = 2rp/v = 1/f, where f is the frequency of circulation of electrons around the nucleus. The duration of the period of the electromagnetic wave is Tem = 1/ν. Hence, ν/f = 2pνr/v. Using Equation (31), as well as v/c = β and lν = uem follows, Figure 2:
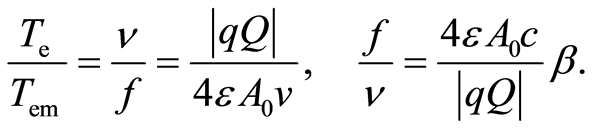 (33)
(33)
2.8. Stationary States of the Atoms
Long term existence of the rotation of electrons and long term existence of the electromagnetic wave in the atom (stationary state) is only possible if there is synchronism between them (synchronously stationary state) [10,11]. To be coherent with the active power of the electromagnetic wave in an atom, the electron needs to oscillate (i.e., rotate) with dual frequency of the wave, because the active power of wave oscillates with dual frequency 2w = 2(2pν), (this will be further discussed in Sub–Heading 2.9). This means that in the synchronously stationary state of the atom, the time period of electron rotation Te is a half period of Tem (or, for reasons of synchronism, is n±1-multiple of a half period of Tem), i.e., Te = n±1Tem/2, where n = 1, 2, 3, … is ordinal number of stationary orbits in the atom (or n–1 = 1/1, 1/2, 1/3, … 1/n). Equation (33) gives the speed of electron in a synchronously stationary state ([11], compare with [6]):
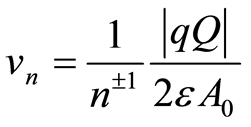 . (34)
. (34)
The Equations (3) and (34) give the radius of the electron orbits in the synchronously stationary states:
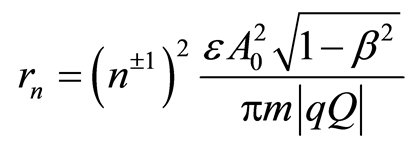 . (35)
. (35)
From Equations (33), (34) and (35) follows [11]:
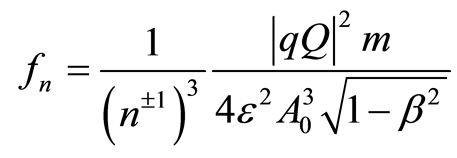 , (36)
, (36)
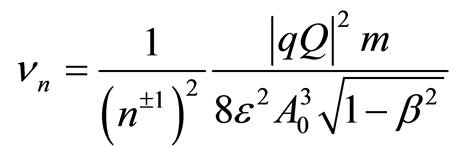 , (37)
, (37)
and, [10],
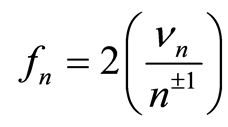 . (38)
. (38)
The total mechanical energy of an electron Wn= –Eem(n) follows from Equations (17) and (37):
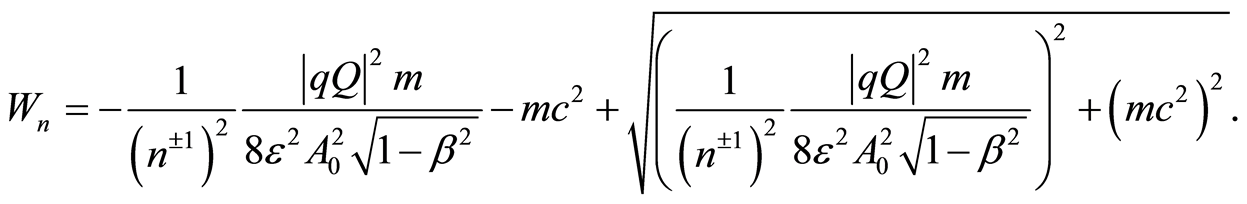 (39)
(39)
For energies much smaller than mc2:
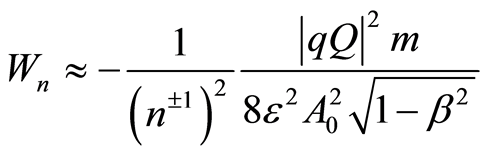 . (40)
. (40)
If assume the maximum speed of electron is equal to the speed of light in a given medium, i.e., according to Equation (22) vmax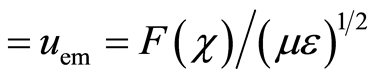 (to increase the speed of electron should be n±1 = 1/nmax) from Equations (15) and (34) we get:
(to increase the speed of electron should be n±1 = 1/nmax) from Equations (15) and (34) we get:
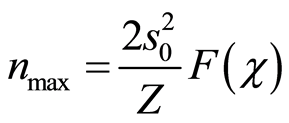 . (41)
. (41)
From Equation (41) follows the greatest possible atomic number Zmax when nmax is minimal and 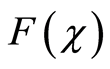 is maximal, really when nmax = 1 and
is maximal, really when nmax = 1 and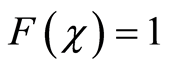 , i.e.,
, i.e.,
 . (42)
. (42)
2.9. Wave Equations of the Electromagnetic Wave in the Atom
Wave equations of electromagnetic wave in an atom are expressed by Equation (1). If we insert phase velocity uem in these equation from Equation (29), i.e.,
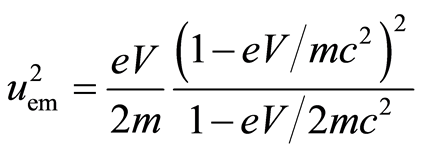 , (43)
, (43)
we obtain
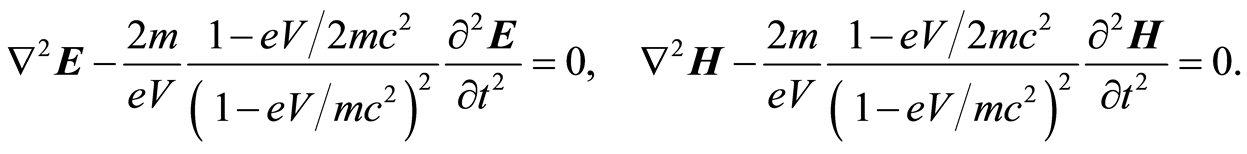 (44)
(44)
Wave equations (1) and (44) have a lot of solutions. We will apply the solutions that correspond to the transmission line, i.e., to the LC network. These solutions are standing waves [12,13]:
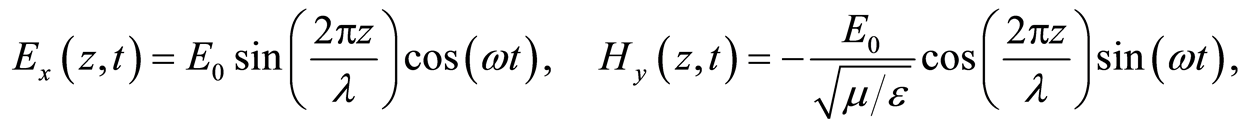 (45)
(45)
where E0 is the maximum value, i.e., the amplitude of electric field strength E, Ex(z,t) is the x-component of the electric field strength dependent on the z-axis and the time t, and Hy(z,t) is the y-component of the magnetic field strength H dependent on the z-axis and the time t, w = 2pν. All mathematical operations we perform for the y-component of the magnetic field Hy(z,t) can be performed for the x-component of the electric field Ex(z,t) in the same way.
In the standing waves (45) the energy oscillates between the electric and magnetic form. The electrical energy is maximum when the magnetic energy is zero, and vice versa. Furthermore, the standing wave transfers no energy through the space because the average active power of the wave is equal to zero. The current value of the active power oscillates in both directions, + and – of z axis, with dual frequency 2w from point to point of z axis [12]. As already mentioned, this is why (for the maintenance of stationary state of the atom) the electron has to rotate twice as fast compared to the lower harmonics (n+1), or twice as fast compared to the upper harmonics (n–1), i.e., f = 2(ν/n±1) in accordance with Equation (38).
If we use the second derivative with respect to z of the y-component Hy(z,t) of the magnetic field strength in Equation (45), we get: ¶2Hy(z,t)/¶z2 + (2p/l)2Hy(z,t) = 0. After inclusion of the wavelength l from Equation (27) we obtain:
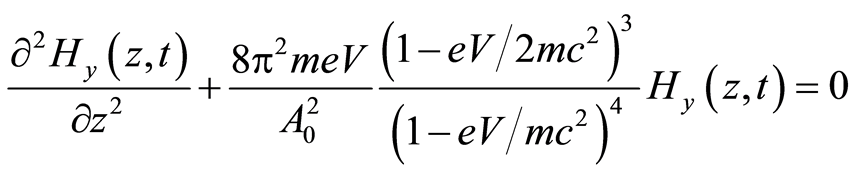 , (46)
, (46)
If eV/mc2 << 1, then eV » K = W – U, and Equation (46) becomes
 (47)
(47)
The second derivative of Hy(z,t) with respect to t gives:
¶2Hy(z,t)/¶t2 + w2Hy(z,t) = 0. After inclusion of the angular frequency w = 2pν from Equation (19) we obtain:
 . (48)
. (48)
If eV/mc2 << 1, then eV » K = W – U, and equation (48) becomes
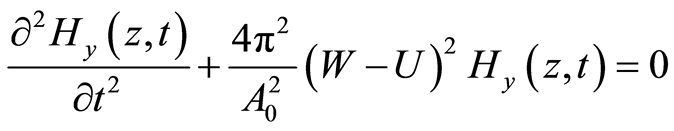 . (49)
. (49)
3. Calculation of the Structural Constant s0
Structural constant of the atom s0 can be determined in several ways, e.g., by measuring two quantities, the voltage V and frequency ν and calculating the action constant A0 by Duane–Hunt’s law, i.e., using Equations (15) and (19), [8]. However, here we will use a more direct theoretical calculation, with only one empirical item necessary.
Namely, the increase of the nuclear charge in the atom increases atomic number Z. In accordance with Equation (13), the value of structural coefficient σ(χ) = s02/Z is assigned to each atom. So, greater atomic number means a lower structural coefficient σ(χ).
On the other hand, there is a critical nuclear charge which ensures stability of the atom [2,14]. In other words, to reduce σ(χ) means to grow instability of the atom. In general, the higher atomic number means the less stability (i.e., the less half–life, or t1/2) of the atom, starting from bismuth 83Bi (Z = 83, t1/2 = 6 × 1026 s, [15]) to ununoctium 118Uuo (Z = 118, t1/2 = 5 ms), [exceptions are atoms of technetium (43Tc, Z = 43, t1/2 = 1.3 × 1014 s) and promethium (63Pm, Z = 63, t1/2 = 5.6 × 108 s)].
For the calculation of structural constant s0, it is enough to find only one associated pair of σ(χ) and Z. The curve σ(χ) has no extremes, Figure 3. Thus it is not easy to find a mentioned pair of σ(χ) and Z. In that sense, a better situation is with the phase velocity uem, specifically with the normalized phase velocity uem(με)1/2 = F(χ) of electromagnetic wave in the atom, Figure 3, [9]. Neither of these two curves have extremes, but there is a sharp knee on F(χ) which can be used to determine the structural constant s0.
Although there is no theory about the connection between the phase velocity of electromagnetic waves in the atom and the stability of the atoms, it is still possible to use this mathematical benefit of sharp knee for those atoms, in which there is the lower phase velocity of electromagnetic waves that exhibit greater instability. Use of this result will be discussed just a little bit later.
The nuclear binding energy per nucleon slightly decreases with increase the atomic number (starting from the first radioactive element bismuth, 83Bi, 7.848 MeV, to the unoctium, 118Uuo, 7.074 MeV, about 0.31% decrease for each 35 atoms in that area [15]). Physically this means that the boundary between stable and unstable areas is not emphasized. Mathematically it allows that between the two areas set up so–called transition area, Figure 3. This is, at the moment, the most accurate way to determine the boundary between stable atoms and the others. Indeed, the first unstable atom must be located on that border. This is a key fact to determine the structural constant s0 of the atom.
Before calculating, we observe the first derivative F'(χ) of the curves of normalized phase velocity F(χ) of electromagnetic waves in an atom (Figure 3). When this derivative is greater than 1, it means that the phase velocity rapidly decline, it is a zone of unstable atoms (2 < χ < 2.129 531 7). It should be noted that the situation χ ≤ 2 is theoretically impossible because then there is no Lecher's line.
When the second derivative F''(χ) of the normalized phase velocity F(χ) is greater than 1, it means that the phase velocity starts to rapidly decline (Figure 3), this is a transition zone (2.129 531 7 < χ < 2.382 788).
The border crossing from the transition zone to the stable zone (i.e., χ0 = 2.382 788), in accordance with the experiments, [15], is closest to the bismuth atom. Bismuth atom (83Bi) is the first unstable atom, in the entire chain of stable atoms, which ends with lead (82Pb). The corresponding value of the structural coefficient in that place is σ(χ0) = 0.825 402, Figure 3. Bismuth is a chemical element with atomic number Z = 83, with half–life more than a billion times the estimated age of the universe. Even though charges in reality take discrete values (e, 2e, 3e, … Ze), theoretical value of Z in Equation (13) can be within the range Zth = 83 ± 1/2. Thus, according to Equation (13) we get the structural constant of the atom [0.825 402 × (83 ± 1/2)]1/2, i.e., 8.252 < s0 < 8.302, with a mean value 8.277 and with sample standard deviation ±0.035 355 or as a percentage s0 = 8.277 ± 0.43%.
4. Conclusion
In classical physics, the use of Maxwell’s equations and Lorentz theory of electrons gives us equations that describe the behavior of atom. For this description, usual classical physical constants are sufficient. The only new necessary physical constant is the structural constant of the atom s0. This new physical constant was calculated in the framework of a unified theory based on the model of the atom by analogy with the transmission line. To
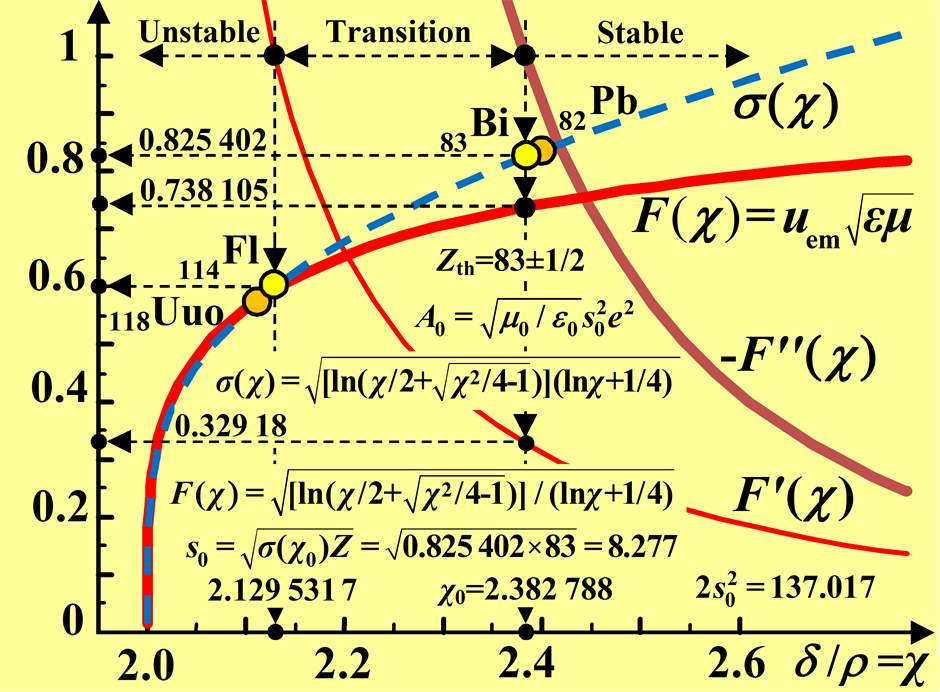
Figure 3. Structural coefficient of Lecher's line σ(χ), normalized phase velocity of the electromagnetic wave in the atom F(χ) = uem(με)1/2, the first derivative of the normalized phase velocity F' (χ), inverted second derivative of the normalized phase velocity F''(χ), all versus ratio δ/ρ = χ of the transmission Lecher’s line, consisting of a pair of ideal conducting nonmagnetic parallel wires of radius ρ separated by δ, which represents a model of an atom.
calculate it, we need only one empirical item, i.e., the atomic number of the first unstable atom in periodic table of elements. It is known, that it is bismuth, with atomic number Z = 83. From this data, the structural constant s0 is calculated. Thus, we get s0 = 8.277 ± 0.43%. Comparing with the fine structure constant we get s0 = 8.27756, which is consistent with the calculation performed here (the relative difference is less than 0.0068%). This constant, thanks to the expressions (μ0/ε0)1/2s02e2 and (2s02)–1, can replace two existing constants, Planck’s constant h and the fine structure constant α. We get also the stationary states of the atoms and the maximal atomic number Z = 2s02 = 137.036, i.e., as integer should be Zmax = 137. The difference between 2s02 and Zmax we call the slipping. This indicates that, in addition to integer synchronously stationary states, non-integer (asynchronously) stationary states in atoms are also possible. Now, just a mention, as it seems to asynchronously stationary states can produce a continuous spectrum of atoms. This, however, requires more detailed research. This model of the atoms covers the energies of the electromagnetic, weak and strong fundamental interactions [16].
Acknowledgements
Wolfram Research, Inc. Mathematica software is used by courtesy of Systemcom Ltd., Zagreb, Croatia. The author thanks Ms. Erica Vesic for editing this article in English, Mr. Damir Vuk for the useful discussions and Prvomajska TZR Ltd., Zagreb, Croatia, www.prvomajska-tzr.hr, for the financial support.
REFERENCES
[1] M. Perkovac, “Model of an Atom by Analogy with the Transmission Line,” Journal of Modern Physics, Vol. 4, No. 7, 2013, pp. 899-903. http://dx.doi.org/10.4236/jmp.2013.47121.
[2] H. Hänsel and W. Neumann, “Physik,” Spektrum Akademischer Verlag, Heidelberg, 1995.
[3] Czichos and Association Hütte, “Die Grundlagen der Ingenieurwissenschaften,” Springer-Verlag, Berlin, 1989.
[4] T. Bosanac, “Teoretska elektrotehnika 1,”Tehnicka knjiga, Zagreb, 1973.
[5] R. Rüdenberg, “Elektrische Schaltvorgänge,” Julius Springer, Berlin, 1923.
[6] D. C. Giancolli, “Physics for Scientists and Engineers,” Prentice Hall, Englewood Cliffs, 1988.
[7] L. Page and N. I. Adams, “Electrodynamics,” D. Van Nostrand Company, Inc., New York, 1940.
[8] M. Perkovac, “Statistical Test of Duane—Hunt’s Law and Its Comparison with an Alternative Law,” 2010. http://arxiv.org/abs/1010.6083.
[9] M. Perkovac, “Maxwell Equations for Nanotechnology,” Proceedings of the 35th International Convention of the IEEE MIPRO, Opatija, 21-25 May 2012, pp. 429-436. http://ieeexplore.ieee.org/xpl/freeabs_all.jsp?arnumber=6240683.
[10] M. Perkovac, “Quantization in Classical Electrodynamics,” Physics Essays, Vol. 15, No. 1, 2002, pp. 41-60. http://dx.doi.org/10.4006/1.3025509.
[11] M. Perkovac, “Absorption and Emission of Radiation by an Atomic Oscillator,” Physics Essays, Vol. 16, 2003, pp. 162-173. http://dx.doi.org/10.4006/1.3025572.
[12] Z. Haznadar and Z. Stih, “Elektromagnetizam,” Skolska knjiga, Zagreb, 1997.
[13] J. D. Jackson, “Classical Electrodynamics,” John Wiley & Sons, Inc., New York, 1999.
[14] R. D. Benguria, M. Loss and H. Siedentop, “Stability of Atoms and Molecules in an Ultrarelativistic Thomas-FermiWeizsäcker Model,” Journal of Mathematical Physics, Vol. 49, 2007, Article ID: 012302. http://dx.doi.org/10.1063/1.2832620.
[15] http://periodictable.com/Isotopes/001.1/index.html.
[16] http://www.physics.upenn.edu/~pgl/e27/E27.pdf.
NOTES

*Corresponding author.

